Theory Meeting, Nov. 14th

[Lyle Kopnicky]

We'll discuss Chapter 17, "The Natural Numbers and Induction", of Logic and Proof (https://leanprover.github.io/logic_and_proof/). Please read the material beforehand and try your hand at the exercises. At the meeting anyone will be able to present and contribute to the discussion.

November 14th, 2018, 6:30-8:30pm

Location:

Collective Agency

3050 SE Division, Suite 245 · Portland, OR

We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.

RSVP at:

https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/gwtbcpyxpbsb/

[Lyle Kopnicky]

Another meeting full of interesting discussions.

I’ve attached a PDF with Ed’s answer to Exercise 17.2.

Here’s my answer to Exercise 17.1:

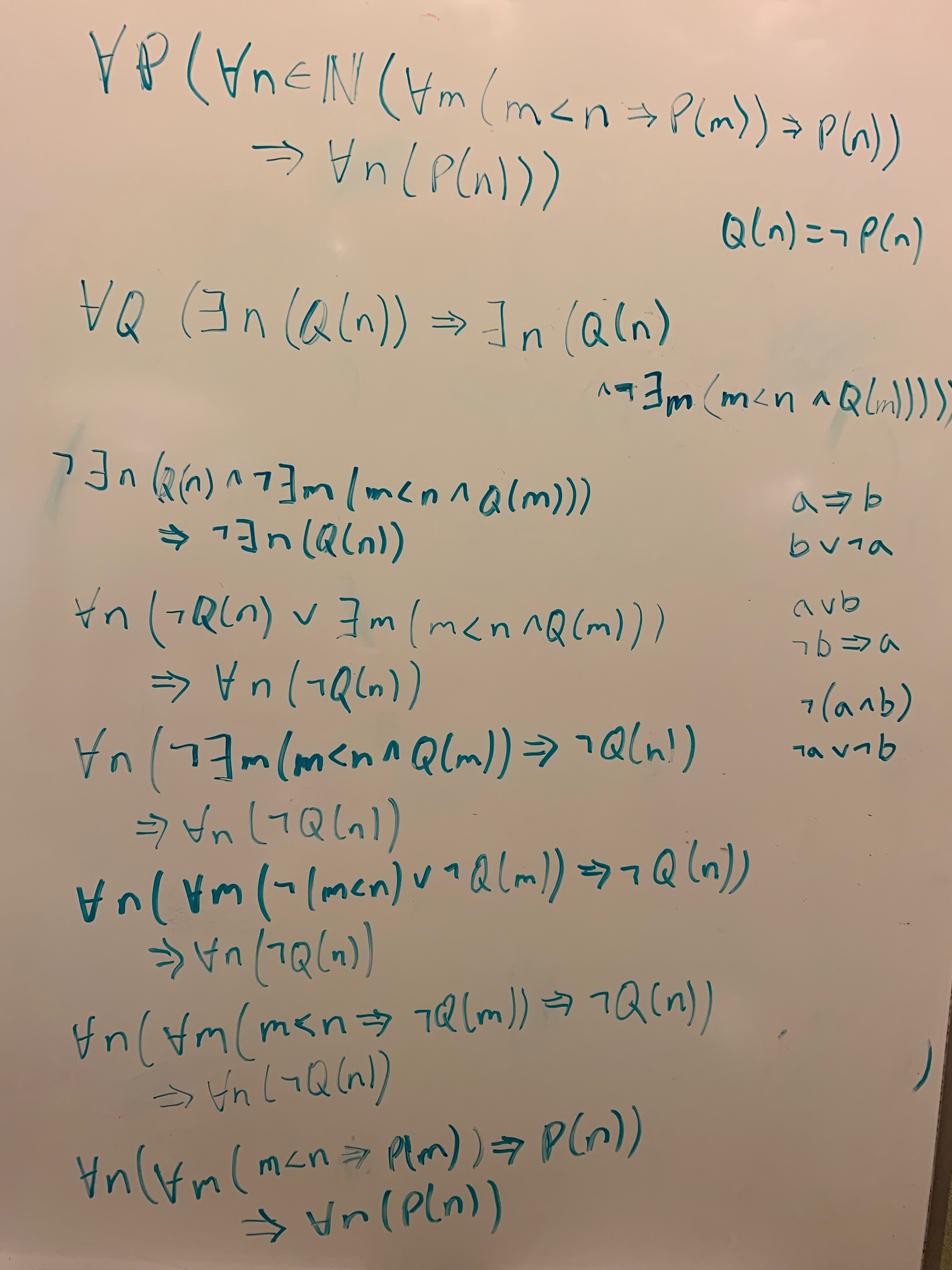
…and here’s the sketch of a proof for Exercise 17.19 that we worked out in the meeting:

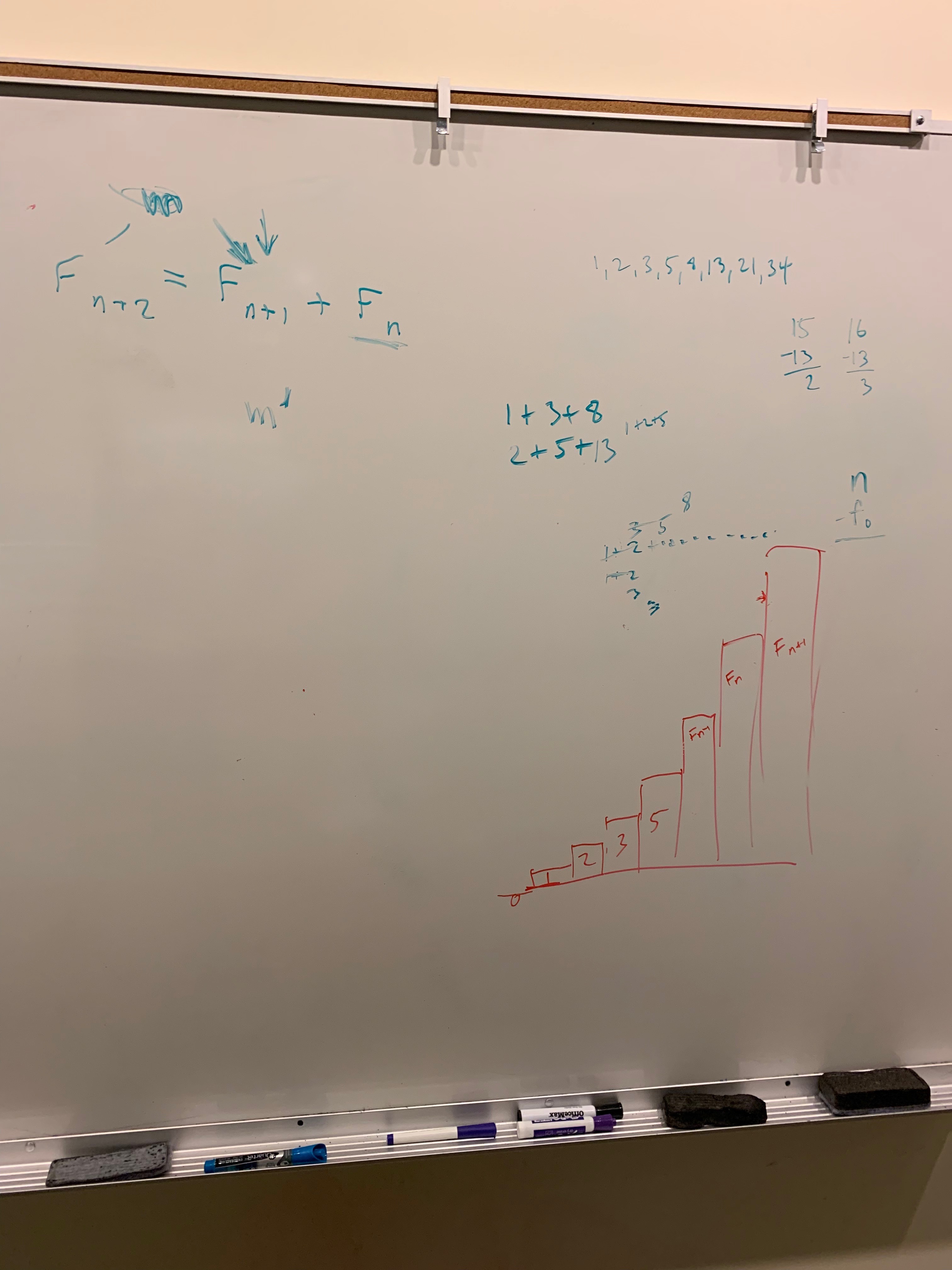
The objective of that exercise was to prove that every natural number can be expressed as the sum of non-consecutive Fibonacci numbers. As a reminder, each Fibonacci number is defined as the sum of the two previous Fibonacci numbers:  , , and . Thus the sequence begins with 0, 1, 1, 2, 3, 5, 8, 13, 21.

We had to clarify a bit what's meant by non-consecutive. The insight here is that the result is a set of Fibonacci numbers, rather than a set of indices of Fibonacci numbers. Thus, 1 is not considered consecutive to itself, nor can 1 be considered non-consecutive to 2 because there is a 1 inbetween.

We proceed using complete induction (aka strong induction), proving the result for  assuming that it holds for all natural numbers less than . The first step is to find the greatest Fibonacci number less than or equal to . Let's call it . If it's equal to , we're done. If it's less than , we then need to find our set of non-consecutive Fibonacci numbers less than or equal to the remainder, . Well, we know by our induction hypothesis that such a set exists. However, might it be the case that the greatest Fibonacci number in the that set is consecutive to ? That is, could it be ?

Here's where the definition of the Fibonacci sequence comes in handy. It turns out that each Fibonacci number is less than twice the prior one. Since we know that , and , subtracting from each part of the inequality, we have that . Since the remainder we're looking for is smaller than , the set that sums to it can't include . Thus we have satisfied the non-consecutive property.

Here's a Haskell program I wrote to find an increasing list of Fibonacci numbers that sum to the supplied natural number: https://gist.github.com/lylek/24caa515d757a89b9a7ce369fa4df390.

Sample output for 0-20:

[0]

[1]

[2]

[3]

[1,3]

[5]

[1,5]

[2,5]

[8]

[1,8]

[2,8]

[3,8]

[1,3,8]

[13]

[1,13]

[2,13]

[3,13]

[1,3,13]

[5,13]

[1,5,13]

[2,5,13]

--
You received this message because you are subscribed to the Google Groups "pdxfunc" group.
To unsubscribe from this group and stop receiving emails from it, send an email to pdxfunc+u...@googlegroups.com.
To post to this group, send email to pdx...@googlegroups.com.
Visit this group at https://groups.google.com/group/pdxfunc.
For more options, visit https://groups.google.com/d/optout.

[Lyle Kopnicky]

BTW, although the time to produce the list of Fibonacci numbers summing to the given number is linear in the given number, the time to calculate the sequence of lists summing to each of 0-n is quadratic in n. If this is the desired use case, one could speed it up by memoizing fibsSummingTo for the target value, similarly to the way that the list of Fibonacci numbers itself is cached in fibs.

[Lyle Kopnicky]

My mistake - it's not linear in the target number. It's linear in the number of Fibonacci numbers less than the target number. Since the Fibonacci sequence is exponential, that means it runs in time approximately proportional to the log of the target number!

I'm hand-waving a bit over the size of the numbers themselves, as each takes space proportional to log(n), with the subtraction operation taking similar time.

But it's basically instant, no matter how big I make the target number. Well, at least up to 10 ^ 10000, it took under a second. For 10 ^ 100000, it took about 12 seconds. And the vast majority of that time was calculating the Fibonacci number sequence itself, not finding the numbers that sum to the total.