Theory meeting, Jan. 9th

9 views

Skip to first unread message

Lyle Kopnicky

unread,

Dec 28, 2018, 11:30:35 AM12/28/18

to pdxfunc

We'll discuss Chapter 19, "Elementary Number Theory", of Logic and Proof (https://leanprover.github.io/logic_and_proof). Please try to work the exercises beforehand. At the meeting anyone will be able to present and contribute to the discussion.

January 9th, 2018, 6:30-8:30pm

Location:

Collective Agency

3050 SE Division, Suite 245 · Portland, OR

We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.

RSVP at:

https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/gwtbcpyzcbmb/

Lyle Kopnicky

unread,

Dec 28, 2018, 3:16:59 PM12/28/18

to pdxfunc

I read Chapter 19, and found three errors in it.

The first is in Section 19.2, in the proof of $\mathrm{gcd}(n, m) = \mathrm{gcd}(m, n-km).$ They define $d = \mathrm{gcd}(n, m)$ and $r = n -km$ . Then they say that if $n = m = 0$ , that $d = 0 = \mathrm{gcd}(m, r)$ . That's not correct. It should say $d = 1 = \mathrm{gcd}(m, r)$ . This is because, $\mathrm{gcd}(0, 0) = 1$ . The proof still follows from that. Note that the integer $0$ can never be the greatest common divisor of two integers, because $1$ divides every integer, and it's greater than $0$ .

The second is in Section 19.4, where they claim "there are only four possibilities for $a^2 + b^2\ (\mathrm{mod}\ 4)$ . It can be congruent to $0 + 0$ , $1 + 0$ , $0 + 1$ or $0 + 0$ ." They missed the possibility that both $a^2$ and $b^2$ are congruent to $1$ modulo $4$ . Then the sum would be congruent to $2$ modulo $4$ . That still isn't $3$ , so the proof is safe, but the step should be corrected.

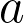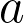The third is also in Section 19.4, in the proof that $a$ has a multiplicative inverse modulo $n$ only if $n$ and $a$ are coprime. They define $d = \mathrm{gcd}(a, b)$ , but it should say $d = \mathrm{gcd}(a, n)$ . That took me a while to figure out. What didn't make sense to me was how they justified $d\ |\ n$ .

I also noticed a missing period, and a place where they began a sentence with a variable, which isn't good editorial practice.

There's also a place that may not have an error, but I couldn't follow a step: In the proof of the Fundamental Theorem of Arithmetic, in section 19.3. Specifically, where it says "Since $p_k$ is prime, we must have $p_k\ |\ q_j$ for some $j \le l$ ." I'm not sure how that follows. Perhaps we can discuss in the meeting.

- Lyle

--
You received this message because you are subscribed to the Google Groups "pdxfunc" group.
To unsubscribe from this group and stop receiving emails from it, send an email to pdxfunc+u...@googlegroups.com.
To post to this group, send email to pdx...@googlegroups.com.
Visit this group at https://groups.google.com/group/pdxfunc.
For more options, visit https://groups.google.com/d/optout.

Lyle Kopnicky

unread,

Dec 28, 2018, 4:34:37 PM12/28/18

to pdxfunc

Hmm, regarding the first error: Looks like it's intentional. Above that in the book it says that they define $\mathrm{gcd}(0, 0) = 0$ . I'm not sure why they would need to define that special case, or define it that way. It already follows from the standard definition that $1$ divides $0$ , thus $\mathrm{gcd}(0, 0) = 1$ . I don't understand why they would want to special-case that.

Lyle Kopnicky

unread,

Dec 28, 2018, 4:50:14 PM12/28/18

to pdxfunc

Oh, I see. Because every integer is a divisor of $0$ , there is no greatest. So you either have to say it's undefined, or pick something useful.

For any nonzero $n$ , we have $\mathrm{gcd}(n, n) = n$ . So if we define $\mathrm{gcd}(0, 0)$ to be $0$ , then that holds for $n = 0$ as well.

Which makes it handy, as Wikipedia points out, in defining a lattice of the natural numbers with "divides" as the relation: since gcd is the meet operation, that gives the lattice a bottom.

Lyle Kopnicky

unread,

Dec 31, 2018, 8:11:11 PM12/31/18

to pdxfunc

I’ve attached my solutions to the exercises.

Also, I have an even better justification for the definition of $\gcd(0, 0) = 0$ . It's not an exceptional case at all. You just have to rethink what "greatest" means. Rather than thinking "greatest" in terms of the usual ordering on integers, think of it in terms of the divisibility relation. Zero is the greatest number in that relation, because every integer divides it.

Another way to look at it is that for the greatest common divisor, we require two things: 1) that $\gcd(n, m)$ divides both $n$ and $m$ , and 2) that any integer that divides both $n$ and $m$ divides $\gcd(n, m)$ . In lattice theory, this is called the infimum or meet. What are the divisors of zero? All integers. But only one of those integers is a multiple of all the others: zero.

I also found a couple of mistakes in the exercises:

Exercise 6: Write 11160 as product of primes.

Should be: Write 11160 as the product of primes.

Exercise 19: Suppose that a | n and a | n

Should be: Suppose that a | n and a | m

Also on Exercise 19, it seems they should require that $n$ and $m$ cannot both be zero. Which also turns out to prevent 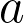$a$ and $d$ from being zero.

ch19-exercises.pdf

Lyle Kopnicky

unread,

Jan 16, 2019, 6:47:13 PM1/16/19

to pdxfunc

We had a great discussion. Everyone had a chance to show some of their solutions.

BTW, a note regarding the below: You can't always think of "greatest" in terms of the divisibility relation. For example, what's the gcd of 4 and 6? It could be 2 or -2: which is greater? In terms of the divisibility relation, each divides the other: neither is greater. So you have to resort to the usual ordering on the integers to pick 2.

On Monday, December 31, 2018 at 8:11:11 PM UTC-5, Lyle Kopnicky wrote:

I’ve attached my solutions to the exercises.

Also, I have an even better justification for the definition of $\gcd(0, 0) = 0$ . It's not an exceptional case at all. You just have to rethink what "greatest" means. Rather than thinking "greatest" in terms of the usual ordering on integers, think of it in terms of the divisibility relation. Zero is the greatest number in that relation, because every integer divides it.

Another way to look at it is that for the greatest common divisor, we require two things: 1) that $\gcd(n, m)$ divides both and , and 2) that any integer that divides both and divides $\gcd(n, m)$ . In lattice theory, this is called the infimum or meet. What are the divisors of zero? All integers. But only one of those integers is a multiple of all the others: zero.

I also found a couple of mistakes in the exercises:

Exercise 6: Write 11160 as product of primes.
Should be: Write 11160 as the product of primes.

Exercise 19: Suppose that a | n and a | n
Should be: Suppose that a | n and a | m

Also on Exercise 19, it seems they should require that and cannot both be zero. Which also turns out to prevent and from being zero.

On Fri, Dec 28, 2018 at 4:50 PM Lyle Kopnicky wrote:

Oh, I see. Because every integer is a divisor of , there is no greatest. So you either have to say it's undefined, or pick something useful.

For any nonzero , we have $\mathrm{gcd}(n, n) = n$ . So if we define $\mathrm{gcd}(0, 0)$ to be , then that holds for as well.

Which makes it handy, as Wikipedia points out, in defining a lattice of the natural numbers with "divides" as the relation: since gcd is the meet operation, that gives the lattice a bottom.

On Fri, Dec 28, 2018 at 4:34 PM Lyle Kopnicky wrote:

Hmm, regarding the first error: Looks like it's intentional. Above that in the book it says that they define $\mathrm{gcd}(0, 0) = 0$ . I'm not sure why they would need to define that special case, or define it that way. It already follows from the standard definition that divides , thus $\mathrm{gcd}(0, 0) = 1$ . I don't understand why they would want to special-case that.

On Fri, Dec 28, 2018 at 3:16 PM Lyle Kopnicky wrote:

I read Chapter 19, and found three errors in it.

The first is in Section 19.2, in the proof of $\mathrm{gcd}(n, m) = \mathrm{gcd}(m, n-km).$ They define $d = \mathrm{gcd}(n, m)$ and . Then they say that if , that $d = 0 = \mathrm{gcd}(m, r)$ . That's not correct. It should say $d = 1 = \mathrm{gcd}(m, r)$ . This is because, $\mathrm{gcd}(0, 0) = 1$ . The proof still follows from that. Note that the integer can never be the greatest common divisor of two integers, because divides every integer, and it's greater than .

The second is in Section 19.4, where they claim "there are only four possibilities for $a^2 + b^2\ (\mathrm{mod}\ 4)$ . It can be congruent to , , or ." They missed the possibility that both and are congruent to modulo . Then the sum would be congruent to modulo . That still isn't , so the proof is safe, but the step should be corrected.

The third is also in Section 19.4, in the proof that has a multiplicative inverse modulo only if and are coprime. They define $d = \mathrm{gcd}(a, b)$ , but it should say $d = \mathrm{gcd}(a, n)$ . That took me a while to figure out. What didn't make sense to me was how they justified $d\ |\ n$ .

I also noticed a missing period, and a place where they began a sentence with a variable, which isn't good editorial practice.

There's also a place that may not have an error, but I couldn't follow a step: In the proof of the Fundamental Theorem of Arithmetic, in section 19.3. Specifically, where it says "Since is prime, we must have $p_k\ |\ q_j$ for some $j \le l$ ." I'm not sure how that follows. Perhaps we can discuss in the meeting.

- Lyle

On Fri, Dec 28, 2018 at 11:30 AM Lyle Kopnicky wrote:

We'll discuss Chapter 19, "Elementary Number Theory", of Logic and Proof (https://leanprover.github.io/logic_and_proof). Please try to work the exercises beforehand. At the meeting anyone will be able to present and contribute to the discussion.

January 9th, 2018, 6:30-8:30pm

Location:
Collective Agency

3050 SE Division, Suite 245 · Portland, OR

We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.

Reply all

Reply to author

Forward

0 new messages