Theme One Program • Exposition
Jon Awbrey
https://inquiryintoinquiry.com/2018/06/08/theme-one-program-exposition-1/
All,
Theme One is a program for building and transforming a particular species
of graph-theoretic data structures, forms designed to support a variety of
fundamental learning and reasoning tasks.
The program evolved over the course of an exploration into the integration of
contrasting types of activities involved in learning and reasoning, especially
the types of algorithms and data structures capable of supporting all sorts of
inquiry processes, from everyday problem solving to scientific investigation.
In its current state, Theme One integrates over a common data structure
fundamental algorithms for one type of inductive learning and one type
of deductive reasoning.
We begin by describing the class of graph-theoretic data structures
used by the program, as determined by their local and global aspects.
It will be the usual practice to shift around and to view these graphs
at many different levels of detail, from their abstract definition to
their concrete implementation, and many points in between.
The main work of the Theme One program is achieved by building and
transforming a single species of graph-theoretic data structures.
In their abstract form these structures are closely related to the
graphs that are called “cacti” and “conifers” in graph theory,
so we'll generally refer to them under those names.
The graph-theoretic data structures used by the program are built up from
a basic data structure called an “idea-form flag”. That structure is defined
as a pair of Pascal data types by means of the following specifications.
Box 1. Type Idea = ^Form
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-type-idea-5eform.png
An “idea” is a pointer to a “form”.
A “form” is a record consisting of:
A “sign” of type char;
Four pointers, as, up, on, by, of type idea;
A “code” of type numb, that is, an integer in [0, max integer].
Represented in terms of “digraphs”, or directed graphs, the combination
of an “idea” pointer and a “form” record is most easily pictured as an arc,
or directed edge, leading to a node that is labeled with the other data,
in this case, a letter and a number.
At the roughest but quickest level of detail, an idea of a form can be drawn like this.
Box 2. Idea^Form Node
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-idea5eform-node.png
When it is necessary to fill in more detail, the following schematic pattern can be used.
Box 3. Idea^Form Flag
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-idea5eform-flag.png
The idea-form type definition determines the local structure of
the whole host of graphs used by the program, including a motley
array of ephemeral buffers, temporary scratch lists, and other
graph-theoretic data structures used for their transient utilities
at specific points in the program.
I will put off discussing these more incidental graph structures
until the points where they actually arise, focusing here on the
particular varieties and the specific variants of cactoid graphs
that constitute the main formal media of the program's operation.
Regards,
Jon
Jon Awbrey
https://inquiryintoinquiry.com/2022/06/16/theme-one-program-exposition-2-2/
Re: Theme One Program • Exposition 1
https://inquiryintoinquiry.com/2022/06/15/theme-one-program-exposition-1-2/
All,
The previous post described the elementary data structure
used to represent nodes of graphs in the Theme One program.
This post describes the specific family of graphs employed
by the program.
Figure 1 shows a typical example of a “painted and rooted cactus”.
Figure 1. Painted And Rooted Cactus
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-painted-and-rooted-cactus-display.png
The graph itself is a mathematical object and does not inhabit the
page or other medium before our eyes, and it must not be confused
with any picture or other representation of it, anymore than we’d
want someone to confuse us with a picture of ourselves, but it’s
a fair enough picture, once we understand the conventions of
representation involved.
Let V(G) be the set of nodes in a graph G and let L be a set of identifiers.
We often find ourselves in situations where we have to consider many different
ways of associating the nodes of G with the identifiers in L. Various manners
of associating nodes with identifiers have been given conventional names by
different schools of graph theorists. I will give one way of describing
a few of the most common patterns of association.
• A graph is “painted” if there is a relation between its node set
and a set of identifiers, in which case the relation is called
a “painting” and the identifiers are called “paints”.
• A graph is “colored” if there is a function from its node set
to a set of identifiers, in which case the function is called
a “coloring” and the identifiers are called “colors”.
• A graph is “labeled” if there is a one-to-one mapping between
its node set and a set of identifiers, in which case the mapping
is called a “labeling” and the identifiers are called “labels”.
• A graph is said to be “rooted” if it has a unique distinguished node,
in which case the distinguished node is called the “root” of the graph.
The graph in Figure 1 has a root node marked by the “at” sign or amphora
symbol “@”.
The graph in Figure 1 has eight nodes plus the five paints in the
set {a, b, c, d, e}. The painting of nodes is indicated by drawing
the paints of each node next to the node they paint. Observe that
some nodes may be painted with an empty set of paints.
The structure of a painted and rooted cactus may be encoded in the form of
a character string called a “painted and rooted cactus expression”. For the
remainder of this discussion the terms “cactus” and “cactus expression” will
be used to mean the painted and rooted varieties. A cactus expression is
formed on an alphabet consisting of the relevant set of identifiers, the
“paints”, together with three punctuation marks: the left parenthesis,
the comma, and the right parenthesis.
Regards,
Jon
Jon Awbrey
https://inquiryintoinquiry.com/2022/06/17/theme-one-program-exposition-3-2/
All,
My earliest experiments coding logical graphs as dynamic “pointer”
data structures taught me conceptual and computational efficiencies
of a critical sort could be achieved by generalizing their abstract
graphs from trees to the variety graph theorists know as “cacti”.
The genesis of that generalization is a tale worth telling another
time, but for now it's best to jump right in and proceed by way of
generic examples.
Figure 1 shows a typical example of a painted and rooted cactus.
Figure 1. Painted And Rooted Cactus
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-painted-and-rooted-cactus-display.png
cactus graphs and cactus strings, demonstrated on the cactus
from Figure 1. By way of convenient terminology, the polygons
of a cactus graph are called its “lobes”. An edge not part of
a larger polygon is called a “2-gon” or a “bi-gon”. A terminal
bi-gon is called a “spike”.
Figure 2. Cactus Graph and Cactus Expression
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-cactus-graph-and-cactus-expression.png
The correspondence between a cactus graph and a cactus string is
obtained by an operation called “traversing” the graph in question.
• One traverses a cactus graph by beginning at the left hand side
of the root node, reading off the list of paints one encounters
at that point. Since the order of elements at any node is not
significant, one may start the cactus string with that list of
paints or save them for the end. We have done the latter in
this case.
• One continues by climbing up the left hand side of the leftmost lobe,
marking the ascent by means of a left parenthesis, traversing whatever
cactus one happens to reach at the first node above the root, that done,
proceeding from left to right along the top side of the lobe, marking each
interlobal span by means of a comma, traversing each cactus in turn one meets
along the way, on completing the last of them climbing down the right hand side
of the lobe, marking the descent by means of a right parenthesis, then traversing
each cactus in turn, in left to right order, that is incident with the root node.
The string of letters, parentheses, and commas one obtains by this procedure
is called the “traversal string” of the graph, in this case, a “cactus string”.
Regards,
Jon
Jon Awbrey
https://inquiryintoinquiry.com/2022/06/20/theme-one-program-exposition-4/
All,
It is possible to write a program that parses cactus expressions
into reasonable facsimiles of cactus graphs as pointer structures
in computer memory, making edges correspond to addresses and nodes
correspond to records. I did just that in the early forerunners of
the present program, but it turned out to be a more robust strategy
in the long run, despite the need for additional nodes at the outset,
to implement a more articulate but more indirect parsing algorithm,
one in which the punctuation marks are not just tacitly converted
to addresses in passing, but instead recorded as nodes in roughly
the same way as the ordinary identifiers, or “paints”.
Figure 3 illustrates the type of parsing paradigm used by the program,
showing the pointer graph obtained by parsing the cactus expression in
Figure 2. A traversal of this graph naturally reconstructs the cactus
string that parses into it.
Figure 2. Cactus Graph and Cactus Expression
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-cactus-graph-and-cactus-expression.png
https://inquiryintoinquiry.files.wordpress.com/2022/06/theme-exposition-parse-graph-and-traverse-string.png
The pointer graph in Figure 3, namely, the parse graph of a cactus
expression, is the sort of thing we'll probably not be able to resist
calling a “cactus graph”, for all the looseness of that manner of speaking,
but we should keep in mind its level of abstraction lies a step further in
the direction of a concrete implementation than the last thing we called by
that name. While we have them before our mind's eyes, there are several other
distinctive features of cactus parse graphs we ought to notice before moving on.
In terms of idea-form structures, a cactus parse graph begins with a root idea
pointing into a “by”‑cycle of forms, each of whose “sign” fields bears either
a “paint”, in other words, a direct or indirect identifier reference, or an
opening left parenthesis indicating a link to a subtended lobe of the cactus.
A lobe springs from a form whose “sign” field bears a left parenthesis.
That stem form has an “on” idea pointing into a “by”‑cycle of forms,
exactly one of which has a “sign” field bearing a right parenthesis.
That last form has an “on” idea pointing back to the form bearing
the initial left parenthesis.
In the case of a lobe, aside from the single form bearing the closing
right parenthesis, the “by”‑cycle of a lobe may list any number of forms,
each of whose “sign” fields bears either a comma, a paint, or an opening
left parenthesis signifying a link to a more deeply subtended lobe.
Just to draw out one of the implications of this characterization and to
stress the point of it, the root node can be painted and bear many lobes,
but it cannot be segmented, that is, the “by”‑cycle corresponding to the
root node can bear no commas.
Regards,
Jon
Alex Shkotin
--
All contributions to this forum are covered by an open-source license.
For information about the wiki, the license, and how to subscribe or
unsubscribe to the forum, see http://ontologforum.org/info/
---
You received this message because you are subscribed to the Google Groups "ontolog-forum" group.
To unsubscribe from this group and stop receiving emails from it, send an email to ontolog-foru...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/ontolog-forum/cb10d0f6-a02d-93dc-9449-c95701dea79a%40att.net.
alex.shkotin
!0!
"p2 симметричен/коммутативен на TV означает что для каждых x,y из TV: (x p2 y) тождественно (y p2 x)."
Declaration COMM_TV func(TV func(TV TV TV)) definition (p2):(∀x:TV(∀y:TV ((x p2 y)=(y p2 x)) )).
"Declaration EQTV_trans :TV definition ():TRANS_TV(=)."
Declaration EQTV_trans func(TV) definition ():(∀x:TV (∀y:TV (∀z:TV (((x=y) and (y=z)) → (x=z))))).
Jon Awbrey
https://inquiryintoinquiry.com/2022/06/23/theme-one-program-exposition-5/
All,
Lexical, Literal, Logical
=========================
Theme One puts cactus graphs to work in three distinct but related ways,
called their “lexical”, “literal”, and “logical” uses. Those three modes
of operation employ three distinct but overlapping subsets of the broader
species of cacti. Accordingly we find ourselves working with graphs, files,
and expressions of lexical, literal, and logical types, depending on the task
at hand.
The logical class of cacti is the broadest, encompassing the whole species
described above, of which we have already seen a typical example in its
several avatars as abstract graph, pointer data structure, and string
of characters suitable for storage in a text file.
Being a “logical cactus” is not just a matter of syntactic form —
it means being subject to meaningful interpretations as a sign of
a logical proposition. To enter the logical arena cactus expressions
must express something, a proposition true or false of something.
Fully addressing the logical, interpretive, semantic aspect of cactus graphs
normally requires a mind-boggling mass of preliminary work on the details of
their syntactic structure. Practical, pragmatic, and especially computational
considerations will eventually make that unavoidable. For the sake of the
present discussion, however, let’s put a pin in it and fast forward to the
logical substance.
Regards,
Jon
Jon Awbrey
http://inquiryintoinquiry.com/2022/06/24/theme-one-program-discussion-7/
Re: Ontolog Forum
https://groups.google.com/g/ontolog-forum/c/vlsQqvEiIkY
::: Alex Shkotin
https://groups.google.com/g/ontolog-forum/c/vlsQqvEiIkY/m/07uF-WTzDwAJ
<QUOTE AS:>
the last pictures produced ( https://photos.app.goo.gl/pJEGBnNqJRBE7JUT9 ).
This is a picture of a derivation tree (aka AST) for the text of four
statements of context-free grammar of some kind. It is important that
In your case attributes are “sign”, “code”. In my case attributes are:
* node id,
* nonterminal,
** for syntactic nonterminal: rule id used for derivation,
** for lexical nonterminal: value taken from text.
</QUOTE>
Dear Alex,
Many thanks, the Graphviz suite looks very nice and I will
spend some time looking through the docs. I kept a few samples
of my old ASCII graphics, mostly from a sense of nostalgia, but
I've reached a point in reworking my Theme One Exposition where
I need to upgrade the graphics. My original aim was to have the
program display its own visuals, but it doesn't look like I'll
be the one doing that. Visualizing proofs requires animation —
I used to have an app for that bundled with CorelDraw but it
quit working in a previous platform change and I haven't gotten
around to hunting up a new one. At any rate, there's a sampler
of animated proofs in logical graphs on the following page.
* Proof Animations
( https://oeis.org/wiki/User:Jon_Awbrey/ANIMATION#Proof_Animations )
Regards,
Jon
Alex Shkotin
Dear Jon,
The animation is mesmerizing: I would watch and watch. But without the pause, next frame, and playback speed settings, it's just a work of art that calls to see it step by step.
And on page [1] you start with the double negation theorem.
Have a look at a few of my comments as a reader, and only on the graph topic taken separately.
Let me point out that graph manipulation is best described in terms of graph technique to which any other interpretation (En, Ex) is external.
(J12) It would be nice to explicitly say what do "a", "b", "c" mean, for example, like this: Let "a", "b", "c" be some graphs.
(Ax) Axioms do not say that graph operations have a parameter or two. This is clear only from the diagram of the proof. And the parameter is most likely an arbitrary graph?
(Insert) Let us consider the application of the Insert operation of axiom J1 in the proof of Double negation.

What is this parameter "(a)"? From [2] we see that this is
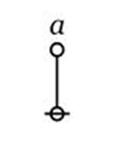
i.e. some graph with a true-node?
My Insert command algorithm turned out like this.
operation Insert
input:
-Let CG0 is a graph under transformation.
--precondition: CG0 has at least one arc.
-Let the arc e1 and the nodes v1, v2 adjacent to it are selected in CG0.
- Let CG1 be a graph to be inserted.
--precondition: CG1 has one true-node.
algorithm:
-create a copy of the graph CG1, designating it CG2.
-put the true-node of CG1 under v1.
-put the true-node of CG2 under v2.
END
“put node v3 under the node v4.” means put it together but take attributes from v4.
So v1, v2 are not true-nodes after Insert.
Later we meet Insert

It is not clear here whether "a" has a single true-node?
Anyway, I can’t get the algorithm from the picture for J1, so I don’t know if my version is correct.
It would be better to describe each operation separately and algorithmically, including specifying all parameters. As algorithms need the most accuracy in math ;-)
I understand that for your amazing project, these are small things. But they will help the programmer to readJ
At the end let me point out the opinion about a proof I like very much: proof itself is a kind of expression where sentences are arguments of derivation rules. To keep it condensed, proof becomes a lattice…
Best wishes,
Alex Shkotin
[1] https://oeis.org/wiki/Propositional_Equation_Reasoning_Systems
[2] https://oeis.org/wiki/Theme_One_Program_%E2%80%A2_Logical_Cacti
--
All contributions to this forum are covered by an open-source license.
For information about the wiki, the license, and how to subscribe or
unsubscribe to the forum, see http://ontologforum.org/info/
---
You received this message because you are subscribed to the Google Groups "ontolog-forum" group.
To unsubscribe from this group and stop receiving emails from it, send an email to ontolog-foru...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/ontolog-forum/6def8460-3286-06db-a77b-87f7d02f792e%40att.net.
Jon Awbrey
http://inquiryintoinquiry.com/2022/06/27/theme-one-program-discussion-8/
https://groups.google.com/g/ontolog-forum/c/vlsQqvEiIkY/m/m2ESSeyeBQAJ
Re: Theme One Program • Exposition 4
https://inquiryintoinquiry.com/2022/06/20/theme-one-program-exposition-4/
Re: Logical Graphs • Animated Proofs
https://oeis.org/wiki/User:Jon_Awbrey/ANIMATION#Proof_Animations
<QUOTE AS:>
the pause, next frame, and playback speed settings, it's just a work
of art that calls to see it step by step.
And on page [1]
Have a look at a few of my comments as a reader, and only on the
</QUOTE>
Dear Alex,
Thanks for viewing the animations and taking the time to work through that
first proof. Clearly a lot could be done to improve the production values —
what you see is what I got with whatever app I had umpteen years ago.
For the time being I'm focusing on the implementation layer of the
Theme One Program, which combines a learning component and a reasoning
component. The first implements a two‑level sequence learner and the
second implements a propositional calculator based on a variant of
Peirce's logical graphs. (I meant to say more about the learning
function this time around but I'm still working up to tackling that.)
To address your comments and questions we'll need to step back for a moment
to a more abstract, implementation-independent treatment of logical graphs.
There's a number of resources along those lines linked on the following
Survey page.
Survey of Animated Logical Graphs
https://inquiryintoinquiry.com/2021/05/01/survey-of-animated-logical-graphs-4/
The blog post “Logical Graphs • Formal Development”
( https://inquiryintoinquiry.com/2008/09/19/logical-graphs-2/ )
gives a quick but systematic account of the formal system
I use throughout. The OEIS wiki article “Logical Graphs”
( https://oeis.org/wiki/Logical_Graphs ) gives a more
detailed development.
Here's an excerpt from the above discussions, giving the four axioms
or “initials” which serve as graphical transformation rules, in effect,
the equational inference rules used to generate proofs and establish
theorems or “consequences”.
Axioms
======
The formal system of logical graphs is defined by a foursome of formal equations,
called “initials” when regarded purely formally, in abstraction from potential
interpretations, and called “axioms” when interpreted as logical equivalences.
There are two “arithmetic initials” and two “algebraic initials”, as shown below.
Arithmetic Initials
===================
Axiom I₁
https://inquiryintoinquiry.files.wordpress.com/2020/09/axiom-i1.png
Axiom I₂
https://inquiryintoinquiry.files.wordpress.com/2020/09/axiom-i2.png
Algebraic Initials
==================
Axiom J₁
https://inquiryintoinquiry.files.wordpress.com/2020/09/axiom-j1.png
Axiom J₂
https://inquiryintoinquiry.files.wordpress.com/2020/09/axiom-j2.png
The statement of the Double Negation Theorem is shown below.
C1. Double Negation Theorem
============================
The first theorem goes under the names of Consequence 1 (C₁),
the double negation theorem (DNT), or Reflection.
Double Negation Theorem
https://inquiryintoinquiry.files.wordpress.com/2021/02/double-negation-3.0.png
The following proof is adapted from the one given by George Spencer Brown
in his book Laws of Form and credited to two of his students, John Dawes
and D.A. Utting.
Double Negation Theorem • Proof
https://inquiryintoinquiry.files.wordpress.com/2021/02/double-negation-proof-3.0.png
That should fill in enough background to get started on your questions …
Regards,
Jon
Alex Shkotin

[3] https://docs.google.com/drawings/d/1Zrjdj7KzqtNQTeOxYT38qBNblKdFpvBgJDCBZwzeAqU/edit?usp=sharing
--
All contributions to this forum are covered by an open-source license.
For information about the wiki, the license, and how to subscribe or
unsubscribe to the forum, see http://ontologforum.org/info/
---
You received this message because you are subscribed to the Google Groups "ontolog-forum" group.
To unsubscribe from this group and stop receiving emails from it, send an email to ontolog-foru...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/ontolog-forum/d6c18510-cc23-2556-bad5-4677d087649f%40att.net.
Jon Awbrey
https://inquiryintoinquiry.com/2022/07/04/theme-one-program-discussion-9/
Re: Theme One Program • Exposition 5
https://inquiryintoinquiry.com/2022/06/23/theme-one-program-exposition-5/
https://groups.google.com/g/ontolog-forum/c/vlsQqvEiIkY/m/_IB_bNCzAAAJ
Dear Alex,
I know the material on sign relations I've been posting lately may seem
a digression from the Theme One Program already in progress but our last
discussions called for pulling the focus on logical graphs back to the
scene of Peirce's semiotics where those graphs work out their fates.
The Fourth is with us in the U.S. — it may be the middle of the week before
my ears stop ringing enough to think straight — but I did just want to touch
base and point out that bit of relevance, especially as I'll need to continue
with the background on sign relations a little longer.
Regards,
Jon
Alex Shkotin
Dear John, happy 4th of July!
The topic of graph processing is my favorite. And I only in the traditions of the ancient Greeks wanted to show instead of animation that the proof is some structure that you can look at and enjoy.
The theme of the sign is utilitarian for me: the sign is the role of a suitable entity in the process of exchanging information and knowledge. It is certainly possible to delve into the types of signs (icons, symbols ...) or expand the idea of a sign to biological processes (as with a sunflower), but this is not mine.
I'll give you an example. Years ago, a friend of mine picked up his home phone only after the second call, when the first ended after three beeps. For him, it was a sign that his friend was calling.
Best holiday wishes,
Alex
--
All contributions to this forum are covered by an open-source license.
For information about the wiki, the license, and how to subscribe or
unsubscribe to the forum, see http://ontologforum.org/info/
---
You received this message because you are subscribed to a topic in the Google Groups "ontolog-forum" group.
To unsubscribe from this topic, visit https://groups.google.com/d/topic/ontolog-forum/vlsQqvEiIkY/unsubscribe.
To unsubscribe from this group and all its topics, send an email to ontolog-foru...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/ontolog-forum/30309b75-39d8-0990-009e-657df5813955%40att.net.
Alex Shkotin
Jon Awbrey
https://inquiryintoinquiry.com/2022/09/29/theme-one-program-exposition-6/
All,
Quickly recapping the discussion so far, we started with
a data structure called an “idea‑form flag” [1] and adopted
it as a building block for constructing a species of graph-
theoretic data structures called “painted and rooted cacti” [2].
We showed how to code the abstract forms of cacti into character
strings called “cactus expressions” [3] and how to parse the
character strings into “pointer structures” [4] in computer memory.
1. https://inquiryintoinquiry.com/2022/06/15/theme-one-program-exposition-1-2/
2. https://inquiryintoinquiry.com/2022/06/16/theme-one-program-exposition-2-2/
3. https://inquiryintoinquiry.com/2022/06/17/theme-one-program-exposition-3-2/
4. https://inquiryintoinquiry.com/2022/06/20/theme-one-program-exposition-4/
At this point we had to choose between two expository strategies.
A full account of Theme One’s operation would describe its use of cactus
graphs in three distinct ways, called “lexical”, “literal”, and “logical”
applications [5]. The more logical order would approach the lexical and
literal tasks first. That is because the program’s formal language learner
must first acquire the vocabulary its propositional calculator interprets as
logical variables. The sequential learner operates at two levels, taking in
sequences of characters it treats as “strings” or “words” plus sequences of
words it treats as “strands” or “sentences”.
5. https://inquiryintoinquiry.com/2022/06/23/theme-one-program-exposition-5/
Finding ourselves more strongly attracted to the logical substance, however,
we leave the matter of grammar to another time and turn to Theme One’s use of
cactus graphs in its reasoning module to represent logical propositions on the
order of Peirce’s alpha graphs and Spencer Brown’s calculus of indications.
Logical Cacti
=============
Up till now we’ve been working to hammer out a two-edged sword of syntax,
honing the syntax of cactus graphs and cactus expressions and turning it
to use in taming the syntax of two-level formal languages.
But the purpose of a logical syntax is to support a logical semantics,
which means, for starters, to bear interpretation as sentential signs
capable of denoting objective propositions about a universe of objects.
One of the difficulties we face is that the words “interpretation”, “meaning”,
“semantics”, and their ilk take on so many different meanings from one moment
to the next of their use. A dedicated neologician might be able to think up
distinctive names for all the aspects of meaning and all the approaches to
them that concern us, but I will do the best I can with the common lot of
ambiguous terms, leaving it to context and intelligent interpreters to
sort it out as much as possible.
The formal language of cacti is formed at such a high level of abstraction that
its graphs bear at least two distinct interpretations as logical propositions.
The two interpretations concerning us here descend from the ones C.S. Peirce
called the “entitative” and the “existential” interpretations of his systems
of graphical logics.
Existential Interpretation
==========================
Table 1 illustrates the existential interpretation of cactus graphs
and cactus expressions by providing English translations for a few
of the most basic and commonly occurring forms.
Table 1. Existential Interpretation
https://inquiryintoinquiry.files.wordpress.com/2022/10/existential-interpretation.png
Entitative Interpretation
=========================
Table 2 illustrates the entitative interpretation of cactus graphs
and cactus expressions by providing English translations for a few
of the most basic and commonly occurring forms.
Table 2. Entitative Interpretation
https://inquiryintoinquiry.files.wordpress.com/2022/10/entitative-interpretation.png
Regards,
Jon
Jon Awbrey
https://inquiryintoinquiry.com/2022/09/30/theme-one-program-exposition-7/
All,
Logical Cacti (cont.)
=====================
The main things to take away from the previous post
( https://inquiryintoinquiry.com/2022/09/29/theme-one-program-exposition-6/ )
are the following two ideas, one syntactic and one semantic:
• The compositional structures of cactus graphs and cactus expressions
are constructed from two kinds of connective operations.
• There are two ways of mapping these compositional structures into
the compositional structures of propositional sentences.
The two kinds of connective operations are described as follows.
• The “node connective” joins a number of component cacti C₁, …, Cₖ to a node:
Node Connective
https://inquiryintoinquiry.files.wordpress.com/2018/04/theme-one-exposition-e280a2-node-connective1.jpg
• The “lobe connective” joins a number of component cacti C₁, …, Cₖ to a lobe:
Lobe Connective
https://inquiryintoinquiry.files.wordpress.com/2018/04/theme-one-exposition-e280a2-lobe-connective1.jpg
The two ways of mapping cactus structures to logical meanings
are summarized in Table 3, which compares the entitative and
existential interpretations of the basic cactus structures,
in effect, the graphical constants and connectives.
Table 3. Logical Interpretations of Cactus Structures
https://inquiryintoinquiry.files.wordpress.com/2022/10/logical-interpretations-of-cactus-structures-e280a2-en-ex.png
Regards,
Jon
Jon Awbrey
http://inquiryintoinquiry.com/2022/10/08/theme-one-program-exposition-8/
All,
Logical Cacti (cont.)
The abstract character of the cactus language relative to its logical
interpretations makes it possible to give abstract rules of equivalence
for transforming cacti among themselves which partition the space of cacti
into formal equivalence classes. The transformation rules and equivalence
classes are “purely formal” in the sense of being indifferent to the logical
interpretation, entitative or existential, one happens to choose.
Two definitions are useful here:
• A “reduction” is an equivalence transformation which applies in the
direction of decreasing graphical complexity.
• A “basic reduction” is a reduction which applies to a basic connective,
either a node connective or a lobe connective.
The two kinds of basic reductions are described as follows.
• A “node reduction” is permitted
if and only if
every component cactus joined to a node itself reduces to a node.
Node Reduction
https://inquiryintoinquiry.files.wordpress.com/2018/04/cactus-graph-e280a2-node-reduction.jpg
• A “lobe reduction” is permitted
if and only if
exactly one component cactus listed in a lobe reduces to an edge.
Lobe Reduction
https://inquiryintoinquiry.files.wordpress.com/2018/04/cactus-graph-e280a2-lobe-reduction.jpg
That is roughly the gist of the rules. More formal definitions
can wait for the day when we have to explain all this to a computer.
Regards,
Jon
