Quaternions are elements of reality but hard to visualize

41 views
Skip to first unread message

Bryan Sanctuary

unread,
May 5, 2022, 9:44:48 AM5/5/22
to Bell inequalities and quantum foundations
Since I find that quaternions are the engine that spins a spin, and it exists in the 4th dimension hyperspace, they are very difficult to visualize.

There is a very good series of animations that I recommend if you want to visualize quaternions.



Chantal Roth

unread,
May 5, 2022, 9:57:26 AM5/5/22
to 'Scott Glancy' via Bell inequalities and quantum foundations
Funny, I recently spent quite a bit of time on how to visualize spin (specifically 1/2) in various ways - of course using quaternions :-) (because quaternions are common in computer graphics..much easier than working with Euler angles:-))

It includes the "Dirac belt trick" an others... in case anyone is interested, I can also give a demo to anyone (since the software is interactive)

And the software (run at your own risk - it requires a good computer - it is better when I demo it myself since it has many settings/parameters :-))

Best wishes,
Chantal
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.

Jay R. Yablon

unread,
May 5, 2022, 10:28:58 AM5/5/22
to Bell_quantum...@googlegroups.com
Keep in mind that William Rowan Hamilton first formulated quaternions in 1843 to mathematically represent the fact that rotations do not commute.  As far as I know this was the first development of non-commuting objects in mathematics.  A few years ago I looked to see if perhaps Gauss had done anything with non-commuting objects, but did not find anything.
 
Spin then uses these quaternions, in the form of non-commuting 2x2 Pauli spin matrices, to represent rotations about a single axis taken by convention to be the z axis.  So in many ways, the best visualization is to just take any object and rotate it by some angle through the x followed by y axis to get xy, then through y followed by x to get yx, then see with your own eyes that xy does not equal yx except for some special cases.

Yang-Mills theory then generalizes the Pauli matrices into NxN matrices, and provides the basis for theoretically describing physics interactions in a general way.

What makes this all rather deep are the Robertson-Schrödinger relations which give you an uncertainty principle ANY TIME you have two non-commuting objects, for the observables represented by those objects.  Then, the question becomes whether that which is uncertain is or is not a physical "element of reality" as that term was used by Einstein-Podolsky-Rosen, which transports you into the middle of a key part of the local realism debate over Bell's theory.  But it all starts in 1843 with Hamilton!

Chantal Roth

unread,
May 5, 2022, 11:06:40 AM5/5/22
to 'Scott Glancy' via Bell inequalities and quantum foundations
Yes - when viewing i (j and k) each as a rotation of 90 degrees around an axis, it is so obvious that ijk=-1 :-), and that way quaternions are not magical at all, but really very practical and simple.

Even computing spin 1/2 visualization is actually VERY easy that way!

You can also do it with a glass of water:
- hold a glass of water (maybe empty at first :-)) in your right hand.
- now try to rotate it *continuously* , following the rules:
- you cannot move your fingers or let go of the glass
- don't break your arm :-)
- you cannot rotate your body or make a head stand
- you may not spill any water :-)

The whole trick is to twist/rotate a chunk of space (elastic solid, represented as a "grid" - imagine a jello pudding with a grid like coordinate system) in a way so that the grid realigns after 720 degrees, without breaking anything of course (like your arm) :-).

It's a simple function of time t and distance r from some center point of the "particle" (or glass in hand)
f(r,t) = q(t) * s(r) * q` (t)

t is a function of time (angle from 0 to 360, based on the time passed, the phase)
r is a function of distance from center:

(the amount of rotation of s(r) decreases with increasing distance, (1/r^2 or 1/r for instance. In the "Dirac belt mode" that angle is 0 exactly at the ends of the belt)

q(t) is rotation around x axis (a quaternion)
s(r) is rotation around the y(or z)  axis (also a quaternion)
q'(t)  is rotation around y axis in opposite direction (conjugate)

You can imagine it as Matryoska type doll: a large number of concentric shells of increasing radius r.
At each point in time t, for each of those shells, the current rotation is computed based on q(t) * s(r) * q` (t).
So the mesh is computed by:
each (invisible) sphere is (literally) rotated (using a quaternion) based on that computation.
The mesh point transforms (which are all on shells) are automatically updated accordingly.

And that results in the Dirac belt visualized (or the glass of water above).
Here is an example with a sphere in the center to see it better (imagine sticking a solid sphere into a pudding, then doing the spin movement as described, and this is what the sphere would do  - from a simple larmor precession to the full "720" rotation). Note the grid never breaks and there are of course no knots either :-).

Best wishes,
Chantal

Jay R. Yablon

unread,
May 5, 2022, 1:26:34 PM5/5/22
to Bell_quantum...@googlegroups.com
Yes -- and I neglected to mention that the 720 degree rotation versus 360 degrees required to return to the same physical circumstance as mentioned by Chantal, is based on the orientation / entanglement reviewed by Misner, Throne and Wheeler in their textbook Gravitation.  Taking an object "tied" to its environment and rotating it by only 360 degrees will entangle the ties; but after 720 degrees they can all be untangled.  Best to all, Jay

Mark Hadley

unread,
May 5, 2022, 2:29:48 PM5/5/22
to Bell_quantum...@googlegroups.com

---------- Forwarded message ---------
From: Mark Hadley <sunshine...@googlemail.com>
Date: Thu, 5 May 2022, 19:27
Subject: Re: spin half and 720 degree rotations
To: Jay R. Yablon <jya...@nycap.rr.com>


The visualisations of spin half described in this thread all involve tethered objects. One end rotates, the other is fixed.

The big puzzle about spin half is why 360 degree rotation is not a symmetry operation. Or alternatively, how can an elementary particle be tethered. 

One explanation, indeed the only one I am aware of, is that particles are geometric structures in spacetime where time is not orientable. 

This not only explains spin half, but is also a mechanism for nonlicality ( contextuality). 

See:

And

Cheers
Mark


Chantal Roth

unread,
May 5, 2022, 3:16:01 PM5/5/22
to 'Scott Glancy' via Bell inequalities and quantum foundations
I agree with the geometric structure - and in particular it works for a model where the universe is a kind of "stiff fabric of spacetime" (or elastic solid).

At least in the spin 1/2 visualizations I mentioned, *all* ends are actually fixed (in all directions :-.)).
If you imagine tying the glass of water with ropes to the walls in your living room in all directions, there are no knots and nothing rips (if the motion is done correctly :-)).

In other words, you could do this in a  (very large and rather robust :-)) jello pudding, and the center would appear to "rotate" continuously, yet the geometry of the pudding stays intact.
(Maybe I will do youtube video on this one day :-)).

Best wishes,
Chantal
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.

Jay R. Yablon

unread,
May 5, 2022, 8:36:55 PM5/5/22
to Bell inequalities and quantum foundations
Mark's comment below about tethering (perhaps another word for entanglement), and Chantel's broaching of similar issues, got me to thinking again about some ideas I had in late 2019 when I was actively participating at this forum -- before I  diverted back to my primary research on particle physics -- regarding  the possibility of reducing Bell’s cosine correlation to a variant manifestation of the Stern Gerlach (SG) result.  So, I decided to dust off something I had drafted back then but never sent out, make some minor edits, and attach it here.  Three pages total so not a long read; not my usual 40+ pages. :-)

The main conclusion in the attached:

"Bell’s negative cosine correlations are no more and no less troublesome than the SG results.  They are both decidedly non-classical.  And Feynman stated that all the essential features of quantum mechanics versus classical physics can be distilled down to the Stern-Gerlach experiment.  But because of [the simple calculations in the attached], to the extent we need to resort to instantaneous action at a distance to explain singlet correlations, we would also need to do so for SG.  Conversely, if we do not have to resort to instantaneous action at a distance to explain SG, the neither do we need to do so for the singlet correlations.

I'd be interested in people's thoughts on this.

Best regards,

Jay

On Thursday, May 5, 2022 at 2:29:48 PM UTC-4 sunshine...@googlemail.com wrote:
...
This not only explains spin half, but is also a mechanism for nonlicality ( contextuality). 
...
SG and Bell Correlations 2.0.pdf

Jay R. Yablon

unread,
May 5, 2022, 8:38:17 PM5/5/22
to Bell inequalities and quantum foundations
Actually, it is only two pages. :-)

Richard Gill

unread,
May 6, 2022, 1:35:36 AM5/6/22
to Jay R. Yablon, Bell inequalities and quantum foundations
I must say that I don’t like your notation. Why is there a script B as a non-argument to function script A? Maths notation has evolved to be very expressive and at the same time very compact; not wasting the reader’s brain-power by distracting it with the task of decoding superfluous symbols.

I’m all in favour of physicists enriching and even revolutionising mathematics by introducing new notations for new concepts. Mathematics mustn’t be “frozen” in its present form. 

I also dislike the notation < …_k> for the limit as n tends to infinity of an average of n terms indexed by k. 

Sent from my iPad

On 6 May 2022, at 02:38, Jay R. Yablon <yab...@alum.mit.edu> wrote:

Actually, it is only two pages. :-)
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.

Chantal Roth

unread,
May 6, 2022, 1:49:45 AM5/6/22
to 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
Re *"The view is held by many that this  cosine  correlation,  rather  than  a  sawtooth  correlation,  can  only  be  explained  by  nonlocal communication between the two detection events."

Here is an interesting spin (no pun intended) on the topic :-)

In (very) short: "...  assuming a strict phase correlation of the photons at the source the observed polarization correlation can be deduced from wave optical considerations" 

Basically: the cos shaped correlation is due to Malus law - at least when using polarizers.
So nothing magical or weird at all :-). No non-locality required.
(I would love to see an experiment that does *not *use polarizers... )

A provoking remark from the end:
"Bell's inequality is misleading because it attributes properties like polarization directions to particles and not to waves. Therefore, Bell cannot take into account phase differences of entangled photons. In future one should ignore violations of Bell's theorem because Bell's considerations are not adequate to describe wave phenomena."

Maybe we should invite the author to the discussion :-).
(cc-ed here :-))

Best wishes,
Chantal
ShoThe view is held by many that this cosine correlation, rather than a sawtooth correlation, can only be explained by nonlocal communication between the two detection events
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.


Attachments:
  • SG and Bell Correlations 2.0.pdf

Richard Gill

unread,
May 6, 2022, 4:54:02 AM5/6/22
to Chantal Roth, Bell Inequalities and quantum foundations, ju...@physik.uni-kl.de
No puzzle at all from a wave point of view why we see sines and cosines in the joint joint intensities of ++, +-, -+ and — detections.

The puzzle is that the detections are close to simultaneous detections of single particle-like events in each wing of the experiment. Widely separated in space and time.

And you don’t have to call it “weird”. It is weird according to the simple picture of reality which has been built into our ape brains by evolution. You can also call it wonderful, or amazing. Nature often gives cause for amazement or wonderment. The more we know about it the more we know what we don’t know.

Austin Fearnley

unread,
May 6, 2022, 5:10:24 AM5/6/22
to Bell inequalities and quantum foundations
Hi Jay and Chantal

Chantal says:     'someone' would like to see a Bell experiment without polarisers?
Also Jay explains that Malus's formula dovetails very well into a table of Bell experiment outcomes.

The problem is that Malus has polarised beams as inputs whereas Bell does not.  I assume that the Bell oven produces beams of randomly joint-polarised pairs of particles.
One can use Malus's Laws to solve the Bell experiment only if one can force Bell measurements to be based on polarised beams.
One way to do this is to make positrons travel backwards in time.  A retrocausal solution solves this problem, but would need to change our view of reality.  
I have a paper on this solution.

Best wishes to Jay and Chantal!

Chantal Roth

unread,
May 6, 2022, 7:29:33 AM5/6/22
to Richard Gill, 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
Yes, this also works for widely separated events.
It even works for *non* entangled photon sources (we have actually briefly discuss this before :-)

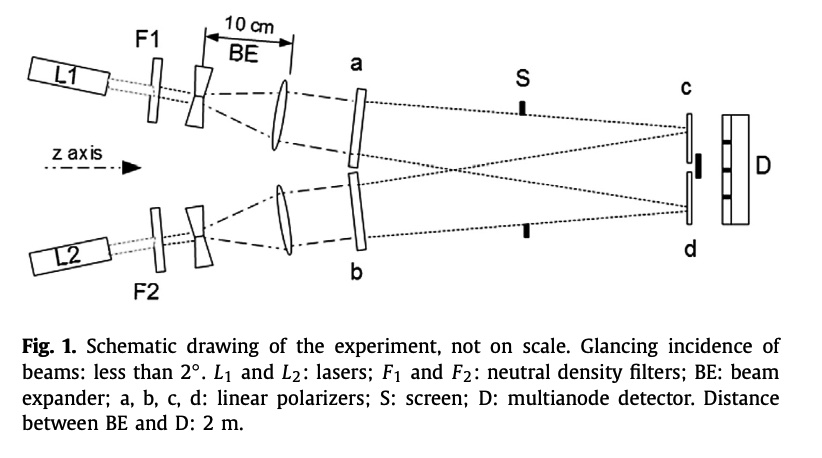
Using to separate photon beams that are not physically connected, to do a Bell type experiment.
"Bell-type Polarization Experiment With Pairs Of Uncorrelated Optical Photons"

"Bell-type Polarization Experiment With Pairs Of Uncorrelated Optical Photon.
We present a Bell-type polarization experiment using two independent sources of polarized optical photons, and detecting the temporal coincidence of pairs of uncorrelated photons which have never been entangled in the apparatus. Very simply, our measurements have tested the quantum-mechanical equivalent of the classical Malus’ law on an incoherent beam of polarized photons obtained from two separate and independent laser sources greatly reduced in intensities.The outcome of the experiment gives evidence of violation of the Bell-like inequalities."


The detection of photons depends on the intensity. So if this intensity is a function of the angle, then of course it takes "more photons"  to go through the detector to measure the photons.
This is like discarding data, which looks like the detection loophole. The issue then is how we *measure* photons at the detector, and has nothing to do with *any* kind of magical entanglement.

So maybe the problem is that we are calling it a "loophole" when in fact it is an essential part of measuring photons...

That is why I would want to see a result that does *not* use photons over large distances... or at least an experiment that does not involve the Malus law.

Best wishes,
Chantal

Richard Gill

unread,
May 6, 2022, 7:43:32 AM5/6/22
to Chantal Roth, 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
Dear Chantal

In the 2015 experiments at Vienna and at NIST, the experimental unit is *time-slot*, not “particle pair”. No time-slots are discarded. Every time-slot delivers two binary outcomes (and received two binary setting choices). The experiments in Delft and Munich are a bit more complicated; they are three-party Bell-type experiments, not classical two-party experiments. In Delft they measured the spins of electrons in a Nitrogen-vacancy defect in a diamond crystal.

Richard

Sent from my iPad

On 6 May 2022, at 13:29, Chantal Roth <cr...@nobilitas.com> wrote:



Jay R. Yablon

unread,
May 6, 2022, 9:10:02 AM5/6/22
to Bell inequalities and quantum foundations
I find it encouraging the worst thing Richard can say about what I posted is that he does not like the notation. 🤣

Substantively, do others agree that it is worth looking hard at whether Bell’s cosine correlation can be reduced to and explained as a variant of the Stern-Gerlach experiment result?

Best regards, Jay

On May 6, 2022, at 1:35 AM, Richard Gill <gill...@gmail.com> wrote:

I must say that I don’t like your notation. Why is there a script B as a non-argument to function script A? Maths notation has evolved to be very expressive and at the same time very compact; not wasting the reader’s brain-power by distracting it with the task of decoding superfluous symbols.

Richard Gill

unread,
May 6, 2022, 10:25:26 AM5/6/22
to Jay R. Yablon, Bell inequalities and quantum foundations
Substantively, I don’t think it is worth looking to see if the cosine correlation predicted by quantum mechanics can be “reduced” to a Stern-Gerlach type story. It works the other way round. A Bell type experimental protocol avoids all the “loopholes” one could imagine in the analogous Stern-Gerlach type game. Bell is Stern-Gerlach repeated measurements reduced to essentials and bringing in non-locality. You could say: two-slit experiment meets Stern-Gerlach in EPR-B.

And it is not specifically about photons and polarization. In its simplest form it’s about spin-half systems, in their abstract form.

I’d recommend that Jay studies two of my papers on the cosine business. The first one (about to appear in Entropy) about a proof of Bell’s theorem using Fourier analysis, the second one (published in Entropy two years ago) about all the other curves (apart from the negative cosine) which classical (semi-deterministic) physics can generate.

Gull's theorem revisited

Steve Gull, in unpublished work available on his Cambridge University homepage, has outlined a proof of Bell's theorem using Fourier theory. Gull's philosophy is that Bell's theorem (or perhaps a key lemma in its proof) can be seen as a no-go theorem for a project in distributed computing with classical, not quantum, computers. We present his argument, correcting misprints and filling gaps. In his argument, there were two completely separated computers in the network. We need three in order to fill all the gaps in his proof: a third computer supplies a stream of random numbers to the two computers representing the two measurement stations in Bell's work. One could also imagine that computer replaced by a cloned, virtual computer, generating the same pseudo-random numbers within each of Alice and Bob's computers. Either way, we need an assumption of the presence of shared i.i.d. randomness in the form of a synchronised sequence of realisations of i.i.d. hidden variables underlying the otherwise deterministic physics of the sequence of trials. Gull's proof then just needs a third step: rewriting an expectation as the expectation of a conditional expectation given the hidden variables.

https://arxiv.org/abs/1312.6403

The triangle wave versus the cosine: How classical systems can optimally approximate EPR-B correlations

The famous singlet correlations of a composite quantum system consisting of two spatially separated components exhibit notable features of two kinds. The first kind consists of striking certainty relations: perfect correlation and perfect anti-correlation in certain settings. The second kind consists of a number of symmetries, in particular, invariance under rotation, as well as invariance under exchange of components, parity, or chirality. In this note, I investigate the class of correlation functions that can be generated by classical composite physical systems when we restrict attention to systems which reproduce the certainty relations exactly, and for which the rotational invariance of the correlation function is the manifestation of rotational invariance of the underlying classical physics. I call such correlation functions classical EPR-B correlations. It turns out that the other three (binary) symmetries can then be obtained "for free": they are exhibited by the correlation function, and can be imposed on the underlying physics by adding an underlying randomisation level. We end up with a simple probabilistic description of all possible classical EPR-B correlations in terms of a "spinning coloured disk" model, and a research programme: describe these functions in a concise analytic way. We survey open problems, and we show that the widespread idea that "quantum correlations are more extreme than classical physics allows" is at best highly inaccurate, through giving a concrete example of a classical correlation which satisfies all the symmetries and all the certainty relations and which exceeds the quantum correlations over a whole range of settings

Richard Gill

unread,
May 6, 2022, 10:56:20 AM5/6/22
to Chantal Roth, 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
Chantal, you should read that paper by the Italians M. Iannuzzi, R. Francini, R. Messi and D. Moricciani a bit more carefully. They have two independent beams, four polarization filters, set at angles a, b, c and d, and they keep three of the settings fixed and just vary the fourth. Their “violation of Bell inequalities” is a charade. It shows that are clever in classical optical engineering and in putting up a smoke-screen of obfuscation.

You also referred to one of Caroline Thompson’s papers. Long, long ago, she used the detection loophole and some ingenuity to come up with models which provided a classical explanation of the earliest Bell type experiments. Ie the very imperfect experiments of more than 40 years ago. Her work certainly goaded the subsequent rapid improvement of Bell type experiments.

Malus’ law holds in classical optics because it is the deterministic “large number” limit of quantum theory; and it turns up there simply because of the “wave” component of quantum theory.

Not because of photons.

Sent from my iPhone

On 6 May 2022, at 13:29, Chantal Roth <cr...@nobilitas.com> wrote:



Алексей Никулов

unread,
May 6, 2022, 11:13:06 AM5/6/22
to Jay R. Yablon, Richard Gill, Chantal Roth, 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
Dear Jay,

Bell’s cosine correlation is deduced from the Bohr jump and the
operator of finite rotation of the coordinate axes, (see paragraph 58
of the book [1]) rather than only the Stern-Gerlach experiment result.
The same cosine correlation sin^{2}f/2 – cos^{2}f/2 = – cos f is
deduced from the Dirac jump and the operator of finite rotation of the
coordinate axes when single particles are measured two times in
different directions z1 and z2 with the angle f between z1 and z2, see
section 4. THE ASSUMPTION USED AT THE DEDUCTION OF THE GHZ THEOREM
MAKES IMPOSSIBLE THE PREDICTION OF VIOLATION OF BELL’S INEQUALITIES in
my manuscript “Physical thinking and the GHZ theorem” see attached
file. Dirac postulated in 1930 ”that a measurement always causes the
system to jump into an eigenstate of the dynamical variable that is
being measured” [2]. The spin state is the eigenstate, State =
|+>_{z1} along z1 and the superposition of state

State= |+>_{z1} = cos f/2 |+>_{z2} - sin f/2 |->_{z2} (1)

along any other direction after the first measurement of spin
projection along z1. The operator of finite rotation of the coordinate
axes about the y-axis [1] is used in (1). According to (1) the
probability to repeat at the second measurement along z2 the result at
the first measurement along z1 equals cos^{2}f/2 and to obtain the
opposite result equals sin^{2}f/2.

I demonstrate in my manuscript “Physical thinking and the GHZ theorem”
that the conclusion about violation of the obvious inequality (4) at
measurements of single particles repeats the conclusion made by Bell
in “Bertlmann’s socks” [3] about violation of Bell’s inequality ((8)
in my manuscript) for two particles of the EPR pair. It is important
to emphasize that the orthodox quantum mechanics predicts the
violation of the obvious inequality (4) because operators acting on
one particle do not commute. But the orthodox quantum mechanics cannot
predicts the violation of Bell’s inequality (8) because operators
acting on different particles commute.

Bell followed Bohm’s quantum mechanics rather than the orthodox
quantum mechanics. Only the measured particle jump into an eigenstate
of the dynamical variable that is being measured according to the
orthodox quantum mechanics. The particles of the EPR pair (1) jump to
the state (2) in my manuscript according to the Dirac jump. No
correlation between results of the observations of two particles of
the EPR pair is in this case. Quantum mechanics can predict the EPR
correlation if only not only measured particle but also the particle
which is not measured jumps into an eigenstate of the dynamical
variable that is being measured, i.e. if two particles of the EPR pair
jump to the state (3) rather than the state (2) in my manuscript. Bohm
postulated this jump of both particles in 1951. I call this jump the
Bohr jump since Bohr was the first who claimed in 1935 that
measurement of one particle can change the quantum state of other
particle.

[1] L. D. Landau, E. M. Lifshitz, Quantum Mechanics: Non-Relativistic
Theory (Volume 3, Third Edition, Elsevier Science, Oxford, 1977).
[2] A.M. Dirac, The Principles of Quantum Mechanics. Oxford University
Press, New York, 1958
[3] J.S. Bell, Bertlmann’s socks and the nature of reality. J. de
Physique 42, 41 (1981).
With best wishes,

Alexey

пт, 6 мая 2022 г. в 17:56, Richard Gill <gill...@gmail.com>:
> --
> You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.
> To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/3E5BDA29-1D5C-426A-9495-9719F4D6D122%40gmail.com.
Bell_GHSZ.pdf

Richard Gill

unread,
May 6, 2022, 12:10:19 PM5/6/22
to Алексей Никулов, Jay R. Yablon, Chantal Roth, 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
I would calculate the probabilities from the expectation values: <A>, <B>, <A^2>, <B^2>, <AB> using the usual QM formulas and the state rho = | Psi > < Psi |. Here, A and B are shorthand for A tensor product identity, and identity tensor product B, respectively. The Hilbert space is C^2 tensor product C^2.

It seems that Alexei does not know this approach.

Sent from my iPhone

> On 6 May 2022, at 17:13, Алексей Никулов <nikulo...@gmail.com> wrote:
>
> Dear Jay,
Bell_GHSZ.pdf

Richard Gill

unread,
May 6, 2022, 12:31:51 PM5/6/22
to Алексей Никулов, Jay R. Yablon, Chantal Roth, 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
PS I made no assumption of any Dirac jump. I assumed that obervables are represented by self-adjoint operators and can be measured. A collection of commuting observables can be represented as functions of one observable and can therefore be measured simultaneously.

Sent from my iPhone

> On 6 May 2022, at 18:10, Richard Gill <gill...@gmail.com> wrote:
>
> I would calculate the probabilities from the expectation values: <A>, <B>, <A^2>, <B^2>, <AB> using the usual QM formulas and the state rho = | Psi > < Psi |. Here, A and B are shorthand for A tensor product identity, and identity tensor product B, respectively. The Hilbert space is C^2 tensor product C^2.
Bell_GHSZ.pdf

Алексей Никулов

unread,
May 6, 2022, 12:57:48 PM5/6/22
to Richard Gill, Jay R. Yablon, Chantal Roth, 'Scott Glancy' via Bell inequalities and quantum foundations, ju...@physik.uni-kl.de
Dear Richard,

You should finally understand that the prediction of the violation of
Bell's inequalities by quantum mechanics is based on quantum mechanics
rather than mathematics. Therefore, your approach has nothing to do
with the prediction by quantum mechanics of the violation of Bell
inequalities. You have to understand why quantum mechanics, and which
quantum mechanics, predicts the violation of Bell inequalities. You
have to understand that without the Dirac jump quantum mechanics
cannot predicts violation even the obvious inequality (4) in my
manuscript at measurements of single particles. Operators acting on a
single particle do not commute precisely because of the Dirac jump.

With best wishes,
Alexey

пт, 6 мая 2022 г. в 19:31, Richard Gill <gill...@gmail.com>:

Austin Fearnley

unread,
May 6, 2022, 2:08:16 PM5/6/22
to Bell inequalities and quantum foundations
Jay

I have a paper on this topic at https://vixra.org/abs/2006.0160

The paper shows that Malus's Law is very relevant to Bell's Theorem, but only in a retrocausal context.  As I wrote previously, Malus requires polarised particles as input, whereas a Bell experiment presumably uses randomly polarised particles as input.

I did explore the S-G results and wrote a computer program of which a listing is appended to my paper:
"APPENDIX Computer program to produce results for Malus’s Law
intensities using local hidden variables in a particle-at-a-time simulation".
I note that there is already a thread here on that topic by pierrel5556, from December 2021.

Richard:
"Not because of photons" ...  That is a strange comment?

My model for photons and electrons uses reverse engineering from Malus's Law to get a glimpse of the individual particle behaviours.  I like Bryan's ideas though I have not followed all the maths.  My model has a gyroscopic periodic variation (phase) about a fixed polarisation angle (e.g. UP) and the phase determines a measurement outcome.  As it was reverse engineered from Malus it is no surprise that I can get measurements to agree with Malus.
But ... when I made a simulation for a Bell correlation it did not give -0.707.  It did not even give -0.5.  It actually gave approximately -0.35 (from memory as I did not write this up).  I predict that if Bryan's formulae are converted into a simulation, then the correlation will also be less in absolute magnitude than -0.5.  I like Bryan's ideas but nothing can defeat the Bell inequality.  Retrocausality does not defeat the inequality but the new physics makes the Bell experiment produce NOT a correlation of pairs of entangled states, so retrocausality renders Bell to be bypassed.

Richard Gill

unread,
May 7, 2022, 12:11:20 AM5/7/22
to Алексей Никулов, Bell Inequalities and quantum foundations
Dear Alexei

I understand quantum mechanics as many physicists do today. I don’t know your version of quantum mechanics and I have no need to.

Richard

Sent from my iPhone

> On 6 May 2022, at 18:57, Алексей Никулов <nikulo...@gmail.com> wrote:
>
> Dear Richard,

Алексей Никулов

unread,
May 7, 2022, 7:07:23 AM5/7/22
to Richard Gill, Bell Inequalities and quantum foundations
Dear Richard,

Perhaps you understand quantum mechanics as many physicists do today.
But you have to understand quantum mechanics as John Bell rather than
many physicists in order to understand how Bell deduced violation of
Bell’s inequalities from quantum mechanics. Many physicists, like you,
do not know that quantum mechanics is unthinkable without the Dirac
jump, since the Dirac jump is not written about in many textbooks, for
example in a well-known book [1]. I know that many physicists are sure
that there is no jump at all in the book [1]. Bell, in contrast to
many physicists, understood that the jump is in the book [1]. He
called this jump the LL (Landau – Lifshitz) jump and explained in the
section “The quantum mechanics of Landau and Lifshitz” of his famous
work “Against Measurement” [2] the fundamental difference between the
Dirac jump and the LL jump.

L. D. Landau, E. M. Lifshitz postulated in [1] that the measuring
device can jump into an eigenstate by itself, and not its eigenstate,
but the eigenstate of the measured quantum system. I argue in the
manuscript “Physical thinking and the GHZ theorem” that the rejection
of realism by the creators of quantum mechanics has resulted in
rejection of physical thinking. The absurd postulate about the jump of
the measuring device into an eigenstate of the measured system
indicates a complete rejection of physical thinking.

Many physicists, in contrast to Bell, do not understand that the LL
jump is the obvious absurd postulated in [1] and like books. Bell
noted in [2] that “Landau sat at the feet of Bohr”. Bohr and other
creators of quantum mechanics have misled most physicists by falsely
substituting ‘measurement’ for ‘observation’. Therefore, most
physicists did not understand for a long time that quantum mechanics
contradicts realism. This topic became fashionable, even to the point
that mathematicians and chemists began to study it, only because of
Bell's inequalities, which were misunderstood by many physicists.

[1] L. D. Landau, E. M. Lifshitz, Quantum Mechanics: Non-Relativistic
Theory (Volume 3, Third Edition, Elsevier Science, Oxford, 1977).

[2] J.S. Bell, Against Measurement. in the proceedings of 62Years of
Uncertainty. Plenum Publishing, New York 1989; Phys. World 3, 33-40
(1990)

With best wishes,

Alexey

сб, 7 мая 2022 г. в 07:11, Richard Gill <gill...@gmail.com>:

Chantal Roth

unread,
Jun 1, 2022, 1:45:54 AM6/1/22