Re: Local hidden variables.
Richard Gill
The Bell inequalities and quantum foundations group is exclusively for quantum theory and related topics. It was founded (and is *owned*) by Alexandre de Castro. It has two *managers* - Alexandre de Castro and Richard Gill. We (the managers) try to "manage" as little as possible. We rely on the self-discipline of group members to keep discussion threads "on topic" etc. etc. Please keep civilized and friendly even if you totally disagree with other members of the group, and especially when someone tells you that they think that your ideas are wrong. The idea is that here, ideas do clash! We are not a mutual admiration society. If you have technical problems using the Google Groups "platform" please contact Richard by email, gill...@gmail.com
On 24 Feb 2023, at 08:36, Bryan Sanctuary <bryancs...@gmail.com> wrote:If anyone copied here does not want to get these, please let me know and i will remove you and apologize for including you.Hi MarkI agree it is a linear relationship. As I say, your expression is the way I look at how various contributions from pol and coherence are related. In my program I calculated the two complementary parts separately, giving values that are independent of how many clicks are actually produced.In real experiments, sometimes there is more of one than the other, and the experimental clicks are all accounted for with a probability for each. To me this is clear and accounts for the experimental results, click by click.It also shows that Richard's last objection, dividing my result by two, is not validated. He has exhausted all his objections, but I invite him to have a go at trying to show my work is flawed.The next part to understand is the difference between polarization clicks and coherence clicks. I suggest a filter to separate them, but the important point is to show that depending on the difference between the filter settings of Alice and Bob, one is favoured over the other.The fundamental physical idea is what I explained before and for which there is ample evidence from other experiments. That is, spins decoupling and coupling occurs as a function of field (filter settings). The coherence state forms from the coupling of the two spin 1/2 to give a coherent spin 1, and this is maintained at filter settings that differ by pi/4. As the difference moves to pi/2 or to zero, that coherence decouples and the coherence is lost leaving only polarized states.That is the mechanism. I requires a lot of changes to our understanding of the usual spin of 1/2 that is measured, but it is all well based in QFT.I am working on wording in my papers all the time, and I hope that my pedagogical videos will spell things out.In the meantime, I hope you agree that your distribution of pol and coh is one step to accepting my approach. I very much appreciate your input and tenacity which helps me in clarifications and suggest better ways to put these ideas across.Thank youBryanOn Thu, Feb 23, 2023 at 10:45 AM Mark Hadley <drmark...@gmail.com> wrote:Dear Bryan,That was a good summary apart from one sentence.It's a linear relationship. It can't be anything else. The correlation moves from pol to col as the fraction shifts from one to the other.It's not just about combining correlations. It's true for the average values of any complementary populations that are mixed.CheersMarkOn Thu, 23 Feb 2023, 13:44 Bryan Sanctuary, <bryancs...@gmail.com> wrote:Hi MarkI now have your figure and I think it agrees with me. If we have only pol, then i get the pol correlation. If we have only col and no pol, then i get only coh correlation. The last equation says some pol and some coh and you add them. The prefactors simply gives the intensity of each.The ratios say over Ntot coincidences, sometimes you have one and sometimes you have the other in those ratios. But you never have the two together. If you filtered and collected them in separate bins then the number of coincidences are divided in those ratios between those bins. Then the two correlation are obtained separately and accumulate as the sum.If you have 3/4 pol and 1/4 coh that does not mean you multiply pol by 3/4 and coh by 1/4, it just means you have more coincidence from pol and fewer from coh.I think that is consistent with what I am saying.BryanOn Thu, Feb 23, 2023, 10:30 Mark Hadley <drmark...@gmail.com> wrote:Dear Richard and Bryan,Yes a trivial error on equation 3. I've corrected that.And I have changed the result to deal with cases where the p and e populations are unequal.It's straightforward algebra. And gives a sensible result. Bryan was right to start with a definition of correlation. That is what I have done.Bryan,Can you follow and agree with this derivation?ThanksMarkOn Thu, 23 Feb 2023, 04:56 Richard Gill, <gill...@gmail.com> wrote:Dear Bryan, MarkSorry, I first sent this to Udi and Bryan, by mistake. Another try.Bryan: When we calculate correlations we divide by the number of pairs of particles, not the number of particles.Mark: your handwritten note contains an obvious misprint on line 3 I think, but I agree with your conclusionTo Bryan again, all of Mark’s “N”s are numbers of particle pairs. In his line 1, N_tot is the total number of particle pairs.A particle pair can be of type pol, or of type cohThe two particles of a pair either lead to the same outcome or they lead to opposite outcomes.Mark: do you agree that your line 3 is wrong? Perhaps you should correct it for Bryan.RichardPS I’m not sending this email to Jarek’s group because Jarek and other members of his group are getting annoyed by all the messages about Bell’s theorem. Jarek’s group is not about Bell’s theorem, it is about the nature of time.
Bryan Sanctuary
Bryan Sanctuary
Dear Bryan and Richard,So I have produced relevant equations that all three of us agree on.They are simple and can't sensibly be anything else.Bryan, thank you for engaging with this so positively.CheersMark
Richard Gill
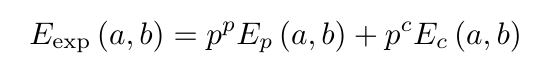
On 24 Feb 2023, at 11:16, Bryan Sanctuary <bryancs...@gmail.com> wrote:
Hi RichardYou are categorically and unequivocally wrong. The two correlations are observed in coincidence experiments and over a large number of runs and different filter angle settings, are observed as a mixing of the two according to the probabilities. Here it is
Mark Hadley
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/CALLw9Yx5dGUTGU3qAo2TquiDAGu8nvEMW4DKEkjJGZV-pmbSQg%40mail.gmail.com.
Bryan Sanctuary
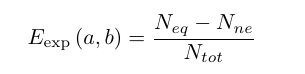
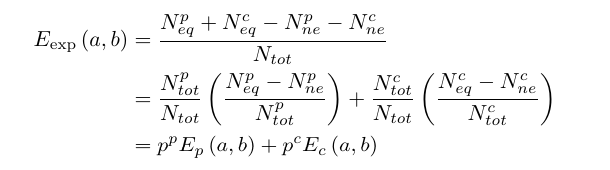
Jan-Åke Larsson
Please now recalculate the correlation from your model using your new-found formula
(that I tried to explain to you six months ago).
Best regards
Jan-Åke
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/CALLw9Yy%3DMXOA82kXG%3DO3Ag_grt734WL7DkCTB%2BW9XLUciAcm5g%40mail.gmail.com.
Jan-Åke Larsson
Professor, Head of Department
|
|
|
Department of Electrical Engineering SE-581 83 Linköping Phone: +46 (0)13-28 14 68 Mobile: +46 (0)13-28 14 68 Visiting address: Campus Valla, House B, Entr 27, 3A:512 Please visit us at www.liu.se |
Bryan Sanctuary

Jan-Åke Larsson
And the other correlations?
/JÅ
Bryan Sanctuary



Jan-Åke Larsson
In the previous manuscripts you claim you can (must) add the two correlations. In fact, your claimed violation of the inequality depended on that.
Now you have accepted that a correlation obtained from two subensembles is the weighted average of the two correlations of the subensembles. The data you had in your previous manuscripts does not violate the inequality when combined through the weighted average.
I don't know how you generate the numbers you just quoted to me.
Please rewrite all of this into a single, well-explained, derivation.
If you want to convince us, this is what you need to do.
Best regards
Jan-Åke
Mark Hadley
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/bbf709fd-ca1c-5451-5859-6ca22992887e%40liu.se.
Bryan Sanctuary
Bryan Sanctuary
Let's try to do this in small steps.Do you have an equation just forN_+ /N _tot at A for a polariser angle a
So that is the fraction of up readings measured at Alice for any particular angle aQM gives all these fractions but without any explanation. I think you are claiming to explain it with your parameter theta. By the way, I suggest that you give it another letter, say lambda, to distinguish it from polariser angles.
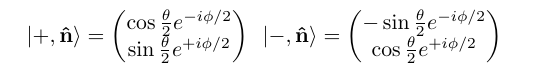
As a matter of fact, your parameter theta, that has explanatory power in an EPR type experiment, is called a hidden variable. That's what all other scientists mean by hidden variables. Your challenge is hard enough without trying to use a different language. So I suggest that as an edit.
Richard Gill
https://www.preprints.org/manuscript/202302.0055/v1
In the previous manuscripts you claim you can (must) add the two correlations. In fact, your claimed violation of the inequality depended on that.
Now you have accepted that a correlation obtained from two subensembles is the weighted average of the two correlations of the subensembles. The data you had in your previous manuscripts does not violate the inequality when combined through the weighted average.
I don't know how you generate the numbers you just quoted to me.
Please rewrite all of this into a single, well-explained, derivation.
If you want to convince us, this is what you need to do.
Best regards
Jan-Åke
On 2023-02-26 14:55, Bryan Sanctuary wrote:
Hi Jan-Åke
I have the papers up but they do not reflect this new point that has puzzled me for the last couple of months. Here is a draft of the new part, and the links are at the end
Bryan
<image.png>
<image.png>
On Sun, Feb 26, 2023 at 8:13 AM Jan-Åke Larsson <jan-ake...@liu.se> wrote:
Can you repost the link to your paper, I can't seem to find it anymore.
And the other correlations?
/JÅ
On 2023-02-26 13:12, Bryan Sanctuary wrote:
Dear Jan-Åke
Thanks for your question:
<image.png>
Bryan
On Sun, Feb 26, 2023 at 4:53 AM Jan-Åke Larsson <jan-ake...@liu.se> wrote:
Dear Bryan,
Please now recalculate the correlation from your model using your new-found formula
(that I tried to explain to you six months ago).
Best regards
Jan-Åke
On 2023-02-26 10:34, Bryan Sanctuary wrote:
Hi Richard
I hope I am not including uninterested people.
With Mark's expression, I can now unequivocally answer your insistence that I must average my two complementary contributions by dividing them by two. Here are the experimental clicks
<image.png>
which show the apparent violation of BI. Here are the same clicks rearranged to distinguish polarization from coherence
<image.png>
The two equations give exactly the same result, showing my approach is consistent with experiment, and your objection is answered.
This shows, BTW, that Bell's theorem has no relevance to qm. Non-locality plays no role in the violation. The apparent violation means that Nature obeys local realism.
Bryan
On Fri, Feb 24, 2023 at 5:55 AM Richard Gill <gill...@gmail.com> wrote:
Dear Bryan
So this is the formula now:
Jan-Åke Larsson
You say "the two contributions each do not violate BI giving respectively 2 and 1." In one of your manuscripts, you claim a violation with the value 3 by adding them together. This does not happen if you do a weighted average.
If the first contribution is for the fraction p_c of all events and the second contribution the fraction p_s of all events, then p_c+p_s=1 (if there are no other contributions). Then the weighted average
2*p_c+1*p_s <= 2
So no violation for any size of the fraction from the first contribution.
Best
Jan-Åke
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/CALLw9Yx5-6rZ4NwwmC1J-FQ6yiQ2zXX7Var_GBR6s_QRoDLyVw%40mail.gmail.com.
Richard Gill
On 26 Feb 2023, at 18:19, Mark Hadley <drmark...@gmail.com> wrote:
Dear Bryan,Your answer was incomprehensible. I have less idea than ever about what you are claiming. Much less whether you are correct.I thought you were going to explain the predictions of QM and violation of bells inequalities with a local realist theory. That was the bet as I understood it. To do that you need a theory that predicts measurement results and then we can check the correlations.QM already correctly predicts correlation distributions. It does so without anything spooky like non local signals. It is self consistent. An underlying explanation in terms of individual results is elusive and problematic.CheersMark
On Sun, 26 Feb 2023, 17:43 Bryan Sanctuary, <bryancs...@gmail.com> wrote:
Hi MarkI answer below:
Let's try to do this in small steps.Do you have an equation just forN_+ /N _tot at A for a polariser angle aIn my simulation, I generated clicks as coincidences, so I only got the coincidence probabilities N_(+-)/N_tot etc. .The program could be modified to extract the individual ratios and then combine them. I will eventually do that but it was unnecessary for the simulation of the correlations. If you look at the code you will see how I did it in terms of coincidences.So that is the fraction of up readings measured at Alice for any particular angle aQM gives all these fractions but without any explanation. I think you are claiming to explain it with your parameter theta. By the way, I suggest that you give it another letter, say lambda, to distinguish it from polariser angles.The only variable is the local value of theta which is used by everyone to define the states (Greenberger, D. M., Horne, M. A., Shimony, A., & Zeilinger, A. (1990). Bell’s theorem without inequalities. American Journal of Physics, 58(12), 1131-1143.) See equations A2,
<image.png>
My work is very much not about Bell's theorem and it would be confusing to change that theta to lambda. Hidden variables mysteriously complete the wave function, and mine needs no completion. They are simply different orientations on the Bloch sphere. Alice and Bob are correlated by a common theta at the source.As a matter of fact, your parameter theta, that has explanatory power in an EPR type experiment, is called a hidden variable. That's what all other scientists mean by hidden variables. Your challenge is hard enough without trying to use a different language. So I suggest that as an edit.Exactly, and I have done just that, but without any hidden variables. I am using the language of standard QM and not the language that Bell used simply because that leads to the wrong conclusion and misleading confusion in his theorem. Bell says that the only way to account for the violation is with non-locality. This statement by Bell is now incorrect:"If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."I hope this is getting clearer to you all. It is not easy to change 60 years of Bell's misconceptions.I very much appreciate your comments and interest. It is a daunting task, I agree. One gobsmacking consequence of this is the idea of Dirac that predicts a matter-antimatter pair is replaced with a single particle with two axes of quantization. Think of the consequences that hole theory and sea of electrons is replaced by one particle in the Dirac field, not two particles with two states each.Bryan
CheersMark
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/bbf709fd-ca1c-5451-5859-6ca22992887e%40liu.se.
Inge Svein Helland
Dear Bryan,
I have printed out your 3 articles, and have had a brief look at them. Please tell me if I have misunderstood you, but my current understanding is as follows: You have constructed a formalism, generalizing Dirac's formalism, in which you can befine a property called hyperhelicity. Using this variable and this formalism, you claim that the usual spin components are not necessarily +1 and -1, and thus the argument behind the CHSH inequality breaks down.
As I see it, the statement that the spin components are +1 or -1 is not connected to any formalism, but to an experiment, the Stern-Gerlach experiment, which can be performed by either Alice or Bob, and has two possible outcomes. Just by conventon these can be called +1 and -1.
The question for me is: Can the hyperhelicity be measured in any way, by any experiment, by any observer? If not, it is just an inaccessible, hidden variable, in the same way as the unit spin vector n (I drop the hat in this e-mail). Note that the spin component in direction a can be defined in terms of this n, just take sign(cos(a,n)).
These spin components are accessible. To me, the distinction between accessible and inaccessible variables is the important one.
Is your hyperhelicity accessible?
Inge
Sent: 26 February 2023 18:26:29
To: Mark Hadley
Cc: Bryan Sanctuary; Mark Hadley; Jan-Åke Larsson; Chantal Roth; Bell Inequalities and quantum foundations
Subject: Re: [Bell_quantum_foundations] Re: Local hidden variables.
Алексей Никулов
Dear Richard, Zeilinger, Gisin and the like really should retract their papers, which are based on the mass delusion that quantum mechanics predicts
the EPR correlation and violation of Bell inequalities.
With best wishes,
Alexey
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/011fb5de28df411da1fb5b959c270cb1%40math.uio.no.
Richard Gill
On 27 Feb 2023, at 17:05, Алексей Никулов <nikulo...@gmail.com> wrote:
Mark Hadley
Алексей Никулов
Dear Richard,
Zeilinger, Gisin and the like claim in their papers that quantum mechanics predicts the EPR correlation and violation of Bell’s
inequalities. Bell proposed his inequalities in order to prove that hidden variables theory cannot predict violation of these inequalities
in contrast to quantum mechanics. Therefore, if quantum mechanics does not predict the violation of Bell's inequalities, then Bell's
inequalities do not make any sense. Bell's inequalities do not make any sense, especially if such an absurd as the EPR correlation
postulated by Bohm in 1951 is really observed in the laboratory. Bohm postulated that the mind of Alice can create the spin state of not
only her particle but also the spin state of Bob’s particle. Quantum mechanics can predict the EPR correlation only if this absurd was
postulated. With best wishes,
Alexey
anton vrba

Jan-Åke Larsson
 Yes, I predict superluminal communication as possible!
Yes, I predict superluminal communication as possible!
/Jan-Åke
anton vrba
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.
Richard Gill
anton vrba
No it doesnt. The |H_1V_2> quantum state is not a total spin zero state. Noether's theorem does not apply.
/Jan-Åke
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/em0f22bfe5-c938-4542-bf86-147d72a1cb26%40a3b55c15.com.
Jan-Åke Larsson
/Jan-Åke
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/em0f22bfe5-c938-4542-bf86-147d72a1cb26%40a3b55c15.com.
Richard Gill
On 27 Feb 2023, at 20:35, anton vrba <anto...@gmail.com> wrote:
Let's agree to disagree. In my paper https://neophysics.org/p/1805) I explain how I arrived at my conclusion.------ Original Message ------From "Jan-Åke Larsson" <jan-ake...@liu.se>To "anton vrba" <anto...@gmail.com>Date 2/27/2023 7:31:13 PMSubject Re: [Bell_quantum_foundations] Let's remove Bell from experiments that demonstrate entanglement
No it doesnt. The |H_1V_2> quantum state is not a total spin zero state. Noether's theorem does not apply.
/Jan-Åke
On 2023-02-27 20:26, anton vrba wrote:
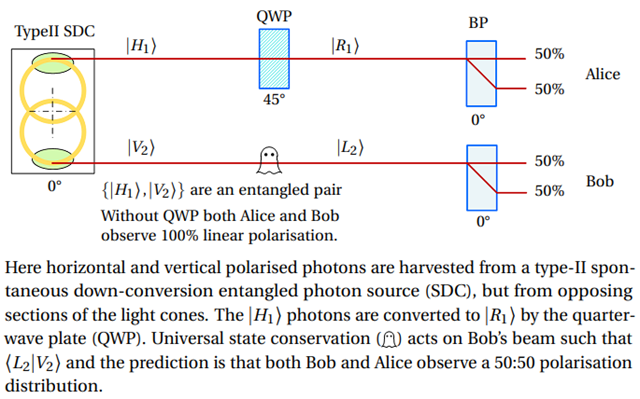
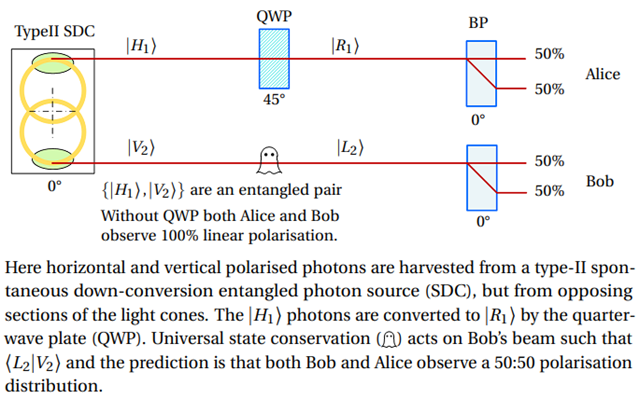
But Jan, Noether theorem requires that when the QWP is inserted in Alice's path and produces a right-circularly polarised photon the Bob's entangled photon must change to a left-circularly polarised photon to preserve the zero spin state before and after the QWP. Anything else and you are breaking conservation laws --- think about it.
RegardsAnton
------ Original Message ------From "'Jan-Åke Larsson' via Bell inequalities and quantum foundations" < Bell_quantum...@googlegroups.com>To "anton vrba" <anto...@gmail.com>; "Bell Inequalities and quantum foundations" < bell_quantum...@googlegroups.com>Date 2/27/2023 7:08:16 PMSubject Re: [Bell_quantum_foundations] Let's remove Bell from experiments that demonstrate entanglement
On 2023-02-27 20:02, anton vrba wrote:
<w0beixs4.png>
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/em112fd2ee-7ef9-4112-8323-5af8867a52cf%40a3b55c15.com.
Richard Gill
On 27 Feb 2023, at 20:39, Richard Gill <gill...@gmail.com> wrote:
I agree with Jan-Åke. You said, Anton, that the photons are initially in a Bell entangled state.
Jan-Åke Larsson
Eberhard, Phillippe H.; Ross, Ronald R. (1989), "Quantum field theory cannot provide faster than light communication", Foundations of Physics Letters, 2 (2): 127–149, https://doi.org/10.1007%2FBF00696109
/Jan-Åke
Jan-Åke Larsson
(And neither would using an entangled state.)
/JÅ
Bryan Sanctuary
Inge Svein Helland
Dear Bryan,
Thank you very much for your clarification. I am trying to understand.
So you look upon hyper-helicity as a part of reality, but at the same time beyond our capacity to measure. In some way this may seem to contradict Hervé Zwirn's Convivial Solipsism, which says that every description of reality should be relative to the mind of some observer. But may be there is no contradiction if we include the words 'description of'. Your papers aim at a desciption of hyper-helicity.
In your discussion with Jan-Åke, you describe the experimental Bell correlation as a linear combination of the contribution from polarisation and the contribution from coherence. The latter you say to me is generated from hyper-helicity, that is beyond our ability to measure.
So part of your message is linked to our limited ability. I have a similar message in my paper on the Bell experiment, which I attach here. Maybe our two views can be united in some way?
(There is a serious misprint in my paper: In (ii) in Theorem 1 'irreducible' should be replaced by 'reducible'. In the finite-dimansional case, by letting G be the cyclic group, and U a suitable reducible representation, this point can be automatically fulfilled.)
Inge
Sent: 27 February 2023 20:56:56
To: Inge Svein Helland
Cc: Richard Gill; Mark Hadley; Mark Hadley; Jan-Åke Larsson; Chantal Roth; Bell Inequalities and quantum foundations
anton vrba

Jan-Åke Larsson
Dear Jan-Åke and Richard,
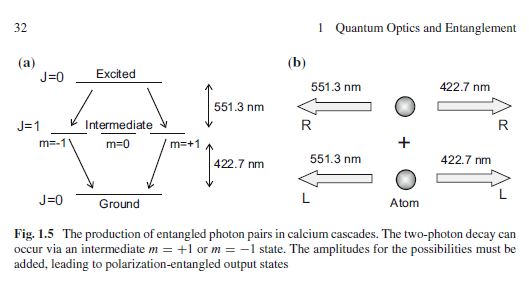
The 1972 Freedman Clauser experiment used a calcium light source that produced 2 circularly polarised photons as explained
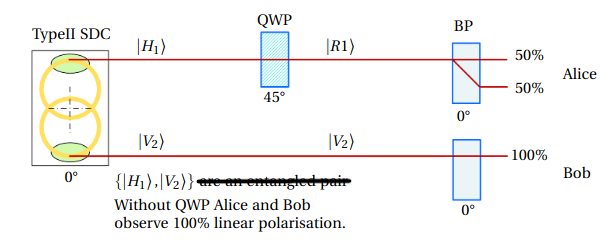
But I'll discuss the Freedman and Clauser if you want. They generate the entangled state |R1 R2>+|L1 L2>=|H1H2>-|V1V2>.
[Simon, D.S., Jaeger, G. and Sergienko, A.V. (n.d.) Quantum Metrology, Imaging, and Communication.] who writes"The excited electron can decay in two steps, via this intermediate state. Two photons are emitted in the process. These photons may be emitted in any direction, but if we look only at photons emitted back-to-back, i.e. look at coincidence counts from detectors separated by 180◦, then angular momentum conservation requires the two photons to have the same circular polarization (left-handed or right-handed)." In other words the two photon production is nilpotent and the two photons are entangled to preserve the nilpotency. I do not like the plus sign in the figure because both sets of photons are not produced simultaneously, it is either R or L but not R+L.
The individual photons are not in either R or L, they do not, as individual particles, have a definite polarization. If they did, this would not be a total-spin zero state.
We know from Freedman and Clauser that Alice receives a circularly polarised photon (either L or R) and converts it to a linearly polarised photon. The helicity, or spin, L or R does not influence polarisation direction probability which is 50:50. The action of polarisation by Alice has to be a nilpotent event, (the wave function collapse ensures this nilpotency) hence Bob photon is polarised oppositely before Bob observes it, hence the correlations.
If both Alice and Bob measures circular polarization they get random outcomes (that are equal).
If Alice measures horizontal/vertical polarization and Bob measures circular polarization they get random outcomes (that are independent).
There is no communication.
Here we are dealing with photons that have quantum properties spin, energy=hf, polarisation and orbital momentum, the later not being considered here (and there are no hidden variables as Bryan and others want to claim). Physics explains the entanglement by the collapse of a wave function and gives no further reason why. I am investigating the why and postulating a preservation phenomenon demanded by Noether's theorem, which was invoked to explain the properties of the photons produced by the calcium light source, and why should it not continue to apply during the flight time of the two photons?
Momentum is preserved in a billiard ball collision. If you later bounce one of the billiard balls off something hard, the total momentum of the two billiard balls is not conserved. And the second billiard ball is unaffected.
Total spin is preserved in a calcium cascade emission. If you later change the spin of one of the photons, the total spin is not conserved. And the second photon is unaffected.
Now to Kwiat et al (DOI: 10.1103/PhysRevLett.75.4337) and all modern EPR-Bell experiments use spontaneous down conversion crystals. Similar to the two photon production of atomic cascades, the two photon production in down conversion crystals also has to be nilpotent, hence the two photons produced similarly are entangled as the photons of the calcium light source. The harvesting of photons at the intersection does not ensure entanglement, it only satisfies the Bell theorem requirement of not knowing, i.e. an either or selection. I say lets know and prove entanglement as a nilpotent requirement without invoking Bell. Looking at the below progression of light cone development of type II down conversion crystals we can harvest entangled photons with known polarisation very efficiently in (e), these photons were produced by a nilpotent down conversion process and are entangled to ensure future nilpotent actions, just as the calcium light source used by Freedman and Clauser. Please explain to me why physics decided that entanglement can only be at the intersection of the two light cones and not elsewhere.
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/ema3bf3132-d8c7-4c22-ad6b-a84fd7d20f3f%4099ab69bb.com.
anton vrba
On 2023-02-28 13:49, anton vrba wrote:
This is not your proposal. Your proposal generates the product state |H1 V2>. That is the picture you sent.Dear Jan-Åke and Richard,
The 1972 Freedman Clauser experiment used a calcium light source that produced 2 circularly polarised photons as explained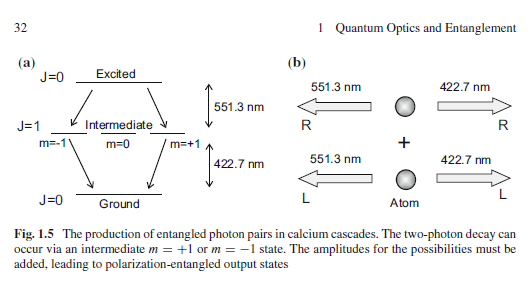
But I'll discuss the Freedman and Clauser if you want. They generate the entangled state |R1 R2>+|L1 L2>=|H1H2>-|V1V2>.
[Simon, D.S., Jaeger, G. and Sergienko, A.V. (n.d.) Quantum Metrology, Imaging, and Communication .] who writes
Jan-Åke Larsson
I am responding with the actual quantum-mechanical behavior.
You are claiming the wrong behavior in Figure 3. There will be no "ghostly action at a distance" there.
This will happen:
And in Figure 1 Bob will have 50/50 distribution no matter what Alice does.
Again, sorry to disappoint you.
Best
Jan-Åke
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/em000b9ce9-f517-4ded-8402-124d1ea84769%4099ab69bb.com.
anton vrba
Jan-Åke Larsson
It is not the Copenhagen interpretation I am using. This is a straight QM calculation of probabilities. Even when using Bohmian mechanics, these predictions remain. Your Figure 3 claims a behavior that does not occur.
It is probably the case that an event-by-event description using Bohmian mechanics and a proper EPR state as in your Figure 1 has an explicit action at a distance, but the overall statistical behavior remains: Whatever Alice does to her system, Bob will see a 50/50 distribution of the outcomes. Even in Bohmian mechanics, there is no change to Bob's statistical output. Even in Bohmian mechanics there is no superluminal communication.
Besides, the experiment you are proposing is made every time a fibre-optic Bell-experiment setup is calibrated. Two fixed plane-polarization beams of light are used to determine the polarization rotation of the channel (which drifts slowly as the optical fibres expand and contract with temperature as it changes during the day). The effect you propose is not seen.
Also, if you read the supplementary material for the 2015 experiments from Vienna and NIST we do check that there are no such explicitly nonlocal effects in the Bell experiment data. The local distribution at Bob remains at 50/50 whatever is the measurement setting at Alice.
If it worked like you propose, we would already be using technology based on that effect in our optical networks. Despite what you might think experimenters, or even <cough> theorists, are not stupid.
Best regards
Jan-Åke
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/embe8055e3-47f1-4343-8aac-2cc168b3fe00%4099ab69bb.com.
Mark Hadley
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/embe8055e3-47f1-4343-8aac-2cc168b3fe00%4099ab69bb.com.
Алексей Никулов
Dear Mark, Your statement “The mind of Alice is not part of any QM calculation” is extremely naive. Indeed the mind of Alice, Bob or any other
observer cannot be part of any calculation, since an influence of the mind on the state of the observed system is impossible not only to
calculate, but even to imagine. But this does not mean that quantum mechanics can describe some quantum phenomena, for example,
the Stern-Gerlach effect without the influence of the observer's mind on the state of the quantum system. I hope you know that each non-entangled spin state is an eigenstate in one direction and superposition of states in any other direction of
the real three-dimensional space. For example,
|+>_{z1} = cos f/2 |+>_{z2} + sin f/2 |->{z2} (1)
is the eigenstate along the z1 axis and superposition of state along the z2 axis, f is the angle between z1 and z2. This state jumps into the
eigenstate along the z2 axis and superposition of state along the z1 axis |+>_{z2} = cos f/2 |+>_{z1} - sin f/2 |->{z1} (2)
when Alice sees with the probability |cos f/2|^2 that the particle deviated upwards along the z2 axis.
What other than the mind of Alice could change the spin state of the particle?
With entangled spin states, it is even more absurd. Spin states of particles A and B of the EPR pair|EPR> = (|A+,B-> + |A-,B+>)/2^0.5 (3)
cannot exist before the first observation one of the particles. The first observation of spin projection in any direction of any particles will
give spin up |+> with the same probability 0.5 in contrast to non-entangled particles (1) or (2) having spin state.
Jan-Åke understands that “The individual photons are not in either R or L, they do not, as individual particles, have a definite
polarization”, see his last letter to Anton. But for some reason he does not understand that it is completely absurd when the physical
theory postulates that the mind of the observer can create a quantum state during observation. Einstein understood that this is absurd.
Therefore, he said “I like to think that the moon is there even if I don't look at it” explaining his negative attitude to quantum mechanics.
The absurdity in the understanding of quantum mechanics has only increased over time. If, according to the Dirac jump postulated in
1930, the mind of the observer can create a state only of the observed particle, then Bohm in 1951 expanded the omnipotence of the
mind by postulating that the mind can create the states of both particles of the EPR pair, regardless of the distance between them,
observing only one particle. Quantum mechanics cannot predict the EPR correlation and violation of Bell’s inequalities without this
omnipotence of the mind postulated by Bohm.
John Bell said in his talk 1989 “Against 'measurement'” about N.G. van Kampen: “He dismisses out of hand the notion of von
Neumann, Pauli, Wigner — that 'measurement' might be complete only in the mind of the observer”. Most people cannot understand
that quantum mechanics is an absurd theory since they, like N.G. van Kampen, dismisses out of hand the notion of von Neumann,
Pauli, Wigner — that 'measurement' might be complete only in the mind of the observer. With best wishes,
Alexey
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/5fbf205446c24f50b6445c44f73bd427%40math.uio.no.
Mark Hadley
Алексей Никулов
Dear Richard, I understand perfectly well that most people nowadays understand under “quantum mechanics” what that has nothing to do with
quantum mechanics. A catastrophic regression of physical thinking is observed now. The reason for this regression is the rejection of
realism by the creators of quantum mechanics because of their false confidence that we can explain any phenomena. The same false
confidence is evident in your question “How can I explain violation of Bell inequalities?” Before trying to explain the violation of the
Bell inequalities or the EPR correlation, if they are observed, it is necessary to explain the Stern-Gerlach effect, without the trick with
‘observation’ or ‘measurement’. So far, no one has managed to do this.
You understand that Bell inequalities are derived under the assumption of local hidden variables. But you do not understand that no
theory of hidden variables is possible without the trick with ‘measurement’. Therefore, you cannot understand that Bell's inequalities,
at best, can only prove that the trick with ‘measurement’ cannot be successful, since the measurement is local, and it is necessary to use
the trick with ‘observation’ that is non-local. But those who really understood quantum theory, such as Einstein and Schrodinger, and
without Bell's inequalities, knew that the trick with ‘observation’ cannot be replaced by a trick with ‘measurement’.
With best wishes,
Alexey
GeraldoAlexandreBarbosa
Dear Anton “vrba”,
I just saw your comment to Jan-Åke and Richard. I would like to comment the following points on your email:
1. “I do not like the plus sign in the figure because both sets of photons are not produced simultaneously, it is either R or L but not R+L”.
First, let me restrict my comments to photons. Simultaneity can be theoretically defined but, experimentally, there is a subtlety: If the experimental conditions are such that two events happen within the same time window, they are “simultaneous”. If this time window is reduced continuously and the coincidences are still there, the events are simultaneous, up to that measured condition. Yes, it is a pragmatic definition, but difficult to bypass.
2. “The harvesting of photons at the intersection does not ensure entanglement, it only satisfies the Bell theorem requirement of not knowing, i.e. an either or selection”.
Again, what is called an “intersection” in this case, it is also tied up to the experimental conditions. Photons birthplace in a crystal cannot be defined better than the focused region of the laser beam creating them. This means a position uncertainty – and a momentum one as well. If they cannot be separated, by a time or space filter, harvesting happens in an entanglement condition.
Furthermore, the indistinguishability condition for two photons it is identical to say that the photons are optically coherent. [PRA vol 47, No 3, 2293 (1993)]
3. “Please explain to me why physics decided that entanglement can only be at the intersection of the two light cones and not elsewhere. That is delusional and inconsistent! “
It is my understanding that you are talking about Type II down-conversion, where two distinct cones are created, each cone with a given polarization. At the cone intersection, the wave stated can be written as an entangled polarization state (under the condition of position indistinguishability of the two photons), but not at any other point. Twin photons can also be entangled in momentum in other places that satisfy phase matching conditions, but polarization entanglement, only happens at the crossing of the two cones. [see Fig. 1 on PRA 80, 063833 (2009), that discuss the wave state. For the phase matching for all crystal classes, see PRA vol 76, 033821 (2007)].
What is also true and puzzling is that, differently from Type I down-conversion, Type II only allows PARTIAL total momentum conservation (from laser to down-converted photons. This is derived in PRL 85, No 2, 286 (2000). Basically, Type II down-conversion does not have azimuthal symmetry along the laser beam – that is a condition for total angular momentum conservation.
The implications of non-conservation of momentum are yet to be fully understood.
Regards,
Geraldo
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/ema3bf3132-d8c7-4c22-ad6b-a84fd7d20f3f%4099ab69bb.com.
Inge Svein Helland
Dear Bryan, dear Richard, dear all (and dear Alexey, sorry, I think your model is too simple).
I am trying to understand your model, Bryan, and I am trying to understand the bet between you and Richard. As I see it, the discussion should not be about the mathematics, which you have clarified to me, at least to a sufficient degree, but about the simple statement:
Hyper-helicity is an element of reality.
To me, this statement is not very different from the statement:
The spin vector n(hat) is an element of reality.
So let us for simplicity start with the last statement. I see quantum mechanics as a model, but a good model of reality. In this model, the spin vector has no place, only the component in some fixed, chosen direction. A model where the spin vector does have a place, is a model where we can draw this spin vector, and in a geometric figure draw its component. I think that this model is simply too simple, it cannot explain several real phenomena.
Then go back to hyper-helicity. It has no place in the ordinary quantum model, in the version due to Dirac, where SU(2) is the basic symmetry group. It can be defined in Bryan's model, where SU(2) is replaced by quaternian symmetry. So, similar to the spin vector case, it is a question which model should be chosen. In my opinion, and I think this opinion is shared by Richard, ordinary quantum mechanics is a good enough model, it can explain most of the phenomena that we know of.
Bryan, what you have to convince us about, is that your model is a better model, it can explain more real phenomena. I think that 'reality' is a too big and complicated notion, and so is 'element of reality'. It is all connected to our models, and which model to choose.
In my own papers I try to argue that a simpler version of of the quantum model is sufficient to explain most phenomena: Let the state notion be limited to ket vectors that are eigenvectors of some Hermitean operator. In my published paper 'On Reconstructing parts of quantum theory from two related maximal conceptual variables' ( paper for which a technical correction note will appear soon), I have argued that in this model version, 'paradoxes' like the Schrödinger cat paradox are avoided. It also leads to a simple interpretation of state vectors: They are in one-to-one correspondence with a question: 'What is theta?/what will theta be if we measure it?' together with a sharp answer 'theta=u'. Here theta is a maximal accessible variable taking a discrete set of values. It is connected to the physical world in some given context, but it may also be connected to the mind of an observer or to the joint minds of a group of communicating observers.
If the variable is not maximal, the same interpretation can be given to the eigenspaces of the relevant operator.
So to my main point: It is not a question of reality or not reality, it is a question about which model we use to describe reality. Some models are too simple; some models may be too sophisticated.
This is my view.
Inge
Sent: 28 February 2023 18:34:17
To: Richard Gill
Cc: Bryan Sanctuary; Inge Svein Helland; Mark Hadley; Jan-Åke Larsson; Chantal Roth; Bell Inequalities and quantum foundations; Mark Hadley
Austin Fearnley
There have been some stimulating recent comments on this thread, especially from Inge and Geraldo.
Quote from Inge:
"In my own papers I try to argue that a simpler version of of the quantum model is sufficient to explain most phenomena: Let the state notion be limited to ket vectors that are eigenvectors of some Hermitean operator. In my published paper 'On Reconstructing parts of quantum theory from two related maximal conceptual variables' ( paper for which a technical correction note will appear soon), I have argued that in this model version, 'paradoxes' like the Schrödinger cat paradox are avoided. It also leads to a simple interpretation of state vectors: They are in one-to-one correspondence with a question: 'What is theta?/what will theta be if we measure it?' together with a sharp answer 'theta=u'. Here theta is a maximal accessible variable taking a discrete set of values. It is connected to the physical world in some given context, but it may also be connected to the mind of an observer or to the joint minds of a group of communicating observers."
I believe that I caused Mark, in an older thread to cut short his comments as I was taking the ridiculous stance of denying superposition of states. I accept the power of statistics in very usefully manipulating the distributions of multi-particle states, but that is not the same as believing the particles actually possess indeterminate individual states until a measurement is made. An analogy is a class of candidates' examination marks about to be announced to the candidates. Before the announcement, the list of marks is in a superposition or entangled state in the minds of the candidates. After the announcement each candidate has their own 'sharp' answer or 'theta = say 75%'. The candidates' minds played no part at the instant of announcement and there was no superposition in actuality. One can perform fancy calculations on the distribution of the classes' marks, and even make predictions about the contributions to the school's performance in government league tables. The distributions may be very useful but there is no actual superposition in those marks.
Inge wrote that his own model avoided the Schrodinger's cat paradox. That paradox can be avoided using the Russian Dolls analogy but it is also avoided if one denies the actuality of superposition. Superposition of two particle spins supposed to be indeterminate before measurement is the micro version of the macro paradox of Schrodinger's cat. Again, retrocausality removes entanglement and superposition from a simple version of a Bell experiment simulation.
Inge also wrote about complexities of models and I will write about that soon.
Austin
Inge Svein Helland
Dear Austin,
Thank you for your comments. Just a brief response here; I can response in more detail later when you take up my more general issue on the complexity of models.
I do not in any way deny the superposition of states, but I do not think that all superpositions lead to meaningful state vectors. I want to concentrate on state vectors that are eigenvectors of some meaningful operator, and I think that this is enough in most context.
Take entanglement, for instance. The ordinary singlet vector is an eigenvector of the operator determined by the variable in the 4-dimensional Hilbertspace n_A dot n_B, where n_A is the spin vector of Alice's particle, and n_B is the spin vector of Bob's particle. These spin vectors are inaccessible to any observer, but the dot product is accessible to an observer Charlie, which tries to model the results of Alice and Bob. Specifically, this operator has the eigenvalues -1 and -3, and Charlie is in the eigenstate corresponding to the eigenvalue -1, which implies that to him, the response of Bob in any fixed direction must be opposite to the response of Alice on the same direction.
I look forward to your further comments.
Inge
Sent: 01 March 2023 12:15:51
To: Bell inequalities and quantum foundations
Subject: Re: [Bell_quantum_foundations] Re: Local hidden variables.
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.
Inge Svein Helland
Dear Austin again,
For a reference to the concrete results that I gave for the singlet vector, and a further discussion, see Leonard Susskind and Art Friedman (2014). Quantum Mechanics. The Theoretical Minimum, pp. 163-181, in particular Exercise 6.9, p.181.
Inge
Sent: 01 March 2023 12:50:32
To: Austin Fearnley; Bell inequalities and quantum foundations
Алексей Никулов
I have answered your question. But you don't want to understand the
answer. The statistics of Bell's experiments by themselves do not
make sense. Bell's experiments would have been impossible without the
inexplicable paradox of the Stern-Gerlach effect. J. von Neumann has
proved in 1932 with his no-go theorem the impossibility to describe
binary outcome of the Stern-Gerlach effect without the trick with
‘observation’. Bell claimed in his first paper [2], published after
his second famous paper [3], that the proof of von Neumann is false.
Twenty - two years later, Bell said: “The proof of von Neumann is not
merely false but foolish!”, see the paper of David Mermin [4].
Bell and also Mermin [4] were sure that the proof of von Neumann is
false and even foolish, since von Neumann allegedly did not take into
account that to describe the Stern-Gerlach effect, we can use a trick
with ‘measurement’ that does not contradict realism, and not use a
trick with ‘observation’ that contradicts realism. The trick with
‘measurement’ is needed since variables cannot be hidden without this
trick. You should understand that the trick with ‘measurement’ used in
the theory of hidden variables is not fundamentally different from the
trick with ‘observation’ used in quantum mechanics. In both cases, all
the difficulties that do not allow us to describe the phenomenon as a
manifestation of reality are hidden in the process of ‘measurement’ or
‘observation’.
Since both processes cannot be described, the requirement of locality
is the only way to distinguish the trick with ‘observation’ from the
trick with ‘measurement’. Bell used this requirement in his famous
paper [3] following Einstein, Podolsky and Rosen. Bell said that “The
proof of von Neumann is not merely false but foolish!” since this
requirement is absent in the proof of von Neumann. Bell was wrong not
only because the trick with ‘measurement’ is not fundamentally
different from the trick with ‘observation’, but also because von
Neumann belonged to those few who understood that the trick with
‘observation’ cannot be replaced by a trick with ‘measurement’. Bell
himself said about this in 1989: “He dismisses out of hand the notion
of von Neumann, Pauli, Wigner - that 'measurement' might be complete
only in the mind of the observer” [5]. The ‘measurement' which might
be complete only in the mind of the observer is observation.
The whole story of Bell's inequalities became possible because of the
desire of most scientists to create and maintain the illusion that we
can explain all the phenomena that we observe. Bohm was able to
mislead Bell because Bell had the illusion that quantum mechanics,
which is absurd, can be replaced by a theory of hidden variables,
which is less absurd. This desire to create the illusion is observed
up to now. Mark follows the illusion that Decoherence is the answer.
Inge believes even in Qbism and convivial solipsism. The most
unthinkable fantasies are published, the authors of which do not seem
to be able to think critically at all. Worst of all, critical articles
are banned by the censorship of believers in quantum mechanics. These
unthinkable fantasies and this censorship result in the degradation
of physical thinking.
[1] J. von Neumann, Mathematical Foundations of Quantum Mechanics.
Princeton, NJ: Princeton University Press (1955); Mathematishe
Grundlagen der Quantem-mechanik. Springer, Berlin (1932).
[2] J.S. Bell, On the problem of hidden variables in quantum
mechanics. Rev.Mod. Phys. 38, 447-452 (1966).
[3] J.S. Bell, On the Einstein-Podolsky-Rosen paradox. Physics 1,
195-200 (1964).
[4] N.D. Mermin, Hidden variables and the two theorems of John Bell.
Rev. Mod. Phys. 65, 803-815 (1993).
[5] J. S. Bell, Against Measurement. in the proceedings of 62Years of
Uncertainty. Plenum Publishing, New York 1989; Physics World 3, 33-40
(1990).
With best wishes,
Alexey
ср, 1 мар. 2023 г. в 16:57, Inge Svein Helland <in...@math.uio.no>:
Richard Gill
You give me no answer.
Except that you say “The whole story of Bell's inequalities became possible because of the desire of most scientists to create and maintain the illusion that we can explain all the phenomena that we observe.”
So you say that there is no explanatation for the results of the experiments in which violation of Bell inequalities is observed. You have no explanation. You are not interested in looking for an explanation.
Or do you claim that the results were falsified? It is all a huge conspiracy?
I find your attitude anti-scientific.
Richard
Sent from my iPhone
>
> Dear Richard,
Алексей Никулов
I try to explain to you that any attempts to explain the violation of
Bell inequalities are meaningless until an explanation of the
Stern-Gerlach effect without the trick with ‘observation’ or
‘measurement’. I don't think the Stern-Gerlach effect can be
explained. Understanding that our reason cannot explain everything is
not anti-scientific. The unreasonable belief that we can explain
everything is anti-scientific. This unfounded belief has led to the
mass delusion about quantum mechanics.
With best wishes,
Alexey
ср, 1 мар. 2023 г. в 19:21, Richard Gill <gill...@gmail.com>:
Austin Fearnley
Thank you for the comments and reference. I do not have Susskind and Friedman but I did follow all of Susskind's free online courses in the "Theoretical Minimum" series including one on Quantum Mechanics and one on entanglement. I had previously bought the book 'quantum mechanics for idiots' but Susskind's courses were much easier to understand!
So back to my comments on complexities of models. You wrote that Alexei's model was too simple. I am not clear what Alexei's model is. I agree with the spirit of Alexei's unwillingness to accept QM for whatever (mistaken?) reasons he has. I agree because of the probable knock-on effect on QM of my retrocausal model. It eschews entanglement because separate particles in a simple Bell simulation always have separate states, though those states might be identical. Alexei seems to be denying entanglement yet, despite my reading all his posts, I am not sure that he has explicitly written that.
Inge wrote:
"... I see quantum mechanics as a model, but a good model of reality. In this model, the spin vector has no place, only the component in some fixed, chosen direction. A model where the spin vector does have a place, is a model where we can draw this spin vector, and in a geometric figure draw its component. I think that this model is simply too simple, it cannot explain several real phenomena.
Then go back to hyper-helicity. It has no place in the ordinary quantum model, in the version due to Dirac, where SU(2) is the basic symmetry group. It can be defined in Bryan's model, where SU(2) is replaced by quaternian symmetry. So, similar to the spin vector case, it is a question which model should be chosen. In my opinion, and I think this opinion is shared by Richard, ordinary quantum mechanics is a good enough model, it can explain most of the phenomena that we know of."
I started my work on Bell by helping Fred Deiter to try to obtain a computer program to show that Joy Christian's ('one page') model broke Bell's Theorem. I first started with hidden variables which were spin vectors represented by fixed-value vectors. I never managed to break Bell. That was one of my problems in devising a more complicated model as all models cannot break Bell (ask Richard!). How does one recognise a better model if all [local, hidden variable] models (must theoretically) fail to break Bell? I note that Bryan says he is not interested in Bell, and I have no doubt that his model will not break Bell. Yet his model may possibly have value when avoiding the Bell experiment.
At some point I (should have) realised that that the answer lay outside Bell and I became interested in Malus's Law. In fact, I just wearied of banging my head against the Bell and wanted to try something different. It seemed clear to me that a constant vector for polarisation could not be used to give the varying proportions found in Stern Gerlach measurements. So I tried a gyroscopic hidden variable with precession and nutation. That fitted the requirements for the electron and the photon. To conform with Malus's Law the gyroscope vector corresponding to polarisation |up> needs to point towards up more than it points at the horizon. So I reverse engineered the amount of nutation needed to give Malus's Law. I then wrote and published a computer program to give Stern Gerlach outcomes based on this model. (So I am not clear what Alexei means by the mystery of the Stern Gerlach outcomes?) So I had generated a 2-D probability envelope for the direction that the 'gyroscope' pointed at. I still have no mechanism to produce that probability envelope. For an electron the gyroscope points at the direction θ with probabiity 0.5*sin θ where for an |up> electron θ=90 degrees represents the 'gyroscope' pointing in the up direction. I have recently noted a Lamour precession may be relevant to calculating the probability envelope. Also Susskind (Entanglement online lecture 9) calculates the precession effect about the z axis if a constant magnetic field points along the z axis.
So, armed with my improved hidden variable model, I tried a Bell simulation with this model. Would the correlation be 0.707? (No, impossible) Would it be 0.5? (Alas, no)? It was approx 0.35.
Convinced that I had an improved model as it explained Stern Gerlach outcomes, I tried retrocausality of antiparticle behaviour and that worked very well. So well that the 200-year-old Malus Law was all that was necessary to perform the calculations calculations. The precession and nutation (the phase effects?) of individual particles were not required in the calculations as a large enough sample of particles conforms to the 0.5*sin θ probability envelope to give a correlation = 0.707. Retrocausality does not require entanglement and Bell's Theorem is bypassed rather than broken.
Austin
Inge Svein Helland
Dear Austin,
I will be busy today, but will try to answer you tomorrow.
Inge
Mark Hadley
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/CAKiL4iJCXfv8McOz6r0%2B8XQTKa0ah-Z9ztNX5oEsogJ2CJAynQ%40mail.gmail.com.
Inge Svein Helland
Dear Mark, dear Austin, dear all,
As a statistician I have worked for more than 10 years trying to understand the foundations of quantum mechanics. Now I seem to have reached some sort of a goal.
As I see it, QM is a model, and a good model in order to understand the world. It is concerned with our endeavor to achieve knowledge of the world. At the outset we can assume a physical context, some physical variables in this comntext, and an observer A. Then make the following 4 postulates:
Postulate 1: Every physical variable in this context has a paralell existence in the mind of A.
Now call some of the variable accessible to A. Intuitively, this means that A has the possibility to measure the variable as accurately as he wishes. Mathematically, I only require
Postulate 2: If theta is accessible to A, and lambda is some fixed function of theta, then lambda is accessible.
Now I come to my main model assumption:
Postulate 3: In the given context there exists an inaccessible variable phi such that all the accessible ones are functions of phi.
As an example, we can let phi be the unit spin vector of some particle, say the qubit situation with spin 1/2, and define the accessible spin component in direction a as sign(cos(phi,a)), taking the values -1 and +1.
To go further, we need some definitions.
Definition 1. The accessible variable theta is called maximal if the following holds: If theta is a function of another variable psi, and this function is not bijective, then psi is not accessible.
In other words, theta is maximal under the partial order defined by taking functions.
Postulate 4: There exist maximal accessible variables.
The situation sketched here has been discussed from various points of views in the book [1], where the variables are called e-variables. A breakthrough came with the article [2], where the variables are called conceptual variables because they somehow exisr in the mind of A. An important correction to [2] was accepted today. I work now with summing up the whole theory in a new article [3]. The results turn out to be very simple in the case where theta takes a finite number of values. The following theorem will be demonstrated in [3]:
Theorem 1. Assume postulates 1 to 4, and that there exist two different maximal accessible variables theta and eta, each taking n values. Then there exists a Hilbert space H describing the situation, and every accessible variable will have a self-adjoint operator in H associated with it.
This is the starting point for developing QM from a new angle. Further results will be developed in [3], partly building upon previous published papers:
- The eigenvalues of the operator associated with theta are the possible values of theta.
- The variable theta is maximal if and only if all eigenvalues are non-degenerate.
- The two variables theta and eta are related: there exists a function f on phi-space and a transformation k in phi-space such that theta=f(phi) anf eta=f(k phi).
From this basis, the whole foundation of QM in the finite-dimensional case can be built up. A theory of continuous variables can in principle be developed by taking limits from the finite case.
The implications for the Bell experiment are discussed in [4]. An important observation is thet the physical variables in this theory can be replaced by decision variables. This gives a new foundation of quantum decision theory [5]. Unfortumately, Foundations of Physics would not print my important correction.
Another important observation is the following: The observator A can be replaced by a group of communicating observers, and the theory is still valid.
But the observer A can in principle be any human being. In a given (physical) situation, this largely detemines what we have in our minds, the basis for our actions, in particular for our written and spoken words. Our mental model. I have a model of this kind in my mind when I write this. In paricular, according to [4], my mind is limited, and I have to convince other people that this all makes sense.
In a similar way, I look at mental models as something which in a given situation lies behind everybody's action. In this sense, I personnally regard Alexey's model as too simple: In a series of long contribuions he tries to convince us about what he calls cencorship of believers in QM, and he uses word as 'unthikable fantasies'. In my view, these contrubutions may have prevented some of us to enter more interesting discussions.
What are my views on the interpretation of quantum mechanics? I support a general epistemic interpretation, where QBism is a special case. But there is also a relation to ontology [6]. In particular, Rovelli's interpretation seems to go together with mine. I also rely heavily on Hervé Zwirn's Convivial Solipsism: Every description of the world must be relative the mind of some observer. But people can communicate. The single observer A can be replaced by a group of communicating observers.
References:
[1] Helland, I.S. (2021). Episemic Processes. A Basis for Statistics and Quantum Theory. 2. edition. Springer
[2] Helland, I.S. (2022). On reconstructing parts of quantum theory from two related maximal conceptual variable. International Journal of Theoretical Physics 61, 69. Correction to appear.
[3] Helland, I.S. (2023). An alternative derivation of quantum states and operators. In preparation.
[4] Helland, I.S. (2022). The Bell experiment and the limitation of actors. Foundation of Physics 52,55.
[5] Helland, I.S. (2023). A simple quantum model linked to decisions. Foundation of Physics 53,12.
[6] Helland, I.S. (2021). Epistemological and ontological aspects of quantum theory. arXiv: 2112.10484 [quant-ph].
Sent: 01 March 2023 19:00
To: Алексей Никулов
Cc: Richard Gill; Austin Fearnley; Bell inequalities and quantum foundations; Inge Svein Helland
Алексей Никулов
You are wrongly attributing your delusion to others. The attitude to
quantum mechanics is unique in that almost everyone has their own
delusion. There are at least as many different delusions as there are
interpretations of quantum mechanics. More than ten different
interpretations are known and recognized, see “Interpretations of
quantum mechanics” at Wikipedia
https://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics .
There are obviously many more unknown and unrecognized
interpretations.
Your delusion is known as ‘instrumentalism’. So I advise you to read
Chapter 1 “The Theory of Everything” of the book [1] in which David
Deutsch (The Father of Quantum Computing, see
https://www.wired.com/2007/02/the-father-of-quantum-computing/?currentPage=all
) criticized instrumentalism. I advise you also to read the book [2]
of the famous philosopher of the twentieth century Karl Raimund Popper
who was understanding that the creators of quantum mechanics followed
the instrumentalist view. He also understood that “Very few physicists
who now recognize the instrumentalist point of view of Cardinal
Bellarmino and Bishop Berkeley realize that they accept some
philosophical theory. They also do not realize that they are breaking
with the Galilean tradition” [2].
Deutsch invented the idea of the quantum computer in the 1970s as a
way to experimentally test the "Many Universes Theory" of quantum
physics - the idea that when a particle changes, it changes into all
possible forms, across multiple universes. He understood that the
instrumentalist point was misleading about the reality of a quantum
computer in the one universe we know. Deutsch stated that “For even in
purely practical applications, the explanatory power of a theory is
paramount and its predictive power only supplementary” [1]. He argued
that a real device, for example an interstellar spaceship, can be made
on a theory explaining experimental results rather than a theory which
only predicts the outcomes of experiments.
I have proved mathematically in my manuscript “Quantum register cannot
be real” that a quantum computer cannot be real because of the obvious
mathematical fact that the operators of finite rotations of the
coordinate system can be applied only to non-entangled spin states.
The Editors of seven journals that rejected this manuscript did not
even try to refute this mathematical fact. The manuscript was rejected
without any justification in six journals and only in one journal on
the basis of comments of a Reviewer.
This Reviewer also did not refute the mathematical fact that the
operators of finite rotations of the coordinate system cannot be
applied to entangled spin states. He recommended not to publish my
manuscript on the basis of his worldview. This Reviewer, like you,
follows the instrumentalist view according to which a physical theory
should only predict but not explain experimental results. He even
stated that “The majority of physicists working in quantum mechanics
are instrumentalists”. I do not think that his statement is correct. I
know that most people believe in the reality of a quantum computer not
because they are instrumentalists but because they are naive realists.
Most people believe in the reality of a quantum computer because the
majority believe in it.
[1] D. Deutsch, The Fabric of Reality. The Penguin Press, 1997.
[2] Karl Raimund Popper, Conjectures and Refutations: The Growth of
Scientific Knowledge. Routledge and Kegan Paul, 1963.
With best wishes,
Alexey
ср, 1 мар. 2023 г. в 21:00, Mark Hadley <sunshine...@googlemail.com>:
Richard Gill
You wrote “ I have proved mathematically in my manuscript “Quantum register cannot
mathematical fact that the operators of finite rotations of the
coordinate system can be applied only to non-entangled spin states.
The Editors of seven journals that rejected this manuscript did not
even try to refute this mathematical fact. The manuscript was rejected
without any justification in six journals and only in one journal on
What you call an “obvious mathematical fact” is so obviously wrong that I understand the decisions of the editors of seven journals. If you send me a fresh copy of your paper it would be my pleasure to write a careful referee report for you. I have long suspected that you have become confused by the careless notation of many physicists working in this area. I well recall that it was a great barrier to myself, 25 years ago or more, when I first got addicted to debates on quantum foundations.
Yours
Sent from my iPad
>
> Dear Mark,
Mark Hadley
Алексей Никулов
Thank you for your interest in my manuscript. I am happy to send it to
you and anyone else who might be interested.
I think that the idea of a quantum computer became popular because
most physicists did not take into account that quantum computing
theory was created for a multidimensional Hilbert space, while qubits
and quantum registers must exist in the real three-dimensional space.
This remark cannot apply only to David Deutsch, who sincerely believes
in a multiverse that can be a material embodiment of the
multidimensional Hilbert space. But I cannot believe in the existence
of multiple universes, each with its own Deutsch.
The impossibility of a quantum computer in real three-dimensional
space can be proved as follows. Particles with spin 1/2 are typical
qubits. A system of N such qubits is a typical quantum register when
the qubits are entangled. The result of the calculation should be
obtained after a change in time of the quantum register in accordance
with the Schroedinger equation. The result of the calculation can only
be the probabilities of observing spin-up (or spin-down) of each of
the qubits. It is well known that these probabilities depend on a
direction in which spin projections of each particle are measured when
the particles are not entangled. Each non-entangled spin state has a
direction in the real three-dimensional space in which this spin state
is an eigenstate.
The probabilities in any other direction are determined unambiguously
with the help of the operators of finite rotations of the coordinate
system when qubits are not entangled. For example, if the eigenstate
is along the z-axis then measurement along the z-axis will give
spin-up with probability 1 and with probability 0.5 along the x-axis.
In this case of non-entangled qubits unambiguous probabilities exist
which we can consider as results of calculation by a quantum computer.
Although these probabilities depend on the direction in which spin
projections are measured.
But a quantum computer has an advantage only when the qubits are
entangled. The probability in this case cannot be determined
unambiguously since the operators of finite rotations of the
|Non-ent> = |A+z>|B-z> =0.5^{0.5}(|A+x> + |A-x>)0.5^{0.5} (|B+x> +
|B-x>) (1)
with the eigenstate along the z axis of the real three-dimensional
space, but cannot applied to the EPR state
|EPR> = 0.5^{0.5}(|A+,B-> + |A-,B+>) (2)
I draw your attention that the probability amplitude 0.5^{0.5} in (2),
in contrast to (1) cannot depend on the direction z or x in which spin
projection of the first particle is measured since we cannot know
which particle A or B will be measured first.
The probabilities of observing entangled qubits cannot be determined
unambiguously for any direction of measurement of spin projections
since the operators of finite rotations of the coordinate system
cannot be applied to entangled spin states. Then, what is the result
of quantum computer calculations?
With best wishes,
Alexey
чт, 2 мар. 2023 г. в 17:17, Richard Gill <gill...@gmail.com>:
Richard Gill
I have studied the abstract of your paper. It seems to me that it exhibits a number of gross mathematical misunderstandings (see below). I will now start reading the paper itself.
Richard.
AN: A quantum computer cannot be real since a quantum register must exist in the real three-dimensional space rather than in a multidimensional Hilbert space. Quantum states, according to Born’s proposal, describe the knowledge of the observer about the probability of results of upcoming observations. The knowledge of the observer about N qubits is described with the help of N-dimensional Hilbert space.
RDG: N qubits are described with a 2^N (complex) dimensional complex Hilbert space. In QM we must distinguish real physical space and various mathematically defined spaces. The motion of a real point particle in one-dimensional real space for instance, is conventionally described in QM with the help of the Hilbert space of equivalence classes of square integrable complex functions of one real variable, under the equivalence relation “norm if difference equals zero”.
AN: But any real device, including a quantum register, should exist in the real three-dimensional space. Spinors describe not only the probability to observe a spin projection, spin-up or spin-down, but also real spin states existing in the real three-dimensional space. The components of the spinor, like the components of a vector, undergo a linear transformation with a rotation of the coordinate system in the real isotropic three-dimensional space.
RDG: You are talking about a particular use of the mathematical objects called spinors. Spinors may also be used to describe other physical systems. The real 3D coordinate system used to specify transformations of “real” spin states may also be applicable to describe other three-real-parameter transformations of other systems. You are mixing up the use of the word “real” to denote real numbers (which are an invention of human imagination), and its use in talking about physically real 3D space.
AN: But the quantum register cannot describe real states in the real three-dimensional space since the operators of finite rotations of the coordinate system cannot be applied to spin states of entangled particles.
RDG: This is a non-sequitur, as I have explained.
AN: The entangled states can describe only the knowledge of the observer in agreement with the only correct definition of the EPR correlation as ’entanglement of our knowledge’ given by Schrodinger in 1935.
RDG: entangled states certainly describe the knowledge of an observer, if we agree with conventional QM. If the predictions of QM are generally correct, then they correctly describe the knowledge of an observer about reality. Those predictions do seem in practice to be extremely reliable.
AN: Therefore no quantum register can be real.
RDG: You repeat your earlier non sequitur.
Sent from my iPad
Richard Gill
I am reading your paper and I see repetition of well known opinions, earlier misunderstandings, etc; no news, no new insights. On page 9 I see the major failing of your logic, which I already identified in the abstract. You say “If someone who believes in the reality of the quantum register would claim that the spin states of the quantum register exist in reality, he will have to answer the question to which coordinate system of the real three-dimensional space the amplitudes … in the expression (8) refer.”
No. Why should the three real dimensions of the quantum description of a qubit (any two level quantum system) necessarily have to correspond to the three real dimensions of real 3D space in the laboratory?
You need to study the textbook of Nielsen and Chuang, or another introductory text on quantum information theory. You need to become familiar with the mathematical notion of isomorphism. The correspondence between the mathematical spaces which physicists helped discover (which they needed in order to describe nature) and the physical space in which their experiments and observations take place, can be incredibly indirect.
Yours
Richard
Sent from my iPad
Richard Gill
Later in your paper you get to Popper. Karl Popper was sometimes mistaken. You wrote
“Speaking about breaking with the Galilean tradition, Popper meant that according to the instrumentalist point of view no difference was between the Ptolemaic system and the Copernican system in the time of Galileo, since both systems successfully described the results of observations known in that time. The reason for the conflict with the Catholic Church was Galileo’s assertion that the Copernican system is not just a more convenient instrument for describing the results of observations, but is a description of reality. The Galilean tradition led to space flights, which would hardly have been possible if the instrumentalist point of view had won.”
Both systems were not equally succesful. The Copernicus system was more parsimonious. Less “free parameters”. The Copernican system was more beautiful. More “natural”. However, it was only a partial success in that direction. Kepler killed the Ptolemaic system by switching from circles to ellipses. Copernicus was still infected by the ideology that creation was the work of God, and He would only use ideal geometric objects in His creation. Newton gave the final blow to the Ptolemaic system by explaining both terrestrial and cosmic motions with one simple (though stunning, because non-local) law depending on mass, location and velocities. Of course, ordinary folk, especially sailers, already knew the earth was a globe; the telescope showed that the planets were globes and had moons. So it was all not so simple as Popper suggested.
Imre Lakatos (“Conjectures and refutations”) is a great antidote to Popper. (Popper was great, but he too was human and a child of his time).
Richard
Sent from my iPad
Алексей Никулов
RDG: entangled states certainly describe the knowledge of an observer,
if we agree with conventional QM.
whereas quantum computation must be performed outside of the mind of
the observer, i.e. in reality. The idea of a quantum computer is based
on the main absurdity of quantum mechanics, which E.T. Jaynes wrote
about more than forty years ago, but which most do not want to
understand up to now:
“From this, it is pretty clear why present quantum theory not only
does not use—it does not even dare to mention—the notion of a "real
physical situation." Defenders of the theory say that this notion is
philosophically naive, a throwback to outmoded ways of thinking, and
that recognition of this constitutes deep new wisdom about the nature
of human knowledge. I say that it constitutes a violent
irrationality, that somewhere in this theory the distinction between
reality and our knowledge of reality has become lost, and the result
has more the character of medieval necromancy than science” [1].
[1] E.T. Jaynes, "Quantum beats," in Foundations of Radiation Theory
and Quantum Electrodynamics, A.O. Barut (ed.) (New York: Plenum Press,
1980).
With best wishes,
Alexey
чт, 2 мар. 2023 г. в 19:35, Richard Gill <gill...@gmail.com>:
Mark Hadley
Алексей Никулов
AN: If someone who believes in the reality of the quantum register
reality, he will have to answer the question to which coordinate
system of the real three-dimensional space the amplitudes … in the
expression (8) refer.
to correspond to the three real dimensions of real 3D space in the
laboratory?
know the results of the quantum computation? According to the general
belief, the probability to observe ‘spin up’ or ‘spin down’ of
particles with spin 1/2 of quantum register should be measured. Spin
projection should be measured in a direction of the real space. I
repeat that the measurement result depends on the direction in which
the spin projections are measured. Therefore, the result of the
calculation depends on the direction in which the projections are
measured. We chose one direction and got the result of calculations,
we chose another direction and got a different result of calculations.
What is the meaning of such calculations?
Nielsen and Chuang are profane people who do not understand the
physics of what they are writing about.
With best wishes,
Alexey
чт, 2 мар. 2023 г. в 20:17, Алексей Никулов <nikulo...@gmail.com>:
Richard Gill
 | |
Richard Gill
 | |
 | |
Richard
Алексей Никулов
Dear Richard, You understand too quickly. And that means you don't understand what I'm trying to explain to you. In fact, you do not understand, but compare it with what you are used to and what you believe in. Because of this you do not understand even the obvious fact that the idea of a quantum computer is false because the results of its calculations cannot exist. I will try to explain this fact to you as clearly and popularly as possible, and you try to understand it before making conclusions.
I hope you know that the result of the calculation of a quantum computer should be the probabilities P of observation, for example, the projection of spin on the chosen direction, for example the z axis. To find the probability P = n_{up}/n for each qubit, we must perform the same quantum calculation many times ‘n’ and determine how many times n_{up} the result ‘spin-up’ was observed during ‘n’ measurements. In order for probability P_{z} = n_{up}/n to make sense, measurements must be carried out in the same direction z and in the same spin state. The spin states are the same when they have their eigenstates in the same direction, for example z1. It is also necessary that the probability P_{z} = n_{up}/n in the direction z is uniquely determined in the spin state having eigenstates along z1. This uniqueness is provided by the operators of finite rotations of the coordinate system. In order for a given qubit to be in the same state with eigenstate along z1 after each of ‘n’ quantum calculations, this state and this eigenvalue must exist.
These requirements for the possibility of the existence of quantum computing results are met for spin states, but only when they are not entangled. I hope you know that states are not entangled when the expression for N qubits can be decomposed into factors describing each qubit.
It is obvious that the particles A or B in the EPR state
|EPR> = 0.5^{0.5}(|A+,B-> + |A-,B+>) (1)
cannot have eigenstates and the operators of finite rotations of the coordinate system cannot be applied to these particles since the first measurement of any particle in any direction will give ‘spin-up’ (+) with probability P1 = 0.5 according to (1). I draw your attention that the probability amplitude 0.5^{0.5} in (1) cannot depend on the direction in which spin projection of the first particle is measured since we cannot know which particle A or B will be measured first.
According to your belief in the EPR correlation the measurement of the second particle along the same direction z should give the opposite result with probability 1. Thus, the measurement of the first particle along z should give ‘spin up’ (+) or ‘spin down’ (-) with probability 0.5 and the measurement of the second particle along z should give ‘spin down’ (-) or ‘spin up’ (+) with probability 1. What can be the results of quantum computing here? The EPR state (1) describes at least the knowledge of the observer about results of measurements of the first and second particles. The entangled spin states with the number of qubits greater than two do not describe even the knowledge of the observer.
With best wishes,
Alexey
Richard Gill
On 3 Mar 2023, at 11:02, Алексей Никулов <nikulo...@gmail.com> wrote:
Dear Richard,You understand too quickly. And that means you don't understand what I'm trying to explain to you. In fact, you do not understand, but compare it with what you are used to and what you believe in. Because of this you do not understand even the obvious fact that the idea of a quantum computer is false because the results of its calculations cannot exist. I will try to explain this fact to you as clearly and popularly as possible, and you try to understand it before making conclusions.
I hope you know that the result of the calculation of a quantum computer should be the probabilities P of observation, for example, the projection of spin on the chosen direction, for example the z axis. To find the probability P = n_{up}/n for each qubit, we must perform the same quantum calculation many times ‘n’ and determine how many times n_{up} the result ‘spin-up’ was observed during ‘n’ measurements. In order for probability P_{z} = n_{up}/n to make sense, measurements must be carried out in the same direction z and in the same spin state. The spin states are the same when they have their eigenstates in the same direction, for example z1. It is also necessary that the probability P_{z} = n_{up}/n in the direction z is uniquely determined in the spin state having eigenstates along z1. This uniqueness is provided by the operators of finite rotations of the coordinate system. In order for a given qubit to be in the same state with eigenstate along z1 after each of ‘n’ quantum calculations, this state and this eigenvalue must exist.
These requirements for the possibility of the existence of quantum computing results are met for spin states, but only when they are not entangled. I hope you know that states are not entangled when the expression for N qubits can be decomposed into factors describing each qubit.
It is obvious that the particles A or B in the EPR state
|EPR> = 0.5^{0.5}(|A+,B-> + |A-,B+>) (1)cannot have eigenstates and the operators of finite rotations of the coordinate system cannot be applied to these particles since the first measurement of any particle in any direction will give ‘spin-up’ (+) with probability P1 = 0.5 according to (1). I draw your attention that the probability amplitude 0.5^{0.5} in (1) cannot depend on the direction in which spin projection of the first particle is measured since we cannot know which particle A or B will be measured first.
According to your belief in the EPR correlation the measurement of the second particle along the same direction z should give the opposite result with probability 1. Thus, the measurement of the first particle along z should give ‘spin up’ (+) or ‘spin down’ (-) with probability 0.5 and the measurement of the second particle along z should give ‘spin down’ (-) or ‘spin up’ (+) with probability 1. What can be the results of quantum computing here? The EPR state (1) describes at least the knowledge of the observer about results of measurements of the first and second particles. The entangled spin states with the number of qubits greater than two do not describe even the knowledge of the observer.
With best wishes,
Alexey
чт, 2 мар. 2023 г. в 21:20, Richard Gill <gill...@gmail.com>:
Alexei, you do not understand Nielsen and Chuang’s mathematics. Your question is adequately answered in their book.About Jaynes: in the very old paper by him which you cite he is struggling with the measurement problem,
I consider that the measurement problem is adequately solved from a mathematical point of view through a well-chosen Heisenberg cut, according to the principle developed by Slava Belavkin, his so-called non-demolition principle, see my expository paper on “eventum mechanics”.
<preview.png>
Алексей Никулов
Dear Richard, You are in a hurry to understand again and do not want to think. That's why you didn't understand anything again. I have no doubt that
a number of qubits are measured simultaneously, many times. I tried to explain to you not how measurements are made, but that the
result of quantum computing cannot exist. Try to understand this and not draw conclusions without understanding.
You agree that “Entangled states of 2 or more qubits *do* describe the knowledge of an observer”. Now try to understand that it
logically follows that quantum computing is impossible without the observer's mind if entangled states describe only the knowledge of
an observer. I tried to explain to you that non-entangled spin states describe not only the observer's knowledge, but also real spin states
that can change in time between observations regardless of the observer's mind. This change in time of real spin states is the process of
quantum computing, which is possible if qubits describe not only the knowledge of the observer, but also real states that exist
independently of the observer's mind.
I have read Nielsen and Chuang. I got the impression that Nielsen and Chuang are mathematicians who have extremely naive notions
about quantum mechanics. Extreme naivety is their confidence that the Stern-Gerlach experiment gives evidence of the real existence of
qubits in Nature. To understand that this is foolishness, you need to know, as Bell knew, that it was experiments such as the
Stern-Gerlach experiment that forced the creators of quantum mechanics to abandon the description of Nature: ”Phenomena of this kind m
made physicists despair of finding any consistent space-time picture of what goes on the atomic and subatomic scale” [1].
[1] J.S. Bell, Bertlmann’s socks and the nature of reality. Journal de Physique, 42, 41-61 (1981).
With best wishes,
Alexey
Richard Gill
Алексей Никулов
Dear Richard, Your unflattering opinion of Ed Jaynes cannot refute the rightness of his understanding that quantum mechanics entangled reality with
our knowledge of reality. You yourself confirm this absurdity of quantum mechanics by now admitting, now denying that
“Entangled states of 2 or more qubits *do* describe the knowledge of an observer”. Your thinking is not clear and definite, as is the
thinking of most scientists who believe but do not understand quantum mechanics. This blind faith has led to monstrous consequences:
most scientists simply do not know how to think logically because of this belief.
7 journals did not accept my paper because science has become mass, and mass-man does not know how to think critically and
blindly believes in what the majority believes.
With best wishes,
Alexey
GeraldoAlexandreBarbosa
Alexey,
Please forgive me to say that your concept of reality may obscure your understanding of quantum mechanics.
Just to lead you to a strange land that (I imagine) does not fit into your vision of QM, think about a single photon state with several degrees of liberty. I should assume that spin (helicity) and polarization are acceptable to you. I believe I can add linear momentum as well. Let me also add orbital angular momentum L; each photon may carry values l=-{L …0 …L}.
There are quantum computation operations that act on these variables (we may call these operations “gates”). Due to the (assumed) entanglement between variable components, we may say that they are represented by “qubits”. [In case you don’t accept the notion of entanglement, this leads to a different discussion).
In a quantum computation operation (say, an optical quantum computer), the input is represented by qubits. For example, polarization can be a qubit, orbital momentum another qubit, and even space position (momentum) another qubit.
Each gate operation can act on the input qubits to produce a new state to be acted by the following gate. The final result, or output of quantum calculation, may be detector clicks (classical signals) representing the desired calculation.
In other words, the “calculation” is given by the evolution of states according to the gate “rules”. Different variables may influence each other on a complex way.
The gates act on the wave function “space”, Not just on the 3D space. The quantum “computer” circuitry is set on the 3D space, but the processing act on a multitude of variables. If one’s mind does not accept the wave function picture, written in a Hilbert space, where the operators act, things became very confused.
[If the notion of entanglement is not accepted, nothing said above makes sense, of course]
Geraldo
Richard Gill
Austin Fearnley
I read your two recent posts with interest. My physics work since c 2010 has focused on preons and Bell. My work on Bell has been to make simple computer simulations. A difficulty in working on local hidden variable models is that they cannot defeat Bell('s Theorem). I eventually (2019?) attacked Malus('s Law) which held out hope of finding a particle model to give Malus outcomes as it is not a no-go Theorem. I very quickly (c2020) had a classical. gyroscopic model of an elementary particle which conformed with Malus outcomes. And, if retrocausality was added (c2022), the method defeated Bell by bypassing it because what was going on in a (very simple) Bell experiment was different to the usual interpretation because of the retrocausality.
So my views have kept changing. In 2022 I held the view that my model had no place for a quantum computer (simply because there was no entanglement in my model) but as a very narrow-focus amateur, my reading around this physics topic was limited. Richard kindly pointed me in 2022 at several of his quantum computing papers and my view softened a little. So I now accept that quantum cryptography is possible within my retrocausal model. (Moreover I suspect that sending messages through time using retrocausality may be more possible than is generally accepted without retrocausality.) I am still rather skeptical about quantum computers. I did follow, in Richard's papers, the sort of calculations based on entangled particles as they pass through gates. If this is merely information then of course I accept those calculations. But I do not accept that the particles themselves do not have individual polarised states at all times. So my view changed to accepting that if the quantum computer using composite or statistically aggregated states rather than ontic states can give results, then that is OK. I could accept that quantum computers work by computing statistics in the minds of the computer operators. Well, NO, not that! But, yes, by the proxy of the quantum algorithms standing in for the minds of the observers.
After your first recent post I was inspired to read about 'down conversion' and was interested about increased coherence leading to more densely pack information through optical cables. All new to me.
In your recent post, doesn't a gate change (at that very gate) the polarisations of the particles passing through? Those are measurements. Can the effects of these changes in polarisations be deferred until the final quantum computer calculation. Well, I think I can accept that the outcomes can be held as composite states until the calculation at the end of the process. You have gate logic to predict the post-gate states. I have a computer program and particle model to predict the outcomes of Stern Gerlach measurement which is a similar affair.
My bypassing of Bell's Theorem using retrocausality allows me to replace QM ontic mixed states by simple statistical composites of separate states. Bell's Theorem cannot prevent this occurring in my retrocauseal model. I have here talked myself into being more believing in quantum computers an previously - though without using QM ontic entangled mixed states.
Austin
Алексей Никулов
Dear Geraldo,
You do not take into account that in addition to your understanding of quantum mechanics, there are many other understandings that are
different from yours and even contradict it. Only known and recognized interpretations of quantum mechanics exist more than ten.
Unknown and unrecognized interpretations are many more. This chaos in understanding is a direct consequence of the adaptation of the
concept of reality to the possibility of describing paradoxical quantum phenomena by the creators of quantum mechanics. This chaos
proves once again the correctness of what ’cultured’ men about 1750 understood: our concept of reality should not depend on any
theories or phenomena. As Kant has understood, realism and determinism are regulative principles of our reason, which determines the
very possibility of empirical cognition of Nature.
Einstein, like Kant, understood that realism is ”the presupposition of every kind of physical thinking” rather than a claim which can be
disproved with any experimental results. According to Einstein’s understanding, the rejection of realism means the rejection of
physical thinking. The substitution of various and contradictory fantasies for physical thinking indicates that Kant and Einstein were
right.
You want to lead me to a strange land that (you imagine) does not fit into my vision of QM, and propose me to think about a single
photon state with several degrees of liberty. I must remind you once again that the concept of light quanta, which began to be called
photons, was introduced by Einstein in 1905. Anyone who thinks he understands what light quanta is should know what Einstein said to
his friend Michele Besso in 1951:“All these fifty years of conscious brooding have brought me no nearer to the answer to the question,
‘What are light quanta?’ Nowadays every Tom, Dick and Harry thinks he knows it, but he is mistaken”. The concept of light quanta is
so absurd that almost no one, not even Bohr, admitted it before the advent of quantum mechanics. Bohr and every Tom, Dick, Harry
have admitted this concept due to Born’s proposal to describe the knowledge of the observer about probability of results of upcoming
observation. But the author of this concept, Einstein, did not agree with such a solution to the problem of quantum dualism, which he
himself provoked, at the cost of abandoning realism.
To justify the rejection of realism Heisenberg has been calling the ‘old-fashioned’ attitude toward the problem of reality as dogmatic
realism and metaphysical realism: ”Dogmatic realism claims that there are no statements concerning the material world that cannot be
objectivated · · · actually the position of classical physics is that of dogmatic realism. It is only through quantum theory that we have
learned that exact science is possible without the basis of dogmatic realism. When Einstein has criticised quantum theory he has done
so from the basis of dogmatic realism” [1]. Einstein’s famous dictum ”I like to think that the moon is there even if I don’t look at it” is
a manifestation of dogmatic realism.
Dogmatic realism is not an extreme form of delusion according to Heisenberg: ”Metaphysical realism goes one step further than
dogmatic realism by saying that ’the things really exist’. This is in fact what Descartes tried to prove by the argument that ’God cannot
have deceived us’” [1]. Einstein would have said, ”I’m sure that the moon really exists even if I don’t look at it,” if he had followed
metaphysical realism. Einstein followed dogmatic rather than metaphysical realism since he was understanding the validity of Kant’s
avowal that ”it always remains a scandal of philosophy and universal human reason that the existence of things outside us (from which
we after all get the whole matter for our cognitions, even for our inner sense) should have to be assumed merely on faith, and that if it
occurs to anyone to doubt it, we should be unable to answer him with a satisfactory proof” [2].
The rejection of realism by the creators of quantum mechanics has led to a mass delusion, primarily because almost all scientists are
naive realists who cannot doubt that ’the things really exist’. You don't doubt even that polarization really exists, whereas creators of
quantum mechanics because of such quantum phenomena as the Stern-Gerlach effect “asserted that atomic and subatomic particles do
not have any definite properties in advance of observation. There is nothing, that is to say, in the particles approaching the magnet, to
distinguish those subsequently deflected up from those subsequently deflected down. Indeed even the particles are not really there” [3].
The illusion of the reality of a quantum computer became possible precisely because most scientists, being naive realists, did not
understand what the rejection of realism by the creators of quantum mechanics means. When you write “Each gate operation can act
on the input qubits to produce a new state to be acted by the following gate” you are sure a state can really exist. But this confidence of
yours contradicts quantum mechanics, at least in the case of the entanglement of our knowledge. The impossibility of the real existence
of entangled spin states follows from the mathematical fact that the operators of finite rotations of the coordinate system are applicable
only to non-entangled spin states.
The authors of the GHZ theorem [4] made an obvious mistake by not taking into account this obvious mathematical fact. The mistake was
so obvious that I was surprised that it could have been made when I noticed it. According to the expression for the GHSZ state (7) in [4]
‘spin up’ should be observed with the probability 1/2 in any direction of the real three-dimensional space, while according to the
Appendix F of all four particles of the GHSZ state have eigenstates along the same direction, measurement spin projections along which
should give ‘spin up’ with probability 1. This obvious mistake became possible since the authors of the GHZ theorem [4] did not
take into account that entangled spin states cannot have eigenstates since the operators of finite rotations of the coordinate system are
applicable only to non-entangled spin states. The expression (8) for the expectation value, on the base of which the GHZ theorem was
derived in [4], does not make sense, since the angles between the direction in which the spin projection is measured and the direction of
the eigenstate does not make sense if there cannot be an eigenstate. Thus, the authors [4] refuting realism made obvious mistakes since
even they are naive realists.
[1] W. Heisenberg, Physics and Philosophy, George Allen and Unwin Edition (1959).
[2] I. Kant, The Critique of Pure Reason, Cambridge Univ. Press (1998).[3] J.S. Bell, Bertlmann’s socks and the nature of reality. J. de Physique 42, 41 (1981).
[4] D.M. Greenberger, M.A. Home, A. Shimony and A. Zeilinger, Bell’s theorem without inequalities, Amer. J. Phys. 58, 1131 (1990). With best wishes,
Alexey
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/0866f7c4-7433-41f8-89be-f59f465dd560n%40googlegroups.com.
GeraldoAlexandreBarbosa
Alexey,
Trying to make short a discussion about realism, in my view, if sensors (human or equipment) are able to show consistent measurements with repeated outcomes, the thing being measured can be assigned as “real”. As I said before, this concept of real or reality it is just a model in your mind, an odd flashing of neurons that gives you the sensation of consciousness – and that you, Alexey, have no clear idea of what it means.
Geraldo
Алексей Никулов
Realism has nothing to do with sensors. Try to understand what
Einstein understood: realism is ”the presupposition of every kind of
physical thinking”. It is easy to understand without philosophy why
realism determines the very possibility of empirical cognition.
Realism (dogmatic according to Heisenberg) states that the moon exists
even if no one looks at it. Therefore, we must explain how our mind
creates the moon when observing if we reject realism.
I have to say that your thinking is contradictory. On the one hand,
you write that “Each gate operation can act on the input qubits to
produce a new state to be acted by the following gate” and on the
other hand we claim that “the thing being measured can be assigned as
“real””. Each gate operation must be between measurements and
therefore it cannot be real according to your definition. Or do you
think that the process of quantum computing may be unreal?
With best wishes,
Alexey
пн, 6 мар. 2023 г. в 17:33, GeraldoAlexandreBarbosa <geraldo...@gmail.com>:
Richard Gill
In physics, one tries to explain empirical observations (and to predict empirical observations) through mathematical theories. In those theories all kinds of “things” are talked about - particles, waves, fields …. Philosophers then argue about whether some of those items can be given a special status and be called “real”. Different interpretations of quantum theory assign more or less “reality” to different parts of the mathematical structure. But they all agree with the computations and the computations tell us about real things - for instance, the probability distribution of outcomes of measurements.
Are you saying that the statistics of results of lab experiments are not real?
Only the Many World people say that they are not real, they say only the wave function is real.
QBists and the like talk about information, and some of them have a subjective interpretation of probability. Others have a frequentist interpretation. The results are the same.
Einstein’s statement is nice but completely useless since he does not say what is entitled to be called real, and what isn’t.
I think that it is a good working approach to physics to suppose that the moon is there even if nobody looks at it. It is obvious how our mind created the notion of “moon”, and it is obviously a very useful notion.
I think you are misunderstanding Geraldo. When he says “the thing being measured is real” I suppose he means that the measurement outcome is real. “The thing being measured” is the state of a quantum system which is an object in a mathematical theory. The measurement outcome is “up” or “down” (or a sequence of such binary outcomes). It can be duplicated, printed out, saved on a hard disk of a computer and retrieved again later.
Alexei, I think your thinking is contradictory and moreover it seems to be stuck at the phase in which quantum mechanics was, 80 years ago. A lot happened since then. Both on the philosophy side, and on the mathematical side, and on the engineering side.
Richard Gill
Sent from my iPhone
GeraldoAlexandreBarbosa
Alexey,
“Realism has nothing to do with sensors”.
It seems that the idea of sensors -in the most general sense- is not important to you. On the other hand, for me, sensors define even what you call reality (and your dreams).
The recording of sensors is what defines the classical logs (or the “classical world”). Whenever outputs from a quantum processor are recorded, they became classical records (that can read over and over again). The quantum mechanics models are justified by these “classical” records. They match what is predicted by QM - and perhaps not by classical physics. QM and your real world are just models.
The wave state evolution (steps) within a quantum computer is not accessible to our sensors. However, the QM predictions about this evolution and the resulting final outcome justifies the model. It seems that your idea of reality does not fit QM.
“Realism (dogmatic according to Heisenberg) states that the moon exists
even if no one looks at it. Therefore, we must
explain how our mind
creates the moon when observing if we reject realism”.
“… we must explain …”
No need to! ... and, again: The recording of sensors is what defines the classical logs (or the “classical world”).
Geraldo
Richard Gill
Mark Hadley
--
You received this message because you are subscribed to the Google Groups "Bell inequalities and quantum foundations" group.
To unsubscribe from this group and stop receiving emails from it, send an email to Bell_quantum_found...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/C80D961F-C062-4560-9FD3-1E40D9D3C31F%40gmail.com.
Austin Fearnley
I struggle with 'reality' as I know it is illusory. Oddly enough, it was a fine arts graduate who in 1971 warned me off using the term 'real' and I still try to avoid it.
However, I am inclined to think that chirality is more real than helicity. This has to do with having a model cope with all observers, for example QED because Feynman integrated SR into QM. Even chirality depends on the space in which it is observed. Would chiral LH still be LH if viewed in a very different space (eg dS versus AdS)?
I have been bending towards accepting that quantum computers can work even though I deny the 'reality' of entangled state |ud> + |du> for particles 1&2 [ignoring weighting factor]. The reality IMO is more likely to be |u> for particle 1 and |d> for particle 2, or vice versa. BI cannot be used to deny this opinion if retrocausality is occurring. But whichever case is more true, one can still accept composite successions of states after more and more interactions in the quantum computer and agree with the final calculation. So does it matter what the reality of entanglement states is? What QM gains with action at a distance (or whatever is the interpretation) my retrocausal method gains with an apparently faster than light effect but using separated states.
Austin
Алексей Никулов
Einstein, who saturated himself with Kant philosophy, understood that
we can know in Nature only what we have put ourselves into it, i.e. we
can know only our ideas about Nature, but not Nature as
thing-in-itself. Since we create our ideas ourselves neither Einstein
nor anyone else can question “what is entitled to be called real, and
what isn’t” in our ideas. The answer to this question is determined by
our a priori knowledge rather than empirical knowledge. For example,
the statistics of results of lab experiments are real when, according
to our ideas, they do not depend on our mind. Quantum mechanics
contradicts realism, because of the impossibility to describe some
quantum phenomena, such as the Stern-Gerlach effect, as a
manifestation of reality existing independently of our consciousness.
I once again draw your attention to the fact that the creators of
quantum mechanics have not explained why discrete values of
projections of the magnetic moment of atoms are observed. Instead,
they created quantum mechanics predicting only the probability of
observing various discrete values of spin projections. The probability
of observing cannot be real if it should change because of
observation, since our knowledge changes at observation. Our knowledge
about the probability can be entangled.
For example, two observers Alice and Bob know that two balls, red and
blue, are in a closed box. Bob takes one ball without looking, and
drives away with it at an arbitrarily long distance. Alice, before she
looks at the remaining ball, knows that Bob will see the blue ball
with a probability of 0.5 and with the same probability of the red
ball. Her knowledge can be described using the expression for the EPR
pair
|EPR> = 0.5^{0.5}(|A+,B-> + |A-,B+>) (1)
Bob’s ball. The knowledge of Alice will change when she will see the
red ball, for example. The new knowledge may be described with the
help of the expression
|New> = |A+>|B-> (2)
which means that Alice will see the red ball with the probability of 1
during the second observation, and Bob will see a blue ball with the
same reliability.
I hope you understand that Alice’s knowledge about the probability is
not real since any knowledge belongs to our mind. But according to our
ideas, the color of the balls, red or blue, is real, because this
color exists regardless of whether we know or do not know what the
color of this ball is. I explained very clearly and even popularly in
the preprint “Logical proof of the absurdity of the EPR correlation“
that spin projections, unlike the color of the balls, cannot be real
since the projections can be measured in different directions and
therefore spin projection cannot exist before observation according
elementary logic which belongs to our a priori knowledge. For some
reason, you do not want or cannot understand this elementary logic. To
make this logic understandable even to schoolchildren, I marked the
spin projections in different directions with different colors in Fig.
1 of the preprint
https://www.researchgate.net/publication/331584709_Logical_proof_of_the_absurdity_of_the_EPR_correlation
available on ResearchGate
https://www.researchgate.net/profile/Alexey_Nikulov/research .
The spin projections cannot be real in our ideas because of the
paradoxality of the Stern-Gerlach effect: binary outcomes are observed
both in the case of balls, red or blue, and spin projections of
particles with spin 1/2, spin up or spin down, but spin projection can
be measured in different directions.
I am understanding Geraldo correctly. He, like most people, believes
in quantum mechanics and does not want to understand that quantum
mechanics is a trick rather than physical theory. He does not want to
understand that the thing being measured is real if this thing exists
before the measurement, more precisely observation.
I draw your attention to the fact that mathematics should describe the
probabilities of binary outcomes in the same way, regardless of
whether the color of the balls, the projections of the spins or the
Schrodinger cats are observed. I draw your attention that the same
expression for the EPR pair (1) can describe entanglement of our
knowledge both about two balls and spin projections of two particles.
The difference is that the color of the balls exists before
observation, while the projections of the spins cannot exist. Not only
a spin projection, but even spin states of particle A and B do not
exist before the first observation. The mind of the observer should
create the spin projection and spin state only of the observed
particle according to the orthodox quantum mechanics and of both
particles according to Bohm’s quantum mechanics. The observer having
free will can create different spin states simply measuring the spin
projection of one of the particles in different directions.
According to Bohm’s quantum mechanics Alice will create the spin states
|New_{z}> = |A_{z}+>|B_{z}-> (3)
with the help of the measurement of spin projection along the z axis
or the other spin states
|New_{x}> = |A_{x}+>|B_{x}-> (4)
with the help of the measurement of spin projection along the x axis.
I draw your attention that the expressions (3) for z direction, (4)
for x direction and such expressions for any direction provide the EPR
correlation and violation of Bell’s inequalities.
You are sure that the outcomes of a quantum computation are real. But
what can be the outcomes of a quantum computation? The EPR pair (1)
can be considered as a quantum register consisting of two qubits. What
can be the outcomes of a quantum computation in this case if the first
measurement of a particle in any direction will give ‘spin up’ or
‘spin down’ with the probability 0.5 and the measurement of the second
particle will give the opposite result with the probability 1
according to (3) and (4)?
You think my thinking is stuck at the phase in which quantum mechanics
was, 80 years ago. And you wrote that “A lot has happened since then”.
Indeed, a lot has happened since then. The physical thinking of almost
all scientists has degraded so much since then that it terrifies me.
This degradation occurred for two main reasons: 1) science has become
mass and 2) quantum mechanics 80 years ago was a trick which was
misleading in that time as it is now.
I read both Belavkin’s and your papers. I must say that Belavkin and
you do not understand quantum mechanics. No problem with measurement
is in quantum mechanics. Quantum mechanics uses a trick with
‘observation’ rather than with ‘measurement’. Try to understand why
Bell was saying in his famous 1989 report “Against Measurement”:
“Einstein said that it is theory which decides what is 'observable'. I
think he was right - 'observation' is a complicated and theory-laden
business. Then that notion should not appear in the formulation of
fundamental theory”. The notion of ‘observation’ or ‘measurement’
should not appear in the formulation of a fundamental theory, as this
is a trick that has misled several generations of physicists. Instead
of resolving the measurement problem or offering different
interpretations in order to justify the obvious trick, it is necessary
to at least try to describe, for example, the Stern-Gerlach effect
without this trick.
With best wishes,
Alexey
ср, 8 мар. 2023 г. в 02:15, Austin Fearnley <ben...@hotmail.com>:
Richard Gill
I read Kant and Hegel as a teenager and there is much in Kant which I appreciate but I think that by now, Einstein’s understanding of Kant’s philosophy is getting pretty irrelevant. I am not a professonial philosopher and not a professional philosopher of science. I’m a professional mathematician. I would be interested to learn about current views by relevant professionals on these topics. I refer you to the recent beautiful work of Paul Raymond-Robichaud who has a beautiful and very careful analysis of the notions of realism and locality. People in this group should try to read his work and discuss it here!
I agree with you on one important matter. In my opinion, quantum mechanics does not *explain* the physical phenomena which it talks about. It only describes and predicts them very well. I do not agree that “Alice’s knowledge about the probability is not real since any knowledge belongs to our mind”. That knowledge is knowledge of real past experience. Moreover, it is past experience shared by all other “actors” we know about. Like some others here, I like the view called convivial solipsism.
In my opinion, the phenomena explored in Bell type experiments cannot be *explained*. I used to find that extremely disturbing. But having thought about this for 30 years, I don’t have a problem with that right now. I’m prepared to change my mind if new theories come up or new data. I don’t think that retrocausality or super determinism is an *explanation* (sorry, Ben). I don’t think that MWI explains anything. I think that decoherence theory only makes things more undecidable.
You dismiss the Belavkin approach too easily. You find an excuse in some words of John Bell not to study the mathematics or to work through the consequences for physics. Of course, all observation is theory-laden. Bell experiments and their interpretation depend on prior theoretical assumptions about measurement and determination of space and time, and assumptions about “when” measurement outcomes become “real”. There’s no escape from that. We must make clear what are the assumptions we are using when we try to make deductions from observation of reality.
I am still waiting for your solution to the problems raised by the actual results of the most careful Bell experiments. All you seem to have to say is that physics has taken a wrong turn because the young don’t know Kant any more. Sorry, but that is the kind of thing that old scientists have always said about present day science (going all the way back thousands of years!). What are you hoping is going to happen next? Suppose physicists start listening to you: what concrete steps should they take? What maths should they learn? What experiments should they try to do?
Yours
Richard
Алексей Никулов
Physics has taken a wrong turn not at all because the young don’t know
Kant any more. Heisenberg knew the philosophy not only of Kant and
Plato, but also of other philosophers. He wanted to study the
philosophy of science and wrote in his memoirs about his conversation
with Sommerfeld in 1920:
"Even so, I am much more interested in the underlying philosophical
ideas than in the rest," I said rather bashfully.
But Sommerfeld would have none of this. "You must remember what
Schiller said about Kant and his interpreters: 'When kings go
a-building, wagoners have more work.' At first, none of us are
anything but wagoners" [1].
Young Heisenberg decided to overthrow ‘king’ Kant because of the
illusion inherent in almost all modern scientists that Nature should
always be cognizable for our reason. In order to maintain this
illusion he proposed to describe not what exists, but what is
observed. He was able to mislead almost all scientists with this
trick, with the exception of Einstein and a few others. Einstein tried
to explain to Heisenberg back in 1926:
”But on principle, it is quite wrong to try founding a theory on
observable magnitudes alone. In reality the very opposite happens. It
is the theory which decides what we can observe. You must appreciate
that observation is a very complicated process. The phenomenon under
observation produces certain events in our measuring apparatus. As a
result, further processes take place in the apparatus, which
eventually and by complicated paths produce sense impressions and help
us to fix the effects in our consciousness. Along this whole path -
from the phenomenon to its fixation in our consciousness-we must be
able to tell how nature functions, must know the natural laws at least
in practical terms, before we can claim to have observed anything at
all” [1].
Don't you understand from this explanation that quantum mechanics from
the very beginning was a trick that hid the impossibility of
describing some quantum phenomena in the process of observation? This
trick had tremendous consequences due to the success of quantum
mechanics. The long-standing dispute about the EPR correlation and
Bell's inequalities, the idea of quantum computing and convivial
solipsism as the apotheosis of stupidity are all the result of the
funny trick.
In your opinion, the phenomena explored in Bell type experiments
cannot be *explained*. This opinion of yours is a great progress in
understanding. Now you must understand that orthodox quantum mechanics
does not predict the violation of Bell's inequalities and that these
inequalities could not have appeared if the creators of quantum
mechanics had not falsely replaced the trick with ‘observation’ with
a trick with ‘measurement’. You should understand that Bell's
inequalities have become popular because, according to our ideas, the
measurement process, unlike the observation process, is real. But the
trick with measurement is no better than the trick with observation.
[1] W. Heisenberg, PHYSICS AND BEYOND. ENCOUNTERS AND CONVERSATIONS.
Harper & Row, Publishers, Inc. 1971
With best wishes,
Alexey
чт, 9 мар. 2023 г. в 11:36, Richard Gill <gill...@gmail.com>:
Austin Fearnley
Quote from Richard:
"In my opinion, the phenomena explored in Bell type experiments cannot be *explained*. I used to find that extremely disturbing. But having thought about this for 30 years, I don’t have a problem with that right now. I’m prepared to change my mind if new theories come up or new data. I don’t think that retrocausality or super determinism is an *explanation* (sorry, Ben)."
I skimmed this morning through the more-immediately-accessible-to-me parts of Paul Raymond-Robichaud's recent paper on the Royal Society site. https://royalsocietypublishing.org/doi/full/10.1098/rspa.2020.0897#d1e14966
If I ever have a year to spare I will read it more extensively. I doubt that his conclusions are correct but I am in no position to make detailed comments on his paper after a quick skim. But some ideas were relevant to me...
Extract from Raymond-Robichaud's paper:
"At all times, the state of universe is described, up to irrelevant phase factor, by a unit vector in the Hilbert space of the universe, called the universal wave function of the universe. ..."
The key words which I have dwelt on are 'irrelevant phase factor'. Phase implies exponentials, and complex exponentials imply unitary, and this implies a cyclical or modular notion. In a statistical averaging over time and hence over phase, the phase is maybe irrelevant in a statistical theory where outcomes are probabilistic based on a modular repeating pattern together with an implicit randomness in the theory. But in a theory trying to capture event-at-a-time outcomes the phase is very important. (Doesn't Feynman use this phase to account for interference effects?)
This is connected with my classical gyroscopic model of an electron which uses both QM's say |up> and also phase, say, angle phi. This can be seen in my paper at
https://vixra.org/abs/2006.0160
This classical model predicts event-by-event outcomes of Malus's Law. The hidden variable phi (phase) for a given polarisation say |up> has to be generated randomly. It is a two stage process because a pure random vector phi points equally in all directions in an upper hemisphere, but this will not give Malus outcomes. My gyroscope does not point equally in all directions as it points in space vector up more than it points elewhere, and the probability falls off as phi points more and more to the horizontal.
I assumed a 2-D explanation by assuming symmetry (statistically, over time) of the gyroscope precession and nutation. This is because I knew about Chantal's simulations based on 3-D generations of random vectors on a sphere. My naive statement above that pure random vector phi points equally in all directions in an upper hemisphere is not true. One needs to generate phi in quite a complicated random process to obtain the random-on-a-sphere vectors. So I would need to do that first and subsequently amend phi to cater for phi being biased towards space vector up. Using 2-D removes that problem but still requires a two stage process to massage the random phi values, which I used in my computer program. If I ever have a few months to spare I could try to write the program with a 3-D randomisation algorithm.
But one can use Malus without extending oneself to use event-at-a-time outcomes. Just simple applications of Malus's Law can solve all Stern-Gerlach outcomes as far as I know. For use with electrons one has to modify Malus's formula from cos^2 (theta) to cos^2 (theta/2) to get the intensity measured at an angle theta to the incoming polarisation angle of the beam of electrons. So cos^(45/2) = 0.8535. This is notionally equivalent to a correlation of 0.707 between two space vectors separated by theta = 45 degrees.
In my opinion the value for the correlation of 0.707 above is akin maybe to violation of locality according to Bell's Theorem even though I am using a simple classical gyroscopic model. The violation is merely because the space vector phi is not distributed randomly in the upper hemisphere. But this is not a Bell experiment ... In my work over ten years on this I wearied of Bell deniers trying to prove that Bell's Theorem was incorrect and I distanced my mind from the Bell formula derivations (and left that in Richard's hands). Instead I concentrated on a simple angle between two vectors, which is the Malus experiment. A correlation of 0.707 is the very definition of the correlation between two static vectors separated by an angle of 45 degrees. But the projections onto the vector must be continuous values. If one rounds to the nearest integer then the correlation (using computer simulations is about 0.5). That discrepancy between discrete and continuous variable correlation allows me to accept the truth of Bell's Theorem without going into fine details of the proof. But does Malus Law contain the strangeness of obtaining a continuous variable correlation using integer variables? Not sure. I do not have to measure the incoming beam (afterwards) in a Malus experiment and I would not be measuring the correlation event-at-a-time. Yet I can obtain the maybe strange Malus effects using a classical gyroscopic model and without using retrocausality. But this use of Malus does not involve entanglement. The strangeness of Bell seems to be an additional kind of strangeness than that found in Malus and is caused by entanglement.
I opened with reluctance (I am trying to give up physics) my large file of lecture notes yesterday on Susskind's online lectures on entanglement and QM. I need to go through Pauli matrices and their eigenvectors, and the Born rule as I am querying the definitions of spin |up> and phase variables as I see the statistical nature of QM involving somehow statistical averaging over time over supposedly irrelevant variables. I probably need to see more on how the Pauli matrices apply in the more physical seeming space of geometric algebra as polarisation |up> is dynamic in my gyroscopic model and also is not a spatial vector.
A last point here is that using conservation of angular momentum makes me think that if a joint up&down is suddenly separated into individual up and down, then the separated up and down are matched for phase value in addition to polarisation vectors |up> and |down>. But the QM calculations only take forward the polarisation vectors in the calculations? Ignoring (if that is what really happens?) the phase aspects means that one cannot predict individual particle interaction outcomes. That is because CFD only applies if phase is taken into account. Using Malus Law to measure outputted intensities of beams can be used without simulating phi phase values. But in a Bell experiment to measure correlations, phi would seem to be a necessary input and it seems odd to me to expect a correlation of 0.707 using a model where only |up> and |down? polaristions are used. Sorry to sound like a Bell denier as I am not one. I said a few weeks ago that I was focusing on whether the problem lay in QM. I know that Richard can prove Bell's Theorem without using QM. So my issue is not with Bell but with QM claiming via entanglement to solve Bell. I have my own method to bypass Bell via retrocauslaity, rather than break Bell. I think it more realistic to try to bypass Bell's no go theorem rather than try to break it.
Austin
Richard Gill
Richard Gill
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/0ac3d24c-3047-414b-b932-d0c6b3d40eean%40googlegroups.com.
Austin Fearnley
Your post was a surprise to me. Maybe in response to my poor wording.
QM does not “solve” Bell.
So your theory may do wonderfully well at explaining what we think we understand about photons or electrons or whatever, but that does no way to explaining the data observed in certain experiments.
Richard Gill
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/6823d044-093a-42f4-ba29-cd42e2445316n%40googlegroups.com.
Richard Gill
On 10 Mar 2023, at 08:36, Mark Hadley <sunshine...@googlemail.com> wrote:
Dear Richard,A retro causal model has a chance to explain quantum theory (as does any contextual model). It could be a counterexample to BI. Just as the Bohm pilot wave is.The question is can such a model reproduce QM in a natural way.CheersMark
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/57F131FD-AC98-4876-AD77-973BB66DCF62%40gmail.com.
Jan-Åke Larsson
The big problem here is that retrocausation does not explain anything.
It does not explain how everyday events seems to obey standard causation, i.e., that cause precedes effect.
It does not explain how quantum correlations are bounded the way they are (yes, there are Bell-nonlocal models that are signal-local, that still reach the trivial algebraic upper bound of 4 in CHSH, a retrocausal model would be able to do that, for example).
You can reproduce any correlation.
This has a serious consequence: Retrocausal models are not falsifiable. A hypothesis is testable if there is a possibility of deciding whether it is true or false based on experimentation by anyone. You can't do that here.
So I would classify this as Not Even Wrong.
/Jan-Åke
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/04BC3334-EE86-4637-AD1D-9AC9BEBE28DB%40gmail.com.
Jan-Åke Larsson
Professor, Head of Department
|
|
|
Department of Electrical Engineering SE-581 83 Linköping Phone: +46 (0)13-28 14 68 Mobile: +46 (0)13-28 14 68 Visiting address: Campus Valla, House B, Entr 27, 3A:512 Please visit us at www.liu.se |
Austin Fearnley
Thank you for your post. It seems that I have some explaining to do which I had not realised was necessary. So thanks for nudging me to clarify. I am still surprised about these misunderstandings as I am sure that I have written about this before in blogs, including mine, and in vixra papers. I do not have the authority, unlike you, to say I have written this again and again etc. Though maybe I do not write it often enough and in the right papers. Apart from you I have only had one constructive feedback on my model from 'Mikko', which was very useful.
I started my simulations of a Bell experiment by trying to help Fred to make a computer program of Joy's 'one-page paper' model. That was probably back in 2011 or later. I have just used google search to find that one-page paper to see if my memory of his model was faulty but it seems to be the same. His pdf, though, is now dated 2015. My idea of a Bell experiment was fixed by that one-page paper though I have simplified my goal by usually fixing Alice's vector at 0 degrees and Bob's at 45 degrees and ignoring all other settings. This is the angle where the difference between the cosine curve and the sawtooth curve is greatest. I may have done this simplification because I am lazy but I prefer to think I am using Occam's razor to avoid unnecessary intricacies in the computer simulations.
Joy's papers in response to criticism moved on in complexity and I eventually applied the razor again and lost touch when it reached eight dimensions. (Somehow, though, my preon model uses at least 24 dimensions so I should not complain about use of a large number of dimensions.)
The design of Bell experiments also moved on. I lost touch/interest with developments when Charlie entered the scene and probably much earlier as Richard's blog posts were my main source of information on design of Bell experiments. My goal was a simplified, single settings, version of the Alice & Bob experiment in Joy's paper. I never went anywhere near the ABC trio design. I appreciate that the actual experimental designs need to have all the intricacies to avoid loopholes in real experiments. But my simple artificial simulations did not IMO need to have those intricacies. My goal was the simplest simulation, If I could not make that work then I would have no chance with a much more complicated design. I am not trying to close real loopholes in my artificial simulations. (Though it would be possible to try to do so if I had the energy/incentive, but my incentive has been to use the simplest design possible.)
To be clear, my model does not break the Bell Inequalities. As you often say that Bell's theorem doesn't solely apply to particle physics, I should point out that I cannot make a similar bypass of Bell's Theorem for macroscopic bodies as macroscopic bodies do not exhibit retrocausality in my model. It seems to be a criticism of retrocausal models that one does not see retrocausality in the macro world. Well, my model applies to micro only as one does not find macro bodies made of antimatter. My model also does not agree with Bell's Theorem as the flight paths of the particles do not conform to Bell's Theorem nor to the constriction of Bell's Inequalities. The particles are not entangled when the antiparticles are measured.
My simplification process also led me to start by replacing the full Bell situation by just having two unit vectors a and b separated by 45 degrees and finding the correlation between them using exact or continuous projections and then again by using integer projections. (See https://vixra.org/abs/1610.0327)
I used a = (0 ,0, 1) and b = (0, 0.707 ,0.707) and the angle between a and b is 45 degrees. (Particle) Vector e varies from pair to pair, chosen at random within a unit sphere, pointing out from the centre of the sphere and represents the particles.
When integer measurements A and B are correlated, the correlation is 0.499374804 with one million pairs of particles. When the continuous variable values (via exact projections) of A and B are used then the correlation is 0.707000432.
This is the simplified circumstances that I have worked with in my simulations. I know it is not exactly the full 'Bell'. Maybe I should call it the fuzzy correlation attentuation problem. 'Bell' is very useful as it formally sets out the BIs. I have not been able to prove theoretically that the fuzzy (or discrete projections) correlations in my scenario are limited to 0.5, for theta = 45 degrees, but that is what I find in computer simulations. So I do appreciate Bell for setting formal limits as I cannot do that formally for my simplified design.
My retrocausal paper at https://vixra.org/abs/2205.0140
applies retrocausality to this simple simulation design and obtains the correlation of 0.707 with fuzzy or integer measurements. This corresponds to a bypassing of Bell's Theorem as Bell's Theorem does not apply to my retrocausal design. However, the design appears to be similar in essence to a Bell experiment and I ought to be able to apply my retrocausal model with success to a more complicated Bell design. If that is the case then that would indicate that real Bell experiments also can obtain the 0707 correlation by bypassing the Bell Inequalities.
My paper uses the statistical Malus's Law and so is not particle-at-a-time. In a previous forum discussion somewhere with Richard, he asked me to make a particle-at-a-time simulation so that he could more accurately categorise how my model failed to break the Bell Inequalities. I hope people can see that was not an inspiring suggestion for me. I do have a computer program listing online in the appendix of https://vixra.org/abs/2006.0160 . That program could be used to turn my recent paper into a particle-at-a-time simulation. That program reproduces Malus Law outcomes and Stern Gerlach outcomes so I have no doubt that I could with some effort help Richard to classify how my model fails. That program uses a 2-D algorith and again I have no doubt that with some more effort I could turn that into a 3-D design and make an even more fancy simulation.
But IMO my model successfully obtains, by using retrocausality, a fuzzy (or integer variable) correlation of 0.707 for unit vectors separated by 45 degrees. To me that is the essence of Bell even if not exactly same thing. It is very strange that a continuous-variables correlation of 0.707 is necessarily attenuated into a 0.5 correlation by using fuzzy or rounded-to-the-nearest-integer measurements, any yet some model or other can reverse this and get back the 0.707 correlation, that is to disattenuate the correlation, while still using fuzzy variables. That ought to be no-go territory. Retrocausality can do this but it is a strange idea. QM can also do this and experts are saying that it is not strange? I suspect that retrocausality will have uses.
Finally, rest assured Richard that I am not claiming that retrocausality breaks Bell's Theorem nor agrees with it. It bypasses it. Not sure where that leaves your table of categories of failure of models. Timing of measurements is not an issue in my model as entanglement is not used, nor is detector setting bias relevant here, nor any restrictions about particle polarisations, and probably not anything else that affects real experiments but do ask me about specific issues in the design if you like.
Austin
Richard Gill
On 10 Mar 2023, at 15:12, Mark Hadley <sunshine...@googlemail.com> wrote:I agree with most of that. I'm using counterexample in a slightly different way.Any explanation will indeed look crazy. It will inevitably be a relaxation of causality. But if a simple universal principle comes forward that can be used to derive quantum theory, then it will be accepted. And yes it will have to make new testable predictions.The good news is that QM equations are the ONLY way to put a consistent probability structure on a context dependent theory.My own work is on 4 geons. I prove that the probabilities must be like QM in principle. My new predictions are no graviton and that Parity is conserved. What I lack is a microscopic detail of what happens in quantum experiments. But imagine proving the probabilistic outcomes of a dice throw from first principles.See:Www.DrMark Hadley.comCheersMark
Mark Hadley
Mark Hadley
To view this discussion on the web visit https://groups.google.com/d/msgid/Bell_quantum_foundations/57F131FD-AC98-4876-AD77-973BB66DCF62%40gmail.com.
Inge Svein Helland
Dear all.
Can one find a new foundation of quantum theory, a foundation which ultimately leads to the full theory, but at the same time a foundation which can be explained also to persons that never have been exposed to the ordinary Hilbert space machinery?
My answer is yes. I have tried to discuss my approach in a book and in several published papers. Now I have collected all the mathematical arguments in a single article, attached here. It is not necessary to read this article, however. I will explain my model and some of my main results below.
Some background: Jim Al-Khalili from Surrey and I are guest editors for an issue of the journal Universe on the topic ‘Approaches towards Quantum Foundation’. This article is submitted to Universe as my Feature Article.
My basic notion is that of a variable. A variable can be a physical variable, a statistical parameter, a future data variable, a decision variable, or perhaps also other things. I divide the variables into accessible ones and inaccessible ones. Physical variables are accessible if we by some measurement can get as accurate values as we want to. In general, I only require that if theta is accessible and lambda is a function of theta, then lambda is also accessible. In a measurement situation the notions accessible/ inaccessible may be connected to the mind of some observer/actor or to the joint minds of a communicating group of actors.
Some examples:
1) Spin of one particle. An observer A can have the choice between measuring the spin in the x direction or in the z direction. This gives two related accessible variables in the mind of A. An inaccessible variable is the unit spin vector phi. In the qubit case, the spin component in any direction a is a simple function of phi: sign(cos(a,phi)), taking the values -1 or +1.
2) The EPR situation with Alice and Bob. For an independent observer Charlie, the unit spin components of both are inaccessible, say n_A and n_B. But it can be shown that the dot product of the two is accessible to Charlie: d =n_A . n_B. Specifically, one can show that Charlie is forced to be in an eigenstate for the entangled singlet state corresponding to d=-1. It is easy to show that this implies that for Charlie and for the measured components in some fixed direction a, the component of Alice is opposite to the component of Bob. Note that Charlie can be any person.
3) The Bell experiment situation. Look at the subsample of data where Alice measures her spin component in direction a and gets a response A, either -1 or +1, and where Bob measures in a direction b and gets a similar response B. Then A is accessible to Alice, but inaccessible to Bob. Similarly, B is accessible to Bob and inaccessible to Alice. For an independent observer Charlie, having all data, both A and B are accessible. But Charlie has his limitation as in 2) above, and this implies by Born's formula – anticipating this formula, for which a long series of arguments can be given - a fixed joint distribution of A and B. Again, Charlie can be any person. I have a paper on what this limitation implies for him, using my point of view.
4) The Monty Hall problem. An actor A opens a door, and gets a reward X. This reward is inaccessible to him before the door is opened, but accessible afterwards. His main problem is that he does not know anything about the state of the host and how he uses his knowledge. According to the Wikipedia article about Monty Hall there exists a quantum version. This has to do with the situation where A knows his X_1 after he has opened one door but does not know his X_2 after he has two choices, either keep his original choice or switch door. His inaccessible phi is the knowledge of the host.
5) A general decision problem with two alternatives. In the simplest case the actor A knows the consequences of both choices, they are accessible. But in more complicated cases, the consequences are inaccessible, and hence the consequence of his choice is inaccessible. Then an option can be to make a simpler sub-decision, where he knows the consequences.
All these examples can, I think, be coupled to my approach towards QM. I will now sketch the basic elements of this approach.
My point of departure is a statement of Hervé Zwirn’s Convivial Solipsism: Every
description of the world must be relative to the mind of some observer. Different
observers can communicate. A consequence of this is that physical variables also must
be assumed to have some ‘existence’ in the mind of an observer. In the following I will
take as a point of departure a concrete observer A. This will be assumed throughout
the following arguments but note that A can be any person.
Postulate 1: Assume that A is in some (physical) context. Every (physical) variable in
this context has a parallel existence in the mind of A.
The variables may be accessible or inaccessible to A. If theta is accessible,
A will, in principle in some future be able to find as accurate value of theta as he
likes. This is taken as a primitive notion. From a mathematical point of view, I only
assume:
Postulate 2: If theta is accessible to A and lambda= f (theta) for some function f , then lambda is also accessible to A.
The crucial model assumption is now the following:
Postulate 3: In the given context there exists an inaccessible variable phi such that
all the accessible ones can be seen as functions of phi.
In general, this postulate, taken together with some symmetry assumptions,
has far-reaching consequences. And these symmetry assumptions will be
shown to be satisfied in important cases, for instance when all accessible variables take
a finite number of values.
Now I introduce a partial order among my variables: lambda is less than or equal to theta if lambda=f(theta) for some function f. If theta is accessible and lambda is less than or equal to theta, then I assume that lambda is accessible.
Postulate 4: There exist maximal accessible variables relative to this partial ordering. For every accessible variable lambda there exists a maximal accessible variable theta such that lambda is a function of theta.
This can be motivated by using Zorn’s lemma and Postulate 3, but such a motivation is not necessary if Postulate 4 is accepted. Physical examples of maximal accessible variables
are the position or the momentum of some particle, or the spin component in some
direction.
These 4 postulates are all that I assume. Through some mathematical arguments I can prove in the case of variables taking a finite number of values:
Theorem: Assume that there relative to the mind of an observer A in some given context among other variables exist two different maximal accessible variables, each taking n values. Then there exists a n-dimensional Hilbert space H describing the situation, and every accessible variable in this situation will have a unique self-adjoint operator in H associated with it.
This is my starting point for developing the quantum formalism from simple postulates. Using the same 4 postulates in the finite-dimensional case, further results can be proved, among other things:
- The eigenvalues of the operator associated with theta are the possible values of theta.
- The accessible variable theta is maximal if and only if all eigenvalues are simple.
- The eigenspaces of the operator associated with one of several variables, say theta. are in one-to-one correspondence with questions of the form ‘What is theta/ what will theta be if it is measured?’ together with sharp answers ‘theta=u’ for some u. In the maximal case this gives a simple interpretation of eigenvectors.
Note that my approach here is fully epistemic. It has to do with an agent seeking knowledge. In the finite-dimensional case we may concentrate on state vectors that are eigenvectors of some meaningful operator. If this operator is associated with a maximal accessible variable theta, then in general these state vectors have interpretations as questions-and-answers as above.
To show this requires some mathematics, given in the attached article, where also a further discussion is given. What is lacking here, are arguments for the Schrödinger equation and for the Born formula from simple assumptions. I refer to my Springer book for these topics, but the Born formula is discussed in the attached article.
The discussion above was limited to the mind of a single observer A. Now the same mathematics applies to the following situation: There is a group of communicating observers, and jointly accessible or inaccessible variables in some context are associated with the group.
Note that in this whole discussion I have said nothing about the ontology. I am fully convinced that there exists an external world, but the detailed properties of this world may be outside our ability to find out. And QM as a model, although it is a very good model, can sometimes only give partial answers.
What I miss now, is some discussion around the above approach. I admit that the approach is unusual and that the postulates may seem a little abstract. However, for an outsider I will claim that it is much easier to understand these postulates than jumping right into the usual Hilbert space formalism. For those of us who have learned the formalism, the approach may in some sense require some unlearning first.
Inge
