YALMIP and GUROBI for trajectory optimization

[Corbin Wilhelmi]

All,

First off, Johan (if you are reading this), thank you so much for this program, it has made my life vastly easier.  The tutorials were fantastic, that being said:

One question that I have not seen in these question posts...

I am working on a receding horizon trajectory planner for an autonomous aerial vehicle.  I have all of my constraints (such as speed, angles, control stability, state space, collision avoidance, etc) listed as instructed.  What I cannot figure out is how to tell it a location that I want to go to.  I have figure out all of the hard stuff except how to go from "A" to "B".  I am sure that this sounds simple but it's driving me nuts. 

Any help on where to put it in will be appreciated. 

Code available upon request.

Thank you all for your time and consideration.   

Best
Corbin

[Johan Löfberg]

Not sure what you mean. If you have a state-space model where some states Cx(t) reflect position, then you would simply start from some initial state where Cx(t) happens to be equal to A, and you ewant to go to B, i.e, the term B-Cx should enter the objective function somehow, or perhaps even a terminal state equality Cx(t+N)=B

[Corbin Wilhelmi]

Johan,

Let's say that I have a quadcopter / helicopter sitting at [X(0), Y(0), Z(0)] and let those be points (0,0,0) in Cartesian coordinates.  Assume that the object of the drone is to get to point at final time T, [X(T), Y(T), Z(T)] and let those points be (100,100,100).  For fun, let's add obstacles at (50,50,50), (25,50,50) and (75,50,50).  I used the "Big M" technique as a function of velocity to determine the larger size of the box.  Using MPC / receding horizon, I need to develop a trajectory based upon some number of time steps. 

Constraints:
 - x(k+1) = Ax(k) + Bu(k) + disturbance; where disturbance = 0;
 - y(k) = Cx + D; where D is a zero vector
 - Sizes and locations of obstacles
 - Angular Velocity constraints
 - Angle constraints
 - Acceleration constraints

I just am not sure of where to put in the final position as the ultimate goal. 

Again, thank you for your time and consideration.

Best
Corbin

[Johan Löfberg]

if x denotes [X;Y;Z], you want to penalize the distance to T=[100;100;100] somehow. For instance, by minimizing sum (x(k)-T)'*(x(k)-T) along the prediction horizon, or the 1-norm etc.

Last example in this
http://users.isy.liu.se/johanl/yalmip/pmwiki.php?n=Blog.Minicourse-material

[Corbin Wilhelmi]

Thank you so much, that makes a lot of sense.  If I have any more questions I will post them here. 

Also, do you have the information available to cite the conference? 

Best
Corbin

[Johan Löfberg]

no, there is nothing to cite here. just bulk material as the rest of the wiki examples

[Corbin Wilhelmi]

Using your robotmpc*.m codes I have been able to manipulate them in order to do what I need them to be able to solve; however, I am having some trouble adding in one constraint.

Let's assume that there is an object in the way with vertices of (-1,1),(-1,-1),(1,-1),(1,1).  Using your C matrix and X vector from your course:

C = [
0 1 0 0;
0 0 0 1 ] ;

X1 = x velocity; X2 = x location; X3 = y velocity; X4 = y position;

Let k = time or sample

I am trying to write the constraint as follows (of course with others, but for space considerations):

constraints = [ ];
constrains = constraints + [( ... % Open the constraint possibilities
     (C(1,2) * x{k}(2) > 1) + ... % Allows for all possibilities on the x axis to be greater than the largest x vertex
     (C(1,2) * x{k}(2) < -1) + ... % Allows for all possibilities on the x axis to be less than the smallest x vertex
     (C(2,4) * x{k}(4) > 1) + ... % Allows for all possibilities on the y axis to be greater than the largest y vertex
     (C(2,4) * x{k}(4) < -1) ... % Allows for all possibilities on the y axis to be less than the smallest y vertex
     ) ... % Close the constraint possibilities
     <= 3 % If one of the above is not satisfied then the robot is not in the obstacle
];

When I do this, along with other constraints that work (when this is taken out), I come up with the following error:

Undefined function 'le' for input arguments of type 'lmi'. 

Google has proven to be unhelpful.  If you have any ideas or a better way to write this constraint please let me know.

Best
Corbin

[Corbin Wilhelmi]

Also, while continuing to experiment I am running into an issue with your optimizer command.  For instance, I am changing your code into a three dimensional problem (for real world issues). 

Here is the code:

A = [1 0 0 0 0 0; .1 1 0 0 0 0; 0 0 1 0 0 0; 0 0 .1 1 0 0; 0 0 0 0 1 0; 0 0 0 0 .1 1];
B  = [.1 0 0; .005 0 0; 0 .1 0; 0 .005 0; 0 0 .1; 0 0 .005];
C = [ 0 1 0 0 0 0 ; 0 0 0 1 0 0 ; 0 0 0 0 0 1];

nu = size(B,2);
nx = size(A,1);

Q = eye(3);
R = .1*eye(3);
N = 10;

u = sdpvar(repmat(nu,1,N),repmat(1,1,N));
x = sdpvar(repmat(nx,1,N+1),repmat(1,1,N+1));

constraints = [];
objective = 0;
for k = 1:N
    objective = objective + norm(C*x{k},1)+norm(R*u{k},1);
    constraints = [constraints, x{k+1} == A*x{k}+B*u{k}];
    constraints = [constraints, -2<C*x{k}<2,-1<u{k}<1];
end


% Plot the playing field and regions to avoid.
clf
plot(-2 < C*x{1} < 2,[],'FaceAlpha',0);hold on
plot(norm(C*x{1}+[.2;-.3;.4],inf)<0.2);
plot(norm(C*x{1}+[-.2;0.3;.2],inf)<0.2);
plot3(0,0,0,'.b','MarkerSize',50)
axis([-2 2 -2 2 -2 2]);

controller = optimizer(constraints,objective,[],x{1},u{1});

count = 1;
x_(:,count) = [ -2 ; .27 ; -2 ; .4184; -2; .9977]


while norm(x_(:,count)) > 1e-2
    drawrobot(x_(:,count));
    u_(:,count) = controller{x_(:,count)};
    x_(:,count+1) = A*x_(:,count)+B*u_(:,count);
    count = count+1;
    pause(.01)
end

I am getting an error in the "WHILE" loop at the controller{x_(:,count)} command.  I instituted a count variable in order to store the values throughout the simulation just for sanity checking later. 

Any ideas?

Best
Corbin

[Johan Löfberg]

A constraint does not automatically generate an indicator if that is what you are trying to do. A+B where A and B are constraints is simple the intersection [A,B], and you cannot compare a constraint with a value. I.e, you are defining a polytope, and then saying that the set defining the polytope should be less than 4!? You have to do logic modelling manually

http://users.isy.liu.se/johanl/yalmip/pmwiki.php?n=Tutorials.Big-MAndConvexHulls
http://users.isy.liu.se/johanl/yalmip/pmwiki.php?n=Tutorials.LogicProgramming

E.g.,

d = binvar(4,1);

 [implies(d(1), (C(1,2) * x{k}(2) >= 1)),
  implies(d(2), (C(1,2) * x{k}(2) <= -1)),  
  implies(d(3), (C(2,4) * x{k}(4) >= 1)),
  implies(d(4), (C(2,4) * x{k}(4) <= -1)),
  sum(d)>= 1];

As you can see on the Wiki, you can use OR operators etc, but I advice against that at the moment (known bugs, fixed in next version, but primarily as it hides the MILP formulation. You should know what you are doing)

[Johan Löfberg]

Isn't YALMIP screaming at you to stop using strict inequalities? Listen to that advice (the code is old...)

I can only assume that the solve fails, thus leading to x being nan or something like that

    [u_(:,count),diagnostics] = controller{x_(:,count)};
    if diagnostics
        yalmiperror(diagnostics)
        error('FAIL!');
    end

[Johan Löfberg]

As you haven't explicitly selected the solver, you should check that you actually have a good solver detected

>> controller
Optimizer object with 6 inputs and 3 outputs. Solver: GUROBI-GUROBI

[Corbin Wilhelmi]

Johan,

I read through and did the examples in the Wiki, they are really helpful.

I am now seeing a new error in the "implies".  I have attached the code for your convenience and commented every line so you can see my train of thought.  This might be part of the bug you mentioned, I'm not sure.

Thanks for your help.  If I get this part figured out, I can stop bugging you.  I'm used to doing numerical optimization for other uses, MPC is a new field that I am studying and this is the best source I have found. 

Best
Corbin

[Johan Löfberg]

Some of your constraints evaluate to 0 (since model.C(1,4) is zero)

>> model.C(1,4) * x{k}(4) >= (max(obstacleLocation{j}(:,2)))

ans =

     0

YALMIP then gets lost when you say that variable implies 0

BTW, you are currently using the same d along the whole trajectory. That does not make sense

[Johan Löfberg]

not only are you using the indicator binaries for all time instances, you are using the same indicators for all obstacles too. You need one binary for every hyper-plane of every obstacle at every time-instant. Some of the indicators for an obstacle has to be non-negative, for all obstacles and all time-instances.

[Corbin Wilhelmi]

So I fixed both of those issues, the first was a typo and the second is a good point that your brought up.  Everything seems to be working now except that it will not track to the origin (0,0) as it does in your examples.  At this point, I'm just excited that it runs.  If you look at the same code, any ideas why it doesn't track correctly? 

Best
Corbin

[Johan Löfberg]

show the fixed code

[Corbin Wilhelmi]

Please see attached for the fixed code. 

[Johan Löfberg]

too short horizon

[Johan Löfberg]

and the model is still flawed, as you are using the same indicators along the whole trajectory. This means that you are saying that one of the hyperplanes has to be violated along the whole trajectory. I'm trying to understand how it even can be feasible, but it is clearly a flawed model

EDIT: Understand how it can remain feasible. It simply means the solution in every solve is conservatively constrained to behave in a very specific manner (the predicted trajectory must remain on one side of a hyperplane along the whole prediction, meaning it won't engage in planning cornerering until it has passed a hyperplane)

controller = optimizer(constraints,objective,[],x{1},{u{1},[x{:}]}); % Develop The Controller

timeStep = 1; % Count Number Of Steps To Reach Final Convergence
x_(:,timeStep) = randominitialpoint; % Original Starting Point And Velocities

%% Plot Final Result
clf
axis([-2 2 -2 2]);
hold on
for i = 1:obstacles % Plot The Obstacles
    fill(obstacleLocation{i}(:,1)',obstacleLocation{i}(:,2)','r');
end
hold on
while timeStep < 500 %norm(x_(:,timeStep)) > 1e-2 % Convergence Constraint Loop
    sol = controller{x_(:,timeStep)}; % Optimize The Problem
    u_(:,timeStep) = sol{1};
    xx = sol{2};
    plot(xx(2,:),xx(4,:));drawnow;pause(0.1);
    x_(:,timeStep+1) = model.A*x_(:,timeStep)+model.B*u_(:,timeStep); % Find New Information Based On State Space Equation
    timeStep = timeStep + 1; % Increment The Time Step
end

[Corbin Wilhelmi]

Correct.  Right now it is very conservatively constrained.  The only issue that I am currently working through is how to tell it what "direction" the robot is facing.  Any ideas on this?  Some sort of rotational matrix from the world body to the robot body?  I have this already just not quite sure where to enter it. 

I am working through a final test of a 3d version of the optimization algorithm, will post results when finished as well as code for others to use as needed. 

I'll run your new code in a little bit and report on the results.  I am currently running a simulation with ~150000 constraints. 

[Johan Löfberg]

OK, so you mean the weird same-indicator-at-all-samples is not accidental?

The model you have is a point-model, so there is no concept of direction (except that the particle moves in a direction, which would be the physical direction in practice)

[Corbin Wilhelmi]

I am assuming that you are talking about the 'd' value in the constraints.  Right now, I want it to be able to a priori knowledge of the entire platform.  Later, it will only have limited knowledge of what is going on. 

Is there a way to change it from a point model to one where I can input initial direction?

[Johan Löfberg]

Don't understand what you mean about a-priory knowledge. What I am saying is that the code logically should be something like implies(d{k,obstacleindex}(hyperplaneindex), ...), sum(d{k,obstacleindex})>=1

I have never worked with more complex models. I think they get ugly rather soon as you seem to want to introduce rotations, which is a nonlinear construct.

[Corbin Wilhelmi]

They do get pretty ugly really quick.  I am having to build in various loops based around the constraints that I have at different points of time in "flight". 

a priori - advanced knowledge. 

I do need to find a way to optimize your optimizer command.  Is there a way to parallel process it?  I'm running on a 12 core i7 with 64gb ram and two hard drives (256 ssd, 2tb mechanical)

[Johan Löfberg]

Do you mean making the command optimizer faster, or reducing the overhead in optimizer, or actually solving the problem? If you mean actually solving the MIP, you will start to invest (massively) in improving the model by adding cuts on the binary variables etc from a-priori knowledge.

[Corbin Wilhelmi]

Solving the problem is actually incredibly fast, even with 200,000+ constraints it will solve each iteration in ms.  It is the the original overhead set-up: controller = optimizer(constraints, objective, [], x{1}, u{1}).  When I run the actual experiment the constraints will be closer to 10,000, just trying to push the limits right now for future knowledge.

As soon as my computer frees up I'll post my 3D code here.  What I am currently finding with horizon = 100, is that when starting with any coordinate being positive, the optimizer is not able to converge to the origin.  In fact, it actually goes the opposite way like you expect in a Trust Region analysis with a negative Hessian value.  Thoughts on this?  I'm currently running with horizon = 500 to test it out and see if that is an issue. 

[Corbin Wilhelmi]

This is set-up with a horizon or 75.  I ran it with a horizon of 500 and it made no difference in the final result.

In line 277 (or around there depending on how you load the .m file) you can pre-set the starting position.  If you set any of the three cartesian coordinates (x,y,z) to a positive number, the optimization fails.  Thoughts? 

[Johan Löfberg]

I can only guess that it is an effect of your weird constraint that the initial state completely defines which constraints have to be violated along the whole predicted trajectory, due to your definition of d. This is probably also the reason it is so easy to solve the problem. Basically, all constraints which aren't violated in the initial state, must stay unviolated along the whole trajectory (this cuts the search space a lot), and the initial state directly defines the set of initially violated constraints, of which some must remain violated along the whole trajectory, once again cutting down the search space.

[Johan Löfberg]

You mean it always fails? It fails sometimes, which is natural as it should happen sometimes that the starting point is inside an obstacle thus leading to infeasibility

   [u_(:,timeStep),problem] = controller{x_(:,timeStep)}; % Optimize The Problem
    if problem
        yalmiperror(problem)
    end

As for performance, the version you have now can be vectorized completely

[x{2:end}] == model.A*[x{1:end-1}]+model.B*[u{:}],
-1 <= [u{:}] <= 1,

...
X = [x{k}];
implies(d(obstacleCount), model.C(1,2) * X(2,:) >= (max(obstacleLocation{j}(:,1)))),
etc

[Johan Löfberg]

BTW, looking at the original model you had

constrains = constraints + [( ... % Open the constraint possibilities
     (C(1,2) * x{k}(2) > 1) + ...

     (C(1,2) * x{k}(2) < -1) + ...

     (C(2,4) * x{k}(4) > 1) + ...

     (C(2,4) * x{k}(4) < -1) ...
     ) ... % Close the constraint possibilities
     <= 3 % If one of the above is not satisfied then the robot is not in the obstacle
];

Is this the type of model you want? I am a bit worried that we are talking past each other here. The model you have implemented now, does not implement this. In other words, with your k-independent definition of d, you are not saying (x{k} not in BOX1) and (x{k} not in BOX2) .

[Corbin Wilhelmi]

The way that it is coded is that the robot position is not in any box.

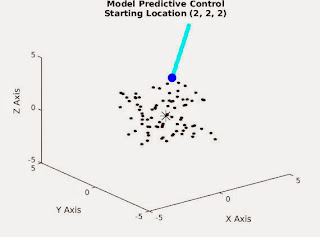
When I say fail I mean that it is moving away from the origin.  See embedded image here:

The starting point is not in any obstacle.  When in 3 dimensions the robot will move out into "space" and not towards the origin, this does not seem to occur in two dimensions.  If the starting point (in this example) is placed at the point (0<.5, 0<.5, 0<.5) then it will converge to the origin. 

Let me work through some of the actual math offline and I will post more this weekend. 

[Johan Löfberg]

But this simulation has been done without error checks, right? Most likely, you've run into infeasibility and the solver has returned 0, and then the robot just drifted away.

Placing it in the wrong position, combined with an initial velocity vector pointing outwards, should lead to infeasibility in many places

[Corbin Wilhelmi]

I didn't even think about the velocity vector.  Good call. 

[Carlos Massera FIlho]

Hi Corbin,

Just a design tip.

When designing your system contraints you should think of it as a Envelope Control, making sure that for every possible state within the constraints there is a control input that makes x_k+1 be within the contraints. 

This avoids your system to be unstable while x0 is still in the feasible set.

[Johan Löfberg]

So how would you do that? Already the convex LTI case is pretty tricky when it comes to guaranteeing recursive feasibility, forcing us to find an invariant set in which we know of a nominal control law which is feasible and keeps the state in the invariant set.