How to use a spline fit as driving function?
64 views
Skip to first unread message
willigott
Apr 26, 2020, 9:17:26 AM4/26/20
to tellurium-discuss
Hi all,
I am wondering whether there is a straightforward way to solve the following problem; would be great if you could take a look and give advice, thanks! I also attached the file with relevant code.
Let's say I have a model and would like to use a driving function, I can do:
import tellurium as te
import pandas as pd
import matplotlib.pyplot as plt
r = te.loada("""
model dummy()
# Inject sin wave into model
Xo := sin (time*0.5) + 2;
# Model Definition
v1: $Xo -> S1; k1*Xo;
v2: S1 -> S2; k2*S1;
v3: S2 -> $X1; k3*S2;
# Initialize constants
k1 = 1.0;
k2 = 1.0;
k3 = 3.0;
S1 = 3.0;
S2 = 0.0;
X1 = 0.0;
end
""")
r.exportToSBML('dummy_model_spline.xml')
result = r.simulate(0, 100, 1001)
df = pd.DataFrame(result, columns=result.colnames)
df.set_index('time').plot()
# "true" data; I don't know this function
x = np.linspace(0, 100, 1000)
d = np.sin(x * 0.5) + 2 + np.cos(x * 0.1)
# sample data; that's what I actually measured, experimental data
x_sample = x[::50]
d_sample = d[::50]
# fit spline
s = UnivariateSpline(x_sample, d_sample, k=3, s=0.005)
# # just to check
# xfit = np.linspace(x_sample.min(), x_sample.max(), 200)
# plt.plot(xfit, s(xfit))
I am wondering whether there is a straightforward way to solve the following problem; would be great if you could take a look and give advice, thanks! I also attached the file with relevant code.
Let's say I have a model and would like to use a driving function, I can do:
import tellurium as te
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import UnivariateSpline
model dummy()
# Inject sin wave into model
Xo := sin (time*0.5) + 2;
# Model Definition
v1: $Xo -> S1; k1*Xo;
v2: S1 -> S2; k2*S1;
v3: S2 -> $X1; k3*S2;
# Initialize constants
k1 = 1.0;
k2 = 1.0;
k3 = 3.0;
S1 = 3.0;
S2 = 0.0;
X1 = 0.0;
end
""")
r.exportToSBML('dummy_model_spline.xml')
result = r.simulate(0, 100, 1001)
df = pd.DataFrame(result, columns=result.colnames)
df.set_index('time').plot()
plt.show()
That works perfectly fine, but requires me to know the driving function (here: a sin function).
How could I now feed in an arbitrary input based on a spline function (if I have some experimental data and do not know the underlying model for it)? For example:
x = np.linspace(0, 100, 1000)
d = np.sin(x * 0.5) + 2 + np.cos(x * 0.1)
# sample data; that's what I actually measured, experimental data
x_sample = x[::50]
d_sample = d[::50]
# fit spline
s = UnivariateSpline(x_sample, d_sample, k=3, s=0.005)
# # just to check
# xfit = np.linspace(x_sample.min(), x_sample.max(), 200)
# plt.plot(xfit, s(xfit))
# plt.show()
is there now a way to feed this to the model, so something like:
Xo := s(time);
The s(time) of course will not work, one would need to translate this into a piecewise function, I guess.
Would you know how to do this?
Would you know how to do this?
Herbert M Sauro
Apr 27, 2020, 1:00:07 PM4/27/20
to willigott, tellurium-discuss
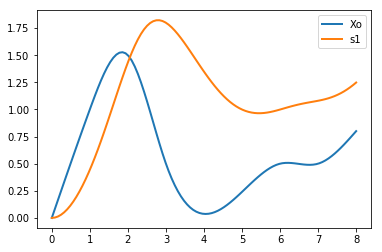
It is possible to include a spline function in your model to input an arbitrary function but it has to be input as a series of piecewise functions, for example:
import tellurium as te
import roadrunner
r = te.loada("""
Xo := piecewise (((-0.019175*(time-0) + 0.000000)*(time-0) + 1.019175)*(time-0) + 0.000000, (time >=0.000000) && (time <= 1.000000),\
((-0.404123*(time-1) - 0.057526)*(time-1) + 0.961649)*(time-1) + 1.000000, (time >=1.000000) && (time <= 2.000000),\
((0.635668*(time-2) - 1.269895)*(time-2) - 0.365772)*(time-2) + 1.500000, (time >=2.000000) && (time <= 3.000000),\
((-0.101418*(time-3) + 0.637107)*(time-3) - 0.998560)*(time-3) + 0.500000, (time >=3.000000) && (time <= 6.000000),\
((0.189856*(time-6) - 0.275654)*(time-6) + 0.085798)*(time-6) + 0.500000, (time >=6.000000) && (time <= 7.000000),\
((-0.097971*(time-7) + 0.293914)*(time-7) + 0.104058)*(time-7) + 0.500000, (time >=7.000000) && (time <= 8.000000))
J1: $Xo -> s1; k1*Xo;
s1 -> ; k2*s1;
k1 = 1; k2 = 0.4
""")
#te.saveToFile ('c:\\tmp\\spline.xml', r.getSBML());
m = r.simulate (0, 8, 100, ['time', 'Xo', 's1'])
r.plot()
import tellurium as te
import roadrunner
r = te.loada("""
Xo := piecewise (((-0.019175*(time-0) + 0.000000)*(time-0) + 1.019175)*(time-0) + 0.000000, (time >=0.000000) && (time <= 1.000000),\
((-0.404123*(time-1) - 0.057526)*(time-1) + 0.961649)*(time-1) + 1.000000, (time >=1.000000) && (time <= 2.000000),\
((0.635668*(time-2) - 1.269895)*(time-2) - 0.365772)*(time-2) + 1.500000, (time >=2.000000) && (time <= 3.000000),\
((-0.101418*(time-3) + 0.637107)*(time-3) - 0.998560)*(time-3) + 0.500000, (time >=3.000000) && (time <= 6.000000),\
((0.189856*(time-6) - 0.275654)*(time-6) + 0.085798)*(time-6) + 0.500000, (time >=6.000000) && (time <= 7.000000),\
((-0.097971*(time-7) + 0.293914)*(time-7) + 0.104058)*(time-7) + 0.500000, (time >=7.000000) && (time <= 8.000000))
J1: $Xo -> s1; k1*Xo;
s1 -> ; k2*s1;
k1 = 1; k2 = 0.4
""")
#te.saveToFile ('c:\\tmp\\spline.xml', r.getSBML());
m = r.simulate (0, 8, 100, ['time', 'Xo', 's1'])
r.plot()

The above line was generated using a plugin from pathwaydesigner but it should be possible to construct the same piecewise expression using python.
Herbert Sauro
--
You received this message because you are subscribed to the Google Groups "tellurium-discuss" group.
To unsubscribe from this group and stop receiving emails from it, send an email to tellurium-disc...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/tellurium-discuss/28b54a8e-dfcb-4139-bf08-04a295150486%40googlegroups.com.
Herbert Sauro, Professor
University of Washington, Bioengineering
willigott
Apr 28, 2020, 2:10:16 PM4/28/20
to tellurium-discuss
Thanks a lot for the reply! I will try this approach then.
To unsubscribe from this group and stop receiving emails from it, send an email to telluriu...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/tellurium-discuss/28b54a8e-dfcb-4139-bf08-04a295150486%40googlegroups.com.
Herbert M Sauro
Apr 28, 2020, 5:15:51 PM4/28/20
to willigott, tellurium-discuss
I put together this simple python script that can be used to generate the spline code for an antimony model.
The data are stored in xm and ym arrays, after that, it computes the spline and plots out the solution to make sure it looks ok, then it constructs the antimony string. You can then copy the spine string into the model and run it again, this time the model will respond according to the spline fit.
The code could be tidied up but it downs the job. If you find that you get convergence eros from the cvode integrator its because the spline is going something odd, like going negative etc. If that happens you have to adjust the data or using a different kind of interpolation.
Herbert Sauro
To unsubscribe from this group and stop receiving emails from it, send an email to tellurium-disc...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/tellurium-discuss/2fd9bcb6-48f7-4884-8b21-ee3803b6ee36%40googlegroups.com.
Reply all
Reply to author
Forward
0 new messages
