Priors for Mixed Effects Negative Binomial Model in Stan
1,386 views
Skip to first unread message
Jason Tilley
Jan 15, 2016, 11:09:08 AM1/15/16
to stan-...@googlegroups.com
So I successfully created my first mixed effects Gaussian model with STAN. It compiled and gave good results. Now I am trying to change the model to model a negative binomial response. The model compiles but fails to converge. I haven't found much about the proper priors for the neg_binomial(alpha, beta) function. But alpha obviously needs to be greater than zero, and beta should be bounded between 0 and 1. The conjugate prior of the negative binomial distribution is the beta distribution, and this seems to fit those criteria nicely. However, I get the following errors:
I think I might have my priors wrong, but then again it could be my linking function. I've spent a fair amount of time on this so far. Does anyone have any suggestions? Below is my code. Thanks.
stan::math::neg_binomial_log: Shape parameter is 0, but must be > 0!
Error in function boost::math::lgamma<long double>(long double): Evaluation of lgamma at 0.
I think I might have my priors wrong, but then again it could be my linking function. I've spent a fair amount of time on this so far. Does anyone have any suggestions? Below is my code. Thanks.
model_code = """ data { int<lower=0> N; //rows of data int<lower=0> K; // number of covariates int<lower=0> J; // number of groups matrix[N,K] x; // design matrix (predictors) int y[N]; // response (outcomes) int<lower=1, upper=J> groups[N]; // group IDs } parameters { real intercept; // Population intercept vector[K] beta; // Population slope parameters real<lower=0> sigma; // population standard deviation real u[J]; // random effects real<lower=0> sigma_u; // standard deviation of random effects real<lower=0, upper=1> B; // negative binomial dispersion parameter } transformed parameters { real beta_0j[J]; // varying intercepts real mu[N]; // individual means real A[N]; // linking function (neg_binomial alpha parameter) //Varying intercepts definition for (j in 1:J) { beta_0j[j] <- intercept + u[j]; }
// individual means for (n in 1:N) { mu[n] <- beta_0j[groups[n]] + x[n] * beta; A[n]<-exp(mu[n]) * B; } } model { // Priors beta ~ normal(0,10); B ~ beta(2,2); // Random effects distribution u ~ normal(0,sigma_u); // Likelihood part of Bayesian inference for (n in 1:N) { y[n] ~ neg_binomial(A[n], B); } } """Bob Carpenter
Jan 15, 2016, 1:21:26 PM1/15/16
to stan-...@googlegroups.com
When you say errors, what exactly are you seeing?
It helps if you give us exactly what you typed into R
and exactly what it spit back.
The shape parameter is the first argument, so somehow
A[n] is set to 0 for some n in 1:N. You can use print
statements to track through the code and see what's happening.
I'd also recommend using simulated data to make sure
the model fits when it's well-specified for the data.
- Bob
> On Jan 15, 2016, at 11:09 AM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> So I successfully created my first mixed effects Gaussian model with STAN. It compiled and gave good results. Now I am trying to change the model to model a negative binomial response. The model compiles but fails to converge. I haven't found much about the proper priors for the neg_binomial(alpha, beta) function. But alpha obviously needs to be greater than zero, and beta should be bounded between 0 and 1. The conjugate prior of the negative binomial distribution is the beta distribution is the beta distribution, and this seems to fit those criteria nicely. However, I get the following errors:
> --
> You received this message because you are subscribed to the Google Groups "Stan users mailing list" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to stan-users+...@googlegroups.com.
> To post to this group, send email to stan-...@googlegroups.com.
> For more options, visit https://groups.google.com/d/optout.
It helps if you give us exactly what you typed into R
and exactly what it spit back.
The shape parameter is the first argument, so somehow
A[n] is set to 0 for some n in 1:N. You can use print
statements to track through the code and see what's happening.
I'd also recommend using simulated data to make sure
the model fits when it's well-specified for the data.
- Bob
> On Jan 15, 2016, at 11:09 AM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> So I successfully created my first mixed effects Gaussian model with STAN. It compiled and gave good results. Now I am trying to change the model to model a negative binomial response. The model compiles but fails to converge. I haven't found much about the proper priors for the neg_binomial(alpha, beta) function. But alpha obviously needs to be greater than zero, and beta should be bounded between 0 and 1. The conjugate prior of the negative binomial distribution is the beta distribution is the beta distribution, and this seems to fit those criteria nicely. However, I get the following errors:
> You received this message because you are subscribed to the Google Groups "Stan users mailing list" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to stan-users+...@googlegroups.com.
> To post to this group, send email to stan-...@googlegroups.com.
> For more options, visit https://groups.google.com/d/optout.
Jason Tilley
Jan 15, 2016, 2:10:39 PM1/15/16
to Stan users mailing list
Good advice. I will see if I can make the appropriate modifications and test with simulated data. I guess there is no actual error. I should have called them messages. I am using Python, not R. But using PyStan, after setting the model, I call it as:
The model runs through all the iterations, but when I call print(fit) I get the following error instead of the usual output table:
Once again, I appreciate your help and patience with my gross misunderstanding of advanced models.
model_dat = ({'N':len(df), 'K': 2, 'J': 9, 'y': list(df['Y'].astype(int)), 'x': np.matrix([list(df['X1']), list(pd.Categorical(df['X2']).codes)]).T, 'groups': list(pd.Categorical(df['groups']).codes + 1) // too make it (1:J) })
fit = pystan.stan(model_code=model_code, data=model_dat, chains=4)Traceback (most recent call last): File "<stdin>", line 1, in <module> File "stanfit4anon_model_ce308d62b54c6136648513401f98e15f_2834170169694085174.pyx", line 580, in stanfit4anon_model_ce308d62b54c6136648513401f98e15f_2834170169694085174.StanFit4Model.__repr__ (/var/folders/34/hrtbnddj7fv1ztqqgc3l8rfw0000gn/T/tmpHVJ474/stanfit4anon_model_ce308d62b54c6136648513401f98e15f_2834170169694085174.cpp:11263) File "stanfit4anon_model_ce308d62b54c6136648513401f98e15f_2834170169694085174.pyx", line 576, in stanfit4anon_model_ce308d62b54c6136648513401f98e15f_2834170169694085174.StanFit4Model.__str__ (/var/folders/34/hrtbnddj7fv1ztqqgc3l8rfw0000gn/T/tmpHVJ474/stanfit4anon_model_ce308d62b54c6136648513401f98e15f_2834170169694085174.cpp:11139) File "/opt/local/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/pystan/misc.py", line 81, in _print_stanfit s = _summary(fit, pars, probs) File "/opt/local/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/pystan/misc.py", line 205, in _summary ss = _summary_sim(fit.sim, pars, probs) File "/opt/local/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/pystan/misc.py", line 315, in _summary_sim ess_and_rhat = np.array([pystan.chains.ess_and_splitrhat(sim, n) for n in tidx_colm]) File "/opt/local/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/pystan/chains.py", line 34, in ess_and_splitrhat return (ess(sim, n), splitrhat(sim, n)) File "/opt/local/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/pystan/chains.py", line 13, in ess return _chains.effective_sample_size(sim, n) File "pystan/_chains.pyx", line 128, in pystan._chains.effective_sample_size (pystan/_chains.cpp:2491)AssertionError: nanOnce again, I appreciate your help and patience with my gross misunderstanding of advanced models.
Thanks
Bob Carpenter
Jan 15, 2016, 2:20:21 PM1/15/16
to stan-...@googlegroups.com
This looks like it may be a bug in PyStan. I have
no idea how that works.
I'll repost your message in a new thread so someone
who knows PyStan will see it.
- Bob
no idea how that works.
I'll repost your message in a new thread so someone
who knows PyStan will see it.
- Bob
Bob Carpenter
Jan 15, 2016, 2:21:21 PM1/15/16
to Stan users mailing list
I'm just reposting this message from Jason Tilley with
a more informative subject so someone will see it.
Thanks,
- Bob
Begin forwarded message:
Jason Tilley
Jan 15, 2016, 2:34:50 PM1/15/16
to stan-...@googlegroups.com
Well I might have good news. I still need to validate the model, but I added the following to the code:
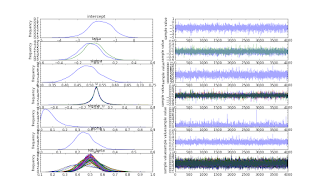
Looking through the chains, I noticed that my population sigma was growing to a ridiculously large number. I added upper=10 for sigma, and the model gives me sensible output now. So I'm very pleased about that. Here is a plot of my results. I need to figure out how to clean it up better. Hopefully you can see the full resolution image. Looking at it, I wonder if I shouldn't constrain sigma even more.
fit = pystan.stan(model_code=model_code, data=model_dat, chains=4), sample_file=home+'/Desktop/model_samp.txt')Looking through the chains, I noticed that my population sigma was growing to a ridiculously large number. I added upper=10 for sigma, and the model gives me sensible output now. So I'm very pleased about that. Here is a plot of my results. I need to figure out how to clean it up better. Hopefully you can see the full resolution image. Looking at it, I wonder if I shouldn't constrain sigma even more.
Bob Carpenter
Jan 15, 2016, 2:46:21 PM1/15/16
to stan-...@googlegroups.com
We recommend only constraining sigma > 0 and adding
a weakly informative prior for it (that doesn't impose
a hard constraint like uniform or bound sigma away from
0 strongly like the gamma priors). The problem with
just adding an arbitrary constraint is that it has
a very strong effect on the prior uncertainty.
- Bob
> On Jan 15, 2016, at 2:34 PM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> Well I might have good news. I still need to validate the model, but I added the following to the code:
>
> fit = pystan.stan(model_code=model_code, data=model_dat, chains=4),
> sample_file=home+'/Desktop/model_samp.txt')
>
> Looking through the chains, I noticed that my population sigma was growing to a ridiculously large number. I added upper=10 for sigma, and the model gives me sensible output now. So I'm very pleased about that. Here is a plot of my results. I need to figure out how to clean it up better. Hopefully you can see the full resolution image Looking at it, I wonder if I shouldn't constrain sigma even more.
a weakly informative prior for it (that doesn't impose
a hard constraint like uniform or bound sigma away from
0 strongly like the gamma priors). The problem with
just adding an arbitrary constraint is that it has
a very strong effect on the prior uncertainty.
- Bob
> On Jan 15, 2016, at 2:34 PM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> Well I might have good news. I still need to validate the model, but I added the following to the code:
>
> fit = pystan.stan(model_code=model_code, data=model_dat, chains=4),
> sample_file=home+'/Desktop/model_samp.txt')
>
Jason Tilley
Jan 15, 2016, 3:08:22 PM1/15/16
to Stan users mailing list
Good to know. So it does seem to be a prior problem at least. Do you mean adding a weekly informative prior for sigma or some other parameter? Would beta ~ normal(0, sigma) help?
Bob Carpenter
Jan 15, 2016, 3:23:25 PM1/15/16
to stan-...@googlegroups.com
Prior for sigma. As in sigma ~ normal(0, 2) or something like that,
depending on the scale of the data for which sigma is the scale
parameter.
- Bob
depending on the scale of the data for which sigma is the scale
parameter.
- Bob
Allen B. Riddell
Jan 15, 2016, 3:32:43 PM1/15/16
to stan-...@googlegroups.com
Hi Jason,
This is fixed in the latest version of PyStan. If you upgrade the error
should disappear.
Best,
Allen
This is fixed in the latest version of PyStan. If you upgrade the error
should disappear.
Best,
Allen
Jason Tilley
Jan 15, 2016, 4:06:20 PM1/15/16
to Stan users mailing list, a...@ariddell.org
I can't thank you enough. Once I get everything here ironed out, I can move on to the final step: making it multivariate! I'll do my best not to abuse the groups generosity.
Andrew Gelman
Jan 15, 2016, 6:56:21 PM1/15/16
to stan-...@googlegroups.com
Just to clarify, sigma ~ normal(0,2) but also with the <lower=0> in the sigma declaration.
Jason Tilley
Jan 15, 2016, 8:38:58 PM1/15/16
to Stan users mailing list, gel...@stat.columbia.edu
Thank you. Yes. This did work for me. I'm not 100% sure my model is correctly specified, but it is certainly a working model. I was shooting for a random intercept model here. Here is the final model code that I used.
model_code = """ data { int<lower=0> N; //rows of data int<lower=0> K; // number of covariates int<lower=0> J; // number of groups matrix[N,K] x; // design matrix (predictors) int y[N]; // response (outcomes) int<lower=1, upper=J> groups[N]; // group IDs } parameters { real intercept; // Population intercept vector[K] beta; // Population slope parameters real<lower=0> sigma; // population standard deviation real u[J]; // random effects real<lower=0> sigma_u; // standard deviation of random effects real<lower=1.0e-20, upper=1> B; // negative binomial beta parameter } transformed parameters { real beta_0j[J]; // varying intercepts real<lower=-100> mu[N]; // individual means real<lower=1.0e-20> A[N]; // negative binomial alpha parameter //Varying intercepts definition for (j in 1:J) { beta_0j[j] <- intercept + u[j]; }
// individual means for (n in 1:N) { mu[n] <- beta_0j[groups[n]] + x[n] * beta; A[n]<-exp(mu[n]) * B; // linking function } } model { // Priors sigma ~ normal(0,2); beta ~ normal(0,10); //B ~ beta(2,2); // Random effects distribution u ~ normal(0,sigma_u); // Data Model for (n in 1:N) { y[n] ~ neg_binomial(A[n], B); } } """Bob Carpenter
Jan 16, 2016, 1:45:23 PM1/16/16
to stan-...@googlegroups.com
You shouldn't need those lower=1e-20 bounds.
Rather than writing a parameter B and a comment that
says it's "beta", just call it beta! Also, why constrain
it to (0,1)?
Adding multiplicative invariances (B * mu)
is problematic in that it makes banana-shaped posteriors.
You can multiply B by 1/c and multiply mu by c and
you get the same product.
And you really want to vectorize, but that's just an
efficiency issue.
- Bob
Rather than writing a parameter B and a comment that
says it's "beta", just call it beta! Also, why constrain
it to (0,1)?
Adding multiplicative invariances (B * mu)
is problematic in that it makes banana-shaped posteriors.
You can multiply B by 1/c and multiply mu by c and
you get the same product.
And you really want to vectorize, but that's just an
efficiency issue.
- Bob
Jason Tilley
Jan 17, 2016, 4:26:14 PM1/17/16
to Stan users mailing list
Well the main reason I chose B was that I needed to differentiate between the NB beta parameter and my slope ("beta") parameters. Perhaps NB_beta would be more informative, or I could rename my slopes to "m". I was under the assumption that in a negative binomial distribution that alpha is constained to be > 0 and the beta parameter is bound to the interval [0,1]. Does the negative binomial function automatically know this? I am working on making the code more computationally efficient (eg., vectorizing) as well as simpler in design (shorter and more readable). However, at the moment, confidence in knowing what the code is doing is more important to me than efficiency. The code is running fast enough for my needs at the moment. Forgive my ignorance, but what is this c parameter you speak of? I would like to try include this final suggestion.
I did remove the two constraints as you suggested. The code did run and provide a solution. Strangely, it is predicting the NB beta as 1.3e10, which I thought must be constrained to [0,1]. Maybe the mu * c trick will help things out.
I still think my basic model structure is not as intended for the model I have in mind. But I think I am slowly sorting that out. I look forward to being more proficient in STAN. I think it will be my goto modeling solution once I have a better understanding of the language and non-Gaussian models in general. Thanks for the help.
Andrew Gelman
Jan 17, 2016, 4:34:06 PM1/17/16
to stan-...@googlegroups.com
If you have a parameter estimated at 1.3e10, you should either rescale something in your model or put in an informative prior, or both.
Jason Tilley
Jan 17, 2016, 5:01:22 PM1/17/16
to Stan users mailing list, gel...@stat.columbia.edu
Wow, I feel honored to be speaking to such a respected group of statisticians. I tried the informative prior route (I think) and set the prior for the NB_beta as NB_beta ~ beta(2,2). Am I close here?
Bob Carpenter
Jan 17, 2016, 5:03:23 PM1/17/16
to stan-...@googlegroups.com
No, the parameter is only restricted to be positive.
If you can write down your density, you should be
able to just code it directly in Stan by working
through the definitions.
- Bob
If you can write down your density, you should be
able to just code it directly in Stan by working
through the definitions.
- Bob
Bob Carpenter
Jan 17, 2016, 5:04:22 PM1/17/16
to stan-...@googlegroups.com
That's still a very weak prior. Plot it to
see.
- Bob
> On Jan 17, 2016, at 5:01 PM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> Wow, I feel honored to be speaking to such a respected group of statisticians. I tried the informative prior route (I think) and set the prior for the NB_beta as NB_beta ~ beta(2,2). Am I close here?
>
see.
- Bob
> On Jan 17, 2016, at 5:01 PM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> Wow, I feel honored to be speaking to such a respected group of statisticians. I tried the informative prior route (I think) and set the prior for the NB_beta as NB_beta ~ beta(2,2). Am I close here?
>
Bob Carpenter
Jan 17, 2016, 5:05:22 PM1/17/16
to stan-...@googlegroups.com
Also, a beta variate is bound in (0,1), so it can't be on the order
of 1e10.
- Bob
> On Jan 17, 2016, at 5:01 PM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> Wow, I feel honored to be speaking to such a respected group of statisticians. I tried the informative prior route (I think) and set the prior for the NB_beta as NB_beta ~ beta(2,2). Am I close here?
>
of 1e10.
- Bob
> On Jan 17, 2016, at 5:01 PM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
>
> Wow, I feel honored to be speaking to such a respected group of statisticians. I tried the informative prior route (I think) and set the prior for the NB_beta as NB_beta ~ beta(2,2). Am I close here?
>
Jason Tilley
Jan 17, 2016, 7:59:16 PM1/17/16
to stan-...@googlegroups.com
I am still a bit confused. Taking some advice from this paper, they mention this (although its hard to tell if I'm taking it in the right context here):
if one assumes Uij ∼ NB(ψ, ηij )... the NB-I distribution is the only appropriate choice for the multivariate negative binomial model and mean parameterizations are often used such that ψ = σ2 and ηij = λij/ψ for j ∈ {0, 1, 2, 3}. The covariates could be incorporated as the usual log-linear model λij = exp(x′ijβj)
So I incorporated the following into my model:
alpha <- sigma * sigma;and
for (n in 1:N) { mu[n] <- beta_0j[groups[n]] + x[n] * beta; lambda[n]<-exp(mu[n]); NB_beta[n]<-lambda[n] / alpha;}model_code = """ data { int<lower=0> N; //rows of data int<lower=0> K; // number of covariates int<lower=0> J; // number of groups matrix[N,K] x; // design matrix (predictors) int y[N]; // response (outcomes) int<lower=1, upper=J> groups[N]; // group IDs } parameters { real intercept; // Population intercept vector[K] beta; // Population slope parameters real<lower=0> sigma; // population standard deviation real u[J]; // random effects real<lower=0> sigma_u; // standard deviation of random effects } transformed parameters { real beta_0j[J]; // varying intercepts real<lower=-100> mu[N]; // individual means real alpha; // negative binomial alpha parameter real NB_beta[N]; // negative binomial beta parameter real lambda[N]; // exp(mu) //real c; // a constant? alpha <- sigma * sigma; //Varying intercepts definition for (j in 1:J) { beta_0j[j] <- intercept + u[j]; }
// individual means for (n in 1:N) { mu[n] <- beta_0j[groups[n]] + x[n] * beta; lambda[n]<-exp(mu[n]); NB_beta[n]<-lambda[n] / alpha; } } model { // Priors sigma ~ normal(0,2); beta ~ normal(0,10); NB_beta ~ beta(2,2); // Random effects distribution u ~ normal(0,sigma_u); // Data Model for (n in 1:N) {Michael Betancourt
Jan 17, 2016, 8:04:54 PM1/17/16
to stan-...@googlegroups.com
Please see the description of the negative binomial implementations in the Stan manual.
There are over 20 different parameterizations of this distribution throughout the statistical
literature, which causes no end of confusion. If you want to use one that we have not
implemented then you’ll have to do all of the transformations yourself.
On Jan 18, 2016, at 12:59 AM, 'Jason Tilley' via Stan users mailing list <stan-...@googlegroups.com> wrote:
I am still a bit confused. Taking some advice from this paper, they mention this (although its hard to tell if I'm taking it in the right context here):if one assumes Uij ∼ NB(ψ, ηij )... the NB-I distribution is the only appropriate choice for the multivariate negative binomial model and mean parameterizations are often used such that ψ = σ2 and ηij = λij/ψ for j ∈ {0, 1, 2, 3}. The covariates could be incorporated as the usual log-linear model λij = exp(x′ijβj)
So I incorporated the following into my model:
for (n in 1:N) {
mu[n] <- beta_0j[groups[n]] + x[n] * beta;
lambda[n]<-exp(mu[n]);
NB_beta[n]<-lambda[n] / alpha;
}
If I do not set a prior for NB_beta, NB_beta is still > 1. If I incorporate NB_beta ~ beta(2,2) then the NB_beta results as [0,1]. You mention that NB_beta ~ beta(2,2) is too weak of a prior. Is there some other way I should specify my priors to me more informative. Or perhaps a reference you could point me to on the subject. I really don't have any relevant data to go by other than my own dataset. The model is now giving Rhats very close to one, but I would like to make sure I set my priors properly (and also provide proper information for anyone using this thread in the future). Here is my code currently.
Jason Tilley
Jan 17, 2016, 8:54:51 PM1/17/16
to stan-...@googlegroups.com
I apologize for the barrage of questions. I understand that modeling is something that can take years or decades to master, and I certainly have a long way to go. I truly do appreciate all the helpful suggestions and will try to implement everybody's advise as much as possible. I was not intending to reinvent the wheel, so any appearance of that probably just shows how far off base I am. I have been spoiled by R and Python, so getting myself from the standard Y ~ X1 + X2 + (1|groups) is not proving easy. I can happily say that I've learned much in just a few short days, and I owe it to STAN and this incredibly talented group. Normally, I could direct these questions to my major professor (very adept in BUGS), but she will be on maternity leave the next few weeks. Honestly, I have already directed my problem to an outside statistics professor that is friends with one of my coauthors. I think it is likely he can provide a solid model in the short time frame we are working with. But this hasn't kept me from wanting to keep learning about the power of STAN. I am a biologist not a statistician, but I expect most problems in my career will require strong modeling abilities to properly answer the questions I explore. I hope all this personal information doesn't strike you as strange, I am just trying to give an explantation for my overuse of this group. Bob has been extremely patient, Gelman has written the best Bayesian modeling book I know of, Allen has opened up a world of modeling in Python for me, and I have thoroughly enjoyed Dr. Betancourt's YouTube lectures. I am very lucky to have advice from all of you, it just may take some time before I can actually understand and implement that advice. I think STAN's greatness is the result of all of your enthusiasm to share knowledge, not only your brilliance. I am amazed that you all can even take the time to help people. I just want to let you all know that I am grateful for your help.
Ben Goodrich
Jan 17, 2016, 9:11:17 PM1/17/16
to Stan users mailing list
On Sunday, January 17, 2016 at 8:54:51 PM UTC-5, Jason Tilley wrote:
I apologize for the barrage of questions. I understand that modeling is something that can take years or decades to master, and I certainly have a long way to go. I truly do appreciate all the helpful suggestions and will try to implement everybody's advise as much as possible. I was not intending to reinvent the wheel, so any appearance of that probably just shows how far off base I am. I have been spoiled by R and Python, so getting myself from the standard Y ~ X1 + X2 + (1|groups) is not proving easy.
If that is the case, perhaps you would be better served starting with the stan_glmer() function in the rstanarm package, which also permits negative binomial models.
Ben
Jason Tilley
Jan 17, 2016, 9:20:19 PM1/17/16
to stan-...@googlegroups.com
Thank you. This might be a good way for me to transition into STAN.
Jason Tilley
Jan 18, 2016, 4:52:16 PM1/18/16
to Stan users mailing list
Would you happen to know how I might expose the STAN code used to fit the model in rstanarm?
Ben Goodrich
Jan 18, 2016, 5:01:39 PM1/18/16
to Stan users mailing list
On Monday, January 18, 2016 at 4:52:16 PM UTC-5, Jason Tilley wrote:
Would you happen to know how I might expose the STAN code used to fit the model in rstanarm?
Jason Tilley
Jan 18, 2016, 5:56:42 PM1/18/16
to Stan users mailing list
thanks!
Jason Tilley
Jan 18, 2016, 9:39:11 PM1/18/16
to Stan users mailing list
I want to take one more stab at this. The STAN code produced by R was more complex than I could handle. So if I was to set the prior for a negative binomial distribution, it seems the conjugate prior for this would be a beta distribution? Would this be the correct prior to use? Considering I have novel data, I still don't understand why setting a flat (non informative?) prior such as uniform(0,1) isn't the right choice. But if I wanted to set a strong prior, for example, could I estimate the α and β parameters of the beta distribution doing something like this with my existing data?
model_code = """ data { int<lower=0> N; //rows of data int y[N]; // response (outcomes) } parameters { real beta; // the lambda parameter of a Poisson distribution also? real alpha; // negative binomial alpha parameter } model { beta ~ uniform(0,1); // Data Model y ~ neg_binomial(alpha, beta); } """From this I got the result:
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhatbeta 0.82 7.5e-3 0.14 0.49 0.75 0.86 0.93 0.99 343.0 1.0alpha 0.34 5.0e-3 0.08 0.2 0.29 0.34 0.39 0.51 251.0 1.01lp__ -77.92 0.04 0.91 -80.24 -78.32 -77.69 -77.29 -76.8 452.0 1.0Then from this, could I use these parameters for my strong prior in my full model. The following is obviously trimmed down from the mixed model I'm working on.
model_code = """ data { int<lower=0> N; //rows of data int y[N]; // response (outcomes) } parameters { real beta; // the lambda parameter of a Poisson distribution also? real alpha; // negative binomial alpha parameter } model { beta ~ beta(0.34,0.82); // Data Model y ~ neg_binomial(alpha, beta); } """Once again, from my limited understanding, it is a bad idea to set a prior from the same data you are modeling. Maybe I am wrong or maybe there are exceptions (e.g. mixed models). Is this where a weakly informative prior would be useful? If so, how would I determine the intermediate distribution between the flat and strong prior that would provide a good compromise?
Andrew Gelman
Jan 18, 2016, 9:42:40 PM1/18/16
to stan-...@googlegroups.com
Hi don’t worry about conjugate prior, just do whatever makes sense in context of model. Once you’ve fit your model, you can simulate fake data from the model (as discussed in chapter 6 of BDA) and check that the simulated data look like the real data. This is called posterior predictive checking and it is an important part of building trust in whatever model you fit.
A
Jason Tilley
Jan 18, 2016, 10:05:53 PM1/18/16
to Stan users mailing list, gel...@stat.columbia.edu
Thanks! I'm on Chapter 3 right now. I'll give that a look.
Bob Carpenter
Jan 19, 2016, 3:56:26 PM1/19/16
to stan-...@googlegroups.com
You'd use a hierarchical/multilevel model if you wanted
to do that --- no need to do what you're doing. See
the Gelman and Hill book on regression --- it's awesome.
Or check out Andrew's paper on "how many Xs" for specifically
negative binomial examples:
http://www.stat.columbia.edu/~gelman/research/published/overdisp_final.pdf
- Bob
to do that --- no need to do what you're doing. See
the Gelman and Hill book on regression --- it's awesome.
Or check out Andrew's paper on "how many Xs" for specifically
negative binomial examples:
http://www.stat.columbia.edu/~gelman/research/published/overdisp_final.pdf
- Bob
Jason Tilley
Jan 19, 2016, 4:47:21 PM1/19/16
to stan-...@googlegroups.com
I will have to check out that book. I really don't understand how Dr. Gelman finds the time. Your timing is great. I was just trying to make sense of the negative binomial prior thing, and the fact that you asked why would I constrain β to be [0,1]. Well my thoughts were that with NB(r,p), the probability p can't be higher than 1 right? That was what tripped me up on this. I didn't realize that Dr. Gelman had his own pmf of NB. So I started playing, and now I realize why you asked me that. This is what I did in Python to test it:
import numpy as npfrom scipy.special import binom
def Gelman_NB(theta, alpha, beta): term1 = binom((theta + alpha - 1),(alpha - 1)) term2 = (beta / (beta + 1)) ** alpha term3 = (1 / (beta + 1)) ** theta x = term1 * term2 * term3 return x
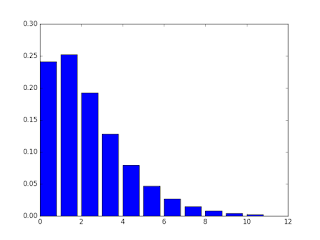
theta = np.arange(0,11,1)pmf = Gelman_NB(theta, 2.2, 1.1)plt.bar(theta, pmf)plt.show()
print(pmf.sum()) # should intergrate to one for theta = [0, inf]And sure enough, I could have β be greater than 1, and the sum in this range was close to 1. So I guess this makes me one step closer to understanding the proper prior for the NB. Its very useful that α / β = the mean as well. This is my pmf plot. Hopefully, I made the function right.
Jason
Reply all
Reply to author
Forward
0 new messages