Confusion about what happens with R-hat in a long-tailed distribution
114 views
Skip to first unread message
Andrew Gelman
Apr 11, 2014, 6:10:00 AM4/11/14
to stan...@googlegroups.com
Hi all. As we’ve been discussing, R-hat could fail in settings such as a Cauchy distribution because it is based on means and variances which are unstable. There are two issues here: First, with a long-tailed distribution, any statistics based on means and variances will be so noisy as to be useless. Second, we can have a situation where the MCMC really does converge but we can’t notice it because R-hat is crap.
But I’m actually confused what is going on here. The source of my confusion is that I decided to run the model on a Cauchy example to see how it worked. I tried it two ways: (1) cauchy_1.stan programs the Cauchy directly, so Stan (using the current Euclidean Nuts algorithm) will not fully explore the space; (2) cauchy_2.stan programs the Cauchy as the ratio of two independent normals. So Stan will work just fine and essentially move around the space at random:
cauchy_1.stan:
parameters {
real theta;
}
model {
theta ~ student_t(1,0,1);
}
cauchy_2.stan:
parameters {
real theta_1;
real theta_2;
}
transformed parameters {
real theta;
theta <- theta_1/theta_2;
}
model {
theta_1 ~ normal(0,1);
theta_2 ~ normal(0,1);
}
Then I ran in R for 10,000 iterations. I was surprised by the results. The first surprising thing was that cauchy_1 wasn’t so bad! It had some problems exploring the extremes but it did reasonably well (if not perfect) on its 95% intervals. The second surprise was that R-hat was stable for both models. I was expecting a noisy meaningless R-hat in both cases because of the whole variance issue. But it did not happen. I suspect that what’s going on is that, yes, means and variances for Cauchy are noisy (and, indeed, the posterior mean, se_mean, and sd of theta are meaningless for both models), but that because R-hat is a _ratio_, the worst behavior ends up canceling in the numerator and denominator.
Here are the results of the 10,000-iteration Stan runs. Running it repeatedly gives similar results:
Inference for Stan model: cauchy_1.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta 0.2 0.4 19.4 -12.2 -0.9 0.0 0.9 11.9 2594 1
lp__ -1.3 0.1 1.8 -6.5 -1.8 -0.6 -0.1 0.0 1038 1
Inference for Stan model: cauchy_2.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta_1 0.0 0.0 1.0 -2.0 -0.7 0.0 0.7 1.9 11428 1
theta_2 0.0 0.0 1.0 -1.9 -0.7 0.0 0.7 1.9 12013 1
theta 15.1 15.3 1532.6 -12.3 -1.0 0.0 1.0 13.5 10005 1
lp__ -1.0 0.0 1.0 -3.5 -1.4 -0.7 -0.3 0.0 5637 1
Model cauchy_2 is in some sense a pure illustration of the issue because we have a long-tailed distribution in theta, but the parameterization is set up so that convergence is essentially immediate.
But I’m actually confused what is going on here. The source of my confusion is that I decided to run the model on a Cauchy example to see how it worked. I tried it two ways: (1) cauchy_1.stan programs the Cauchy directly, so Stan (using the current Euclidean Nuts algorithm) will not fully explore the space; (2) cauchy_2.stan programs the Cauchy as the ratio of two independent normals. So Stan will work just fine and essentially move around the space at random:
cauchy_1.stan:
parameters {
real theta;
}
model {
theta ~ student_t(1,0,1);
}
cauchy_2.stan:
parameters {
real theta_1;
real theta_2;
}
transformed parameters {
real theta;
theta <- theta_1/theta_2;
}
model {
theta_1 ~ normal(0,1);
theta_2 ~ normal(0,1);
}
Then I ran in R for 10,000 iterations. I was surprised by the results. The first surprising thing was that cauchy_1 wasn’t so bad! It had some problems exploring the extremes but it did reasonably well (if not perfect) on its 95% intervals. The second surprise was that R-hat was stable for both models. I was expecting a noisy meaningless R-hat in both cases because of the whole variance issue. But it did not happen. I suspect that what’s going on is that, yes, means and variances for Cauchy are noisy (and, indeed, the posterior mean, se_mean, and sd of theta are meaningless for both models), but that because R-hat is a _ratio_, the worst behavior ends up canceling in the numerator and denominator.
Here are the results of the 10,000-iteration Stan runs. Running it repeatedly gives similar results:
Inference for Stan model: cauchy_1.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta 0.2 0.4 19.4 -12.2 -0.9 0.0 0.9 11.9 2594 1
lp__ -1.3 0.1 1.8 -6.5 -1.8 -0.6 -0.1 0.0 1038 1
Inference for Stan model: cauchy_2.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta_1 0.0 0.0 1.0 -2.0 -0.7 0.0 0.7 1.9 11428 1
theta_2 0.0 0.0 1.0 -1.9 -0.7 0.0 0.7 1.9 12013 1
theta 15.1 15.3 1532.6 -12.3 -1.0 0.0 1.0 13.5 10005 1
lp__ -1.0 0.0 1.0 -3.5 -1.4 -0.7 -0.3 0.0 5637 1
Model cauchy_2 is in some sense a pure illustration of the issue because we have a long-tailed distribution in theta, but the parameterization is set up so that convergence is essentially immediate.
Michael Betancourt
Apr 11, 2014, 6:25:28 AM4/11/14
to stan...@googlegroups.com
The manifestation of a Cauchy having no mean is that the variance of the Monte Carlo estimator
for the mean is constant and does not decrease with ESS. If you look at traces you’ll see the
estimate for the mean drift around within that variance, but the estimate does not diverge and
should should track around the median.
I think your intuition is right — when you compute Rhat you’re looking at the ratio of two variances
that are seemingly well-behaved but don’t decrease with increasing ESS. That would mean that
Rhat looks fine but it won’t be particularly sensitive to convergence (it should be a pretty conservative
test).
> --
> You received this message because you are subscribed to the Google Groups "stan development mailing list" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to stan-dev+u...@googlegroups.com.
> For more options, visit https://groups.google.com/d/optout.
for the mean is constant and does not decrease with ESS. If you look at traces you’ll see the
estimate for the mean drift around within that variance, but the estimate does not diverge and
should should track around the median.
I think your intuition is right — when you compute Rhat you’re looking at the ratio of two variances
that are seemingly well-behaved but don’t decrease with increasing ESS. That would mean that
Rhat looks fine but it won’t be particularly sensitive to convergence (it should be a pretty conservative
test).
> You received this message because you are subscribed to the Google Groups "stan development mailing list" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to stan-dev+u...@googlegroups.com.
> For more options, visit https://groups.google.com/d/optout.
Ben Goodrich
Apr 11, 2014, 12:39:51 PM4/11/14
to stan...@googlegroups.com, gel...@stat.columbia.edu
On Friday, April 11, 2014 6:10:00 AM UTC-4, Andrew Gelman wrote:
Hi all. As we’ve been discussing, R-hat could fail in settings such as a Cauchy distribution because it is based on means and variances which are unstable. There are two issues here: First, with a long-tailed distribution, any statistics based on means and variances will be so noisy as to be useless. Second, we can have a situation where the MCMC really does converge but we can’t notice it because R-hat is crap.
I foisted a third situation on my QMSS class a couple of weeks ago, where the chains didn't converge but the R-hat statistics weren't that bad (depending on the seed). The attached .stan file has no data but draws from the prior predictive distribution of standardized coefficients that is implied by an LKJ prior on the correlation matrix among the predictors and outcome. Except it is deliberately inefficient because it has a discontinuity in the parameter space due to a complicated multivariate inequality constraint on beta_check:
Anyway, if you do something like
you may (again depending on the seed) get something like
temp <- dot_self(beta_check * L);
if(temp <= 1) increment_log_prob( (eta - 1) * log1m(temp) );
else increment_log_prob( negative_infinity() );
Anyway, if you do something like
fit <- stan("onion.stan", chains = 0)
fit <- stan(fit = fit, iter = 20000, init_r = 0.5, data = list(eta = 1, K = 5))
print(fit, digits = 2)
you may (again depending on the seed) get something like
Inference for Stan model: onion.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
l[1] -0.01 0.05 0.99 -1.87 -0.69 -0.02 0.65 1.97 356 1.02
l[2] 0.04 0.04 0.99 -1.90 -0.64 0.05 0.70 2.02 541 1.01
l[3] -0.02 0.04 0.95 -1.86 -0.68 -0.04 0.61 1.86 620 1.00
l[4] -0.04 0.04 0.95 -1.88 -0.70 -0.03 0.61 1.80 613 1.01
l[5] -0.04 0.05 0.99 -1.93 -0.72 -0.06 0.64 1.92 403 1.01
l[6] -0.07 0.05 1.02 -2.00 -0.76 -0.10 0.61 1.97 346 1.02
l[7] 0.02 0.05 1.01 -2.06 -0.65 0.03 0.71 1.96 441 1.00
l[8] 0.01 0.05 0.97 -1.89 -0.62 -0.01 0.64 1.97 364 1.01
l[9] 0.10 0.04 0.97 -1.74 -0.57 0.08 0.78 1.99 537 1.00
R2[1] 0.50 0.01 0.19 0.15 0.36 0.49 0.63 0.86 603 1.00
R2[2] 0.29 0.01 0.21 0.01 0.12 0.25 0.43 0.76 545 1.01
R2[3] 0.43 0.01 0.22 0.05 0.25 0.41 0.59 0.85 417 1.01
R2[4] 0.57 0.01 0.23 0.13 0.40 0.59 0.76 0.94 388 1.01
beta_check[1] 0.01 0.04 0.68 -1.26 -0.46 0.00 0.46 1.38 265 1.01
beta_check[2] 0.08 0.05 0.66 -1.19 -0.36 0.07 0.50 1.46 209 1.02
beta_check[3] -0.02 0.04 0.69 -1.42 -0.46 0.00 0.44 1.28 259 1.01
beta_check[4] -0.05 0.04 0.62 -1.31 -0.48 -0.05 0.39 1.08 231 1.02
beta_check[5] 0.07 0.04 0.67 -1.20 -0.38 0.05 0.50 1.40 306 1.00
lp__ -18.60 0.09 2.64 -24.73 -20.18 -18.22 -16.70 -14.49 816 1.00
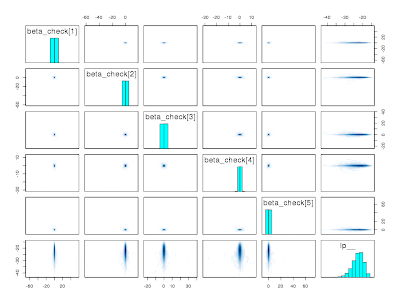
which no one would be too alarmed about. But it didn't actually converge, which is apparent from asymmetry in the pairs plots (again, lower triangle has the first 2 chains, upper triangle as the last 2 chains)
pairs(fit, pars = c("beta_check", "lp__"))
The reason is that the marginal distribution of each element of beta_check has long tails (the mean and variance exist in this situation, but not the skewness) and NUTS can't explore the tails efficiently when you put a discontinuity into the parameter space that tends to bind on the proposed parameters when the Markov chain is currently in the tails. You get high levels of dependence even for 30+ lags
and you reject the null hypothesis that all the chains have converged to the same distribution.
> convergence(fit, R = 200, thin = 40)
[1] "Multivariate loss = 1.001"
disco(x = mat, factors = chain_id, distance = FALSE, R = R)
Distance Components: index 1.00
Source Df Sum Dist Mean Dist F-ratio p-value
factors 3 14.94633 4.98211 1.731 0.0049751
Within 996 2867.41348 2.87893
Total 999 2882.35981
But, I think no one besides me would notice that because they don't look at the pairs plot, the dependence plot, or the distance components test.
If you reparameterize the prior to use a Matt trick instead of an inequality constraint (see onion2.stan), then NUTS samples almost perfectly (the dependence dissipates after 3 lags), you fail to reject the null hypothesis that all the chains have converged to the same distribution,
> convergence(fit, R = 200, thin = 4)
[1] "Multivariate loss = 1"
disco(x = mat, factors = chain_id, distance = FALSE, R = R)
Distance Components: index 1.00
Source Df Sum Dist Mean Dist F-ratio p-value
factors 3 13.42599 4.47533 1.248 0.079602
Within 9996 35831.61495 3.58460
Total 9999 35845.04094and the pairs plots show the concentration at the origin with the occasional trip way into the tails (you never get out to +/- 50 in the first parameterization).
So, the first is certainly a contrived example, but one where the chain means are similar, the means and variances exist, and the R-hats are fine. But the distribution is sufficiently far from Gaussian and the parameterization is sufficiently far from optimal that it doesn't actually converge. And you can see that pretty easily if you look in the right places, but there are a lot of BDA readers who wouldn't look.
Ben
Ben Goodrich
Apr 11, 2014, 12:46:57 PM4/11/14
to stan...@googlegroups.com, gel...@stat.columbia.edu
On Friday, April 11, 2014 12:39:51 PM UTC-4, Ben Goodrich wrote:
On Friday, April 11, 2014 6:10:00 AM UTC-4, Andrew Gelman wrote:Hi all. As we’ve been discussing, R-hat could fail in settings such as a Cauchy distribution because it is based on means and variances which are unstable. There are two issues here: First, with a long-tailed distribution, any statistics based on means and variances will be so noisy as to be useless. Second, we can have a situation where the MCMC really does converge but we can’t notice it because R-hat is crap.I foisted a third situation on my QMSS class a couple of weeks ago, where the chains didn't converge but the R-hat statistics weren't that bad (depending on the seed). The attached .stan file has no data but draws from the prior predictive distribution of standardized coefficients that is implied by an LKJ prior on the correlation matrix among the predictors and outcome.
Forgot attachments.
Ben
Ben Goodrich
Apr 11, 2014, 5:34:25 PM4/11/14
to stan...@googlegroups.com, gel...@stat.columbia.edu
On Friday, April 11, 2014 6:10:00 AM UTC-4, Andrew Gelman wrote:
Then I ran in R for 10,000 iterations. I was surprised by the results. The first surprising thing was that cauchy_1 wasn’t so bad! It had some problems exploring the extremes but it did reasonably well (if not perfect) on its 95% intervals. The second surprise was that R-hat was stable for both models. I was expecting a noisy meaningless R-hat in both cases because of the whole variance issue. But it did not happen. I suspect that what’s going on is that, yes, means and variances for Cauchy are noisy (and, indeed, the posterior mean, se_mean, and sd of theta are meaningless for both models), but that because R-hat is a _ratio_, the worst behavior ends up canceling in the numerator and denominator.
This claim partly depends on the way Stan calculates the Rhat (see below). Putting aside the issue of splitting the chains (which shouldn't be relevant in this case), Stan doesn't do a degrees of freedom adjustment while coda does. With coda's degrees of freedom adjustment, the Rhat is pretty bad (1.2) for plain Cauchy sampling and decent (1.07) for ratio-of-normals Cauchy sampling. So, what is the argument for Stan not doing coda's degrees of freedom adjustment?
Ben
library(rstan)
library(coda)
library(parallel)
cauchy <-
'
parameters {
real theta;
}
model {
theta ~ cauchy(0,1);
}
'
fit <- stan(model_code = cauchy, chains = 0)
fit <- sflist2stanfit(mclapply(1:16, mc.cores = detectCores(), FUN = function(i) {
stan(fit = fit, chains = 1, seed = 12345, chain_id = i, refresh = 0, iter = 10000)
}))
print(fit, digits = 2)
# Inference for Stan model: cauchy.
# 16 chains, each with iter=10000; warmup=5000; thin=1;
# post-warmup draws per chain=5000, total post-warmup draws=80000.
#
# mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
# theta 0.46 0.73 47.97 -10.40 -0.94 -0.01 0.93 10.87 4322 1
# lp__ -1.28 0.03 1.70 -6.19 -1.75 -0.63 -0.15 0.00 4047 1
gelman.diag(rstan:::as.mcmc.list(fit), multivariate = FALSE)
# Potential scale reduction factors:
#
# Point est. Upper C.I.
# theta 1.2 1.22
# lp__ 1.0 1.01
normal_ratio <-
'
parameters {
real theta[2];
}
model {
theta ~ normal(0,1);
}
generated quantities {
real ratio;
ratio <- theta[1] / theta[2];
}
'
fit2 <- stan(model_code = normal_ratio, chains = 0)
fit2 <- sflist2stanfit(mclapply(1:16, mc.cores = detectCores(), FUN = function(i) {
stan(fit = fit2, chains = 1, seed = 12345, chain_id = i, refresh = 0, iter = 10000)
}))
print(fit2, digits = 2)
# Inference for Stan model: normal_ratio.
# 16 chains, each with iter=10000; warmup=5000; thin=1;
# post-warmup draws per chain=5000, total post-warmup draws=80000.
#
# mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
# theta[1] 0.00 0.00 1.00 -1.95 -0.67 0.00 0.68 1.94 47707 1
# theta[2] 0.00 0.00 1.00 -1.96 -0.67 0.00 0.68 1.96 49254 1
# ratio -0.88 0.76 208.78 -12.84 -1.00 0.00 1.00 12.34 76002 1
# lp__ -1.00 0.01 0.99 -3.69 -1.38 -0.69 -0.29 -0.03 25426 1
gelman.diag(rstan:::as.mcmc.list(fit2), multivariate = FALSE)
# Potential scale reduction factors:
#
# Point est. Upper C.I.
# theta[1] 1.00 1.00
# theta[2] 1.00 1.00
# ratio 1.07 1.07
# lp__ 1.00 1.00
Bob Carpenter
Apr 12, 2014, 7:23:12 AM4/12/14
to stan...@googlegroups.com
Nice analysis! It looks like we should be promoting your
techniques to monitor convergence. Pairs I think we can suggest
using in R and probably in Python --- I don't see how we could
do it from the command line without plugging in some kind of
graphical tool (gnuplot, anyone?).
Is there a description somewhere of what disco() and convergence() do
and how we're supposed to interpret the output?
- Bob
> convergence(fit, R = 200, thin = 40)
[1] "Multivariate loss = 1.001"
disco(x = mat, factors = chain_id, distance = FALSE, R = R)
Distance Components: index 1.00
Source Df Sum Dist Mean Dist F-ratio p-value
factors 3 14.94633 4.98211 1.731 0.0049751
Within 996 2867.41348 2.87893
Total 999 2882.35981
techniques to monitor convergence. Pairs I think we can suggest
using in R and probably in Python --- I don't see how we could
do it from the command line without plugging in some kind of
graphical tool (gnuplot, anyone?).
Is there a description somewhere of what disco() and convergence() do
and how we're supposed to interpret the output?
- Bob
> convergence(fit, R = 200, thin = 40)
[1] "Multivariate loss = 1.001"
disco(x = mat, factors = chain_id, distance = FALSE, R = R)
Distance Components: index 1.00
Source Df Sum Dist Mean Dist F-ratio p-value
factors 3 14.94633 4.98211 1.731 0.0049751
Within 996 2867.41348 2.87893
Total 999 2882.35981
Ben Goodrich
Apr 12, 2014, 9:25:12 AM4/12/14
to stan...@googlegroups.com
Mike still has some objection to including these functions that I am not grasping. All that output is "like" that for ANOVA, except the p-value is not based on the F distribution. Rather it is the proportion of simulations where are more extreme test statistic was observed under random permutations of the output that scramble the chains-time structure. Also, if the index is less than 2 (it is 1 by default), the null hypothesis is that all the chains have the same distribution rather than only the same mean(s). The paper is
https://projecteuclid.org/euclid.aoas/1280842151
That wrapper function is like 15 lines and basically just calls disco() appropriately, which is documented in the energy package.
Ben
https://projecteuclid.org/euclid.aoas/1280842151
That wrapper function is like 15 lines and basically just calls disco() appropriately, which is documented in the energy package.
library(energy)
convergence <- function(object, R = 0, thin = 1, ...) {
mat <- as.matrix(object)
mat <- mat[1:nrow(mat) %% thin == 0,]
chains <- if(is.list(object)) length(object) else ncol(object)
n <- nrow(mat) / chains
chain_id <- rep(1:chains, each = n)
test <- disco(mat, factors = chain_id, distance = FALSE, R = R, ...)
W <- test$within / test$Df.e
B <- test$between / (chains - 1)
names(B) <- NULL
total <- (n - 1) / n * W + B / n
loss <- sqrt(total / W)
test$loss <- loss
print(paste("Multivariate loss =", round(loss, 3)))
return(test)
}
Ben
Andrew Gelman
Apr 12, 2014, 2:31:11 PM4/12/14
to Ben Goodrich, stan...@googlegroups.com
B
What is the degrees of freedom adjustment you speak of?
A
P.S. I think with ratio-of-normals Cauchy sampling, convergence will essentially be immediate. So R-hat “should” really be 1.0 in that case. But, as noted, it’s hard for me to know what R-hat should be doing in the case of an infinite variance, as the usual theory does not apply in that case. As I said in my earlier email, I think that R-hat is working better than it has any right to do, because the ratio is saving its butt.
On Apr 11, 2014, at 11:34 PM, Ben Goodrich <goodri...@gmail.com> wrote:
Ben Goodrich
Apr 12, 2014, 2:42:59 PM4/12/14
to stan...@googlegroups.com, gel...@stat.columbia.edu
It is explained in the details section help(gelman.diag, package = coda) within R or
http://hosho.ees.hokudai.ac.jp/~kubo/Rdoc/library/coda/html/gelman.diag.html
With the ratio-of-normals approach, the Cauchy random variable doesn't enter the log-posterior, so it should definitely converge quickly to the uncorrelated bivariate normal distribution and any convergence indicator for the numerator and denominator should be fine. It is sort of unclear what the Rhat for the ratio in generated quantities "should" be. Since
R = sqrt( [(n - 1) / n * W + 1 / n * B] / W ) = sqrt( (n-1) / n + 1 / n * B / W )
if {B_n / W_n} were bounded as n went to infinity, then R would converge to 1. But I don't think it could be interpreted as a potential scale factor reduction, so it is hard to say what would be a good or bad value of R in this situation.
Ben
http://hosho.ees.hokudai.ac.jp/~kubo/Rdoc/library/coda/html/gelman.diag.html
With the ratio-of-normals approach, the Cauchy random variable doesn't enter the log-posterior, so it should definitely converge quickly to the uncorrelated bivariate normal distribution and any convergence indicator for the numerator and denominator should be fine. It is sort of unclear what the Rhat for the ratio in generated quantities "should" be. Since
R = sqrt( [(n - 1) / n * W + 1 / n * B] / W ) = sqrt( (n-1) / n + 1 / n * B / W )
if {B_n / W_n} were bounded as n went to infinity, then R would converge to 1. But I don't think it could be interpreted as a potential scale factor reduction, so it is hard to say what would be a good or bad value of R in this situation.
Ben
Andrew Gelman
Apr 12, 2014, 3:00:48 PM4/12/14
to Ben Goodrich, stan...@googlegroups.com
Aahh, yes, _that_ degrees-of-freedom correction. The one from my 1992 paper. I removed it from R-hat awhile ago because it just seemed like more trouble than it was worth to always go on explaining it.
Regarding ratio of normals, the point is that we will have essentially instantaneous convergence (because, as you say, the Cauchy doesn’t enter the log posterior), but the posterior for theta (= theta_1/theta_2) really _is_ Cauchy, which means that R-hat for theta really is doing something kinda weird because it is based on estimating a variance that doesn’t exist. The fact that it works at all suggests to me that there’s something that’s cancelling out in the ratio that is R-hat.
A
Ben Goodrich
Apr 12, 2014, 3:10:32 PM4/12/14
to Andrew Gelman, stan...@googlegroups.com
It does seem plausible that B / W is bounded, in which case Stan's Rhat converges to 1. But if you do the dof adjustment, then Rhat converges to the square root of (d+3)/(d+1). Coda does not estimate d to be 1 in this case, which may be reasonable since neither the numerator nor the denominator of d exist either.
Ben
Michael Betancourt
Apr 12, 2014, 6:45:03 PM4/12/14
to stan...@googlegroups.com
>
> P.S. I think with ratio-of-normals Cauchy sampling, convergence will essentially be immediate. So R-hat “should” really be 1.0 in that case. But, as noted, it’s hard for me to know what R-hat should be doing in the case of an infinite variance, as the usual theory does not apply in that case. As I said in my earlier email, I think that R-hat is working better than it has any right to do, because the ratio is saving its butt.
Even though the mean and variance don’t exist, the distribution of the MCMC estimator for the mean is well-defined
> P.S. I think with ratio-of-normals Cauchy sampling, convergence will essentially be immediate. So R-hat “should” really be 1.0 in that case. But, as noted, it’s hard for me to know what R-hat should be doing in the case of an infinite variance, as the usual theory does not apply in that case. As I said in my earlier email, I think that R-hat is working better than it has any right to do, because the ratio is saving its butt.
and has a well-defined mean and variance. The pathology manifests in the estimator variance NOT decreasing
with increasing ESS. This jives with what Andrew sees — because the sample variance does not decrease Rhat
will stabilize almost immediately.
Michael Betancourt
Apr 12, 2014, 7:04:01 PM4/12/14
to stan...@googlegroups.com
The problem is in the sparsity of theory regarding multivariate estimators from Markov chains.
Rhat works because assuming that the Markov chain has converged a univariate MCMC estimator
convergences to a gaussian distribution and the distribution of subsamples/different chains converges
to an F distribution.
But here you’re trying to do look at multivariate estimators, and there is no theory that we’ve been
able to find that discusses the distribution to which these estimators converge. It’s probably going
to be gaussian, but will it be diagonal or will there be correlations? Obviously these details will
be important to establishing a single number that attempts to quantify convergence.
The paper claims a non parametric test via permutations, but there are two concerns. Firstly,
permutation tests have a reputation for horrible type II errors making them weak tests in general
and, secondly, the significance test is trickier here. If the chain hasn’t converged then you’re
not comparing samples from two different distributions but rather samples from an evolving
distribution and it’s not clear how robust permutations are to this difference.
If you want to turn this into a visual diagnostic that indicates a possible lack of convergence
then I have no objection — my objection is in defining a new statistic in which one can claim
“convergence” as we currently treat Rhat.
Ben Goodrich
Apr 12, 2014, 8:19:20 PM4/12/14
to stan...@googlegroups.com
On Saturday, April 12, 2014 7:04:01 PM UTC-4, Michael Betancourt wrote:
The problem is in the sparsity of theory regarding multivariate estimators from Markov chains.Rhat works because assuming that the Markov chain has converged a univariate MCMC estimatorconvergences to a gaussian distribution and the distribution of subsamples/different chains convergesto an F distribution.
I'm with you there.
But here you’re trying to do look at multivariate estimators, and there is no theory that we’ve beenable to find that discusses the distribution to which these estimators converge. It’s probably goingto be gaussian, but will it be diagonal or will there be correlations? Obviously these details willbe important to establishing a single number that attempts to quantify convergence.
But we are already assuming the each Markov chain has a unique stationary distribution without specifying what that distribution is. So, for a test of a null hypothesis that the chains all have the same distribution vs. the alternative hypothesis that at least one chain has a different distribution, I'm not sure we need to know what is the distribution of the scalar function being produced here. I mean even the authors don't try to derive it for their intended use case --- which is whether multiple samples of grouped data come from the same distribution --- instead doing the permutations to get the p-value.
The paper claims a non parametric test via permutations, but there are two concerns. Firstly,permutation tests have a reputation for horrible type II errors making them weak tests in generaland, secondly, the significance test is trickier here. If the chain hasn’t converged then you’renot comparing samples from two different distributions but rather samples from an evolvingdistribution and it’s not clear how robust permutations are to this difference.
I agree that power is (always) something to be concerned about, and I haven't done any rigorous sets of simulations here. But even if the power is middling, I don't think that invalidates the test. My experience (from the BUGS models, the example I posted in response to Andrew, etc.) has been more in the other direction where I see a low p-value and then look more carefully at decide that some chain(s) hadn't converged. But in section 6 of the paper, they show it has credible power in a data context with 30 observations per group. And in theorem 3, they show it is consistent against all alternatives with finite second moments. So, that is an important countervailing point as compared to the Rhat which is only sensitive to mean differences.
So, while I agree that we should look into the power more, one reason why I haven't done more of that already is because I thought Andrew's objection would be the opposite, that the null hypothesis would almost always be rejected because people almost always stop the chains before they technically converge but after the differences have become substantively negligible. That is maybe a valid description of people's experience with BUGS or Gibbs samplers generally, but Stan seems to do a lot better in this regard and you certainly can find examples where you fail to reject the null hypothesis.
If you want to turn this into a visual diagnostic that indicates a possible lack of convergencethen I have no objection — my objection is in defining a new statistic in which one can claim“convergence” as we currently treat Rhat.
But I think we currently claim convergence via the Rhat inappropriately, when we only can claim a lack of mean difference and even then only if all the marginal Rhat statistics are small. For complicated models with many parameters, deciding whether "all" the marginal Rhats are small is a non-trivial task.
Put another way, it is a generalization of what we do with Rhat. If you don't thin afterwards, set the index equal to 2, and run the distance components test marginally, then you have an ANOVA test statistic. And if instead of looking at the p-value, you can look at the loss function, R = sqrt( [(n - 1) / n * W + 1 / n * B] / W ). Or you could do it jointly and I think you have something conceptually the same (not sure about numerically) as the multivariate Brooks-Gelman-Rubin loss function that coda reports and Stan doesn't. Or you can set the index to some number less than 2, thin so that the remaining draws are approximately independent, and test a null hypothesis of convergence to the same distribution. I am not absolutely sure that the test statistic when the index is less than 2 is at least as sensitive to mean differences as when the index is 2, but that seems like a reasonable proposition to investigate.
Ben
Ben Goodrich
Apr 12, 2014, 8:39:13 PM4/12/14
to stan...@googlegroups.com, gel...@stat.columbia.edu
On Friday, April 11, 2014 5:34:25 PM UTC-4, Ben Goodrich wrote:
I forgot to say that the more troubling thing about these ratio-of-normals results
I forgot to say that the more troubling thing about these ratio-of-normals results
fit2 <- sflist2stanfit(mclapply(1:16, mc.cores = detectCores(), FUN = function(i) {
stan(fit = fit2, chains = 1, seed = 12345, chain_id = i, refresh = 0, iter = 10000)
}))
print(fit2, digits = 2)
# Inference for Stan model: normal_ratio.
# 16 chains, each with iter=10000; warmup=5000; thin=1;
# post-warmup draws per chain=5000, total post-warmup draws=80000.
#
# mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
# theta[1] 0.00 0.00 1.00 -1.95 -0.67 0.00 0.68 1.94 47707 1
# theta[2] 0.00 0.00 1.00 -1.96 -0.67 0.00 0.68 1.96 49254 1
# ratio -0.88 0.76 208.78 -12.84 -1.00 0.00 1.00 12.34 76002 1
# lp__ -1.00 0.01 0.99 -3.69 -1.38 -0.69 -0.29 -0.03 25426 1
is that the n_eff for the ratio is much larger than the n_eff for either the numerator or the denominator. That seems untenable even if the Rhat (without the degrees of freedom correction) is legitimately close to 1.
Ben
Andrew Gelman
Apr 13, 2014, 10:02:29 AM4/13/14
to Ben Goodrich, stan...@googlegroups.com
n_eff is based on R-hat, and since R-hat doesn’t really make sense in the case of an infinite variance, I can believe that n_eff doesn’t make sense there either!
Ben Goodrich
Apr 15, 2014, 9:10:45 AM4/15/14
to stan...@googlegroups.com
On Saturday, April 12, 2014 7:04:01 PM UTC-4, Michael Betancourt wrote:
The paper claims a non parametric test via permutations, but there are two concerns. Firstly,permutation tests have a reputation for horrible type II errors making them weak tests in generaland, secondly, the significance test is trickier here. If the chain hasn’t converged then you’renot comparing samples from two different distributions but rather samples from an evolvingdistribution and it’s not clear how robust permutations are to this difference.
It is conceivable that the chains have not converged yet but have taken a similar path toward the stationary distribution, in which case the test may fail to reject the null hypothesis that the chains all have the same distribution, which is not what we want. For a large number of chains with overdispersed chains, this seems unlikely, but I added an option that defaults to TRUE to split the chains like we do with Rhat now.
library(energy)
convergence <- function(object, thin = NA_integer_, R = 0,
split = TRUE, ...) {
if(!isTRUE(thin > 0)) stop("'thin' must be a positive integer")
mat <- as.matrix(object)
if( (nrow(mat) %% thin) != 0 ) {
stop("'thin' value leaves a remainder")
}
mat <- mat[ (1:nrow(mat)) %% thin == 0,,drop=FALSE]
chains <- ifelse(is.list(object), length(object), ncol(object))
if(split) chains <- chains * 2
n <- nrow(mat) / chains
chain_id <- rep(1:chains, each = n)
test <- disco(mat, factors = chain_id,
distance = FALSE, R = R, ...)
W <- test$within / test$Df.e
B <- test$between / (chains - 1)
names(B) <- NULL
total <- (n - 1) / n * W + B / n
loss <- sqrt(total / W)
test$loss <- loss
print(paste("Multivariate loss =", round(loss, 3)))
return(test)
}
[1] "Multivariate loss = 1"
disco(x = mat, factors = chain_id, distance = FALSE, R = R)
Distance Components: index 1.00
Source Df Sum Dist Mean Dist F-ratio p-value
factors 15 8529.01958 568.60131 1.005 0.49
Within 3984 2253667.17960 565.67951
Total 3999 2262196.19918Ben
Reply all
Reply to author
Forward
0 new messages