registeration concept

[Behzad@UofA]

Hi,

I have a fundamental question. Any help will be appreciated.

Consider the following two shapes drawn in black. The shapes are two dimensional.

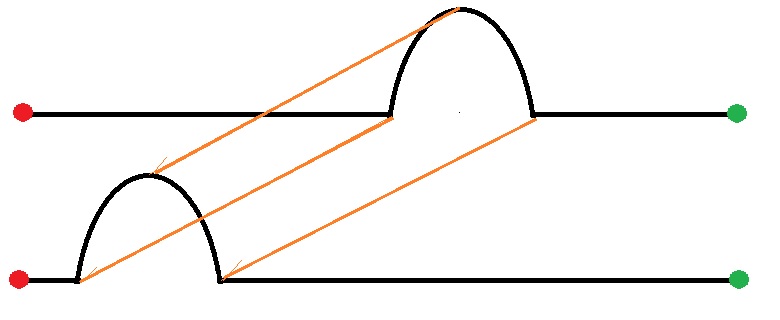
Assume the LM correspondence information as red points are in correspondence with each other, and also the green points with themselves.

Let's define a posterior GP having a Gaussian isotropic kernel to non-rigidly register the two shapes. The LM constraints are incorporated into the model.

My question is, what parameter or phenomenon guarantees that the GPMM registration leads to the point correspondence shown by the orange lines?

Thank you,

[Marcel Luethi]

HI Behzad

There are two possible things that could happen: Either the bump moves to the right, yielding the correspondence that you indicate in the drawing, or the bump in the reference is flattened and a new one is grown on the left side. Which one corresponds to the "correct" notion of correspondence depends on the particular application. 

What happens in Scalismo is difficult to say. It depends on the distance between the two bumps and the model that is used. A typical GP model enforces smoothness of the deformations. If the two bumps are close to each other, the deformation resulting from shifting one bump to coincide with the other is more smooth than one that is flattening one and growing a new one. If the bumps are far apart, the opposite is true. Both behaviours could, however, be enforced using landmarks.

Does that make sense?

Best regards,

Marcel

--
You received this message because you are subscribed to the Google Groups "scalismo" group.
To unsubscribe from this group and stop receiving emails from it, send an email to scalismo+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/scalismo/f6b18095-8d05-4bec-bf96-d037070abb40n%40googlegroups.com.

[Behzad Vafaeian]

Hi Marcel,

Thanks for your perfect answer.

It's good that we can enforce both applications using LM constraints in Scalismo.

Best,