Handling meshes with "inner" and "outer" surfaces

[Elon]

Hello Scalismo community,

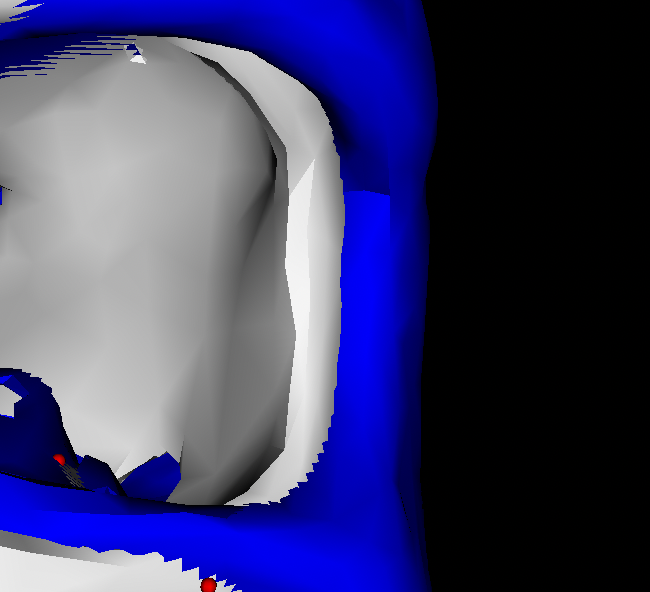
I've found that meshes with an “inner” and “outer” surface have a unique problem when sampling for correspondences – the closest point on the target mesh isn’t necessarily the correct surface (see attached line drawing). This results in a reconstruction with inner surfaces deformed to the outer surfaces or vice versa (example result in blue).

• I can imagine two possible solutions:
  
  1. Use a heuristic that compares the direction of normal vectors and throws out correspondences with a deviation of more than a certain number of degrees, or …
     
  2. When finding the closest point on the target mesh, only consider points along the surface normal of the randomly sampled point
     

Unfortunately, as a beginner in Scalismo, I require some advice for how to implement this in Scala code. Does anyone have experience with this? I'm wondering if the NormalDirectionSearchPointSampler class would be useful. Some code examples would be very helpful!

Much appreciated,

Elon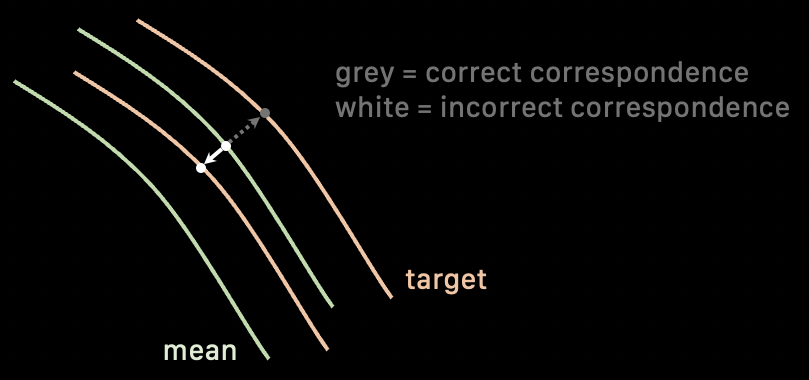

[Marcel Luethi]

Hi Elon

The following code snippet works for obtaining the normals:

val mesh : TriangleMesh[_3D] = ???
val point : Point[_3D] = ???

val surfaceNormal = mesh.operations.closestPointOnSurface(point) match {
    case ClosestPointInTriangle(point, dist, triangleId, bc) =>
        mesh.cellNormals(triangleId)
    case _ => 
        val idClosestVertex = mesh.pointSet.findClosestPoint(point).id
        mesh.vertexNormals(idClosestVertex)
}
There is also a possibility to find all the points that intersect any of the surfaces of the mesh:

val direction : EuclideanVector[_3D] = ???
val intersectionPoints = mesh.operations.getIntersectionPoints(point, direction)

Unfortunately these methods are currently not well documented. You might need to dive into the code or ask again if you encounter any problems.

Best wishes

Marcel

--
You received this message because you are subscribed to the Google Groups "scalismo" group.
To unsubscribe from this group and stop receiving emails from it, send an email to scalismo+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/scalismo/f381ae33-1f4f-4b4a-a791-846560de930cn%40googlegroups.com.

[Elon]

Hi Marcel,

Thank you for the example code. Is there a way to visualize these normals in Scalismo UI? The documentation says only some objects can be visualized in the UI, and EuclideanVector[_3D] does not appear to be one of them. I need to ensure that my heuristic is working correctly, since the results are not as expected.

Warm regards,

Elon

[Marcel Luethi]

You cannot visualize a EuclideanVector directly, as ScalismoUI would not know where to place it. You can only visualize vectors together with the domain, on which they are attached. The concept is called a DiscreteField. The following snippet shows how to visualize the normals of a mesh:

val normals = mesh.pointSet.pointIds.map(id => mesh.vertexNormals(id))
val normalField = DiscreteField3D(mesh, normals.toIndexedSeq)
ui.show(normalField, "normals")

Best regards,

Marcel

To view this discussion on the web visit https://groups.google.com/d/msgid/scalismo/1e36803c-e411-428b-bccc-d6980f235405n%40googlegroups.com.

[Elon]

Hi Marcel,

Thanks for the explanation! I visualized the normals and I'm fairly certain my heuristic is working now.

Cheers,

Elon

[Dennis Madsen]

Hi Elon, 

As for the heuristics you ask about. 3 different ones are mentioned in this paper: https://gravis.dmi.unibas.ch/publications/2007/CVPR07_Amberg.pdf  (section 4.4). 

I have some version of this implemented in scala as well: https://github.com/madsendennis/template-registration-with-scala/blob/main/src/main/scala/api/registration/utils/ClosestPointRegistrator.scala 

The "closestPointCorrespondence" function returns the closest point correspondence + a double set to 0.0 if there is a problem with some of the heuristic checks, otherwise 1.0.

Best

Dennis