How to convert complex_root_of to QQbar (algebraic number)

[Marcel Moosbrugger]

I am trying to convert "complex_root_of" expressions to algebraic numbers (elements in the field QQbar).  However, I get a "ValueError" with the message "to many values to unpack".

A minimal example would be:

from sage.all import *
from sympy import sympify

exp1 = sympify("CRootOf(x**2 + 1, 0)")._sage_()
exp2 = sympify("CRootOf(x**2 + 1, 1)")._sage_()
print(exp1)
print(exp2)
exp1 = QQbar(exp1)
exp2 = QQbar(exp2)
print(exp1)
print(exp2)

The context I am working in is: I have a tool that is currently written in python and sympy. I am trying to use the output of that tool to do some further computation using sage, and the output of the first tool may contain CRootOf expressions.

[William Stein]

Hi,

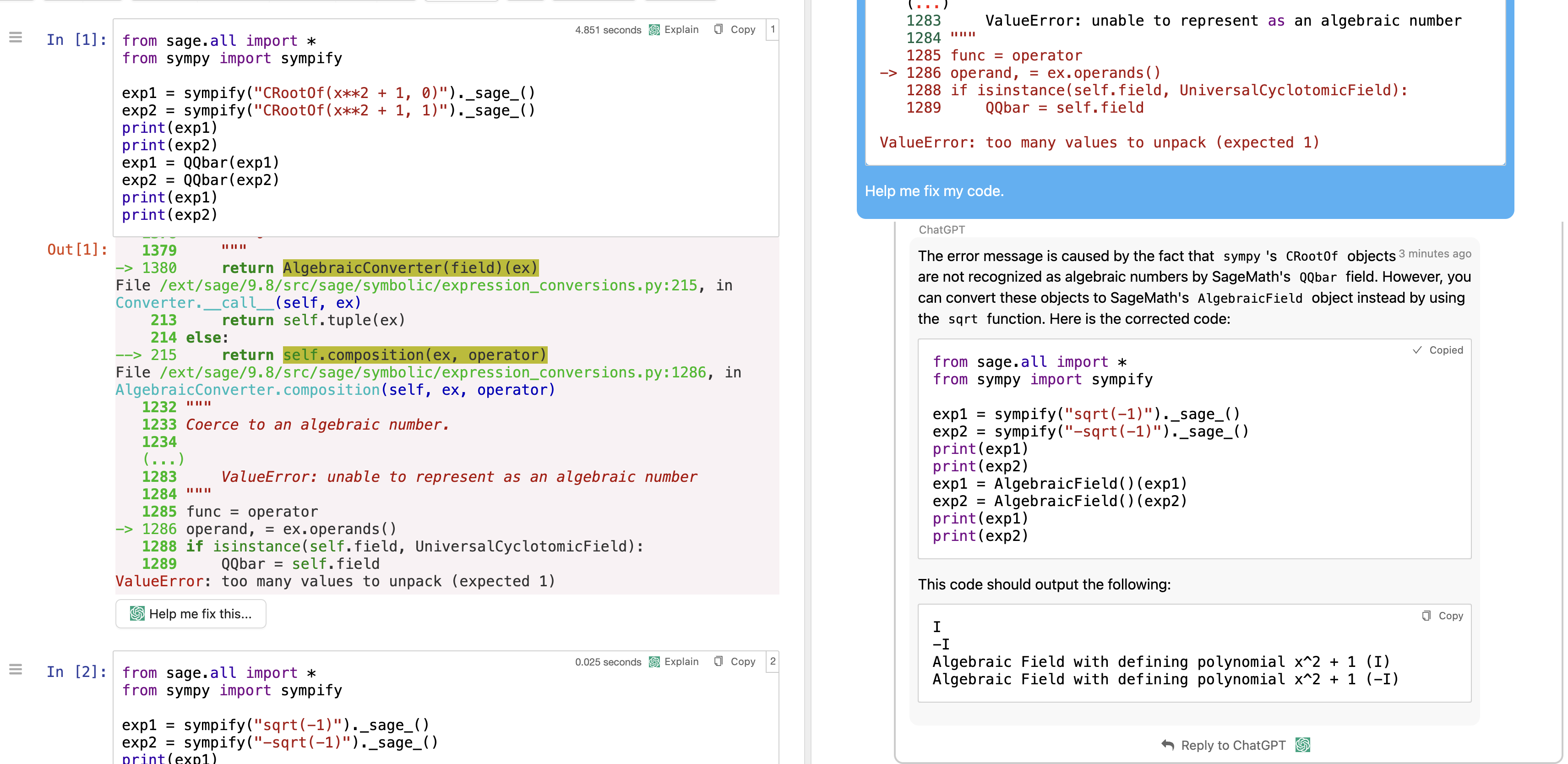
If you run exactly this code in a Sage Jupyter notebook in https://cocalc.com then click the big "Help me fix this..." button that appears after the error,
ChatGPT says in 8.3 seconds the following:

And Indeed, using AlgebraicField() instead does work:

from sage.all import *
from sympy import sympify

exp1 = sympify("sqrt(-1)")._sage_()
exp2 = sympify("-sqrt(-1)")._sage_()
print(exp1)
print(exp2)
exp1 = AlgebraicField()(exp1)
exp2 = AlgebraicField()(exp2)
print(exp1)
print(exp2)

Outputs I, -I, I, -I

You can then coerce the result into QQbar if you need to for some reason and this works:

sage: QQbar(exp1)

I

----

Meta comment -- I added this "Help me fix this..." feature to cocalc jupyter notebooks a week ago, and it's been extremely

popular with 1000+ uses a day.  It's exactly the sort of thing that ChatGPT can be very helpful with, given that Sage typical

outputs a massive scary stacktrace when anything goes wrong, and it's just a lot of mental effort to untangle it, especially given

the preparser.  ChatGPT is far from perfect, but it doesn't mind expending a lot of effort.     People also often get stuck and

very frustrated with Sage due to silly little things, e.g., accidentally capitalizing a function name, and chatgpt instantly points

out such things.     

You can reproduce the above exactly also at https://chat.openai.com/chat by using the prompt:

"I ran the following SageMath 9.8 code:

(put the code)

and it produced the following error message:

(put the error)

Help me fix my code."

However, I think people find seeing and error and just clicking once then seeing the result right in their notebook to be easier and less

disruptive of flow than a bunch of copy/paste.

--
You received this message because you are subscribed to the Google Groups "sage-support" group.
To unsubscribe from this group and stop receiving emails from it, send an email to sage-support...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/sage-support/4c8b1e6b-d77c-47bf-a02f-03c39e2261aan%40googlegroups.com.

--

William (http://wstein.org)

[Marcel Moosbrugger]

Hi William,

Thank you for your answer.

Unfortunately, this doesn't fix the problem. The code given by ChatGPT works because it turned the CRootOf expression into their explicit forms -i and i. In general, however, CRootOf expressions don't have such explicit forms.

When replacing the CRootOf expressions in my minimal example one can also just use QQbar instead of AlgebraicField() and it also works.

The sympy-based tool just spits out some CRootOf expressions, that don't have such explicit forms, in general.

Best,
Marcel

[Emmanuel Charpentier]

Le vendredi 31 mars 2023 à 15:19:51 UTC+2, William Stein a écrit :

[ Snip… ]

Meta comment -- I added this "Help me fix this..." feature to cocalc jupyter notebooks a week ago, and it's been extremely

popular with 1000+ uses a day.  It's exactly the sort of thing that ChatGPT can be very helpful with, given that Sage typical

outputs a massive scary stacktrace when anything goes wrong, and it's just a lot of mental effort to untangle it, especially given

the preparser.  ChatGPT is far from perfect, but it doesn't mind expending a lot of effort.     People also often get stuck and

very frustrated with Sage due to silly little things, e.g., accidentally capitalizing a function name, and chatgpt instantly points

out such things.     

You can reproduce the above exactly also at https://chat.openai.com/chat by using the prompt:

"I ran the following SageMath 9.8 code:

(put the code)

and it produced the following error message:

(put the error)

Help me fix my code."

However, I think people find seeing and error and just clicking once then seeing the result right in their notebook to be easier and less

disruptive of flow than a bunch of copy/paste.

Very nice ! With the usual reservation to take chatGPT’s answers with a grain of salt (sometomes iceberg-sized) : chatGPT conjured out of …err.., thin air, a matrix log function in Sage, and a matrix log function in Sympy ; the latter is only partially false, since Sympy’s Matrixes do have methods exp and log, the former is just plain wrong.

Do you think such a feature could be added to the Jupyter/Jupyterlab versions included in Sage ?

Or possibly to Jupyter/Juyterlab (i. e. upstream) ?

​

[William Stein]

Joke: maybe ChatGPT is robot from the future, and those functions will exist in a few years :-)

 

Do you think such a feature could be added to the Jupyter/Jupyterlab versions included in Sage ?

 

Or possibly to Jupyter/Juyterlab (i. e. upstream) ?

Yes, for sure; check out https://github.com/jupyterlab/jupyter-ai 

 

--
You received this message because you are subscribed to the Google Groups "sage-support" group.
To unsubscribe from this group and stop receiving emails from it, send an email to sage-support...@googlegroups.com.

To view this discussion on the web visit https://groups.google.com/d/msgid/sage-support/54ebf451-4b23-4f53-a29c-6b3ab1e2a790n%40googlegroups.com.

--

William (http://wstein.org)

[vdelecroix]

Dear Marcel,

It is a pity that this does not work more directly. Here is a work around to achieve what you want to do

sage: exp = sympify("CRootOf(x**5 + x + 1, 0)")
sage: sage_poly = QQ['x'](list(map(QQ, reversed(exp.poly.rep.rep))))
sage: sage_approx = RIF(exp.n()) + RIF(-1e-30, 1e-30)
sage: QQbar.polynomial_root(sage_poly, sage_approx)
-0.7548776662466928?

This will be fixed in https://github.com/sagemath/sage/pull/35414 and hopefully included in the next sage version.

Vincent

[William Stein]

Thanks Vincent! What version of Sage are you using? With sage-9.8 I get:

---

from sympy import sympify

exp = sympify("CRootOf(x**5 + x + 1, 0)")

sage_poly = QQ['x'](list(map(QQ, reversed(exp.poly.rep.rep))))

sage_approx = RIF(exp.n()) + RIF(-1e-30, 1e-30)

QQbar.polynomial_root(sage_poly, sage_approx)

Outputs:

ValueError: Refining interval that does not bound unique root!

----

> --
> You received this message because you are subscribed to the Google Groups "sage-support" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to sage-support...@googlegroups.com.

> To view this discussion on the web visit https://groups.google.com/d/msgid/sage-support/c4602f36-3cec-44e2-81a5-67dc38a50230n%40googlegroups.com.



--
William (http://wstein.org)

[Vincent Delecroix]

Will be fixed by https://github.com/sagemath/sage/pull/35414 (waiting for review)

On Sat, 1 Apr 2023 at 11:35, Vincent Delecroix <20100.d...@gmail.com> wrote:

PS: sorry in the last command "approx" should have been "sage_approx".

On Sat, 1 Apr 2023 at 11:35, Vincent Delecroix <20100.d...@gmail.com> wrote:

Dear Marcel,

It is a pity that this does not work more directly. Here is a work around to achieve what you want to do

sage: exp = sympify("CRootOf(x**5 + x + 1, 0)")
sage: sage_poly = QQ['x'](list(map(QQ, reversed(exp.poly.rep.rep))))
sage: sage_approx = RIF(exp.n()) + RIF(-1e-30, 1e-30)

sage: QQbar.polynomial_root(sage_poly, approx)
-0.7548776662466928?

Best

Vincent

To view this discussion on the web visit https://groups.google.com/d/msgid/sage-support/4987d26b-300c-46b8-bcd0-2bb0456713f2n%40googlegroups.com.

[Vincent Delecroix]

PS: sorry in the last command "approx" should have been "sage_approx".

On Sat, 1 Apr 2023 at 11:35, Vincent Delecroix <20100.d...@gmail.com> wrote:

Dear Marcel,

It is a pity that this does not work more directly. Here is a work around to achieve what you want to do

sage: exp = sympify("CRootOf(x**5 + x + 1, 0)")
sage: sage_poly = QQ['x'](list(map(QQ, reversed(exp.poly.rep.rep))))
sage: sage_approx = RIF(exp.n()) + RIF(-1e-30, 1e-30)
sage: QQbar.polynomial_root(sage_poly, approx)
-0.7548776662466928?

Best

Vincent

On Fri, 31 Mar 2023 at 19:12, Marcel Moosbrugger <marcelmo...@gmail.com> wrote:

To view this discussion on the web visit https://groups.google.com/d/msgid/sage-support/4987d26b-300c-46b8-bcd0-2bb0456713f2n%40googlegroups.com.

[Vincent Delecroix]

Dear Marcel,

It is a pity that this does not work more directly. Here is a work around to achieve what you want to do

sage: exp = sympify("CRootOf(x**5 + x + 1, 0)")
sage: sage_poly = QQ['x'](list(map(QQ, reversed(exp.poly.rep.rep))))
sage: sage_approx = RIF(exp.n()) + RIF(-1e-30, 1e-30)
sage: QQbar.polynomial_root(sage_poly, approx)
-0.7548776662466928?

Best

Vincent

On Fri, 31 Mar 2023 at 19:12, Marcel Moosbrugger <marcelmo...@gmail.com> wrote:

To view this discussion on the web visit https://groups.google.com/d/msgid/sage-support/4987d26b-300c-46b8-bcd0-2bb0456713f2n%40googlegroups.com.

[Marcel Moosbrugger]

Thank you all for your help!

I got the same error as William, but it pointed me into the right direction. I found a way how to get the unique bounding interval of the root in sympy and convert this interval to a sage interval. It is not the prettiest solution but the following works for me:

from sage.all import *
from sympy import sympify

from sage.symbolic.expression_conversions import polynomial

expr = sympify("CRootOf(x**2 + 1, 0)")
complex_interval = expr._get_interval()
real_from = Rational(str(complex_interval.ax))._sage_()
real_to = Rational(str(complex_interval.bx))._sage_()
im_from = Rational(str(complex_interval.ay))._sage_()
im_to = Rational(str(complex_interval.by))._sage_()
sage_interval = CIF(RIF(real_from, real_to), RIF(im_from, im_to))
min_poly = polynomial(expr.expr._sage_(), base_ring=QQ)
algebraic_number = QQbar.polynomial_root(min_poly, sage_interval)

[Hongyi Zhao]

I tried the above steps, but ChatGPT failed to fix the error:

Chatbot:
The issue with your code is that you are trying to convert SymPy expressions to elements of the algebraic number field `QQbar`, but the `QQbar` constructor does not support SymPy expressions. Instead, you should use the `AlgebraicNumber` constructor to create algebraic numbers from SymPy expressions, and then you can convert them to elements of `QQbar`.

Here's the corrected code:

```

from sage.all import *
from sympy import sympify

exp1 = sympify("CRootOf(x**2 + 1, 0)")._sage_()
exp2 = sympify("CRootOf(x**2 + 1, 1)")._sage_()
print(exp1)
print(exp2)

exp1 = AlgebraicNumber(exp1)
exp2 = AlgebraicNumber(exp2)

print(exp1)
print(exp2)
exp1 = QQbar(exp1)
exp2 = QQbar(exp2)
print(exp1)
print(exp2)

```

This should output the following:

```
complex_root_of(x^2 + 1, 0)
complex_root_of(x^2 + 1, 1)
1*I
-1*I
1*I
-1*I
```

Note that the imaginary unit `I` is represented as `1*I` or `-1*I` in `QQbar`, depending on the sign of the imaginary part.