Possible bugs in SR
104 views
Skip to first unread message
Emmanuel Charpentier
Jul 7, 2021, 4:46:33 PM7/7/21
to sage-support
The same ask.sagemath question may have revealed two different bugs in symbolics handling.
Input interpretation.
Raw input, with spaces, indents and newlines :
f(x) = (3/174465461165747500*pi*(-1750000*I*pi*x^3 - 31250000*(224*pi + 45*sqrt(448*pi + 2025) + 2025)*x^2
+ 17500000000000000*I*pi*x)
*sqrt(92821652156334811582567480952850314403/10*pi^2/(224*pi + 45*sqrt(448*pi + 2025) + 2025)
+ 98489794142024498175862287197250000*pi*sqrt(448*pi + 2025)
/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 7713517620898636162808584411766250000*pi
/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 659225266976959904108326638192187500*sqrt(448*pi + 2025)
/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 29665137013963195684874698718648437500
/(224*pi + 45*sqrt(448*pi + 2025) + 2025))
/(63*pi^2*x^4 - (504000*I*pi^2 + 67500*I*pi*(sqrt(448*pi + 2025) + 45))*x^3
- 3000000*(560224*pi^2 + 45*pi*(sqrt(448*pi + 2025) + 45))*x^2 + 8400000000000000000000*pi^2
- (-5040000000000000*I*pi^2 - 675000000000000*I*pi*(sqrt(448*pi + 2025) + 45))*x))
Single-line reformatted code (deleting blanks, indents and newlines, adding a space before ‘+’ and ‘-‘)
g(x) = (3/174465461165747500*pi*(-1750000*I*pi*x^3 - 31250000*(224*pi + 45*sqrt(448*pi + 2025) + 2025)*x^2 + 17500000000000000*I*pi*x)*sqrt(92821652156334811582567480952850314403/10*pi^2/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 98489794142024498175862287197250000*pi*sqrt(448*pi + 2025)/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 7713517620898636162808584411766250000*pi/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 659225266976959904108326638192187500*sqrt(448*pi + 2025)/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 29665137013963195684874698718648437500/(224*pi + 45*sqrt(448*pi + 2025) + 2025))/(63*pi^2*x^4 - (504000*I*pi^2 + 67500*I*pi*(sqrt(448*pi + 2025) + 45))*x^3 - 3000000*(560224*pi^2 + 45*pi*(sqrt(448*pi + 2025) + 45))*x^2 + 8400000000000000000000*pi^2 - (-5040000000000000*I*pi^2 - 675000000000000*I*pi*(sqrt(448*pi + 2025) + 45))*x))
Notwithstanding formatting differences, these functions should be equal ; they are not :
sage: f(1).n()
418409.917305474 + 1.28757494213663e11*I
sage: g(1).n()
1.39111866114058e-12 + 6.95559330500736e-6*I
factor bug
sage: F = f.real()^2 + f.imag()^2
sage: Ff = (f.real()^2 + f.imag()^2).factor()
sage: G = g.real()^2 + g.imag()^2
sage: Gf = (g.real()^2 + g.imag()^2).factor()
sage: F(1).n()
1.65784923163565e22
sage: Ff(1).n()
4.77205703148314e29
sage: G(1).n()
4.83802782246652e-11
sage: Gf(1).n()
0.00139260822082924
These two bugs may have a common origin in SR code (pynac comes to mind).
My question is : how to file bugs about these ones, which seem extremely serious (silent errors in basic symbolics abilities) ?
Nils Bruin
Jul 7, 2021, 7:01:44 PM7/7/21
to sage-support
I think the main problem in f(x) is a preparser problem: https://trac.sagemath.org/ticket/11621
The other problems could just be numerical instability. The normal precision is 53 bits, which is good for about 16 decimal digits. The constants in the formula are more than that, so if there is significant cancellation, it may be this is just expected. Perhaps try and evaluatie with a larger precision? .n(500) or so? If the answers are now closer then it could just be numerical. The factored expression should give a different evaluation scheme for what is presumably the same quantity.
Emmanuel Charpentier
Jul 8, 2021, 12:49:18 PM7/8/21
to sage-support
Dear Nils, dear list,
Le jeudi 8 juillet 2021 à 01:01:44 UTC+2, Nils Bruin a écrit :
I think the main problem in f(x) is a preparser problem: https://trac.sagemath.org/ticket/11621
This is likely ; I don't see how to check this, but I'll accept it for now.
The other problems could just be numerical instability. The normal precision is 53 bits, which is good for about 16 decimal digits. The constants in the formula are more than that, so if there is significant cancellation, it may be this is just expected. Perhaps try and evaluatie with a larger precision? .n(500) or so? If the answers are now closer then it could just be numerical. The factored expression should give a different evaluation scheme for what is presumably the same quantity.
This does not happen : the discrepancy does not change when raising the precision.
I still think that something is wroing in SR handling, and I'll try to exhibit it in an understandable way. Stay tuned...
Thanks a lot !
Nils Bruin
Jul 8, 2021, 1:39:48 PM7/8/21
to sage-support
On Thursday, 8 July 2021 at 09:49:18 UTC-7 Emmanuel Charpentier wrote:
Dear Nils, dear list,Le jeudi 8 juillet 2021 à 01:01:44 UTC+2, Nils Bruin a écrit :I think the main problem in f(x) is a preparser problem: https://trac.sagemath.org/ticket/11621This is likely ; I don't see how to check this, but I'll accept it for now.
You can check it in the following way, which makes it behave as the problem on the ticket: move the plus at the start of the second line to the end of the first line. Now the preparser mangles the string into an ungrammatical one, rather than a grammatical one with a different meaning.
Emmanuel Charpentier
Jul 9, 2021, 6:20:37 PM7/9/21
to sage-support
Same setup as before :
x = var('x', domain='positive')
f(x) = (3/174465461165747500*pi*(-1750000*I*pi*x^3 - 31250000*(224*pi + 45*sqrt(448*pi + 2025) + 2025)*x^2 + 17500000000000000*I*pi*x)*sqrt(92821652156334811582567480952850314403/10*pi^2/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 98489794142024498175862287197250000*pi*sqrt(448*pi + 2025)/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 7713517620898636162808584411766250000*pi/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 659225266976959904108326638192187500*sqrt(448*pi + 2025)/(224*pi + 45*sqrt(448*pi + 2025) + 2025) + 29665137013963195684874698718648437500/(224*pi + 45*sqrt(448*pi + 2025) + 2025))/(63*pi^2*x^4 - (504000*I*pi^2 + 67500*I*pi*(sqrt(448*pi + 2025) + 45))*x^3 - 3000000*(560224*pi^2 + 45*pi*(sqrt(448*pi + 2025) + 45))*x^2 + 8400000000000000000000*pi^2 - (-5040000000000000*I*pi^2 - 675000000000000*I*pi*(sqrt(448*pi + 2025) + 45))*x))
In order to understand the structure of the expression, one can replace numerical constants by symbolic ones :
def Symb(ex, MaxPower=None):
# Replace numerical constants by sumbols in a symbolic expression
# (Sagemath version)
def Nums(ex):
# Collect numerical constants of a numerical expression
# (Sagemath version)
if ex._sympy_().is_number: return [ex]
if ex.is_symbol() : return []
# Uniq give a shmewhat orchidoclasic version...
return uniq(reduce(union, map(Nums, ex.operands())))
L = Nums(ex)
# Optionally, keep small integer powers (often exponents)
if MaxPower is not None:
L = [u for u in L if not (u.is_integer() and u.abs() <= MaxPower)]
V = var("c", n=len(L))
D = dict(zip(L, V))
iD = dict(zip(V, L))
E = ex.subs(D)
return tuple([E, D, iD])
E, D, iD = Symb(f(x))
Unfortunately, the result is nonsensical (a constant) :
E
iD[c2]
c2
-100/69786184466299
The same algorithm can be coded using sympy tools and expressions :
def SymbS(ex, MaxPower=None):
# Collect numerical constants of a numerical expression
# (Sympy-in-Sagemath version)
def Nums(ex):
# Collect numerical constants of a numerical expression
# (Sagemath version)
# This *expected* to give results slightly different from
# the Sage version : x.is_numeric() ==> x._sympy_().is_number, but
# the inverse is not true...
from functools import reduce
if ex.is_number: return set([ex])
if ex.is_symbol: return set()
return reduce(lambda a, b:a.union(b), map(Nums, ex.args))
import sympy
L = Nums(ex)
if MaxPower is not None:
L = [u for u in L if not (u.is_integer and sympy.Abs(u) <= MaxPower)]
else: L = list(L)
V = sympy.var("s:%d"%len(L))
D = dict(zip(L, V))
iD = dict(zip(V, L))
E = ex.subs(D)
return tuple([E, D, iD])
SE, SD, SiD = SymbS(f(x)._sympy_(), MaxPower=4)
SE
-100*s10*s12*(s10*s3*s4*x + s10*s4*s5*x**3 + s14*s15*x**2)/(69786184466299*s13 - 69786184466299000000*s16*x**2 - 104679276699448500*s6*x**3 + 1046792766994485000000000000*s6*x + 1465509873792279*s9*x**4)
The results make sense (notwhistanding the presence of some numerical constants in the result, possibly due to premature or delayed numerical simplifications), and are numerically consistent with f :
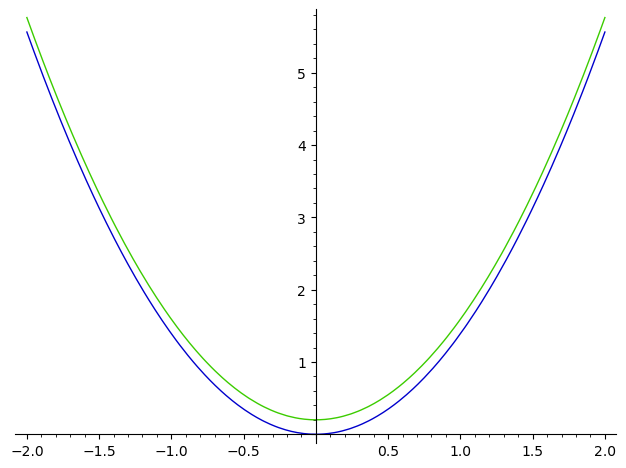
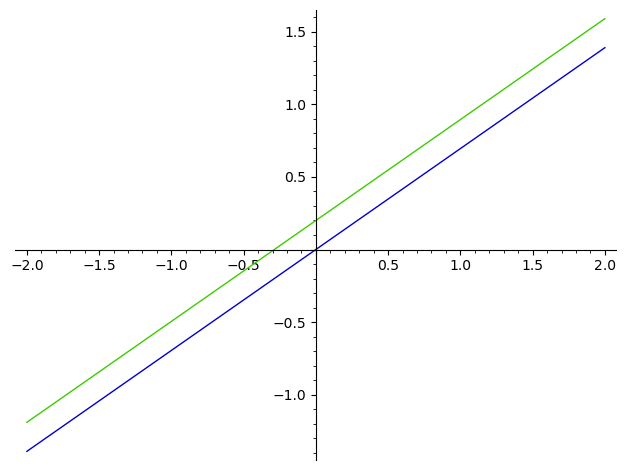
One can check that using the numerical constants created by sympy to create a Sage expressin also give a nonsensical constant function :
D2D=dict(zip(SiD.keys(),var("k", n=len(SiD))))
f(x).subs({u:D2D[SD[u]] for u in SD.keys()})
k2
Conversely, using the numerical constants created by sage to create a sympy expression (possibly converted to sage) gives sensible results :
import sympy
D2D2=dict(zip(map(lambda u:u._sympy_(), list(D.keys())),sympy.var("l:%d"%len(D))))
f(x)._sympy_().subs(D2D2)._sage_()
-100*(l11*l13*x^l5 + l3*l7*x + l4*l7*x^l6)*(-69786184466299000000*l14*x^l5 + 1046792766994485000000000000*l18*x - 104679276699448500*l18*x^l6 + 1465509873792279*l9*x^l8 + 69786184466299*l17)^l1*l16*l7
Therefore, one can conclude that Sage's handling of expressions is buggy in this case.
Questions :
* Does this deserve filing a ticket ?
* Is so, how to file it efficiently ?
Reply all
Reply to author
Forward
0 new messages
