Strange torsion in modular symbols
112 views
Skip to first unread message
Preston Wake
May 24, 2020, 3:16:43 PM5/24/20
to sage-nt
Hello,
I've found that the modular symbols code in Sage may detect interesting examples of torsion modular forms. For example:
G=DirichletGroup(13);
e=G.gen()^6; # e has order 2
M=ModularSymbols(e,2,-1); # M is 0
ep=e.change_ring(GF(3));
Mp=ModularSymbols(ep,2,-1); # Mp is one-dimensional
I think this is coming from the famous counterexample to the naive version of Serre's conjecture: there is a mod-3 modular form of weight 2 and level 13 with quadratic character such that any lift to characteristic zero has non-quadratic character. This is something peculiar to mod-p forms for p=2 or 3.
But it also sometimes gives confusing results:
M=ModularSymbols(7,8,1).cuspidal_subspace(); # M has dimension 3
Mp=ModularSymbols(7,8,1,GF(5)).cuspidal_subspace(); # M has dimension 4
I don't think this should happen: mod-5 modular forms of weight 8 and level Gamma0(7) should lift to characteristic 0 forms of the same type. I assume that what is happening is that Mp is not really computing H^1(X_0(7),\F_5)^+, which is I thing I think modular symbols should be.
Math question: Where is this extra dimension coming from? Does it have any interesting number theoretic meaning?
Sage question: Is this a bug? Should Sage warn us that, with finite-field coefficients, ModularSymbols might not be computing the thing I think it is computing?
Best wishes,
Preston
William Stein
May 24, 2020, 3:38:07 PM5/24/20
to sage-nt
computing. This is not a bug. What it computes is precisely
defined, meaningful and in some cases may be much faster than
computing what you want. However, to use it as input to a
something else, you have to understand what it is really doing...
It would be reasonable to add to the docs here
https://doc.sagemath.org/html/en/reference/modsym/sage/modular/modsym/modsym.html
to say something like "ModularSymbols in characteristic p in Sage
might not compute what you think they compute. Do not make
assumptions about them without also consulting the Sage source code
and understanding what is actually implemented (which is approximately
using Manin symbols and the same relations that are used in
characteristic 0)."
> Best wishes,
> Preston
>
> --
> You received this message because you are subscribed to the Google Groups "sage-nt" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to sage-nt+u...@googlegroups.com.
> To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/18758bbb-b636-4db9-815f-ebe79354fbb4%40googlegroups.com.
--
William (http://wstein.org)
Preston Wake
May 24, 2020, 6:32:39 PM5/24/20
to sag...@googlegroups.com
On Sun, May 24, 2020 at 3:38 PM William Stein <wst...@gmail.com> wrote:
On Sun, May 24, 2020 at 12:16 PM Preston Wake <presto...@gmail.com> wrote:
>
> Hello,
>
> I've found that the modular symbols code in Sage may detect interesting examples of torsion modular forms. For example:
>
> G=DirichletGroup(13);
> e=G.gen()^6; # e has order 2
> M=ModularSymbols(e,2,-1); # M is 0
> ep=e.change_ring(GF(3));
> Mp=ModularSymbols(ep,2,-1); # Mp is one-dimensional
>
> I think this is coming from the famous counterexample to the naive version of Serre's conjecture: there is a mod-3 modular form of weight 2 and level 13 with quadratic character such that any lift to characteristic zero has non-quadratic character. This is something peculiar to mod-p forms for p=2 or 3.
>
> But it also sometimes gives confusing results:
>
> M=ModularSymbols(7,8,1).cuspidal_subspace(); # M has dimension 3
> Mp=ModularSymbols(7,8,1,GF(5)).cuspidal_subspace(); # M has dimension 4
>
> I don't think this should happen: mod-5 modular forms of weight 8 and level Gamma0(7) should lift to characteristic 0 forms of the same type. I assume that what is happening is that Mp is not really computing H^1(X_0(7),\F_5)^+, which is I thing I think modular symbols should be.
>
> Math question: Where is this extra dimension coming from? Does it have any interesting number theoretic meaning?
>
> Sage question: Is this a bug? Should Sage warn us that, with finite-field coefficients, ModularSymbols might not be computing the thing I think it is computing?
>
ModularSymbols are indeed not computing what you think it is
computing.
Is what I want already implemented somewhere in Sage? Can I compute the space of mod-p modular forms? (Especially in cases where this is different from modular forms mod p.)
-Preston
This is not a bug. What it computes is precisely
defined, meaningful and in some cases may be much faster than
computing what you want. However, to use it as input to a
something else, you have to understand what it is really doing...
It would be reasonable to add to the docs here
https://doc.sagemath.org/html/en/reference/modsym/sage/modular/modsym/modsym.html
to say something like "ModularSymbols in characteristic p in Sage
might not compute what you think they compute. Do not make
assumptions about them without also consulting the Sage source code
and understanding what is actually implemented (which is approximately
using Manin symbols and the same relations that are used in
characteristic 0)."
> Best wishes,
> Preston
>
> --
> You received this message because you are subscribed to the Google Groups "sage-nt" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to sage-nt+u...@googlegroups.com.
> To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/18758bbb-b636-4db9-815f-ebe79354fbb4%40googlegroups.com.
--
William (http://wstein.org)
--
You received this message because you are subscribed to the Google Groups "sage-nt" group.
To unsubscribe from this group and stop receiving emails from it, send an email to sage-nt+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/CACLE5GCm9BO-%2B8YmV5HPovKb__WQaBsgbd1kQ3n%2BQYLBkQYCcg%40mail.gmail.com.
John Cremona
May 26, 2020, 3:34:44 AM5/26/20
to sage-nt
Computing mod p modular forms is quite tricky, and has not in general
been implemented in Sage (or anywhere else). As well as the valid
points William has already made, consider the following: suppose one
wants to find all mod-2 modular forms which are ductions of
characteristic zero modular forms. Take a char. 0 newforms with
coefficients in Q(sqrt(5)). the coefficients are algebraic integers,
hence in Z[(1+sqrt(5))/2]. That ring has no prime ideals with
quotient GF(2) (since 2 is inert in that field) so you think that
there is no mod-2 reduction of the newform. BUT in fact, in this case
(which can happen) the coefficients lie in the non-maximal order
Z[sqrt(5)], and that ring does have a prime of index 2, so there is a
GF(2) modular form obtained by reduction (replacing sqrt(5) as a
coefficient by 1 mod 2).
In 2018 I was part of a small group starting to do this sort of thing
systematically (the others are Samuele Anni, Andrew Sutherland, David
Roberts and Peter Bruin). We made a start only. One intention is to
make a database of mod-ell modular forms in the LMFDB. One reason for
the delay in making progress on this was that at the time we started,
the LMFDB database of classical modular forms was rather small and not
so well organised. That situation is now vastly improved (see
https://www.lmfdb.org/ModularForm/GL2/Q/holomorphic/ and the preprint
https://arxiv.org/abs/2002.04717 for many details of the large-scale
computations behind that).
John
> To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/CAOjp0GGOEE%2BMeY43o_%2BVb3VGSe_aEHUyfGg-CSf_fW%2BH-VPsDg%40mail.gmail.com.
been implemented in Sage (or anywhere else). As well as the valid
points William has already made, consider the following: suppose one
wants to find all mod-2 modular forms which are ductions of
characteristic zero modular forms. Take a char. 0 newforms with
coefficients in Q(sqrt(5)). the coefficients are algebraic integers,
hence in Z[(1+sqrt(5))/2]. That ring has no prime ideals with
quotient GF(2) (since 2 is inert in that field) so you think that
there is no mod-2 reduction of the newform. BUT in fact, in this case
(which can happen) the coefficients lie in the non-maximal order
Z[sqrt(5)], and that ring does have a prime of index 2, so there is a
GF(2) modular form obtained by reduction (replacing sqrt(5) as a
coefficient by 1 mod 2).
In 2018 I was part of a small group starting to do this sort of thing
systematically (the others are Samuele Anni, Andrew Sutherland, David
Roberts and Peter Bruin). We made a start only. One intention is to
make a database of mod-ell modular forms in the LMFDB. One reason for
the delay in making progress on this was that at the time we started,
the LMFDB database of classical modular forms was rather small and not
so well organised. That situation is now vastly improved (see
https://www.lmfdb.org/ModularForm/GL2/Q/holomorphic/ and the preprint
https://arxiv.org/abs/2002.04717 for many details of the large-scale
computations behind that).
John
Preston Wake
May 26, 2020, 9:32:45 AM5/26/20
to sag...@googlegroups.com
Thanks for this answer, John. I think it would be very useful to add mod-ell modular forms to LMFDB! Your example about non-maximal orders is enlightening -- I see that LMFDB now lists "coefficient ring index" for newforms, so you can see if the order is maximal or not.
To me this seems like a strange way to compute mod-p modular forms, though. Since the mod-p Hecke algebra is (usually) not semi-simple, you miss out on a lot of extra structure by only computing the field-valued points. You also might end up over-counting: two characteristic-zero newforms might have the same reduction. For example, in level Gamma0(11) and weight 2 with p=5, there's only one mod-5 form, but it should be counted with multiplicity two.
If you're only interested in modular forms that lift to characteristic zero, instead of computing Galos-orbits and then reducing them, couldn't you just take the matrices representing the characteristic-zero Hecke operators and reduce those matrices modulo p? This would give you the Hecke algebra acting on modular forms mod p, and modular forms are just functionals on this algebra. The different eigenspaces would give you newforms, and the size of the generalized eigenspaces would give you the multiplicities. I guess the drawback is that it's not so easy to see which characteristic-zero newform reduces to which mod-p form.
Regarding the documentation: when I look at https://doc.sagemath.org/html/en/reference/modsym/sage/modular/modsym/modsym.html, it's not easy for me to see what the mathematical definition of "modular symbol" being used is. Given that different authors use the term "modular symbols" to mean different things, it might be useful to add to the documentation either the definition or a link to a place where the definition can be read. It seems like ModularSymbols(G,k,base_ring=R) is computing the object called ) in Definition 1.23 here: https://wstein.org/books/modform/modform/modular_symbols.html.
in Definition 1.23 here: https://wstein.org/books/modform/modform/modular_symbols.html.
Best,
Preston
To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/CAD0p0K4wkwh07fH6HoGOgbWf3WwndPfPHtOn2YCo9bEhwuTipQ%40mail.gmail.com.
John Cremona
May 26, 2020, 10:01:06 AM5/26/20
to sage-nt
On Tue, 26 May 2020 at 14:32, Preston Wake <presto...@gmail.com> wrote:
Thanks for this answer, John. I think it would be very useful to add mod-ell modular forms to LMFDB! Your example about non-maximal orders is enlightening -- I see that LMFDB now lists "coefficient ring index" for newforms, so you can see if the order is maximal or not.
Indeed. That's why it is there. Also having a Z-basis for the coefficient ring (which is an order, just not the maximal order) means that we can store and display the Hecke eigenvalues as integer vectors, and we use LLL-reducition to make those smaller. This is al ot better than expressing the as polynomials in a field generator (especially if that generator is take to be a_2, say, since the index of Z[a_2] in the coefficient order can be huge).
To me this seems like a strange way to compute mod-p modular forms, though. Since the mod-p Hecke algebra is (usually) not semi-simple, you miss out on a lot of extra structure by only computing the field-valued points. You also might end up over-counting: two characteristic-zero newforms might have the same reduction. For example, in level Gamma0(11) and weight 2 with p=5, there's only one mod-5 form, but it should be counted with multiplicity two.
That was just one source we used to start with. There's a lot more to do on that project.
If you're only interested in modular forms that lift to characteristic zero, instead of computing Galos-orbits and then reducing them, couldn't you just take the matrices representing the characteristic-zero Hecke operators and reduce those matrices modulo p? This would give you the Hecke algebra acting on modular forms mod p, and modular forms are just functionals on this algebra. The different eigenspaces would give you newforms, and the size of the generalized eigenspaces would give you the multiplicities. I guess the drawback is that it's not so easy to see which characteristic-zero newform reduces to which mod-p form.
You have just sketched exactly what some version of my code does. Having the Hecke algebra presented with matrices gives you a lot more information than just the list of their characteristic polynomials.
Regarding the documentation: when I look at https://doc.sagemath.org/html/en/reference/modsym/sage/modular/modsym/modsym.html, it's not easy for me to see what the mathematical definition of "modular symbol" being used is. Given that different authors use the term "modular symbols" to mean different things, it might be useful to add to the documentation either the definition or a link to a place where the definition can be read. It seems like ModularSymbols(G,k,base_ring=R) is computing the object calledin Definition 1.23 here: https://wstein.org/books/modform/modform/modular_symbols.html.
Agreed! Regarding your "different authors" comment, let me just say that my 1981 thesis was titled "Modular Symbols" but that my supervisor (Birch) and I never actually agreed on what they were. Enough said,
John
To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/CAOjp0GFcz1pQftYag3qz7-d0XY%3DinVJ0kYyoEbLTd8cYYFCWzQ%40mail.gmail.com.
Preston Wake
May 26, 2020, 12:35:56 PM5/26/20
to sag...@googlegroups.com
Regarding the documentation: when I look at https://doc.sagemath.org/html/en/reference/modsym/sage/modular/modsym/modsym.html, it's not easy for me to see what the mathematical definition of "modular symbol" being used is. Given that different authors use the term "modular symbols" to mean different things, it might be useful to add to the documentation either the definition or a link to a place where the definition can be read. It seems like ModularSymbols(G,k,base_ring=R) is computing the object calledin Definition 1.23 here: https://wstein.org/books/modform/modform/modular_symbols.html.
I realized that this is wrong: ModularSymbols(G,k,base_ring=R) is not computing ) . According to the definition
. According to the definition =%5Cmathbb%7BM%7D%5Fk(G)%5Cotimes%5F%5Cmathbb%7BZ%7D%09R) and
and ) is a free
is a free  -module of finite rank, so
-module of finite rank, so %09=%09%7B%5Crm%09dim%7D%5F%5Cmathbb%7BQ%7D%09%5Cmathbb%7BM%7D%5Fk(G;%5Cmathbb%7BQ%7D)) for any prime
for any prime 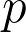 . This is contradicted by my example.
. This is contradicted by my example.
Does anyone know what ModularSymbols(G,k,base_ring=R) is computing? Is maybe it is %5FG%09%5Cotimes%5F%5Cmathbb%7BZ%7D%09R) , where subscript-G means coinvariants?
, where subscript-G means coinvariants?
-Preston
William Stein
May 29, 2020, 1:00:44 AM5/29/20
to sage-nt
On Tue, May 26, 2020 at 9:35 AM Preston Wake <presto...@gmail.com> wrote:
> Does anyone know what ModularSymbols(G,k,base_ring=R) is computing? Is maybe it ismort, where subscript-G means coinvariants?
It uses a characteristic 0 presentation involving Manin symbols, but
does the linear algebra over R instead of QQ. If you know enough
about
a situation (e.g., you are interesting in p=5 say and the dimension is
the same) then this can be extremely efficient and useful. But for
some
small values of p, e.g., p=2 or 3, you can end up with an object that
is basically useless (e.g., "Hecke operators" on it don't commute).
Kevin Buzzard and I once worried about this problem when writing [1]
(see Remark 1.2 on page 268).
-- William
[1] https://wstein.org/papers/artin/buzzard-stein.pdf
--
William (http://wstein.org)
> Does anyone know what ModularSymbols(G,k,base_ring=R) is computing? Is maybe it ismort, where subscript-G means coinvariants?
It uses a characteristic 0 presentation involving Manin symbols, but
does the linear algebra over R instead of QQ. If you know enough
about
a situation (e.g., you are interesting in p=5 say and the dimension is
the same) then this can be extremely efficient and useful. But for
some
small values of p, e.g., p=2 or 3, you can end up with an object that
is basically useless (e.g., "Hecke operators" on it don't commute).
Kevin Buzzard and I once worried about this problem when writing [1]
(see Remark 1.2 on page 268).
-- William
[1] https://wstein.org/papers/artin/buzzard-stein.pdf
--
William (http://wstein.org)
Preston Wake
May 31, 2020, 9:58:14 AM5/31/20
to sag...@googlegroups.com
Thanks for your answer, William! I think I understand now what ModularSymbols is computing. Let me say it in a different way, to see how it compares to the group denoted \bM_k(G;R) in the Definition 1.23 of your book (https://wstein.org/books/modform/modform/modular_symbols.html). The command ModularSymbols(G,k,base_ring=R) is first computing a free abelian group M given by the Manin symbols, and then it computes a subgroup M' of M such that:
(i) M' maps to zero in \bM_k(G), and
(ii) M/M' \otimes \Q is equal to \bM_k(G;\Q)/
Then it returns the R-module M/M' \otimes R. Currently this is only implemented when R is a field.
How does this output compare to \bM_k(G;R)? Well, we know that the Manin symbols M generate \bM_k(G) integerally (this is Proposition 1.24), so by (i) there is a surjection M/M' -->> \bM_k(G). Since \bM_k(G) is a free ZZ-module of finite rank, (ii) implies that the kernel of this surjection is exactly the torsion subgroup of M/M'. Hence, when R is a characteristic-zero field, then the output is actually equal to \bM_k(G;R), but when R has characteristic p, the output is equal to \bM_k(G;R) if and only if M/M' is p-torsion-free. If M/M' has p-torsion, then probably the output is useless (?).
Some questions:
- Why isn't ModularSymbols(G,k,base_ring=R) implemented for rings (like R=ZZ)? It seems like, given what is already there, it wouldn't be too hard to ask it to output (M/M')/(torsion) (although this may be hard for it to actually compute...)
- For characteristic-p fields, why does Sage output M/M' \otimes R instead of (M/M')/(torsion) \otimes R? The obvious reason is the one William says: outputing M/M' \otimes R may be much faster. But isn't this anathema to what Sage normally does? By default, Sage normally makes you do the more mathematically-meaningful thing, rather than the faster thing.
But for
some
small values of p, e.g., p=2 or 3, you can end up with an object that
is basically useless (e.g., "Hecke operators" on it don't commute).
I don't think this torsion phenomenon is just about small primes. Are you saying that when p is large, the resulting space is not basically useless? For example:
ModularSymbols(5,16,1); # M has dimension 9
Mp=ModularSymbols(5,16,1,GF(13)); #Mp has dimension 10;
Is this because 13 is small, in this case? Or are you saying that this Mp is not "basically useless"? If so, what is its basic use?
Best,
Preston
William Stein
May 31, 2020, 11:26:36 AM5/31/20
to sage-nt
On Sun, May 31, 2020 at 6:58 AM Preston Wake <presto...@gmail.com> wrote:
>
> Thanks for your answer, William! I think I understand now what ModularSymbols is computing. Let me say it in a different way, to see how it compares to the group denoted \bM_k(G;R) in the Definition 1.23 of your book (https://wstein.org/books/modform/modform/modular_symbols.html). The command ModularSymbols(G,k,base_ring=R) is first computing a free abelian group M given by the Manin symbols, and then it computes a subgroup M' of M such that:
> (i) M' maps to zero in \bM_k(G), and
> (ii) M/M' \otimes \Q is equal to \bM_k(G;\Q)/
> Then it returns the R-module M/M' \otimes R. Currently this is only implemented when R is a field.
>
> How does this output compare to \bM_k(G;R)? Well, we know that the Manin symbols M generate \bM_k(G) integerally (this is Proposition 1.24), so by (i) there is a surjection M/M' -->> \bM_k(G). Since \bM_k(G) is a free ZZ-module of finite rank, (ii) implies that the kernel of this surjection is exactly the torsion subgroup of M/M'. Hence, when R is a characteristic-zero field, then the output is actually equal to \bM_k(G;R), but when R has characteristic p, the output is equal to \bM_k(G;R) if and only if M/M' is p-torsion-free. If M/M' has p-torsion, then probably the output is useless (?).
>
That sounds right.
>
> Thanks for your answer, William! I think I understand now what ModularSymbols is computing. Let me say it in a different way, to see how it compares to the group denoted \bM_k(G;R) in the Definition 1.23 of your book (https://wstein.org/books/modform/modform/modular_symbols.html). The command ModularSymbols(G,k,base_ring=R) is first computing a free abelian group M given by the Manin symbols, and then it computes a subgroup M' of M such that:
> (i) M' maps to zero in \bM_k(G), and
> (ii) M/M' \otimes \Q is equal to \bM_k(G;\Q)/
> Then it returns the R-module M/M' \otimes R. Currently this is only implemented when R is a field.
>
> How does this output compare to \bM_k(G;R)? Well, we know that the Manin symbols M generate \bM_k(G) integerally (this is Proposition 1.24), so by (i) there is a surjection M/M' -->> \bM_k(G). Since \bM_k(G) is a free ZZ-module of finite rank, (ii) implies that the kernel of this surjection is exactly the torsion subgroup of M/M'. Hence, when R is a characteristic-zero field, then the output is actually equal to \bM_k(G;R), but when R has characteristic p, the output is equal to \bM_k(G;R) if and only if M/M' is p-torsion-free. If M/M' has p-torsion, then probably the output is useless (?).
>
> Some questions:
> - Why isn't ModularSymbols(G,k,base_ring=R) implemented for rings (like R=ZZ)? It seems like, given what is already there, it wouldn't be too hard to ask it to output (M/M')/(torsion) (although this may be hard for it to actually compute...)
research. Other than that, it could be done.
There is some very closely related functionality that is implemented:
sage: M = ModularSymbols(7,8,1).cuspidal_submodule()
sage: M.integral_hecke_matrix(5)
[-320460 285880 67032]
[-212550 189650 44448]
[-626400 558720 131056]
Try M.integral[tab] to find several other related commands. The
above is a matrix for T_5 on Modular symbols over ZZ (mod any
torsion, just to be clear). You could reduce it modulo 5 and that may
be what you're interested in:
sage: T5 = M.integral_hecke_matrix(5).change_ring(GF(5))
sage: T5.fcp()
(x + 4) * x^2
sage: T5.minimal_polynomial().factor()
x * (x + 4)
https://share.cocalc.com/share/df81e09e5b8f16f28b3a2e818dcdd4560e7818ae/support/2020-05-28-modular-over-R.ipynb?viewer=share
> - For characteristic-p fields, why does Sage output M/M' \otimes R instead of (M/M')/(torsion) \otimes R? The obvious reason is the one William says: outputing M/M' \otimes R may be much faster. But isn't this anathema to what Sage normally does? By default, Sage normally makes you do the more mathematically-meaningful thing, rather than the faster thing.
I implemented all this about 15 years ago before anybody else used
Sage...
>> But for
>> some
>> small values of p, e.g., p=2 or 3, you can end up with an object that
>> is basically useless (e.g., "Hecke operators" on it don't commute).
>
> I don't think this torsion phenomenon is just about small primes. Are you saying that when p is large, the resulting space is not basically useless?
and trivial character in that remark.
> For example:
> ModularSymbols(5,16,1); # M has dimension 9
> Mp=ModularSymbols(5,16,1,GF(13)); #Mp has dimension 10;
> Is this because 13 is small, in this case? Or are you saying that this Mp is not "basically useless"? If so, what is its basic use?
that 10 dimensional space...
> Best,
> Preston
>
>
> --
> You received this message because you are subscribed to the Google Groups "sage-nt" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to sage-nt+u...@googlegroups.com.
> To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/CAOjp0GFPB%3DJeLw7HXqpvuG6UzOuWePAudwJ%2B01R%3D5Z7Zg6tBew%40mail.gmail.com.
>
>
> --
> You received this message because you are subscribed to the Google Groups "sage-nt" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to sage-nt+u...@googlegroups.com.
--
William (http://wstein.org)
David Loeffler
Jun 15, 2020, 4:13:39 AM6/15/20
to sage-nt, Preston Wake
I don't know if anyone's still following this thread -- I only just saw it myself.
As William says, Sage's modular symbols code for mod p coefficients doesn't compute the thing you might expect (the homology with mod p coefficients). However, there is some old code floating around on the Sage trac server by GeorgSWeber here:
which, I believe, *does* compute the homology of the modular curve mod p. I have no idea if it still works, or if it's useful. It's 9 years old, but that part of Sage has not changed much since then, so there's at least a non-zero chance the code might still be workable.
Best wishes, David
To view this discussion on the web visit https://groups.google.com/d/msgid/sage-nt/CACLE5GAqSj51jjQsKMb2Fe2aKahsPr8x1NOYPUD9hWPGNCF2Vg%40mail.gmail.com.
Reply all
Reply to author
Forward
0 new messages
