Definite Integral wrong
175 views
Skip to first unread message
Nico Guth
Aug 2, 2020, 12:26:42 PM8/2/20
to sage-devel
Hi,
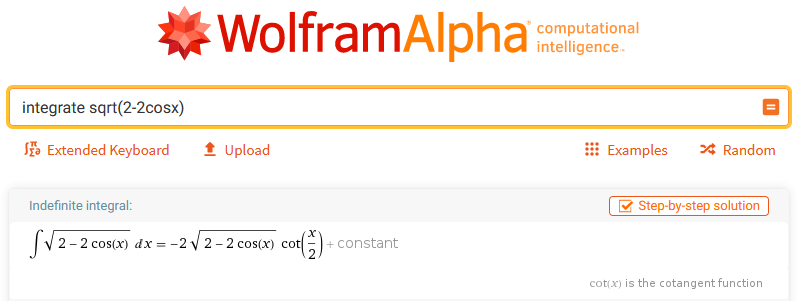
I discovered a bug, where a definite integral is calculated wrong!
WolframAlpha result for comparison.
Code:
integrate(sqrt(2-2*cos(x)),x,0,2*pi)
integrate(sqrt(2-2*cos(x)),x,0,2*pi)
Also if I type show() instead of print() SageMathCell just doesn't show anything.
Also the form in which the indefinite integral is given is not very pretty.
WolframAlpha does a much better job simplifying.


Dima Pasechnik
Aug 3, 2020, 4:50:12 AM8/3/20
to sage-devel
This is a well-known bug in Sage. A workaround is to set the domain to "real":
sage: maxima_calculus.eval('domain: real');
sage: integrate(sqrt(2-2*cos(x)),x,0,2*pi) # correct answer
8
sage: integrate(sqrt(2-2*cos(x)),x,0,2*pi) # correct answer
8
sage: maxima_calculus.eval('domain: complex'); # restore the state back
sage: integrate(sqrt(2-2*cos(x)),x,0,2*pi) # now here the result is again wrong, of course
0
sage: integrate(sqrt(2-2*cos(x)),x,0,2*pi) # now here the result is again wrong, of course
0
--
You received this message because you are subscribed to the Google Groups "sage-devel" group.
To unsubscribe from this group and stop receiving emails from it, send an email to sage-devel+...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/sage-devel/487d0db8-5711-41a8-a7d4-1548286b5573n%40googlegroups.com.
Emmanuel Charpentier
Aug 4, 2020, 4:56:16 AM8/4/20
to sage-devel
BTW :
sage: integrate(sqrt(2-2*cos(x)),x, algorithm="fricas")
-2*(cos(x) + 1)*sqrt(-2*cos(x) + 2)/sin(x)
sage: integrate(sqrt(2-2*cos(x)),x, algorithm="mathematica_free")
-2*sqrt(-2*cos(x) + 2)*cot(1/2*x)
Both are visually (on plot) and numerically correct ; both differentiate to expressions very hard to show equal to the original function.
HTH,
Le lundi 3 août 2020 10:50:12 UTC+2, Dima Pasechnik a écrit :
This is a well-known bug in Sage. A workaround is to set the domain to "real":sage: maxima_calculus.eval('domain: real');
sage: integrate(sqrt(2-2*cos(x)),x,0,2*pi) # correct answer
8sage: maxima_calculus.eval('domain: complex'); # restore the state back
sage: integrate(sqrt(2-2*cos(x)),x,0,2*pi) # now here the result is again wrong, of course
0
On Sun, Aug 2, 2020 at 5:26 PM Nico Guth <nico.j...@gmail.com> wrote:
Hi,I discovered a bug, where a definite integral is calculated wrong!WolframAlpha result for comparison.Code:
integrate(sqrt(2-2*cos(x)),x,0,2*pi)Also if I type show() instead of print() SageMathCell just doesn't show anything.Also the form in which the indefinite integral is given is not very pretty.WolframAlpha does a much better job simplifying.--
You received this message because you are subscribed to the Google Groups "sage-devel" group.
To unsubscribe from this group and stop receiving emails from it, send an email to sage-...@googlegroups.com.
rjf
Aug 5, 2020, 2:59:01 PM8/5/20
to sage-devel
There are two square roots. In this (classic) integration example/bug, a choice has
to be made. You know that 4 has two square roots, -2 and 2.
The integrand, which also can be rewritten as sqrt ( 4-4*cos(x/2)^2) , has 2 square roots.
Therefore there are two potential different values for the integral. Any answer
that supplies only one answer is wrong.
NicoJG
Aug 5, 2020, 3:49:37 PM8/5/20
to sage-devel
@rjf Isn't the square root defined to be positive?
Sure: x^2=y <=> x=+/-sqrt(y)
Sure: x^2=y <=> x=+/-sqrt(y)
But I think you would never consider f(x):=sqrt(x) to have the codomain of all negative numbers.
At least I would expect a CAS to interpret a square root to be positive.
Dave Morris
Aug 5, 2020, 4:00:01 PM8/5/20
to sage-devel
I agree with the general analysis, but I think the statement "Any answer that supplies only one answer is wrong." goes too far. It may be the case that sage works inherently in the complex domain, and is unable to understand that elementary calculus and certain other fields want to remain in the real domain, but it would not be "wrong" to have a program that operates differently. It is not "wrong" to work in the real domain and understand that "\sqrt{2}" means 1.414... (the "principal square root"), not -1.414... Indeed, I think sage would need to be able to do to be really useful for most 1st semester calculus students. In this situation, there is a unique correct answer, so returning two answers is "wrong".
Nils Bruin
Aug 5, 2020, 7:31:45 PM8/5/20
to sage-devel
On Wednesday, August 5, 2020 at 12:49:37 PM UTC-7, NicoJG wrote:
@rjf Isn't the square root defined to be positive?
Sure: x^2=y <=> x=+/-sqrt(y)
But I think you would never consider f(x):=sqrt(x) to have the codomain of all negative numbers.
With complex numbers, there's no concept of negative numbers. A choice of principal branch of sqrt indeed selects only half on the complex plane, but it's not at all clear which choice is most appropriate. Both upper half plane and right half plane have their uses.
At least I would expect a CAS to interpret a square root to be positive.
Certainly not in a complex setting. That's actually one of the main things that "domain: complex" vs. "domain: real" changes in maxima.
Michael Orlitzky
Aug 5, 2020, 8:20:28 PM8/5/20
to sage-...@googlegroups.com
On 2020-08-05 15:49, NicoJG wrote:
> @rjf Isn't the square root defined to be positive?
> Sure: x^2=y <=> x=+/-sqrt(y)
> But I think you would never consider f(x):=sqrt(x) to have the codomain
> of all negative numbers.
> At least I would expect a CAS to interpret a square root to be positive.
>
If you think of sqrt() as a function on the real numbers, then sure. The
> @rjf Isn't the square root defined to be positive?
> Sure: x^2=y <=> x=+/-sqrt(y)
> But I think you would never consider f(x):=sqrt(x) to have the codomain
> of all negative numbers.
> At least I would expect a CAS to interpret a square root to be positive.
>
problem with this (and many other functions) is that we really have no
idea what the domain and codomain are. The documentation is silent on
the matter. This comes up especially often in the context of sqrt()
because we all learned square roots in elementary school and therefore
arrive with some (soon to be violated) expectation of how they work.
To do things right, you really need to know the (co)domain of a function
before you do anything else with it. Of course, we don't want high
school students to have to learn modules and algebras before they can
create 2x^2 + y^3, so we wind up faking it with things like the symbolic
ring, on which sqrt() acts... somehow. How exactly it should act no one
can say for sure, and that's ultimately what leads to this problem.
Samuel Lelievre
Aug 5, 2020, 8:49:45 PM8/5/20
to sage-devel
2020-08-05 18:59:01 UTC, rjf:
>
> There are two square roots. In this (classic) integration
> example/bug, a choice has to be made. You know that 4 has
> two square roots, -2 and 2. The integrand, which also can
> be rewritten as sqrt ( 4-4*cos(x/2)^2) , has 2 square
> roots. Therefore there are two potential different values
> for the integral. Any answer that supplies only one answer
> is wrong.
Would you agree that:
- There is a map f from the real interval [0, +oo)
to itself, mapping each element to its square.
- That map is a continuous increasing bijection.
- It has a compositional inverse F which is also
a continuous increasing bijection
from the real interval [0, +oo) to itself.
The map f is commonly called "square" and the map F
is commonly called "square root". The notation
$x \mapsto x^2$ is often used for f, while the
"radical" notation $x \mapsto \sqrt{x}$ is often
used for F. In computer algebra systems, the name
`sqrt` is frequently used for F, while f rarely gets
named at all, with `sq`, `sqr`, `square` possibly
infrequently used.
You seem to be objecting strongly (please confirm)
about one or several of the following:
- the naming "square" for f or "square root" for F
- the "radical" notation $\sqrt$ for F
- using `sqrt` for F in computer algebra systems
If so, do you have any suggestion for
- admissible ways to name them?
- admissible mathematical notation?
- admissible naming in computer algebra systems?
These maps are sometimes useful to consider.
Computing their integrals along some segments
of the interval [0, +oo) is sometimes needed.
Is it admissible to compute such integrals?
How can we talk about these computations?
For sure,
- There is also a map g from the interval (-oo, +oo)
to the interval [0, +oo), mapping each element
to its square;
this map is surjective; under it, 0 has a single
preimage while all other real numbers have two;
it is therefore not bijective; the inverse relation
"sends" 0 to itself and any positive real y
to the two opposite reals whose square y is.
- There is also a map h from the field of complex numbers
to itself, mapping each element to its square;
this map is surjective; under it, 0 has a single
preimage while all other complex numbers have two;
it is therefore not bijective; the inverse relation
"sends" 0 to itself and any nonzero complex number z
to the two opposite complex numbers whose square z is.
I have observed that frequently, discussing the map F
or the computation of its integral along a subinterval
of [0, +oo) leads to lengthy discussions about the map g
or the map h and their inverse relations.
I am wondering about any appropriate vocabulary that can
be used in order to discuss the maps f and F without having
to discuss the maps g and h and their inverse relations.
The maps g and h and their inverse relations are important.
It is sometimes important not to forget that they are not
bijective and that most elements in their range have two
preimages under them. But sometimes that's not the topic,
and people are just discussing the map F.
Markus Wageringel
Aug 6, 2020, 4:07:11 AM8/6/20
to sage-devel
Even if there are two possible choices, the result of the definite integral should be ±8, not 0. It is rather strange to pick the positive square root for half the integral and then (discontinuously) the negative one for the other half.
rjf schrieb am Mittwoch, 5. August 2020 um 20:59:01 UTC+2:
kcrisman
Aug 6, 2020, 7:38:42 AM8/6/20
to sage-devel
On Thursday, August 6, 2020 at 4:07:11 AM UTC-4 Markus Wageringel wrote:
Even if there are two possible choices, the result of the definite integral should be ±8, not 0. It is rather strange to pick the positive square root for half the integral and then (discontinuously) the negative one for the other half.There is a ticket for exactly this integral, by the way: https://trac.sagemath.org/ticket/17183.
And one upstream for Maxima: https://sourceforge.net/p/maxima/bugs/2823/
Though what I think it particularly surprising here is that this used to be an abs_integrate problem, which I thought we had disabled - apparently it persists (now? or maybe always did) under domain:complex. I'd be grateful if someone could update that Maxima ticket with precise conditions where it fails.
rjf
Aug 6, 2020, 6:56:29 PM8/6/20
to sage-devel
I suppose you could have some function like RPSqrt, for realpositivesqrt
which maps from non-negative reals to non-negative reals.
It would be an error to type RPSqrt(x) unless x were guaranteed to be oretty much
explicitly in [0,oo].
Sqrt(x^2) under some conditions might be considered RPSqrt(x) and then x.
Sqrt((-x)^2) would also be x. I think abs(x) is a mistake, but people differ on this.
Alternatively, something like this (in Maxima) rootsof(g^2-x^2, g).
This notation embodies the two roots g=x and g=-x. Doing calculations
with this is generally not supported.. In Maxima, it comes up
only in the answers for integration if you first say integrate_use_rootsof: true.
A more general notation is available in other systems. For
example, you might want to give some index number to the particular
roots so that you could say rootsof(g^2-x^2,g,1) * rootsof(g^2-x^2,g,2) = -x^2.
rootsof(g^2-4,g) is a way of notating {-2,2} in effect, in systems that
support something like rootsof. See how far you can push this. Can you
take log ( )?
RJF
Reply all
Reply to author
Forward
0 new messages