ar1 sometimes fits what looks like an intercept-only model?

[KTM]

Hello,

I am exploring some hierarchical time-series models using INLA. I have noticed something strange. Here is a basic example:

A simple ar1 model 

mod = function(y) {
  require(INLA) 
  z = 1:length(y) 
  myData = list(y=y,z=z) 
  formula = y ~ f(z,model="ar1",constr=T) 
  m = inla(formula,data=myData,family="gaussian",  
            control.predictor=list(link=1))
  return(m) 
}  

Some simple simulated data:
n = 100
theta = arima.sim(n=n,list(ar=0.75),sd=0.7) +10 ; plot(theta)
y = rnorm(n,mean=theta,sd=0.1)   ; lines(y,col="darkblue",lwd=2) 
m = mod(y)

lines(m$summary.fitted.values[,1],col="green",lwd=2)

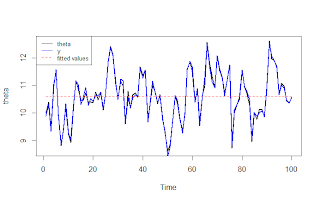
Sometimes this works as expected, with the rho parameter retrieved, and the fitted values are nearly identical to the original y data:

Then other times, I generate another data set in the exact same manner (re-run this code), and the fitted values are essentially a straight-line, like an intercept-only model:

When this happens, the rho parameter on the ar1 is always estimated to be negative, when it is supposed to be positive. My guess is I've done something weird in the simulation, but when I use arima() in R I can always retrieve the rho parameter without any problems on the exact same data that INLA has issues with. I've also tried very similar models in JAGS and never have this same problem. This problem only becomes weirder when I try to explore Poisson time-series counts. Any advice/ideas on what I'm doing wrong would be hugely appreciated! 

Thanks so much,

Kathryn

[INLA help]

On Tue, 2014-12-09 at 09:03 -0800, KTM wrote:
>
> Hello,
>
>
> I am exploring some hierarchical time-series models using INLA. I have
> noticed something strange. Here is a basic example:
>
>
> A simple ar1 model
> mod = function(y) {
> require(INLA)
> z = 1:length(y)
> myData = list(y=y,z=z)
> formula = y ~ f(z,model="ar1",constr=T)
> m = inla(formula,data=myData,family="gaussian",
> control.predictor=list(link=1))
> return(m)
> }
>
> Some simple simulated data:
> n = 100
> theta = arima.sim(n=n,list(ar=0.75),sd=0.7) +10 ; plot(theta)
> y = rnorm(n,mean=theta,sd=0.1) ; lines(y,col="darkblue",lwd=2)
> m = mod(y)
> lines(m$summary.fitted.values[,1],col="green",lwd=2)
>

> When this happens, the rho parameter on the ar1 is always estimated to
> be negative, when it is supposed to be positive. My guess is I've done
> something weird in the simulation, but when I use arima() in R I can
> always retrieve the rho parameter without any problems on the exact
> same data that INLA has issues with. I've also tried very similar
> models in JAGS and never have this same problem. This problem only
> becomes weirder when I try to explore Poisson time-series counts. Any
> advice/ideas on what I'm doing wrong would be hugely appreciated!

Hi

what happens is that it goes to a different interpretation of the data,
and not the one you want. the main issue is the inital values, which for
some datasets makes it goes to the wrong place. the source for the
problem is the intercept, which is 10, in your case. which simply fools
the optimizer, and then it fail to turn.

simply setting a higher initial value for the data precision will fix
the problem, and runs fine for (at least) 1000 trials.

H

mod = function(y) {
require(INLA)
z = 1:length(y)
myData = list(y=y,z=z)
formula = y ~ f(z,model="ar1",constr=T)
m = inla(formula,data=myData,family="gaussian",

control.family = list(
hyper = list(prec = list(initial = 10))),
control.predictor=list(link=1))
}

for(i in 1:1000) {

n = 100
theta = arima.sim(n=n,list(ar=0.75),sd=0.7)

y = rnorm(n,mean=theta,sd=0.1)
m = mod(y)
err = mean(abs(y - m$summary.fitted.values[,"mean"]))
if (err > 0.01) print(c(i, err))
}





--
Håvard Rue
he...@r-inla.org

[KTM]

That is great, thank you so much. So this is a prior on the precision of the Gaussian likelihood? How would this translate when I have multiple likelihoods, e.g., 

  m = inla(formula, data=myData, family=rep("gaussian",3),  

           control.family = list(hyper = list(prec = list(initial=c(10,10,10) )) )

  

gives error  Argument 'control.family' does not match length(family)= 3

Also, what about say for Poisson where the initial values are not available hyperparameters? (As far as I know). Could other initial values (in the ar1?) cause similar problems? 

[INLA help]

On Tue, 2014-12-09 at 11:29 -0800, KTM wrote:
> That is great, thank you so much. So this is a prior on the
> precision of the Gaussian likelihood? How would this translate
> when I have multiple likelihoods, e.g.,
>
> m = inla(formula, data=myData, family=rep("gaussian",3),
> control.family = list(hyper = list(prec =
> list(initial=c(10,10,10) )) )
>
> gives error Argument 'control.family' does not match length(family)=
> 3

it should, the format is

control.family = list(list(),list(),list())

where each list() is for each family. so you have do

control.family = list(
list(hyper = list(prec = list(initial = 10))),
list(hyper = list(prec = list(initial = 10))),
list(hyper = list(prec = list(initial = 10))))

which I havn't checked...

> Also, what about say for Poisson where the initial values are not
> available hyperparameters? (As far as I know). Could other initial
> values (in the ar1?) cause similar problems?

yes, its kind of the same issue with the precision there.

H

--
Håvard Rue
he...@r-inla.org