Order of accuracy analysis in ACM
75 views
Skip to first unread message
mkamra
Oct 6, 2020, 10:47:28 AM10/6/20
to PyFR Mailing List
Hello Everyone,
I have a question regarding the order of accuracy of the ACM method; Have you done any tests using the method of manufactured solutions ( published or otherwise) ?
I tried the 2D taylor green benchmark but the order of accuracy I am getting is nowhere near what it should be. When comparing with exact solution I used the solution points directly not the subdivided solution in the vtu file to avoid interpolation issues polluting the order of accuracy
Also regarding the ACM, how would one obtain the residual of the continuity and momentum equations? Pseudo-stats only report the change between two consecutive pseudo iterations
Regards,
M Kamra
Vincent, Peter E
Oct 6, 2020, 10:51:07 AM10/6/20
to mkamra, PyFR Mailing List
Hi M Karma,
Could you provide more details of the test case, the way your are obtaining the order of accuracy, and the results that you are getting.
Thanks
Peter
Professor of Computational Fluid Dynamics and EPSRC Fellow
Department of Aeronautics
Imperial College London
South Kensington
London
SW7 2AZ
UK
Department of Aeronautics
Imperial College London
South Kensington
London
SW7 2AZ
UK
--
You received this message because you are subscribed to the Google Groups "PyFR Mailing List" group.
To unsubscribe from this group and stop receiving emails from it, send an email to pyfrmailingli...@googlegroups.com.
To view this discussion on the web, visit https://groups.google.com/d/msgid/pyfrmailinglist/fc58961d-02b2-4e7b-a05b-62af91f93537n%40googlegroups.com.
Mohamed M. Kamra
Oct 6, 2020, 11:38:57 AM10/6/20
to pyfrmai...@googlegroups.com
Hi,
Thanks for the prompt response
I followed the case illustrated in Cox et al article
It is a double periodic 2D manufactured solution case, the u, v source terms are evaluated using Mathematica
I attach the ini file here
The Re = 10
I calculated the order of accuracy in the manner described in the article which is fairly straightforward
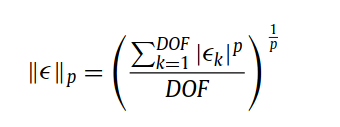
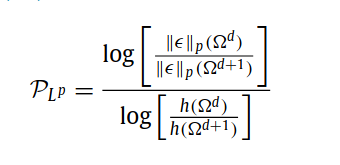
where eps_k is the difference between the exact solution and the numerical solution.
I used the same meshes resolutions as the article 4x4, 8x8, 16x16, 32x32 with double periodic bcs generated using gmsh
For now, I am only trying to verify the spatial accuracy so following the article's example I am using very small dt
I tried different zeta values, different pseudo-dt,, more pseudo-niters-max going as high as 50 which is killing my performance
the only part I did not mess with is the LDG beta and tau
I double-checked the source terms several times but it seems okay
So I am not sure what could be the problem.
Appreciate your help.
M Kamra
Vincent, Peter E
Oct 6, 2020, 9:49:00 PM10/6/20
to Mohamed M. Kamra, pyfrmai...@googlegroups.com
Hi Mohamed,
I am a little confused as to the test case you are using.
The 2D TGV case in the paper you reference does not seem to use a method of manufactured solutions, it just solves the regular NS equations without a source term?
Apologies if I missed something.
Peter
Professor of Computational Fluid Dynamics and EPSRC Fellow
Department of Aeronautics
Imperial College London
South Kensington
London
SW7 2AZ
UK
Department of Aeronautics
Imperial College London
South Kensington
London
SW7 2AZ
UK
On 6 Oct 2020, at 16:38, Mohamed M. Kamra <mo7amme...@gmail.com> wrote:
Hi,Thanks for the prompt responseI followed the case illustrated in Cox et al articleIt is a double periodic 2D manufactured solution case, the u, v source terms are evaluated using Mathematica
I attach the ini file hereThe Re = 10
I calculated the order of accuracy in the manner described in the article which is fairly straightforward
<image.png>
To view this discussion on the web, visit https://groups.google.com/d/msgid/pyfrmailinglist/CAHrgCm7h18kXm-dUA%2BmfZH%2BK8bw1kfbpBnEdLyxORnpfV%3DFvrw%40mail.gmail.com.
<tg2d.ini>
Mohamed M. Kamra
Oct 6, 2020, 10:23:30 PM10/6/20
to Vincent, Peter E, pyfrmai...@googlegroups.com
Hi Peter,
You're right. I left the source term in the ini file because it may not evaluate to zero depending on the choice of the length scale in the Reynolds number (since the domain is not a unit square). When the length scale is chosen to be 1 ( Re = 1/nu) which is the case in all of our simulations so far, then the source term vanishes and that's what's used in the ini file attached.
So I don't think that the source term is the cause of the problem. I removed it now just in case but I got the exact same results.
Regards,
Mohamed Kamra
Vincent, Peter E
Oct 6, 2020, 10:28:29 PM10/6/20
to Mohamed M. Kamra, pyfrmai...@googlegroups.com
So what orders of accuracy do you get?
Mohamed M. Kamra
Oct 6, 2020, 11:28:13 PM10/6/20
to Vincent, Peter E, pyfrmai...@googlegroups.com
When solver solver.order = 4
4x4 : Mesh DOFs = 400 Variable: U Error L1Norm = 0.000114383
Variable: U Error L2Norm = 0.000132731
8x8 : Mesh DOFs = 1600
Variable: U Error L1Norm = 3.8896e-05
Variable: U Error L2Norm = 4.86379e-05
16x16 : Mesh DOFs = 6400
Variable: U Error L1Norm = 3.90541e-05
Variable: U Error L2Norm = 4.82179e-05
32x32 : Mesh DOFs = 25600
Variable: U Error L1Norm = 3.91447e-05
Variable: U Error L2Norm = 4.81805e-05
Between the first two meshes, it is not even second order, after the order becomes almost 0!
Vvisualizing the error shows high error everywhere, specifically at high gradient areas
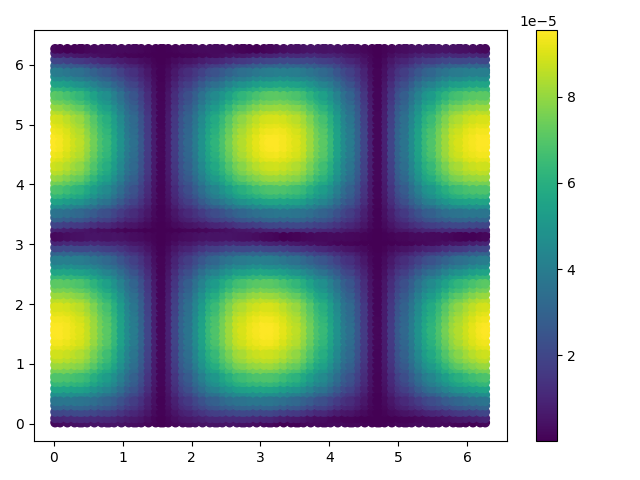
Error distribution of U for Mesh 16x16 , order 4.0
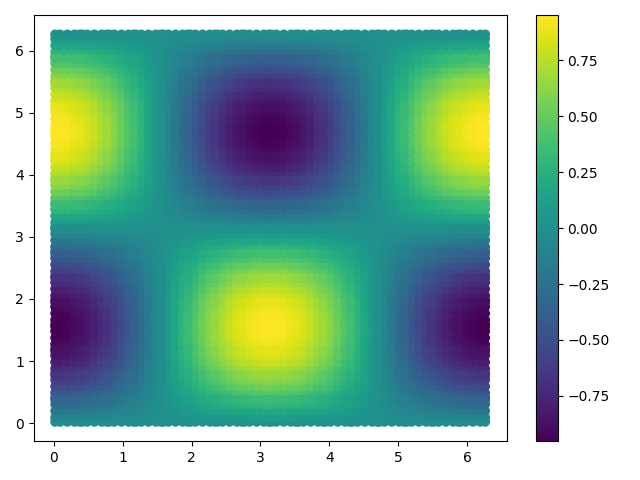
Distribution of U Numerical solution for Mesh 16x16 , order 4.0
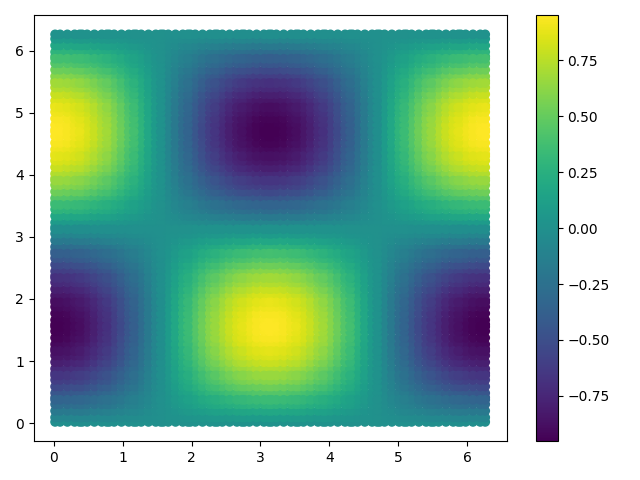
Distribution of U Exact solution for Mesh 16x16 , order 4.0
Vincent, Peter E
Oct 7, 2020, 9:21:22 AM10/7/20
to Mohamed M. Kamra, pyfrmai...@googlegroups.com
So it looks like errors saturate at 8x8 and don’t go down.
So maybe due to the time integration?
How small is the dt that you are using, and do the numbers change when you reduce it further?
Regarding:
I tried different zeta values, different pseudo-dt,, more pseudo-niters-max going as high as 50 which is killing my performance
Can you send plots of how the pseudo residuals are converging in each dt?
What do you mean quantitatively by ‘killing performance’
Are you using local pseudo dt and PMG etc. for the inner iterations, or just plain RK4?
<image.png>Error distribution of U for Mesh 16x16 , order 4.0
<image.png>
Distribution of U Numerical solution for Mesh 16x16 , order 4.0
Mohamed M. Kamra
Oct 7, 2020, 12:25:08 PM10/7/20
to Vincent, Peter E, pyfrmai...@googlegroups.com
How small is the dt that you are using, and do the numbers change when you reduce it further?
The time step dt = 0.001 when decreased to 5e-4 and even 1e-4 the change in error is no more 1%
pseudo-niters-max = 50 , using p-multigrid with vermiere pseudo integration
I tried local-pi but it was either unstable or ineffective perhaps I need to do needs some fine-tuning of my chosen parameters
What do you mean quantitatively by ‘killing performance’Are you using local pseudo dt and PMG etc. for the inner iterations, or just plain RK4?
As for the matter of performance, using p-multigrid with pseudo-niters-max of 50 yields a wall clock time of 6 hours if dt is taken as low as 1e-4 for 8x8 mesh to run only 1s ( GPU utilization at less than 15%)
Can you send plots of how the pseudo residuals are converging in each dt?
As for the residuals:
p : 5e-5 ~ 1e-4
uv: 1e-6 ~ 1e-7
For reference, the residual history data and the corresponding ini file can be downloaded from the following link
I included residual history for 0.25s only
Freddie Witherden
Oct 7, 2020, 1:06:17 PM10/7/20
to Mohamed M. Kamra, Vincent, Peter E, pyfrmai...@googlegroups.com
Can you confirm what order of accuracy you get if you just perform your study on the solution produced by PyFR at t = 0 (so the initial condition)?
Regards, Freddie.
On 7 Oct 2020, at 11:25, Mohamed M. Kamra <mo7amme...@gmail.com> wrote:
To view this discussion on the web, visit https://groups.google.com/d/msgid/pyfrmailinglist/CAHrgCm7afPGjP05gUWL_Ebusg53CrX7Cd85gUJXxsunvdWt67Q%40mail.gmail.com.
Mohamed M. Kamra
Oct 7, 2020, 1:19:42 PM10/7/20
to Freddie Witherden, Vincent, Peter E, pyfrmai...@googlegroups.com
The errors are all machine zero as to be expected
Time = 0
Mesh DOFs = 400
Variable: U Error L1Norm = 8.49147e-17
Variable: U Error L2Norm = 1.76753e-16
Variable: U Error L1Norm = 8.49147e-17
Variable: U Error L2Norm = 1.76753e-16
Mesh DOFs = 1600
Variable: U Error L1Norm = 1.03079e-16
Variable: U Error L2Norm = 1.99849e-16
Mesh DOFs = 6400
Variable: U Error L1Norm = 1.02447e-16
Variable: U Error L2Norm = 1.98217e-16
Mesh DOFs = 25600
Variable: U Error L1Norm = 1.05134e-16
Variable: U Error L2Norm = 2.01533e-16
Variable: U Error L1Norm = 1.03079e-16
Variable: U Error L2Norm = 1.99849e-16
Mesh DOFs = 6400
Variable: U Error L1Norm = 1.02447e-16
Variable: U Error L2Norm = 1.98217e-16
Mesh DOFs = 25600
Variable: U Error L1Norm = 1.05134e-16
Variable: U Error L2Norm = 2.01533e-16
Reply all
Reply to author
Forward
0 new messages
