Skip to first unread message
Lyle Kopnicky
Sep 17, 2019, 8:08:47 PM9/17/19
to pdxfunc
Hi folks,
We're going through the MGS 2019 course on Lambda Calculus (http://www.duplavis.com/venanzio/mgs_lambda/index.html). For this meeting, please read the Lecture 3 slides and Chapter 5 of the draft book (linked from the above page).
Wednesday, September 25th, 2019, 6:30-8:30pm
Location:
Collective Agency
3050 SE Division, Suite 245 · Portland, OR
We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.
Location:
Collective Agency
3050 SE Division, Suite 245 · Portland, OR
We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.
Lyle Kopnicky
Sep 29, 2019, 11:16:59 PM9/29/19
to pdxfunc
Wow! We really got into some depth on these topics. We spent both a long discussing streaming data and anamorphisms, and then a long time discussing simply typed lambda calculus, especially previewing question #5 from the upcoming exercises.
%09%5Crightarrow%09C)

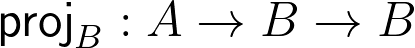
%09%5Crightarrow%09A)%09%5Crightarrow%09A)
%09%5Crightarrow%09B)%09%5Crightarrow%09B)
%09%5Crightarrow%09C)


%09%5Crightarrow%09D)%09%5Crightarrow%09D)
%09%5Crightarrow%09D)%09%5Crightarrow%09D)
Anamorphisms
I pointed out that the "anamorphism" discussed in the slides is really a particular anamorphism for streams, and is not the general definition of anamorphism. In general, an anamorphism (unfold) starts with a seed value and incrementally builds some sort of data structure through recursive application of a transition function. This could be a stream, or a tree, or any sort of data structure. This is the opposite of a catamorphism (fold), which takes a data structure and recursively breaks it down into a single value. It turns out that Wikipedia has a really nice explanation with some examples in Haskell: https://en.wikipedia.org/wiki/Anamorphism.
I showed a Haskell function ana from the Data.Fix library which is generalized to work for any sort of data structure. Unfortunately, that generalization makes it a bit more difficult to understand. You need to start with a special non-recursive version of the recursive data type you want to generate. Let's call that non-recursive version F. Then the recursive datatype you want to generate would be the greatest fixed point of F, denoted Fix F. To define an anamorphism, we need a function from a seed value to a value of type F; this is called an F-coalgebra.
In the case of infinite streams, the type F could be defined as:
data StreamF a = ConsF a b
Note how this is a small, finite data structure. It has only two values. The actual infinite stream type is
type Stream a = Fix (StreamF a)
This is like applying the Y combinator, but at the type level. To build a stream, one simply needs a function from some type b to the type StreamF a. You can think of the type b as the seed/state value. And type a represents the element value. So, let's say we want to write natsFrom, the function that produces natural numbers starting from an initial value. We can define it as:
natsFrom :: Nat -> Stream Nat
natsFrom n0 = ana (\n -> ConsF n (succ n)) n0
How does this correspond to what the slides said about anamorphisms? They said we needed to define two functions: an observation function f and a transition function t. Well, we have both here - they're just encoded slightly differently. Our observation function is just the identity function, and the transition function is the successor function. We've collapsed them into one function by using a datatype that lets us produce both results at once - the first value in the ConsF being the result of the observation function, and the second value in the ConsF being the result of the transition function.
By using this pattern, we can define anamorphisms for any singly-recursive data structure, not just streams.
Matt pointed out that infinite streams need to be constructed differently in ML. Due to the strict evaluation, they cannot be represented quite so compactly.
Simply Typed Lambda Calculus
We got a little confused about the base type "o" from the slides. The slides say there are "no closed terms" of that type. I'd seen other formulations of STLC where there were some primitive base types such as Nat or Bool. But here we have some abstract, apparently empty type. If there are no terms of type o, can there be terms of type  ? Well, the identity function,
? Well, the identity function, 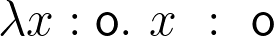 is such a term. But if there are no terms of type o, what would we ever substitute in for
is such a term. But if there are no terms of type o, what would we ever substitute in for  ? The book chapter makes no such claim that the type o has no closed terms.
? The book chapter makes no such claim that the type o has no closed terms.
Ed pointed out that the side condition 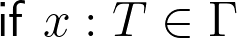 on the variable rule deriving
on the variable rule deriving 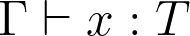 is a bit awkward and unnecessary. One could simply write the conclusion as
is a bit awkward and unnecessary. One could simply write the conclusion as  , mirroring the notation used in other rules.
, mirroring the notation used in other rules.
The slides mention weak normalization but do not define it. A weakly normalizing term is one there exists a finite reduction sequence that will lead to normal form. A strongly normalizing term is where any reduction order will lead to the normal form in a finite number of steps. In untyped lambda calculus, some terms are non-normalizing, some are weakly normalizing, and some are strongly normalizing. In STLC, all terms are strongly normalizing.
The chapter (5) also confused us a bit by showing us a language with Nat, Bool, if/then/else, and other constructs. We were trying to understand whether 'succ' in that context was a constructor, or a function. And was 'pred' another constructor? That question turned out to be meaningless, as we realized that this was not the lambda calculus, but just some arbitrary language being defined to show us how it could be typed.
Homework exercise 5
We skipped ahead to look at one of the exercise for next time: Exercise 5 from Exercise Set 3. It's a bit confusing. Matt had spent some time trying to define the pair type in terms of A, B, C, and the arrow operators. We came to the conclusion that it probably wasn't possible. However, I see the exercise as asking us instead to extend the grammar, so that 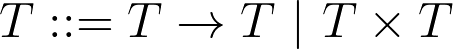 . The product type is not to be defined in terms of the other types, but taken as its own, primitive type constructor. Then you can use angle brackets to write values, thus:
. The product type is not to be defined in terms of the other types, but taken as its own, primitive type constructor. Then you can use angle brackets to write values, thus: 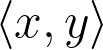 . Then you need to write the new typing rules for products.
. Then you need to write the new typing rules for products.
The reason we decided you can't implement pair/fst/snd using just arrow types is that the pairs must take either a selector of type  and return an
and return an 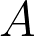 , or a selector of type
, or a selector of type 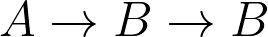 , and return a
, and return a  . But how can they do both? What type would you give to the pair?
. But how can they do both? What type would you give to the pair?
One thing that's confusing us a bit is the type variables. In STLC, there are no polymorphic types. So, a function can't have a type  , for example. The type variables are really a template for the sorts of functions we can construct. In the meeting insisted that the
, for example. The type variables are really a template for the sorts of functions we can construct. In the meeting insisted that the 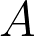 in one function's type was not the same as the
in one function's type was not the same as the 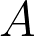 in another function's type. But I was wrong. They are the same because our type
in another function's type. But I was wrong. They are the same because our type 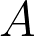 , however chosen, applies to all instances in the template - that is, the signatures of all the functions.
, however chosen, applies to all instances in the template - that is, the signatures of all the functions.
Let's look at the proposed types of the functions:
So, 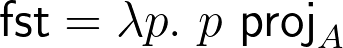 , and
, and 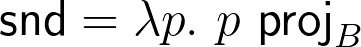 .
.
But then, for pair to work,  has to match both type
has to match both type 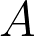 and type
and type  . It's not possible that they represent two distinct types.
. It's not possible that they represent two distinct types.
On the other hand, suppose we're using the polymorphic lambda calculus, where each function can have its own separately quantified variables. Then we can make it work:
Now when we apply a pair to fst, pair's type  will unify with
will unify with  's type
's type 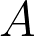 , which will also unify with type
, which will also unify with type  . When we apply a pair to snd, pair's type
. When we apply a pair to snd, pair's type  will unify with
will unify with  's type
's type  , which will also unify with type
, which will also unify with type  . The pair is polymorphic, with type
. The pair is polymorphic, with type %09%5Crightarrow%09C) , which lets it unify type
, which lets it unify type  with either type
with either type 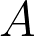 or type
or type  each time it is applied.
each time it is applied.
Hope to see you next time, when we'll go over all the exercises!
- Lyle
--
You received this message because you are subscribed to the Google Groups "pdxfunc" group.
To unsubscribe from this group and stop receiving emails from it, send an email to pdxfunc+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/pdxfunc/5e4e034b-2e0c-461c-8f09-0583c54f203f%40googlegroups.com.
Lyle Kopnicky
Sep 30, 2019, 11:42:50 PM9/30/19
to pdxfunc
I suppose the correct symbol for quantifying over the types in the polymorphic lambda calculus (aka higher-order lambda calculus, system F, or  ) is
) is  , not
, not  . But it conveys the same idea. So, e.g., for pair, the type would be:
. But it conveys the same idea. So, e.g., for pair, the type would be:
%09%5Crightarrow%09C)
%09%5Crightarrow%09%5Cgamma)
Alternately, depending on the exact syntax, you might see the pis collapsed into one, or Greek lowercase letters used for the type variables, or a colon and star following each type variable to show that they are of the kind of types:
...we'll get to System F at the end of the course.
Reply all
Reply to author
Forward
0 new messages
