Theory meeting, 7/10/19 - Lambda Calculus

[Lyle Kopnicky]

Hi folks!

Back from a hiatus of a few months, we're ready to start on some new material. I've chosen a short course on lambda calculus from the Midlands Graduate School 2019, which I attended back in April. (Though I only attended the first lecture of the lambda calculus course, I found it very well-designed.) There will be a bit of type theory in it as well.

The course outline is at http://www.duplavis.com/venanzio/mgs_lambda/index.html. We will be going over the first set of lecture slides in the meeting. There are no assignments for this first meeting.

Wednesday, July 10th, 2018, 6:30-8:30pm

Location:
Collective Agency

3050 SE Division, Suite 245 · Portland, OR

We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.


RSVP at: https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/bzvndryzkbnb/

[Lyle Kopnicky]

We're off to a good start! We went over the first set of slides in the meeting, and everyone had ideas to contribute.

One of the things we wondered about was why exponentiation of Church-encoded numerals can be done just by applying the exponent to the base, as a function. Working through an example helped:

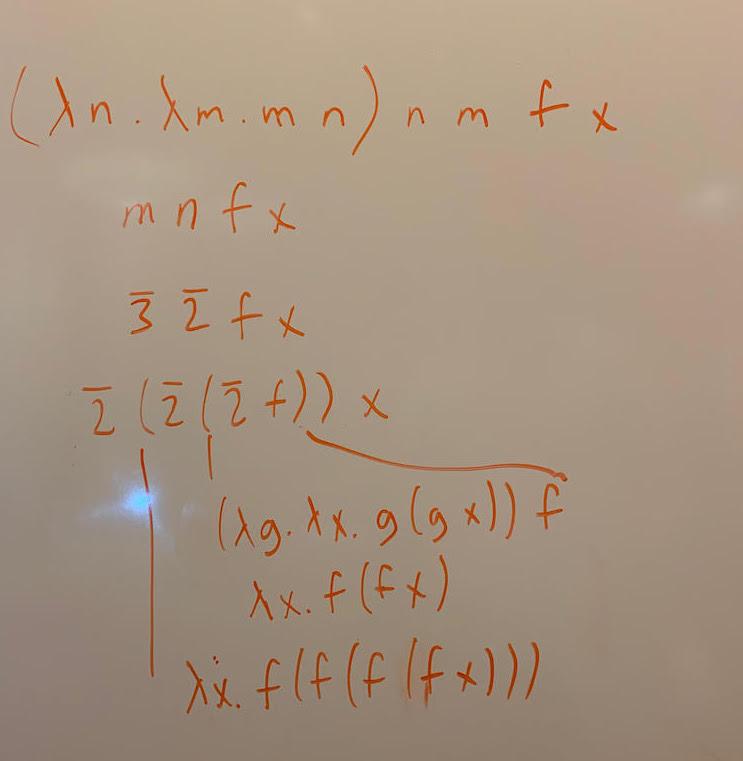
One of the questions we were left with was this: Supposedly the point of Church-encoding data is so that you can do computations with it. But when you get your result, how can you interpret it? We are not guaranteed that the lambda expression will reduce to a normal form (as opposed to continuing infinitely). If it does converge to an irreducible expression, how do we know whether that expression is equivalent to a particular Church numeral? In general it's undecidable whether two lambda expressions are equivalent.

Perry said that Mayer Goldberg had produced a program that could interpret lambda calculus results, that is, "decode" the Church encoding. I'd be interested to see that. I'm sure there would be edge cases where it wouldn't work, but perhaps it works most of the time. Interestingly, Goldberg also wrote a paper showing that any equality predicate on Church numerals could be circumvented - that is, we can construct a term that satisfies the equality test with all Church numerals.