Theory meeting, Sept. 26th

[Lyle Kopnicky]

We'll discuss Chapter 15, "Functions", of Logic and Proof (https://leanprover.github.io/logic_and_proof). Please try to work the exercises beforehand. At the meeting anyone will be able to present and contribute to the discussion.

September 12th, 2018, 6:30-8:30pm

Location:

Collective Agency

3050 SE Division, Suite 245 · Portland, OR

We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.

RSVP at:

https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/254874972/

[Lyle Kopnicky]

I should have said September 26th (today) in the body of the message, as in the subject.

[Matt Rice]

unfortunately something has come up and i am not going to be able to
make it this week, apologies for the last minute notice.

besides that, I should say i had some difficulty figuring out the
correct nominal evaluation of the set model,
I also struggled with inverse functions on the ring of integers, (In
particular the proof involving inverse functions being unique for the
function(s) f(x) = x * -1, f(x) = x, and f(x) = x * 1, which seemed to
extend to the identity function and its inverse(s) outside of rings,
thwarting my attempts at the exercises)
so none of my notes actually managed to overlap with the chapter.

> --
> You received this message because you are subscribed to the Google Groups "pdxfunc" group.
> To unsubscribe from this group and stop receiving emails from it, send an email to pdxfunc+u...@googlegroups.com.
> To post to this group, send email to pdx...@googlegroups.com.
> Visit this group at https://groups.google.com/group/pdxfunc.
> For more options, visit https://groups.google.com/d/optout.

[Lyle Kopnicky]

No worries, Matt. We had a good discussion, but will continue reviewing the Chapter 15 exercises this Wednesday.

To which exercise are you specifically referring, that you struggled with?

[Lyle Kopnicky]

We had a great meeting. We went over the chapter, and looked at some of the exercises (exp. #1), but didn't go through all of them. We'll continue with the exercises next time.

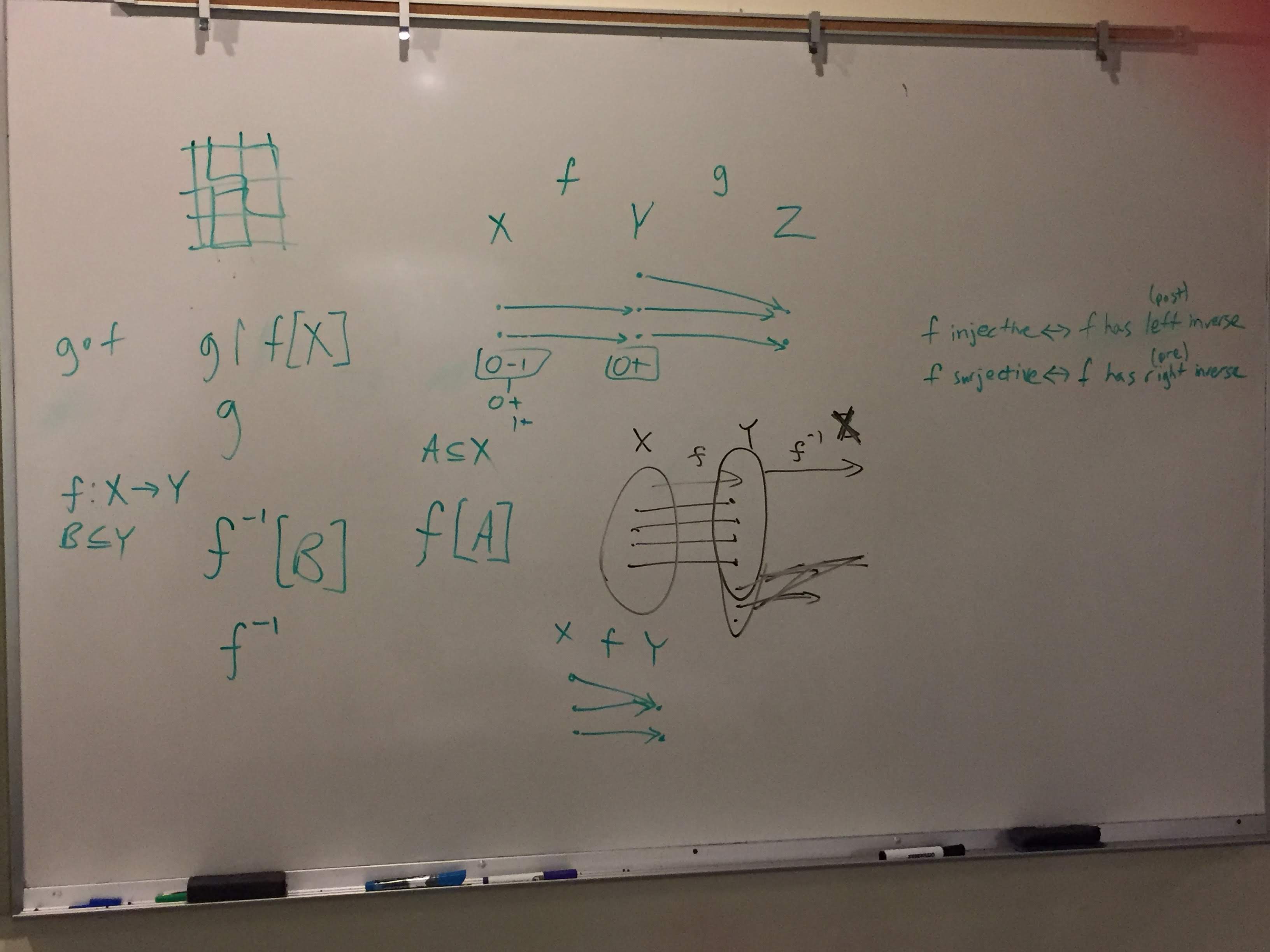
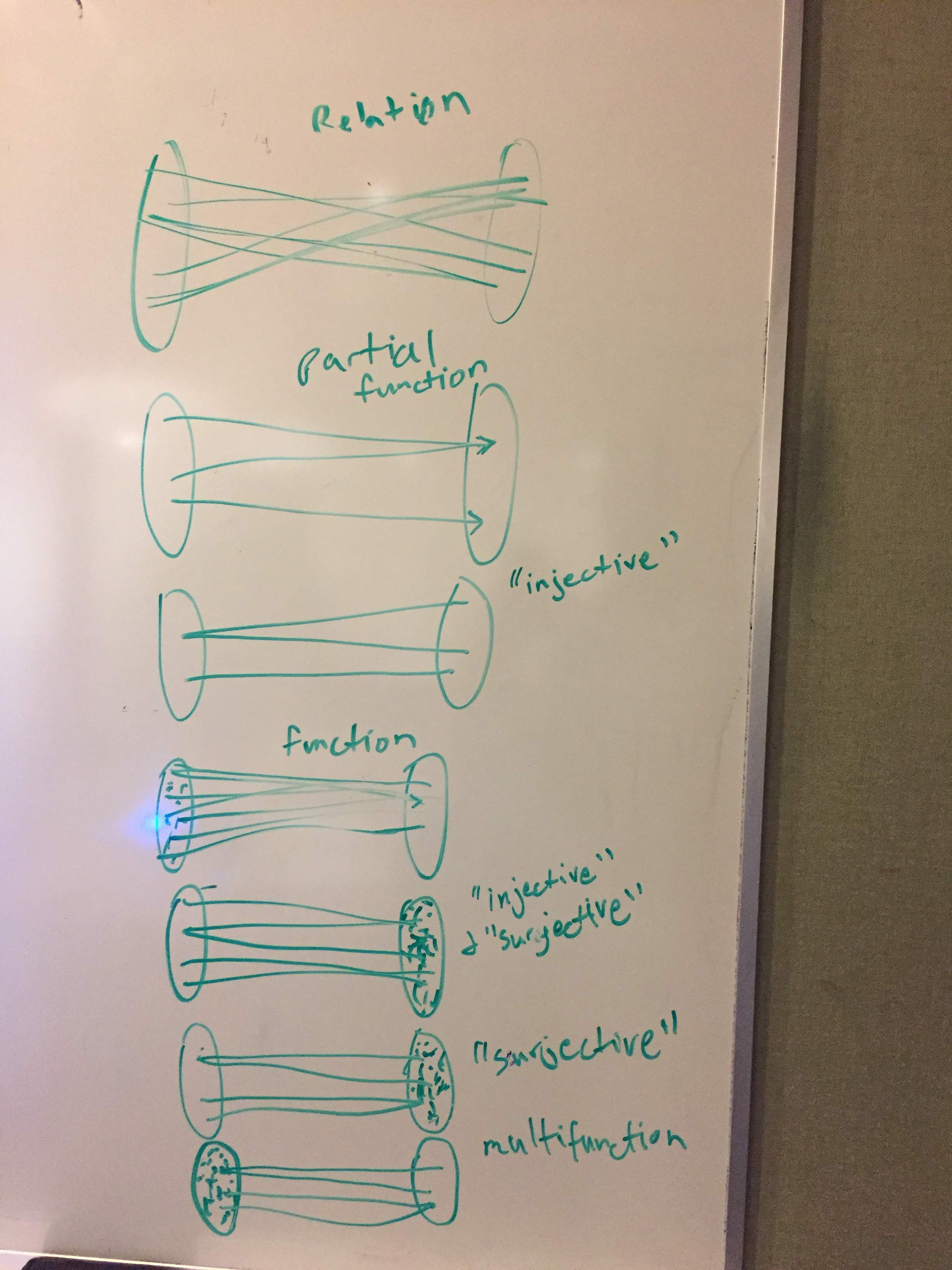
I explained a lot about the kinds of binary relations, how they are classified as functions, multifunctions, injective, surjective. It's a little confusing how the terms relate. Injective and surjective don't seem to be opposites, yet somehow they are complementary. Imagine the domain of a function on the left, and the codomain on the right. Then "Injective" means that for every value on the left, it maps to a unique value on the right. "Surjective" means that for every value on the right, there's at least one value on the left that maps to it. To me these seemed like arbitrarily chosen properties, not quite opposites of each other.

But reading through the chapter, I noticed a powerful relationship: If has a left inverse, then it is injective. If has a right inverse, then it is surjective. Wow. Clearly, left and right inverses are opposites of each other. So this gives a clearer hint as to the relationship between injectivity and surjectivity. Also, if  is surjective, then it has a right inverse. If  is injective, it has a left inverse, right? Well, not quite. Only if the domain is nonempty. That doesn't seem to restrictive.

Here are some diagrams I drew relating to these concepts. I also talked some seemingly ambiguous notation, . Does that mean the preimage of , or the inverse of applied to ? It turns out if both exist, they will be the same, thus removing the ambiguity.

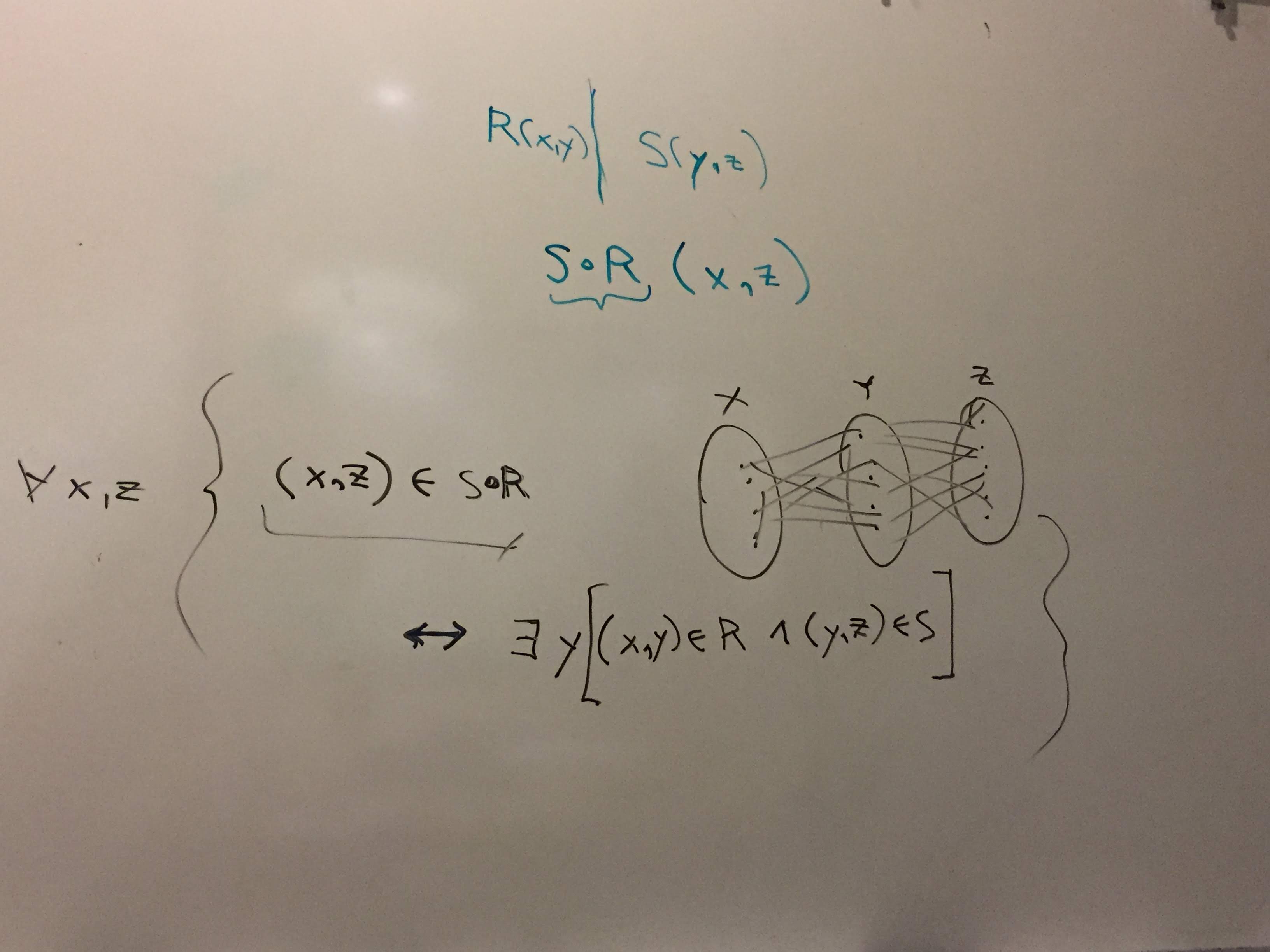
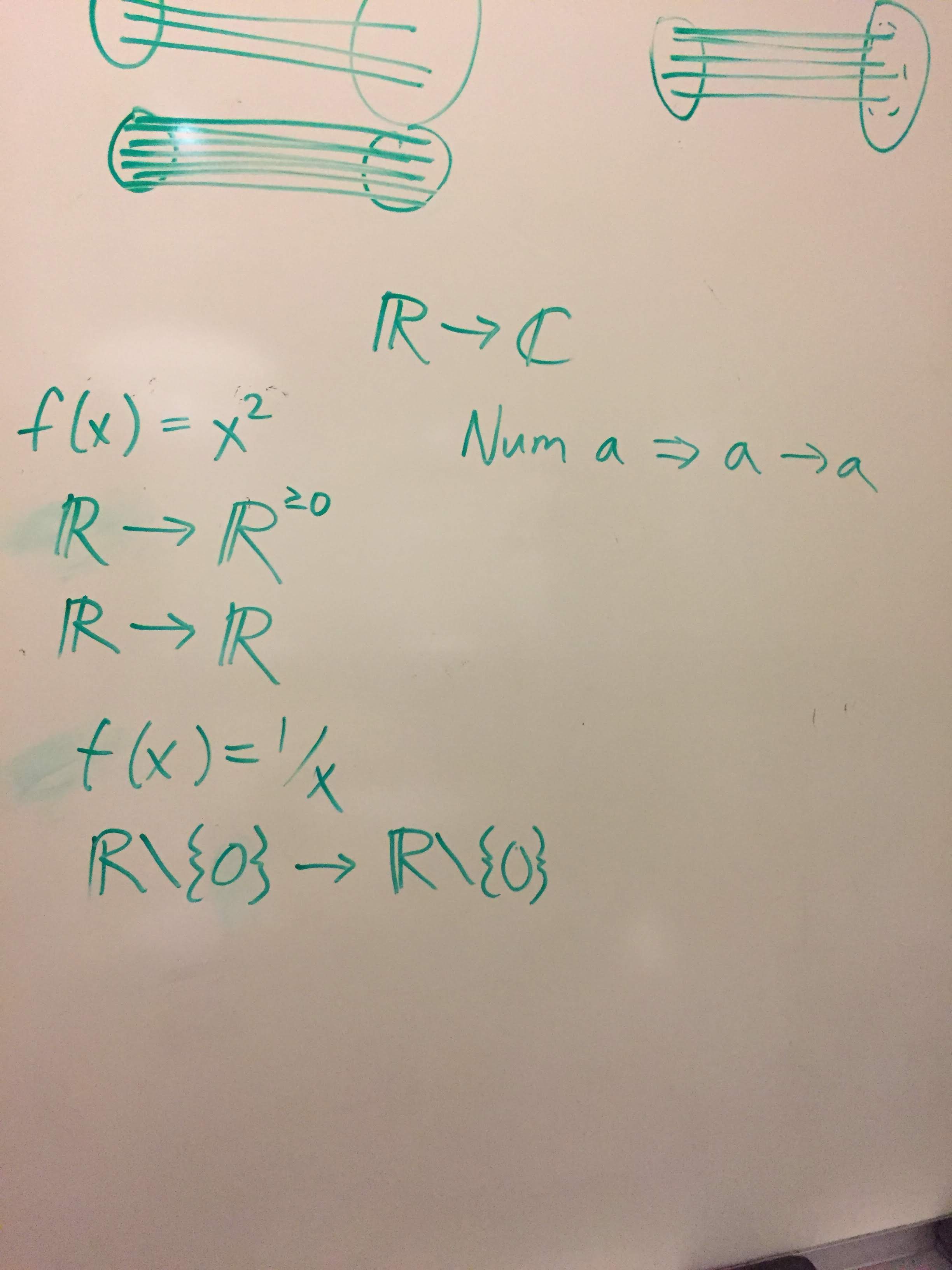
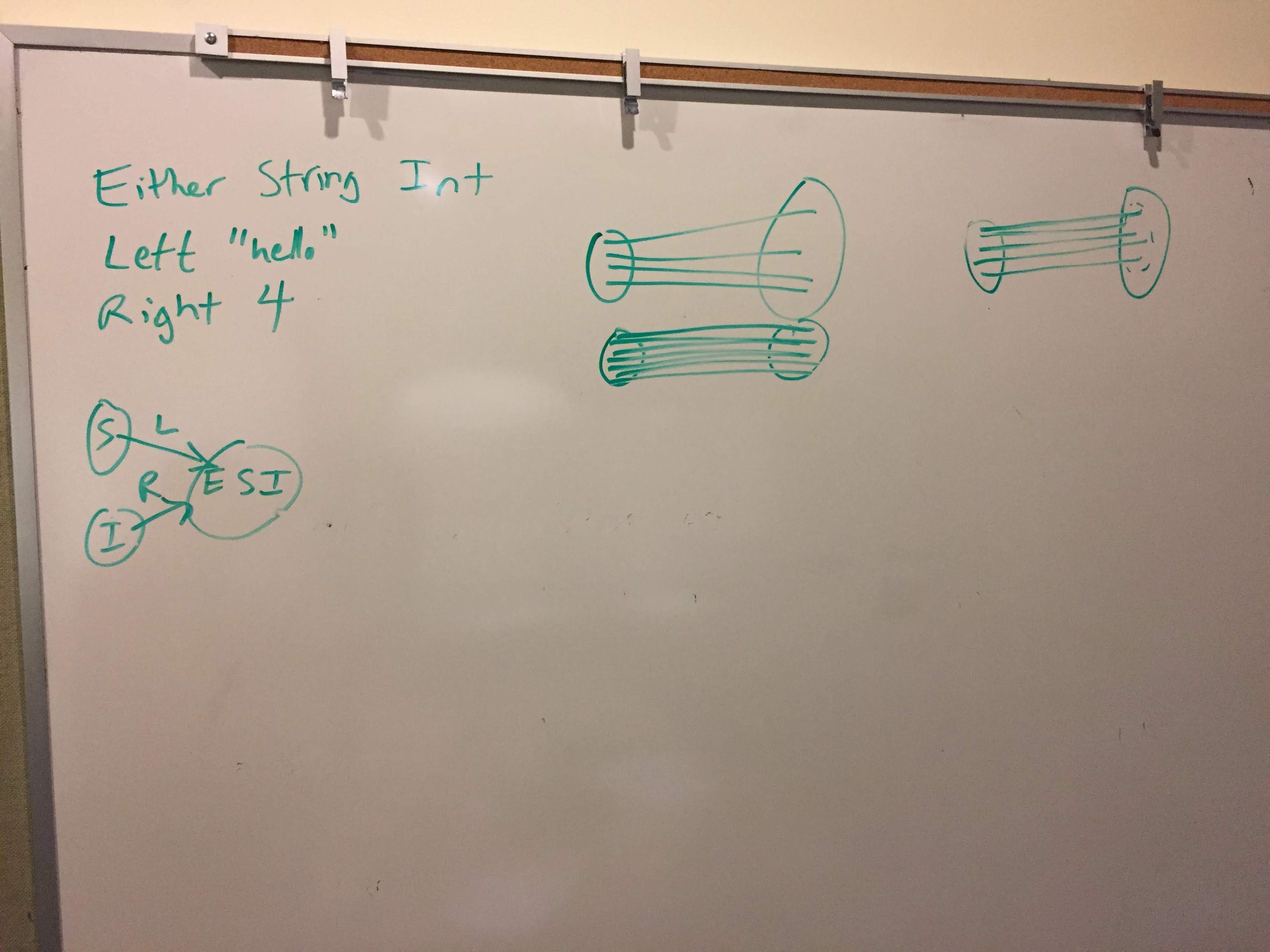
Then Ed sketched out a solution to Exercise 6, defining composition for binary relations, with some guidance from me:

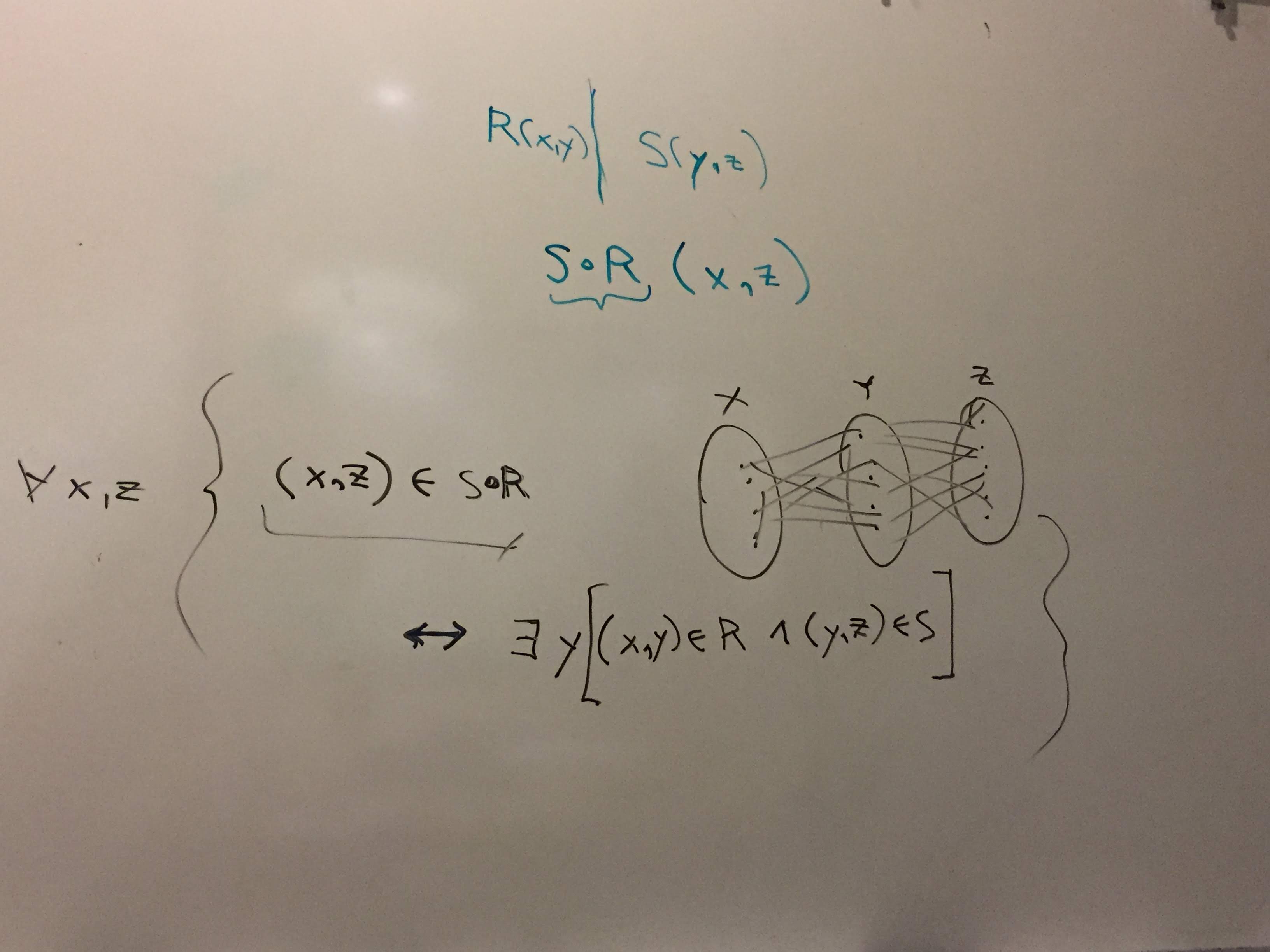
I talked about the important distinction between the codomain and range of a function. The codomain is definitional, and fits well with type theory. One can define the function to be over , and then say its definition is . Well, clearly all values produced will be nonnegative, but that isn't reflected in the type (domain/codomain). So the function is not surjective. One could alternately define it with a codomain of , that is, nonnegative real numbers, and then it would be surjective.

The same goes for defining the domain, and then calling something a partial function over that domain. These are important distinctions, that are not often drawn in math texts.

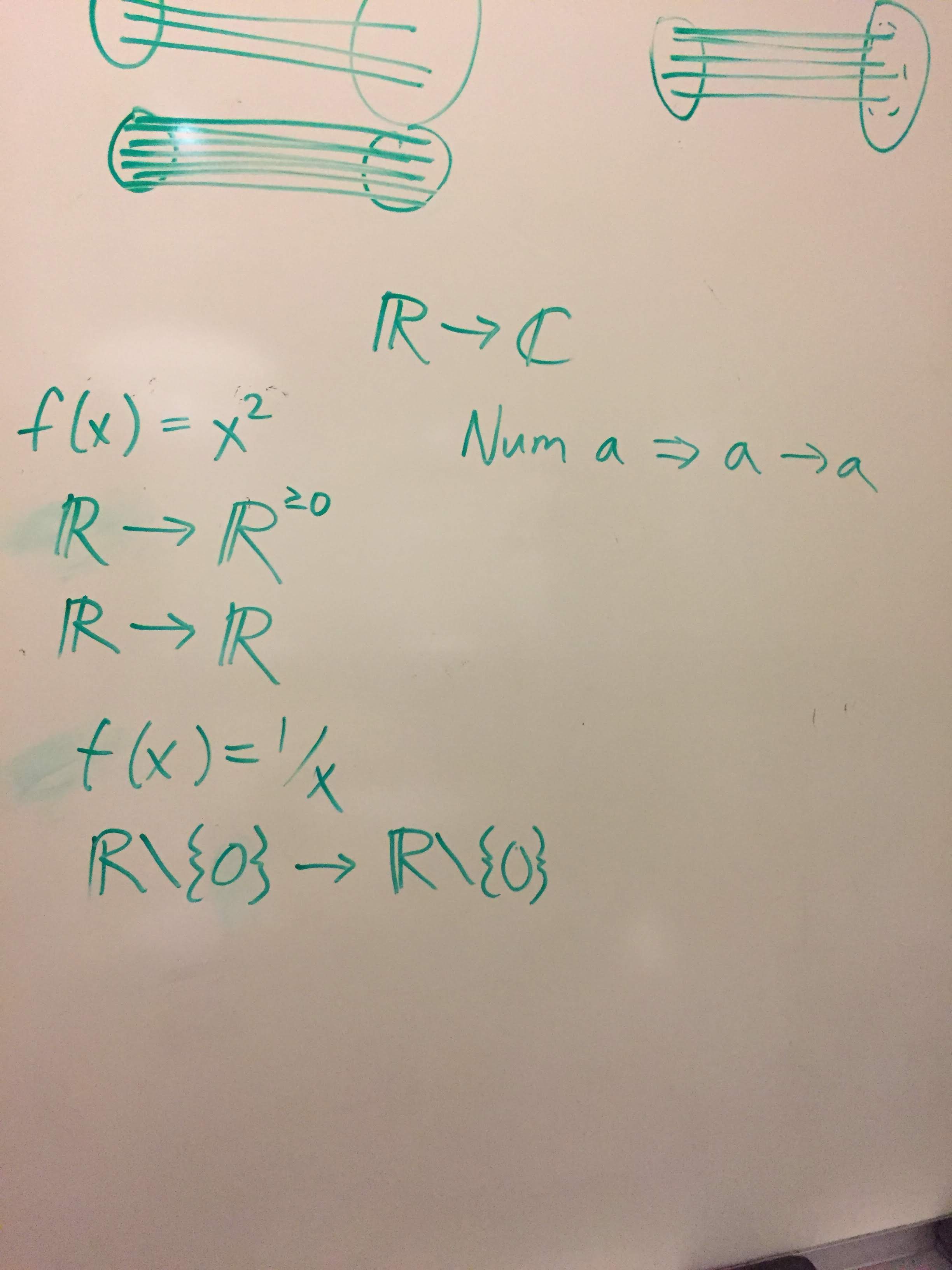
Here I explained an intuition for the notion of injectivity. My first thought was of an inkjet printer, "injecting" ink into paper, and how the ink would expand after it came out of the nozzle, almost as if the particles were repelling each other, and thus keeping them distinct at the target. But, it's a relatively weak intuition for the name.

My other intuition comes from algebraic data types, where we speak of a sum type having multiple "injection" functions. E.g., we have the String type and the Int type, and we can produce a type that can be either a String or an Int, called Either String Int. Then the injection functions are called Left and Right. It's like the two other types are being "injected" directly into the sum type, in such a way that they stay separated.

The key intuition with injection is that it means it is reversible. If you map "hello" to Left "hello", you can get back to "hello". If you map 4 to Right 4, then you can get back to 4.

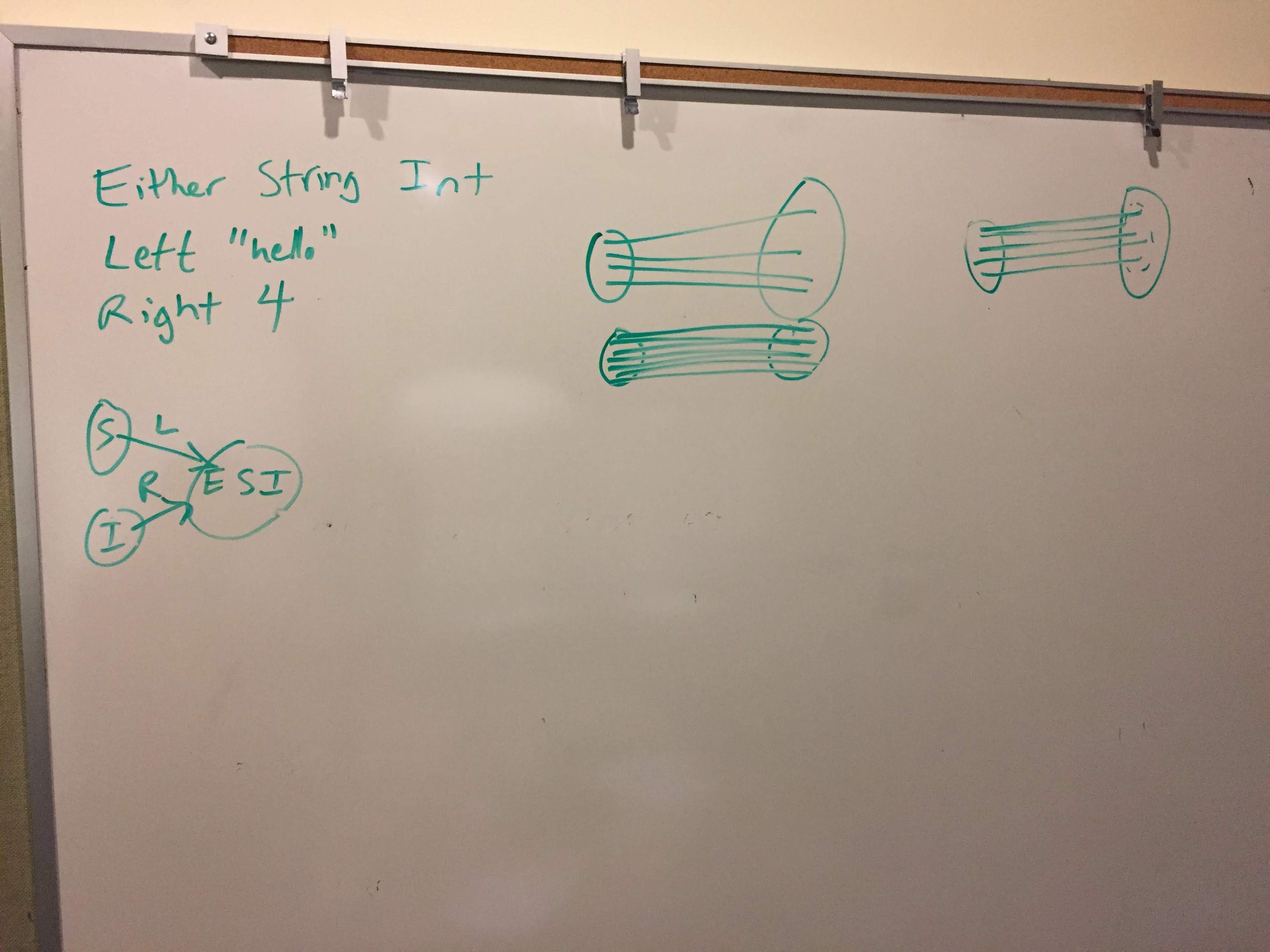
Finally, I was searching for a more consistent, symmetrical way of classifying binary relations. I started thinking about it in terms of the cardinality of lines that could be attached to a point on either side. For example, a function must have exactly one line connected to each point on the left. An injective function must also have zero or one lines connected to each point on the right. So one can separate the notion of injectivity from functions. We can have an "injective" relation (I use scare quotes because the term is not normally used with non-functions), that has zero or one lines connected to each point on the right, but may have any number of lines connected per point on the left.

Then one can see some symmetry. One can talk about the inverse relation that swaps the left and right sides. Every total functional relation then has an inverse relation which is "injective" and "surjective". Every partial function has an inverse relation which is "surjective". So surjectivity is the dual of totality. And injectivity is the dual of being (partially) functional.

This explains why surjective, total functions have a right inverse. First of all remember that a right inverse is applied before the function. I.e., for all in the codomain of ,  if and only if 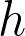is right inverse to . I like to call it a "preinverse". The surjectivity of  is exactly what is needed for 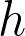to be total.

It also explains why injective, total functions have a left inverse. I like to call the left inverse a "postinverse" because it is applied after the function. I.e., for all in the domain of ,  if and only if is left inverse to . The injectivity of is exactly what is needed for  to be a function.

I'd like to develop these ideas further, but I realize that if I keep revising this, I'll never send it out, so I hope you find this helpful.

- Lyle

[Ed Snow]

At the last meeting I rashly volunteered to write up something for exercise 15.5. The intended result is a proof that would convince a human mathematician, but I thought I would give Lean a try. I've gotten reasonably close, and the result can be found at:

https://gist.github.com/es30/e6117c5fdab84b7213f3ce37082a74b8

There are a number of sorrys to be filled in. They are commented and represent reasonably straightforward jumps left in the interest of time. My one frustration has been in constructing a definition of image_of_f that Lean finds acceptable. I'lll wrestle with this further prior to the meeting.

-Ed

[Lyle Kopnicky]

Great, thanks, Ed! I'm looking forward to going over your solution tonight.

--

[Ed Snow]

For the sake of completeness, I've finished off the solution to exercise 15.5 in Lean (sorry-free this time) using the machinery introduced in chapter 16:
https://gist.github.com/es30/9158e80cb4b547c7a04893e51acbeff1
(second file in the gist)

The first file in the gist is my attempt at the second part of exercise 15.3, which was a subject of discussion at the last meeting. It contains two sorrys representing straightforward logical steps. The first is due to my running out of time, the second results from my failure to come to grips with Lean's finnicky eq.subst mechanics.

See you all at the meeting.

- Ed