Theory meeting, Aug. 22nd

[Lyle Kopnicky]

We'll discuss Chapter 13, "Relations", of Logic and Proof (https://leanprover.github.io/logic_and_proof). Please try to work the exercises beforehand. At the meeting anyone will be able to present and contribute to the discussion.

August 22nd, 2018, 6:30-8:30pm

Location:

Collective Agency

3050 SE Division, Suite 245 · Portland, OR

We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.

RSVP at:

https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/mpwwbqyxlbdc/

[Lyle Kopnicky]

Great meeting tonight! We shared our work on the Chapter 13 exercises, as well as some insights related to the chapter itself.

One thing we discussed is that while we get substitutability with equality, we don't get it for equivalence. For example, we may define an equivalence relation on natural numbers such that all even numbers are equivalent, and all odd numbers are equivalent. But this doesn't mean that if is equivalent to (that is, they are both odd, or both even), that we can substitute one for the other in any logical formula. For example, is satisfiable, but is not satisfiable. The problem is that the equivalence relation has nothing to do with our formula.

We drew directed graphs and talked about which ones would or would not represent various kinds of orders. We simplified the graphs to Hasse diagrams by eliminating self arrows and transitive arrows, assuming reflexivity and transitivity. A preorder can have cycles, but a partial order cannot. A partial order is analogous to a directed acyclic graph (DAG). A total order must be linear. I mentioned that in category theory, every category with at most one arrow between each object is a preorder, since reflexivity and transitivity are built-in requirements.

I also explained how a partial order could be generated from any preorder, by dividing the elements into equivalence classes, such that  when  and . That is, when 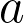and are in a cycle with each other. Also all arrows from any element in the equivalence class to any element in some other equivalence class must be collapsed into a single arrow. We talked about how a minimum element is not necessarily unique in a preorder, but must be in a partial order, and that all the minimum elements in that preorder fall into an equivalence class.

Ed pointed out although exercise 6 asks us to show that the relation of parallel lines is an equivalence relation, Wikipedia specifically stated that it isn't! (According to Euclid's definition.) For it to work, you have to use a definition of parallel that allows a line to be parallel to itself. We decided the important thing in that exercise was the intuition of the solution, rather than a rigorous proof, as we are not studying geometry.

We talked about how homotopy type theory is based on the principle that "equivalence is equivalent to equality", which means that we can simplify proofs by only proving things about equivalence classes rather than individual elements.

I gave a taste of lattice theory, talking about meets and joins on the lattice of divisibility, and how I attempted to extend this to a Heyting algebra, but failed, only to be told by a brilliant Ph.D. student how it could be done instead with a lattice of "ideals of the integers". I don't recall all the details of that, but maybe sometime I could put together a presentation.

Next time, we'll discuss Chapter 14, on "Relations in Lean".

- Lyle