Skip to first unread message
Lyle Kopnicky
Nov 24, 2019, 10:58:04 PM11/24/19
to pdxfunc
Hi folks,
We're going through the MGS 2019 course on Lambda Calculus (http://www.duplavis.com/venanzio/mgs_lambda/index.html). In this meeting, we'll review Chapters 6 and 7 of the draft book (linked from the above page), and Exercise Sheet 4.
Wednesday, December 11th, 2019, 6:30-8:30pm
Location:
Collective Agency
3050 SE Division, Suite 245 · Portland, OR
We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.
RSVP at: https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/vnpwfryzqbpb/
We're going through the MGS 2019 course on Lambda Calculus (http://www.duplavis.com/venanzio/mgs_lambda/index.html). In this meeting, we'll review Chapters 6 and 7 of the draft book (linked from the above page), and Exercise Sheet 4.
Wednesday, December 11th, 2019, 6:30-8:30pm
Location:
Collective Agency
3050 SE Division, Suite 245 · Portland, OR
We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.
RSVP at: https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/vnpwfryzqbpb/
Lyle Kopnicky
Dec 15, 2019, 8:47:33 PM12/15/19
to pdxfunc
Another interesting discussion. We decided to start by going through the book chapters (6 and 7) before getting to the exercises. We got through Chapter 6 and most of Chapter 7, but didn't get to the section on coinductive types.

%09%5Cleadsto%09h%5C%09n%5C%09(%5Cmathsf%7Brec%7D%5FT%5C%09h%5C%09a%5C%09n)) So for the base case of 0, we just return the value
So for the base case of 0, we just return the value 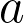 .
.
I think we all got a better understanding of System T, and how  works, by using a function that computes one step of the solution and applies it to the solution for the next smaller value of
works, by using a function that computes one step of the solution and applies it to the solution for the next smaller value of  .
.
The reduction rules are:
For the recursive case of  , we compute the result for
, we compute the result for  and then apply
and then apply 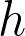 once to it. Thus the
once to it. Thus the 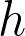 function will ultimately get applied
function will ultimately get applied  times.
times.
We can look at this like mathematical induction, where in the inductive step we have an inductive hypothesis of  and need to prove
and need to prove ) . Or we can look at the second argument to
. Or we can look at the second argument to 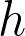 as being an accumulator, containing the accumulated result of computation on the smaller problem.
as being an accumulator, containing the accumulated result of computation on the smaller problem.
We even got a pretty good intuition as to how the Ackermann function can be rewritten as as doubly-nested calls to  . Because System T is total, this shows that Ackermann's function must terminate.
. Because System T is total, this shows that Ackermann's function must terminate.
We talked about adding primitive booleans, products, and sums to System T. We showed how lists can be built in this way, and how they can be folded using 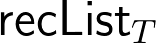 .
.
Then we generalized over products and sums, unifying inductive data types into a common pattern. The combination of products and sums in a data type can be generalized into the idea of a strictly postitive functor. This functor  is like "one step" of the datatype, so we can compute the full inductive datatype by using the fixpoint operator
is like "one step" of the datatype, so we can compute the full inductive datatype by using the fixpoint operator 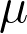 . We can generalize all
. We can generalize all  functions for different data types into a function called
functions for different data types into a function called 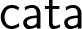 . And we can generalize the
. And we can generalize the 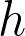 function that we supplied to
function that we supplied to  to something called an
to something called an  , which is just a type
, which is just a type  and a function from
and a function from  .
.
We also talked a bit about category theory, and what functors look like there, and their laws.
We talked about bit streams, and how they must be generated step-by-step. The bit stream itself is already in a normal form. Then we can apply a selector to get the first bit or the rest of the stream, and that's when the computation takes place. At any point in time, the stream really only holds a current state.
This is true for any kind of coinductive type: There's a state, and further states can be produced by selectors. In a coinductive binary tree, there's a single state, and selecting the left branch advances the state in one way, but selecting the right branch advances the state in a different way. We also represent the state with a type  , and that's no coincidence. The state when building a coinductive type is very much like the accumulator when folding an inductive type, but the process is happening in reverse.
, and that's no coincidence. The state when building a coinductive type is very much like the accumulator when folding an inductive type, but the process is happening in reverse.
We didn't have time to go over the exercises, but Ed pointed out that Exercises 2 and 3 are already solved in the text. Nobody understands what Exercise 4 is asking for. I'll keep thinking about it.
We'll talk about how to generalize coinductive types next time, and go over the exercises. Happy Holidays!
- Lyle
--
You received this message because you are subscribed to the Google Groups "pdxfunc" group.
To unsubscribe from this group and stop receiving emails from it, send an email to pdxfunc+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/pdxfunc/f9aa7d63-d251-41e7-ba54-a220c39c7481%40googlegroups.com.
Reply all
Reply to author
Forward
0 new messages
