Skip to first unread message
Lyle Kopnicky
Jan 18, 2020, 4:07:30 PM1/18/20
to pdxfunc
Hi folks,
Wednesday, January 22nd, 2020, 6:30-8:30pm
Location:
Collective Agency
3050 SE Division, Suite 245 · Portland, OR
We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.
RSVP at: https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/qjvbnrybccbdc/
We're going through the MGS 2019 course on Lambda Calculus (http://www.duplavis.com/venanzio/mgs_lambda/index.html). For this meeting, please read the section of Chapter 7 about coinductive types, and try Exercise 4 from Exercise Sheet 4 of the material linked from the above page.
Location:
Collective Agency
3050 SE Division, Suite 245 · Portland, OR
We'll be in the second floor conference room, not in the Collective Agency suite. It's just off the lobby area in the middle of the second floor. Elevator access is available.
RSVP at: https://www.meetup.com/Portland-Functional-Programming-Study-Group/events/qjvbnrybccbdc/
Lyle Kopnicky
Mar 1, 2020, 8:01:02 PM3/1/20
to pdxfunc
We discussed the type in Exercise 4 from Exercise Sheet 4: 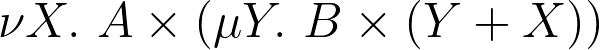)) . The idea is that
. The idea is that  and
and 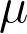 are being used as binding forms with built-in fixed points.
are being used as binding forms with built-in fixed points.
To understand this, first look at the inner expression ) . This defines a functor
. This defines a functor ) . Since
. Since  is free, it can be seen as a fixed type. Note that it's a strictly positive functor, since there are no function arrows to the left of
is free, it can be seen as a fixed type. Note that it's a strictly positive functor, since there are no function arrows to the left of  . The entire expression is then computing the fixed point
. The entire expression is then computing the fixed point  , an inductive data type.
, an inductive data type.
The outer  binding can be understood in a similar way. It defines the functor
binding can be understood in a similar way. It defines the functor 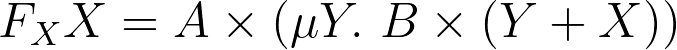)) , which is equal to
, which is equal to 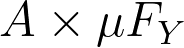 . This is also a strictly positive functor, since there are no function arrows to the left of
. This is also a strictly positive functor, since there are no function arrows to the left of  . The entire expression computes the fixed point
. The entire expression computes the fixed point  , a coinductive data type.
, a coinductive data type.
The full data type then works out to an 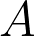 followed by one or more
followed by one or more  s, then another
s, then another 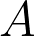 , one or more
, one or more  s, and so on to infinity. We weren't quite sure what this could be used for, except perhaps an infinite stream of data with periodic checksums.
s, and so on to infinity. We weren't quite sure what this could be used for, except perhaps an infinite stream of data with periodic checksums.
A right fold can truly short-circuit. You can give it an infinite list, and, proceeding from the left, if it finds a value that causes it to short-circuit, it will.
A left fold must first do a pass over the entire list. Thus it cannot handle infinite lists. It then does a second pass which can short-circuit, in the sense that it will only perform its operation for values to the right of the short-circuiting value. If the calculation it performs is expensive, but traversing the list is quick, then this could be effective as a short-circuit, since it can save a lot of work.
Here's my code sample, defining foldl and foldr (in a lazy way), and comments showing the expansion of short-circuiting calls: https://gist.github.com/lylek/1e289dcba6455747797502a82408e852. I used https://gist.github.com/CMCDragonkai/81e2b81ddf0c4901ca67 and http://crypto.stanford.edu/~blynn/haskell/warts.html as references.
These are both lazy folds. Note that a strict left fold cannot short-circuit at all.
- Lyle
--
You received this message because you are subscribed to the Google Groups "pdxfunc" group.
To unsubscribe from this group and stop receiving emails from it, send an email to pdxfunc+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/pdxfunc/0d06b629-d694-4c0f-b034-34e7d52bb62d%40googlegroups.com.
Reply all
Reply to author
Forward
0 new messages
