Comprehensive Mode Naming System

[iClifDotMe]

I have developed a method for naming all possible 12-TET modes using a 3-digit code that is rich-encoded, human and machine readable, and can be quickly mathematically manipulated to derive the intervals / pitch classes associated with a particular mode. The method solves the issues surrounding the use of traditional mode names in many ways. First, there is one and only one name for a given mode, which deals with the issue of modes with multiple common names or no common name. Second, the ability to derive the intervals / notes from the code mathematically removes the need for memorization (human) and database storage (machine) of that data. The method also simplifies operations involving things like randomization, modal transposition, etc.

I am looking for app developers who might be interested in integrating this system internally and/or externally (user-facing) in their apps. Internal examples might range from simple storage methods / optimization to mathematical modal transposition (e.g. translating a melody from A Minor to A Hungarian Major). Examples of external uses might be allowing a user to define a scale quickly by entering a 3-digit code, creating notation using the code as an alternate to traditional key signatures, or simply exposing the codes along with or in leiu of common scale names. There is also potential for a reference / calculator utility for users to quickly translate codes to scales/modes and vice versa, providing the notes, approximate traditional key sigs, etc.

My goal is to patent and publish this method for wider use within the general music community to aid in composition and analysis. Frankly, I think I've developed a unique method that will be of value to composers, music theorists, instrumentalists and programmers - and I'd like to receive credit for my work and maybe even make a little money from it. But for now, I'd like to find some folks willing to help explore and prove the method. Feel free to reply here, but please also contact me directly at iC...@me.com if you are interested in discussing further.

Thanks, and thanks for all you do! :)
Clif (@iClifDotMe)

[rob.fi...@gmail.com]

I probably ended up writing code almost exactly like yours when writing a Samchillian variant (at least three rewrites of it), because you really are stuck with a 7-note system in which efficiently moving through adjacent modes and scale shapes is important. 

 

The first thing is that when you mean “modes” to mean all the various diatonic scale shapes, then you are on to a pretty obvious idea with a lot of precedents.  ie: start with some arbitrary “mode” like minor and add/subtract a sharp in circle of fifths order, and it gives you all of the 7 diatonic mode shapes, then one or two other parameters lets you capture melodic minor-type shapes, and the whole tone and diminished shapes.  Then you can add further parameters by being able to swap out the scale shape for another.

 

http://github.com/rfielding/Xstrument

 

So, you can generate all the well-known scale shapes from a very small system with a minimum number of parameters.  Ultimately, this is possible because the scale systems in use have a basis in physics:   you start from a base tone, and go out +/- 2 fifths (or fourths...same result) and you have a pentatonic scale.  you can use 12-TET fourths to get a pentatonic you know from the piano, or use Just Intervals to get Pythagorean pentatonics.  If you stretch out 1 more tone in each direction, you go +/-3 fifths to get the diatonic scales, from where the zoo of 7 modes you usually use come from (dorian, minor, major, etc).  Again, if you use 12-ET intervals then you get a diatonic scale like on piano, but if you use physical fifths, then you get a just intonation diatonic scale.  If you stretch out +/-6 fifths, then you end up with a 12-note chromatic scale.  If you use 12-ET then it wraps around to give you the 12 note system you are so used to.  If you use Just fifths, then you get wolf-tone where things sound incredible as long as you are careful about how you transpose.  If you use Just fifths, then you actually should go out some more until you have duplicates of the sharps and flats; which gives you the piano layout of some ancient organs that need 17-notes per octave because each black key had to be split in half to have Just tuning without wolf tones.

 

So far, this is just a simple exercise with 1 parameter (how many fifths from the root) that generates: pentatonics in every 5-note mode, diatonics in every 7 note mode, the chromatics.  It’s a simple matter to substitute the underlying diatonic shapes for other common ones, like minor with sharp 7, minor sharp 6 and 7, .. which is one step from being a major scale with sharp 3, 6,7.  (ie: so navigating not just the circle of fifths, but a pathway from minor to major). 

 

The underlying code to do this is indeed beautiful; which is why so many people have run into it already.  It’s like running into Pascal’s triangle for the first time when you are doing something that you thought had nothing to do with it.

 

You need to be talking to the Microtonal Facebook group.  Even if you don’t use microtonalism, these guys know (way too much for their own good) about how to make small systems to encode and generate scale spaces.  And read up about Erv Wilson’s “Moments of Symmetry”, which manages to capture almost all known scales in a single system where you usually just use 1 parameter.

 

 

 

Sent from Windows Mail

--
You received this message because you are subscribed to the Google Groups "Open Music App Collaboration" group.
To unsubscribe from this group and stop receiving emails from it, send an email to open-music-app-colla...@googlegroups.com.
For more options, visit https://groups.google.com/groups/opt_out.

[nlogmusic (TempoRubato - NLogSynth)]

Hi Clif,

thanks for your contribution to this. Just a short reminder: This group was founded to be as open as open can be. From the early on we said, that all topics published and discussed here shall be as free of proprietary intellectual property like patens etc. as it can be. Nothing against patents by itself, but this space is not for discussing anything which is already or is intended to be in the future as a patent. The information here shall be available to everybody fur use and advantage without any licensing or whatever.

I just want to avoid any misunderstandings which may lead later to problems we can avoid.

Best

Rolf

[iClifDotMe]

Sorry for the delay in replying, but apparently I don't have my notifications set up correctly. What you are saying makes perfect sense, and I will reconsider the way I am presenting my ideas. Thanks :)

[iClifDotMe]

Thanks for your thoughtful reply, Rob. You've given me plenty of resources to delve into.

I realized after reading your reply and re-reading my post that I was unpurposefully vague in my description. I think the value of my approach is in its simplicity and human readability. There are a few math tricks, but nothing near as complex and robust as the methods you mention.

Here is an excerpt from a post I made on the system in layman's terms:

---
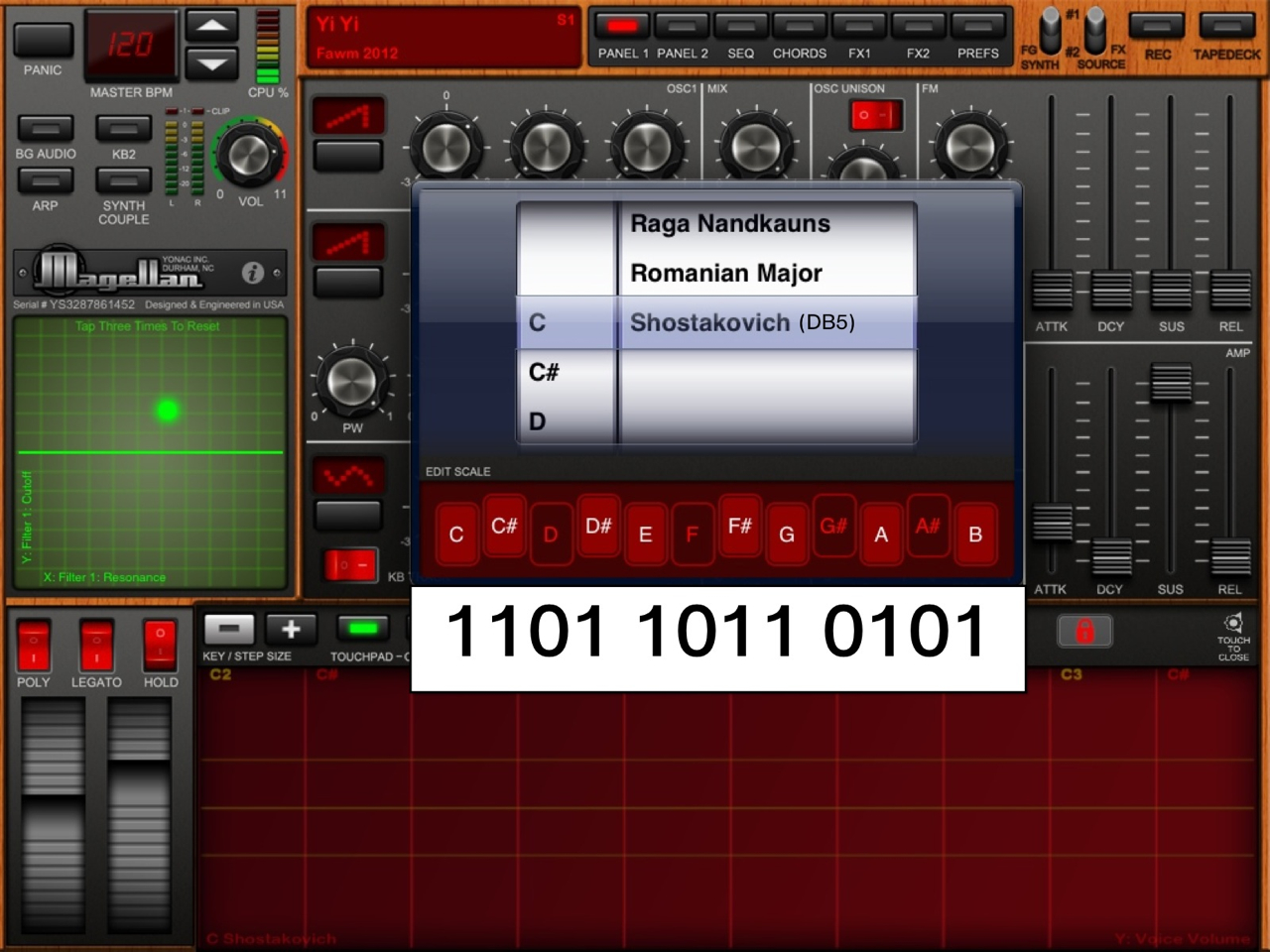
Any scale can be represented in binary form by using 1’s for notes that are present and 0’s for those that are not. For example, the Major scale can be represented as 101011010101. There is some very useful data there, but it would be difficult to remember dozens or hundreds of binary scale codes, let alone try to communicate that way. So let’s do this:

1010 1101 0101

A little easier to digest in chunks. The same data apparent in the smooshed together version is still there, but now there’s a bit more - something useful to real, live, practicing musicians: fingerings. It’s a lot easier to think in 4’s than in 12’s, especially for guitarists, who are already used to figuring out which of their 4 fret-hand fingers to use for a scale. We can also more easily compare the parts of a scale and compare one scale to another.

But… It’s still a bit unwieldy, hard to remember, difficult to use at band practice, etc. So let’s make the scale code smaller, easier to remember, speakable, and usable. Let’s convert those binary clusters into hexadecimal:

1010 1101 0101 = AD5

AD5: now that’s a little more managable. With this method, we can represent any of those 2048 unique scales with 3 digits. The codes are memorable, speakable and usable. With about an hour of practice, the average person can get the hang of converting single hexadecimal digits to 4-digit binary and back in their head with relatively little effort.
---

Here's another post showing the naming system applied to the scales from Magellan: http://musicin2d.com/post/43036923326/xenome-scale-reference-for-magellan-scale

Hopefully it makes a bit more sense with some real context. The underlying purpose is to simplify the classification of scales and define a way of referencing individual scales in conversation, etc.

[Rob Fielding]

It is a pretty good fingering visualization if you move back 1 fret as you go up a string. (5 bits would cover a fourth tuning. But with 4 bits you have only a span of a maj third). So, you cut the scale span into 3 equal parts and give them names. The names are just their binary values if you imagine frets being on or off. What makes it too wierd for most people will be that the names are a maj third apart, rather than a fourth.

It is very near to the idea of giving tetrachords names, and basing your whole music theory on stacks of tetrachords rather than full scales. (A tetrachord is basically a half-scale, the shape of the scale over a span of a fourth - where it is usually assumed that the fourth and fifth over the root are allowable.)

The real problem is that it obscures how to move from one shape to another. Scales adjacent in the fifths circle should be close; somehow. Ie:

0,0 - (rootMidiNote, sharps) = c major
0,1 - c with a sharp f
0,-1 - c with a flat b, etc

There would be more modifiers to twist the shape for melodic minor, etc.

Sent from my iPhone, which is why everything is misspelled. http://rfieldin.appspot.com
http://rrr00bb.blogspot.com

[Clifton Johnston]

Right on all counts regarding mapping xenomes (what I call these 3-digit clusters) to the guitar fretboard. In standard tuning, C Major, or C-AD5, would start at the 8th fret on the 6th string, 7th fret on the 5th string, etc. it obviously maps more cleanly to stringed instruments normally tuned in maj thirds. I did come up with an alternate guitar tuning for exploring this without changing string gauges or adjusting truss rods: E Ab C Ab C E. Mapping to guitar is only one small part of the potential for this, though, so I don't want to totally get hung up there.

I am familiar with the concept of tetrachords, which is quite useful, and in traditional harmonic terms, probably more useful. However, it does require a deeper understanding of theory to navigate and isn't widely used as a naming mechanism, meaning it's unfamiliar to the average musician. In addition, at least as I understand it, the tetrachord approach is generally confined to traditional 7-note diatonic scales - i.e. a 6-note scale missing the fifth would be impossible to name. I'm not an expert, so I could be missing something.

As far as relating the naming convention to the circle of fifths, I'm not entirely sure I understand your concern, so please clarify if you would. My system names scales/modes relative to the tonic, regardless of the actual tonic note (C, F, etc.). So C Maj would be C-AD5, F Maj would be F-AD5, and so on. I consider part of the value of the system to be that it's not centered around the C Major scale, or any scale. Any ordered set of notes can be represented from one (800) to twelve (FFF). Therefore intervals, chords, and scales with any number of notes can be named.

It is possible to do things like find scales containing a major 3rd interval, which would fall at the first bit from the left of the second binary cluster. Mathematically, that means your second digit will be 8-F in hexadecimal, so possible scales could be represented something like [8-F][8-F][0-F]. The set of scales containing the notes of the tonic's major triad might be represented as [8-F][9,B,D,F][0-F]. While it may seem a bit complex at first glance, the reality is that you can do this sort of thing in your head quite quickly once you understand it. It would be entirely possible to play through the possible scales in those sets without ever sitting down with pen and paper to figure it all out.

I appreciate you taking the time to discuss this :)

Sent from my iPad

[Rob Fielding]

My daughter's piano lessons include this exercise with scales, where I am making up the explanatory names:  (whole,half patterns)

whw - "minor tetrachord"

hww - "phrygian tetrachord"

wwh - "major tetrachord"

This is something that's all over the place in piano books that little kids are learning right now.  They do these patterns fourths, fifths and octaves apart for practice.  So this is no stretch to include it prefixed with the starting interval:

Iwhw    - C D Eflat F

IVwhw  - F G Aflat Bflat

If you read about Maqam, this is how they write them down; in a relative rather than absolute sense.  You can use numbers rather than the "whole"/"half" notation.  If half is "1", and whole is "2" (semitones), then Arabic music notation describes everything like:  "212", "122", "3/2 3/2 2" (yes, that's 3/2 ... half way between a whole and half tone.).  Then there is the shape you see associated with melodic minor shapes .. "1 3 1" (ie: E F G# A).  So, when you go to read your ethonmusicological scale-botany dictionary, they will describe things like "hijaz", "bayati", etc... as entire 7-note scales; which is a bit of a fiction created to try to fit it into piano notation.  But it's better to think of it more like a chord in a scale, with the notes that are melodically relevant along with the current root.  So, just pick a root note number from 0 to 11 (chromatic fret).  Then specify the shape with these numbers.  It's not as wierd as using binary.  It's ancient practice.  And it admits fractional steps without having to throw a grenade into the whole notation.

http://rfieldin.appspot.com
http://rrr00bb.blogspot.com

[Clifton Johnston]

I'm definitely not looking to replace traditional music theory. My naming system augments existing conventions where they fail or are less than optimal. For example, the "whw" naming mechanism breaks down with intervals larger than a whole step, and even where it does work, it is unwieldy as a way of referring to a specific scale in conversation. It makes no sense to refer to the C Major scale as Cwwhwwwh or Cwwh Gwwh. C Major in my system is C-AD5.

Tetrachords are useful for diatonic 7-note scales, and to some degree the modes of the Harmonic and Melodic Minors. They are useless for non-heptatonic scales. They are also somewhat unwieldy as naming conventions, where C Lydian Dominant becomes C Mix/Lyd, for example, vs. C-AB6 in my system. 

Most of the scales covered nicely by tetrachord conventions already have more conventional names by necessity. Tetrachords also require some degree of memorization, as you have to know what the intervals of the harmonic minor and minor lydian tetrachords are before being able to derive the notes of the Gypsy Minor scale from Har.Min/Min.Lyd. Gypsy Minor in my system is B39, which is not only easier to say and remember, but you can derive the notes directly from the name. This aspect is especially valuable when you get into scales that don't have names at all. 

The numeric system is more robust, but still doesn't really provide a good "handle" for general conversation or visual shorthand. Unlike the tetrachord method, you can't abbreviate numbers, so  a 7-note scale with a specified tonic will always be 8 digits, ala C2212221 for C Major.

The brief nature of xenomes offers a lot of benefits not only conversationally, as mentioned, but also as visual shorthand like my Magellan example:

Some of the problems with common scale names beyond the modes of the major scale are that they can be long, most musicians won't know Enigmatic Minor from Neapolian Major without research, and some scales just simply don't have common names. I'm definitely not suggesting anyone forego common scale names altogether, because they are just as useful, and in the case of the most common ones, much more useful than my scale codes. They just don't cover all of the bases, and without prior knowledge of a given scale, the name is purely arbitrary, providing no usable information. 

If I asked readers to list the notes of the C# Hungarian Major scale without removing their eyes from the screen, I'd be surprised if anyone could do it. However, just based on the info in this thread, I think an acceptable number of readers could list the notes of C#-9B6 without looking away. Or even a totally arbitrary scale like G-DF4, a no-name octatonic scale. 

Combined with the ability to derive all of the harmonic information from the scale name, the ability to name any combination of notes consistently in a form that can be communicated to other musicians opens up a lot of possibilities for exploring beyond common traditional harmonic theory. 

As for fractional steps, microtonality and xenharmonics, the current western naming conventions don't cover them very well, or at all, and traditional notation has to be bent quite a bit to accomodate them. My system could easily be extended to cover 19 or 51 notes per octave by increasing the number of digits, but I think that would reduce the value of the system for the 99% of musicians who will find 2048 unique note combinations in 12 different keys more than enough territory to explore, especially since the majority of music produced in our lifetime has come from a much smaller subset of scales. 

Sent from my iPad