Peirce's 1870 "Logic Of Relatives"
Jon Awbrey
At: http://inquiryintoinquiry.com/2019/09/24/peirces-1870-logic-of-relatives-%e2%80%a2-overview/
My long ago encounter with Peirce's 1870 paper, "Description of a Notation for the Logic of Relatives,
Resulting from an Amplification of the Conceptions of Boole's Calculus of Logic", was one of the events
precipitating my return from the hazier heights of philosophy to the solid plains of mathematics below.
Over the years I copied out various drafts of my study notes to the web, consisting of selections from
Peirce's paper along with my running commentary. I later serialized these notes to my blog and put all
the links on an Overview page. Please see the blog post linked above for the rest of the Overview.
Regards,
Jon
inquiry into inquiry: https://inquiryintoinquiry.com/
academia: https://independent.academia.edu/JonAwbrey
oeiswiki: https://www.oeis.org/wiki/User:Jon_Awbrey
isw: http://intersci.ss.uci.edu/wiki/index.php/JLA
facebook page: https://www.facebook.com/JonnyCache
John Bottoms
Jon,
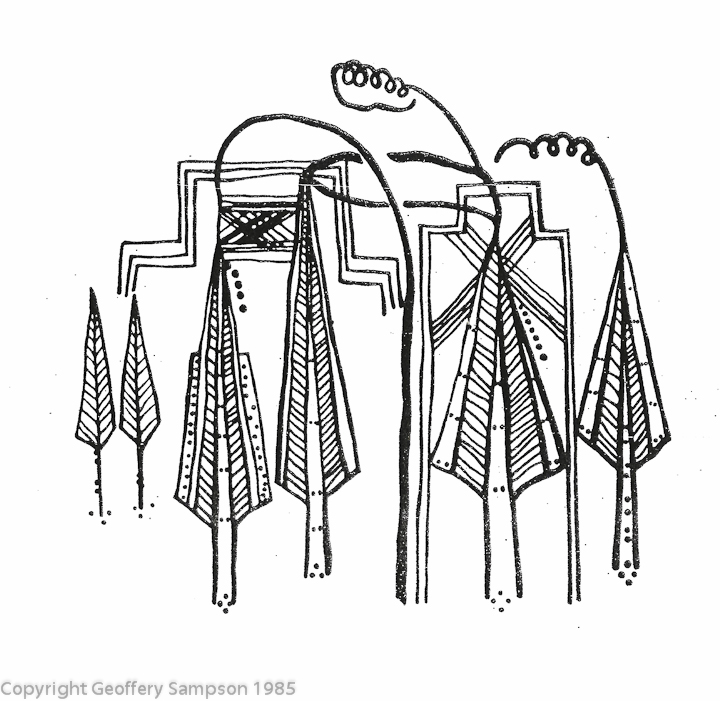
One of my interests is in the intersection between images and
prose. The note by Peirce "Proto-Graphical Syntax (Comment 7.1)
is prescient. It echo's a smasiograhic image that has been
discussed recently on the web. The image below shows two houses,
and the tree shapes represent people.
In the image a girl complains to her ex-lover that his new relationship is not useful, and he is missing an opportunity to have children with her. This image was created by a Yukaghir girl for a local game similar to Pictionary.
http://historyview.blogspot.com/2011/10/yukaghir-girl-writes-love-letter.htm
Jon Awbrey
At: http://inquiryintoinquiry.com/2019/09/30/peirces-1870-logic-of-relatives-%e2%80%a2-discussion-1/
John Bottoms, writing in the Ontolog Forum, compared the graphic
I drew for one of Peirce's relational formulas to a pictographic
image he had been studying.
Peirce introduced the compound term "giver of a horse to a lover of a woman"
in Selection 7 to illustrate his use of marks of reference to identify the
corresponding correlates of component terms. The symbolic form of this
compound term is shown below.
http://s0.wp.com/latex.php?latex=%5Cmathfrak%7Bg%7D_%7B%5Cdagger%5Cddagger%7D+%7B%7D%5E%5Cdagger%5Cmathit%7Bl%7D_%5Cparallel+%7B%7D%5E%5Cparallel%5Cmathrm%7Bw%7D+%7B%7D%5E%5Cddagger%5Cmathrm%7Bh%7D&bg=FDF9EF&fg=000000&s=2
In my comment on Proto-Graphical Syntax I drew lines of identity to connect
the corresponding marks of reference, as shown in the following Figure.
Figure 1. Giver of a Horse to a Lover of a Woman
https://inquiryintoinquiry.files.wordpress.com/2014/02/lor-1870-figure-3.jpg
John tells us what he sees in this Figure in the following words:
<QUOTE>
semasiographic image that has been discussed recently on the web.
In the image a girl complains to her ex-lover that his new relationship
is not useful, and he is missing an opportunity to have children with her.
This image was created by a Yukaghir girl for a local game similar to
Pictionary.
https://inquiryintoinquiry.files.wordpress.com/2019/09/geoffery-sampson-e280a2-a-yukaghir-girl-writes-a-love-letter.jpg
</QUOTE>
I started a draft in the middle of the night to draw out
the analogies and disanalogies of these two Figures but
the clear light of day showed me I would need to deal
with a host of preliminary issues before moving on.
So I will turn to that task next.
Regards,
Jon
Jon Awbrey
At: https://inquiryintoinquiry.com/2019/10/06/peirces-categories-%e2%80%a2-8/
When Threads Collide ...
Questions about Peirce's Categories arose in a couple of Facebook discussions,
giving me a chance to tackle a number of issues that often lead people astray.
As usual, most problems in Peirce's thought can be cleared up by duly diligent
applications of his pragmatic maxim and his relational logic working in tandem.
As one might anticipate, then, my answer to the question of Peirce's categories
has one foot already under our present head.
The best way to get clear about Peirce's categories is to look to their
origin in Aristotle's concept of a category, in effect nothing more
mysterious than a grammatical device for reducing the ambiguities
of equivocal terms. We find Peirce starting out this way in his
classification of logical terms, for instance, here:
* Peirce's 1870 "Logic Of Relatives" : Selection 1
: https://inquiryintoinquiry.com/2014/01/27/peirces-1870-logic-of-relatives-%e2%80%a2-selection-1/
Regards,
Jon
Jon Awbrey
At : http://inquiryintoinquiry.com/2019/10/07/peirces-categories-%e2%80%a2-9/
Here's my response to a comment in the Systems Sciences Facebook Group,
questioning whether I might be comparing apples and oranges in lumping
philosophical and mathematical categories under the same head.
Scanning the spectrum of sources I sampled in my Precursors of Category Theory,
there are many differences in the categorical paradigms different observers
developed over the centuries. Just for starters, the numbers of categories
vary widely from system to system. But there is a conceptual continuity in
the "function" category markers perform in every system. If we look to the
role a category marker plays in the relation between formal expressions and
their formal objects, in effect, if we look at the matter from a semiotic
perspective, as Aristotle already did, then we see the job of a category
marker is to reduce ("drive down") the ambiguity of equivocal linguistic
expressions to the point where they obey the laws of logic.
Resources
=========
* Logic Syllabus : Relational Concepts
https://oeis.org/wiki/Logic_Syllabus#Relational_concepts
* Precursors Of Category Theory
https://oeis.org/wiki/Precursors_Of_Category_Theory
* Survey : Precursors Of Category Theory
https://inquiryintoinquiry.com/2015/05/15/survey-of-precursors-of-category-theory-%E2%80%A2-1/
Jon Awbrey
There is a kind of "second cousin" kinship between category markers, tenses,
modalities, etc. In several drafts of the previous note I experimented with
grammatical terms like conjugation, declension, diacritic, inflection, etc.
to explain the function of category markers. But I eventually decided this
laid too much stress on their grammatical aspect and distracted from their
main function, which is to focus the relation between formal expressions
and formal objects.
I think it would help to clarify the sorts of formal expressions ("signs")
and formal objects (mostly "mathematical objects") I currently have in mind
to post a bit of content from an earlier discussion in several other groups.
I'll get to that after dinner ...
Regards,
Jon
On 10/8/2019 4:09 PM, Helmut Raulien wrote:
> Jon, List,
> for me a simple category marker is the connection of tenses:
> Something providing a connection between past and present
> is of category 1, between present and future category 2,
> and between past and future category 3.
> Best,
> Helmut
Jon Awbrey
At: https://inquiryintoinquiry.com/2019/10/08/peirces-categories-%e2%80%a2-10/
I began that note on the "Precursors of Category Theory" as a purely
exploratory sketch, plotting a few points on a single theme with no
plans of making an exhaustive survey. Even at that I never got time
to get back to it. I put in a pin for Kant but haven't had a chance
to map out any passages. There are even "incitements" going back to
my earliest days reading Russell and wrestling with his take on type
theory but those inklings are too hazy in my memory to make clear at
present.
John F. Sowa
Jon,
> whether I might be comparing apples and
oranges in lumping philosophical and mathematical categories under the
same head... there are many differences in the categorical paradigms
different observers developed over the centuries.
There are two kinds of people: lumpers and splitters. On this issue, one could argue for a single lump, as you do. The mathematical category theory is so general that it could be applied to the philosophical theories.
But the kinds of problems that the mathematical theory was designed to solve are very different from the philosophical problems that Aristotle, Porphyry, Kant, and Peirce were trying to solve.
I believe that the pedagogical issues tip the balance in favor of the splitters. It's easier to explain the philosophical issues without bringing in the mathematical theory, and it's easier to explain the mathematical theory without bringing in the philosophical issues. The only people who could understand the application of the mathematical theory to the philosophical issues are those who already have a deep understanding of both. That group is very small, very sophisticated, and they don't need an elementary tutorial.
John
Jon Awbrey
At: https://inquiryintoinquiry.com/2019/10/12/peirces-categories-%e2%80%a2-12/
John, Jeff, All ...
Different minds are drawn to Peirce for different reasons
and they tend to discover different stores of value there.
I was attracted to his work largely for his insights into
logic, math, and science and because his articulations of
their springs and catches ring true to the ways their own
practitioners understand them in practice.
One consequence is my tendency to approach the question of
categories from a particular angle, more through the logic
and mathematics of relations than by way of phenomenology.
What follows from that approach gives me sufficient reason
to pursue it, but I'll have to save further motivation until
I develop more material from Peirce's 1870 Logic of Relatives.
Regards,
Jon
John F. Sowa
Jon A, List
I strongly agree with your emphasis on Peirce's mathematics and logic, which were the foundation for his way of thinking, writing, and research from early childhood to the end. But we should also emphasize that all exact thinking in every field is diagrammatic and mathematical. That includes phenomenology and the derivation of the semeiotic categories by the application of mathematics to phenomenology.
To emphasize that point, I'll cite
Leonardo da Vinci, who is often called a renaissance genius. He was
certainly a genius who lived in the Renaissance, but the essence of his
genius was his exact diagrammatical -- hence mathematical --
reasoning.
Although Leonardo had never studied mathematics, he was one of the most creative *applied* mathematicians of all time. Just today, I came across a computerized analysis of a bridge design that had not been built. The analysis showed that his design was structurally sound and that it included safety features that were not re-invented for another 300 years. Unlike the infamous Tacoma Narrows bridge, Leonardo's design could withstand high winds. See https://techxplore.com/news/2019-10-leonardo-da-vinci-bridge.html
That article shows the complexity of the design and the computerized construction (with a 3-D printer) that was required to build and test a model.. This is one of many examples of Leonardo's ability to visualize complex 3-D structures that are (a) mathematically correct, (b) physically sound, and (c) fit for purpose as engineering designs.
Leonardo's diagrammatic reasoning was also the foundation for his studies of anatomy and their application in his art. He dissected many animals and human cadavers in order to study the structure of the bones, muscles, and flesh that determined the shapes and motions of their bodies. The precision of his diagrammatic analysis enabled him to produce the most lifelike art of his day (or even of all the days since then).
In his discussions of phenomenology, Peirce had a high regard for artists who are able to analyze their perceptions with mathematical precision. That is the essence of phenomenology. Peirce also had a low opinion of "metaphysicians" who did not have the ability to do diagrammatic reasoning.
Another non-mathematician who was a genius at precise diagrammatic reasoning was Michael Faraday. He could visualize electrical and magnetic fields and their dynamic interactions. To develop his famous equations, Maxwell spent many hours working with Faraday in order to translate Faraday's phenomenological insights to partial differential equations.
Moral of the story: Phenomenology requires the utmost precision in diagrammatic reasoning and in the translation of that reasoning to engineering designs, anatomical drawings, artistic creations, and formal notations in science, mathematics, music, logic, and computer science.
For more examples of the importance of visualization in mathematics itself, see http://jfsowa.com/talks/ppe.pdf .
John
bruces...@cox.net
I line up these groups in a single aligned polarity:
Bottom-up --> <-- Top-down
Splitters Lumpers
Scruffies Neats
Local Global
At the bottom, small precise units of a perhaps implicit whole (I'd call this "the empirical ground" -- some people might call it "reality")
At the top, big units of a fuzzy explicit whole (a vague fuzzy sense of wholeness, like "a circle that contains everything" -- "the set of all sets")
Splitters work from the top-down, breaking units into a subunits, so they are "moving to the left" in this framework ("from higher to lower")
Lumpers work from the bottom up, combining what they perceive to be sub-units into integrating wholes, so they are "moving to the right" ("ascending the staircase") in this spectrum ("from lower to higher")
Scruffies are working on immediate and "local" problems that they think might be logically independent of any supposed all-containing super-unit. Some would call them "relativists". For them, it's enough to work on a fragment, because after all there is no primary agreed-upon universal unit, and might never be.
Neats are working from the top down, looking for elegance and simplicity, in deterministic chains they believe are implicit in their integrating unitary foundation.
This is the primary philosophic/scientific/semantic dichotomy that describes everything people anywhere are doing. All ideas, all thought-forms, or political ideas -- indeed, any concept whatsoever -- are organized ("can be organized") somewhere on this spectrum. There are many metaphors in philosophy that describe this framework ("great chain of being" -- or "hierarchy" -- or "tree")
But truly -- the spectrum remains fragmented and uncertain, so the subject quickly becomes (perhaps overwhelmingly) messy in the real-world context of immediate heuristic problem solving.
"All reality is local" -- true from an orthodox ("reductionist") scientific perspective, but perhaps misleading and short-sighted from a philosophic perspective.
*
PS -- After I read my draft of this note, I made a small addition. I changed the wording "all ideas ARE organized on this framework" to "all ideas CAN BE organized" this way. It's not a scientific/empirical observation: it's a postulate, a hypothesis, a proposal, a method, a guiding principle.
"You don't want a crazy fragmented (and enraged) world? -- try this."
Bruce Schuman
Santa Barbara CA USA
All contributions to this forum are covered by an open-source license.
For information about the wiki, the license, and how to subscribe or
unsubscribe to the forum, see http://ontologforum.org/info/
---
You received this message because you are subscribed to the Google Groups "ontolog-forum" group.
To unsubscribe from this group and stop receiving emails from it, send an email to mailto:ontolog-foru...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/ontolog-forum/a233f358579a31c2c63f0c8032ab25da.squirrel%40webmail2.bestweb.net?utm_medium=email&utm_source=footer.
Jon Awbrey
At: https://inquiryintoinquiry.com/2019/10/22/peirces-1870-logic-of-relatives-%e2%80%a2-comment-1/
Re: The Difference That Makes A Difference That Peirce Makes : 31
At: https://inquiryintoinquiry.com/2019/10/21/the-difference-that-makes-a-difference-that-peirce-makes-31/
If you concur with the diagnosis of present lapses I gave
on the "Difference" thread, the question becomes: How to
remediate "a failure to comprehend the relational paradigm,
especially triadic relations, their irreducibility, and the
consequences thereof"?
My answer to that naturally brings me back to this thread,
and so I'll continue from this point ...
Regards,
Jon
Jon Awbrey
At: https://inquiryintoinquiry.com/2019/10/22/peirces-1870-logic-of-relatives-%e2%80%a2-comment-2/
I was a little tired when I wrote that last post, and wasn't too
happy with how it read in the morning, so here's another attempt --
***
In a recent post on a thread devoted to incidental issues,
I gave this assessment of our present situation:
One of the more disconcerting developments, I might say "devolutions",
I've observed over the last 20 years has been the general slippage
back to absolutist and dyadic ways of thinking, all of it due to the
stubborn pull of unchecked reductionism and a failure to comprehend
the relational paradigm, especially the basic facts about triadic
relations, their irreducibility, and the consequences thereof.
For anyone who sees our situation this way, and who thinks it
calls for a remedy, the question becomes: How to remediate
a persistent failure to comprehend the relational paradigm,
especially the basic facts about triadic relations, their
My answer to that naturally brings me back to this thread,
Regards,
Jon
Jon Awbrey
At : http://inquiryintoinquiry.com/2019/10/24/peirces-1870-logic-of-relatives-%e2%80%a2-discussion-2/
Re : Peirce's 1870 "Logic Of Relatives" : Comment 2
At : https://inquiryintoinquiry.com/2019/10/22/peirces-1870-logic-of-relatives-%e2%80%a2-comment-2/
My previous comment summed up my observations of a general drift toward
"absolutist and dyadic ways of thinking" in the communities of inquiry
I've known since the turn of the century. I traced its cause to "the
stubborn pull of unchecked reductionism" and a corresponding failure
to grasp the relational determinants of complex phenomena.
That last phrase gave me a lot of trouble -- I vacillated between it
and "the unchecked pull of stubborn reductionism" before flipping a coin
going with the one I wrote. To clarify, we are talking a preference for
simple models and theories which is natural enough so long as the chosen
models and theories are up to the task of explaining the phenomena, but
which becomes irrational and unnatural if it persists in the face of
steadily mounting anomalies.
That is my description and my diagnosis of present conditions
as I see them. I could be wrong about either or both. But the
reason for bringing all that up is not to raise a wail of general
lamentation. The purpose of a diagnosis is to indicate a remedy.
Regards,
Jon
Jon Awbrey
At: http://inquiryintoinquiry.com/2020/04/15/peirces-categories-%e2%80%a2-13/
Re: Peirce List ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/thrd1.html#00020 )
Re: Robert Marty ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/msg00020.html )
All,
With a few choice exceptions I have always found Peirce’s earlier writings on categories, relations, and semiotics to be
more clear, exact, and fruitful in practice than his last attempts to explain himself without the requisite logical and
mathematical supports.
Still, I like Robert Marty’s “podium” picture of the universal categories
( https://academia.edu/resource/work/41574474 ), comprehend it all or not,
and I found myself once using a similar picture to explain the relationships
among the big 3 normative sciences of aesthetics, ethics, and logic. I called
this “The Pragmatic Cosmos”, using “cosmos” in the sense of a global order.
It looks like most of this stuff has fallen off the live web but here's
a few links I found.
* The Pragmatic Cosmos (Oct 2003)
http://web.archive.org/web/20061014010215/http://stderr.org/pipermail/inquiry/2003-October/000879.html
* Inquiry Oriented Systems (Feb 2004)
http://web.archive.org/web/20070222005725/http://suo.ieee.org/ontology/thrd4.html#05337
• 1. http://web.archive.org/web/20070302154925/http://suo.ieee.org/ontology/msg05337.html
… 8. http://web.archive.org/web/20070302155036/http://suo.ieee.org/ontology/msg05344.html
* The Pragmatic Cosmos (Mar 2012)
https://www.mail-archive.com/peir...@listserv.iupui.edu/msg00924.html
I'll copy and format pieces of this to my blog as I get time.
Resources
=========
* Peirce's 1870 Logic Of Relatives
https://oeis.org/wiki/Peirce%27s_1870_Logic_Of_Relatives_%E2%80%A2_Overview
Jon
inquiry into inquiry: https://inquiryintoinquiry.com/
academia: https://independent.academia.edu/JonAwbrey
oeiswiki: https://www.oeis.org/wiki/User:Jon_Awbrey
Jon Awbrey
At: http://inquiryintoinquiry.com/2020/04/16/peirces-categories-%e2%80%a2-14/
Continuing with the discussion of Robert Marty's “Podium Diagram” ...
RM: What do you think of the presuppositions between the levels? Do they make sense to you?
At this point I have mostly questions, which would take further research to answer, not to mention unpacking many books
still in boxes from our move a year and a half ago, none of which I'm at liberty to do right now. So, just off the cuff ...
“Presupposition” is one of those words I tend to avoid, as it has too many uses at odds with each other. There are at
least the architectonic, causal, and logical meanings. It it were only a matter of logic, I would say “P presupposes Q”
means “P ⇒ Q”. But usually people have something more pragmatic or rhetorical in mind than pure logic would require,
something like enthymeme.
It's also common for people to confound the implication order “P ⇒ Q” with the causal order “P causes Q”, whereas it's
more like the reverse of that. In more complex settings we usually have the architectonic sense in mind, and that is
what I sensed in the case of the normative sciences. Viewed with regard to their bases, logic is a special case of
ethics and ethics is a special case of aesthetics, but with regard to their level of oversight, aesthetics must submit
to ethical control and ethics must submit to logical control.
Early on, Peirce used “involution” with the meaning it has in arithmetic or number theory, namely, “exponentiation”,
where x^y means taking x to the power of y. See the following passage and commentary.
* Peirce's 1870 Logic Of Relatives • The Sign of Involution
https://oeis.org/wiki/Peirce%27s_1870_Logic_Of_Relatives_%E2%80%A2_Part_2#Selection_12
As far as the boolean or propositional analogue goes, x^y for x, y in {0, 1} means the same thing as x ⇐ y, as one can
tell by comparing the following two operation tables.
Exponentiation and Converse Implication
https://inquiryintoinquiry.files.wordpress.com/2020/04/exponentiation-and-converse-implication.png
I haven't looked into whether Peirce uses “involution” or “involvement” with that sense in his later writings.
Jon Awbrey
At: https://inquiryintoinquiry.com/2020/05/01/peirces-categories-%e2%80%a2-15/
Robert Marty wrote: <QUOTE>
I submit for your review this preprint which is awaiting publication:
The Podium of the Universal Categories of C.S. Peirce
=====================================================
https://academia.edu/resource/work/41574474
Abstract
========
This article organizes Peirce’s universal categories and their degenerate forms from their presupposition relationships.
These relationships are formally clarified on the basis of Frege’s definition of presupposition. They are visualized
in a “podium” diagram. With these forms, we then follow step by step the well-known and very often cited third Peirce
Lowell Conference of 1903 (third draft) in which he sets out his entire method of analysis based on these categories.
The very strong congruence that is established between the podium and the text validates the importance, even the
necessity, of taking into account these presuppositions in order to correctly understand Peirce’s phenomenology.
I would be very happy to read your comments. </QUOTE>
There were numerous issues stemming from Robert Marty’s post and paper, some central and some tangential, which
attracted my interest and which I hope I can get back to. Seeing as how some of the earliest issues got a little lost
in the flood of discussion that followed I thought I would take a moment to record a few threads for future follow up.
* Subthread 1 ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/thrd1.html#00020 )
* Subthread 2 ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/thrd2.html#00046 )
* Subthread 3 ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/thrd8.html#00199 )
I made a start at rehashing some of these questions on my blog:
Semiotics, Semiosis, Sign Relations • 9
https://inquiryintoinquiry.com/2020/04/12/semiotics-semiosis-sign-relations-%e2%80%a2-9/
Peirce’s Categories • 13 • 14
https://inquiryintoinquiry.com/2020/04/15/peirces-categories-%e2%80%a2-13/
https://inquiryintoinquiry.com/2020/04/16/peirces-categories-%e2%80%a2-14/
Readings On Determination • Discussion 4
https://inquiryintoinquiry.com/2020/04/29/readings-on-determination-%e2%80%a2-discussion-4/
If I get inspiration and time enough, I may try to
organize the issues and further comment on my blog.
Regards,
Jon
Jon Awbrey
At: http://inquiryintoinquiry.com/2020/05/04/peirces-categories-%e2%80%a2-16/
A feature of particular interest to me in Robert Marty’s paper is the resonance he finds between category theory, as
it’s known in contemporary mathematics, and the study of Peirce’s Categories. I’ve long felt the cross-pollination of
these two fields was naturally bound to bear fruit. In that light I’ll refer again to the “brouillon projet” I wrote on
the Precursors of Category Theory, where I trace a common theme uniting the function of categorical paradigms from
Aristotle through Peirce to present day logic and math.
• Precursors Of Category Theory
https://oeis.org/wiki/Precursors_Of_Category_Theory
By way of orientation to the perspective I’ll adopt in reading Marty’s “Podium” paper, here’s the first of the excerpts
I collected, from a primer of category theory on the shelves of every student of the subject, giving a thumbnail
genealogy of categories from classical philosophy to current mathematics.
<QUOTE>
Now the discovery of ideas as general as these is chiefly the willingness to make a brash or speculative abstraction, in
this case supported by the pleasure of purloining words from the philosophers: “Category” from Aristotle and Kant,
“Functor” from Carnap (Logische Syntax der Sprache), and “natural transformation” from then current informal parlance.
🙞 Saunders Mac Lane • Categories for the Working Mathematician, 29–30.
</QUOTE>
Resource
========
• Survey of Precursors Of Category Theory
https://inquiryintoinquiry.com/2015/05/15/survey-of-precursors-of-category-theory-%e2%80%a2-1/
Regards,
Jon
Jon Awbrey
At: http://inquiryintoinquiry.com/2020/05/07/peirces-categories-%e2%80%a2-17/
All,
I've been too immersed in the Peirce List discussion of Robert Marty's “Podium” paper to write much here — before I lose
track of what I've been thinking the last several days I'll need to ravel up my off-the-cuff remarks and pen them on the
sleeves of this blog.
Re: Peirce List
https://list.iupui.edu/sympa/arc/peirce-l/2020-04/thrd1.html#00020
https://list.iupui.edu/sympa/arc/peirce-l/2020-05/thrd2.html#00003
Re: Helmut Raulien
https://list.iupui.edu/sympa/arc/peirce-l/2020-04/msg00027.html
https://list.iupui.edu/sympa/arc/peirce-l/2020-05/msg00057.html
Helmut Raulien asked several questions about the composition, irreducibility, and reducibility of relations. For
background on relation composition as Peirce originally treated it, I referred him to Peirce's 1870 Logic Of Relatives,
especially the section titled “The Signs for Multiplication”, along with my commentary linked below.
• Peirce's 1870 Logic Of Relatives
https://oeis.org/wiki/Peirce%27s_1870_Logic_Of_Relatives_%E2%80%A2_Overview
There is also this article:
• Relation Composition
https://oeis.org/wiki/Relation_composition
For readers who want to skip to the chase for the quickest possible overview, the sorts of pictures floating through my
head when I'm thinking about relational composition are the bipartite graph or “bigraph” pictures in the following section.
• Relation Composition • Graph-theoretic Picture
https://oeis.org/wiki/Relation_composition#Graph-theoretic_picture
I see these old articles have grown a bit dusty —
I'll be working to improve the graphics and text as I get time.
Resources
=========
Jon Awbrey
At: http://inquiryintoinquiry.com/2020/05/12/peirces-categories-%e2%80%a2-18/
Re: Peirce's Categories • 15
At: https://inquiryintoinquiry.com/2020/05/01/peirces-categories-%e2%80%a2-15/
track of tricky points coming up in discussion which cry out for further discussion but then “human voices wake us, and
we drown” or something … So let me go back to the list of loose ends I put together at the first of the month and try to
address a few of them.
Here's one juncture deserving of another look:
• JAS ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/msg00024.html )
• JA ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/msg00026.html )
• HR ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/msg00027.html )
• JAS ( https://list.iupui.edu/sympa/arc/peirce-l/2020-04/msg00028.html )
<QUOTE> JAS:
Every proposition is collective and copulative; as I stated in a recent post
( https://list.iupui.edu/sympa/arc/peirce-l/2020-03/msg00028.html ) , its
dynamical object is “the entire universe” (CP 5.448n, EP 2:394, 1906), which
is “the totality of all real objects” (CP 5.152, EP 2:209, 1903), while its
immediate object is “the logical universe of discourse” (CP 2.323, EP 2:283, 1903).
</QUOTE>
This is a very important point, not the least because of the
light it throws on a question John Corcoran raised on Facebook
( https://www.facebook.com/groups/peircesociety/permalink/1861963543939629/ )
and elsewhere (
https://www.academia.edu/s/7ee6dbf0ce/the-principle-of-wholistic-reference-previously-manuscrito-27-2004-159-71-cite-as-manuscrito-30-2007-493-505-p-r
)
as to whether the logical universes of Peirce, or logicians in
general, are conceived as referring to something like a holistic
totality of existence or only a more limited universe of discourse
relevant to a particular discussion. I thought that significant
enough to blog on it here:
• Semiotics, Semiosis, Sign Relations • 9
https://inquiryintoinquiry.com/2020/04/12/semiotics-semiosis-sign-relations-%e2%80%a2-9/
<QUOTE> JA:
Incidentally … lack of care in distinguishing different objects of the same signs, in particular, immediate and ultimate
objects and their corresponding universes or object domains, has been the source of many misunderstandings in scattered
discussions on Facebook of late.
</QUOTE>
But then I added:
<QUOTE> JA:
Another issue arising here has to do with the difference between the “dimensionality of a relation” and the “number of
correlates”. Signs may have any number of correlates in the object domain without requiring the dimensionality of the
relevant sign relation to be greater than three. This is one of the consequences of “triadic relation irreducibility”.
</QUOTE
And that raised a number of further replies from HR and objections from JAS … which I'll say more about when I get a chance.
Jon Awbrey
At: http://inquiryintoinquiry.com/2020/05/13/peirces-categories-%e2%80%a2-19/
More discussion of Robert Marty's “Podium” diagram:
https://www.academia.edu/41574474/The_podium_of_the_universal_categories_of_C.S.Peirce
Another point where the onrush of discussion and the impact of worldly distractions caused my train of thought to jump
the track is here:
<QUOTE> RM:
https://list.iupui.edu/sympa/arc/peirce-l/2020-05/msg00054.html
First I note that the formulation “3ns involves 2ns, which involves 1ns” is very dangerous [as] it forgets that 2ns has
its autonomy and 1ns too. If you look at the podium [one] remains in the inner cylinder. It seems to me that Peirce's
reproach to Hegel is:
“He has usually overlooked external Secondness, altogether. In other words, he has committed the trifling oversight of
forgetting that there is a real world with real actions and reactions. Rather a serious oversight that.”
It is therefore important to prefer “3ns involves 2ns and 1ns, while 2ns involves 1ns” which preserves the autonomy of
the Peircian categories so as not to encourage the idea of a possible peircean hegelianism.
</QUOTE>
<QUOTE> JA:
https://list.iupui.edu/sympa/arc/peirce-l/2020-05/msg00056.html
I've been working on a comment about your first point but I'll post it … when and if I manage to put it in respectable
shape. Just by way of a hint for now, the issue turns on whether we take involves or presupposes to be a dyadic
relation and a transitive one at that, as we would if we pass from “3 involves 2” and “2 involves 1” to the conclusion
“3 involves 1”. That may be true for some concepts of involution or presupposition but I think the operative relation
in this case is a thoroughly irreducible triadic relation, one whose properties do not reduce to the composition of two
dyadic relations.
</QUOTE>
I think it will take a little more work to get clear about this.
I will go back to the draft remarks I was working on and see if
I can bring them to bear on the question.
Jon Awbrey
At: http://inquiryintoinquiry.com/2020/05/14/peirces-categories-%e2%80%a2-20/
More discussion of Robert Marty's “Podium” diagram:
https://www.academia.edu/41574474/The_podium_of_the_universal_categories_of_C.S.Peirce
thought, all the more so, even if that third person is not so formidable a thinker as Charles Sanders Peirce. Measures
of misunderstanding may be moderated if all thoughts and thinkers are guided by common objectives but the proof of the
pudding is in the partaking, as they say. So let's step carefully and focus on the task of determining whether category
theories, old and new, make good tools for understanding sign relations.
http://wikipediareview.com/smilys0b23ax56/default/stepcarefully.gif
The interaction recorded in my last post
https://inquiryintoinquiry.com/2020/05/13/peirces-categories-%e2%80%a2-19/
continued as follows:
<QUOTE> RM:
https://list.iupui.edu/sympa/arc/peirce-l/2020-05/msg00061.html
I do not see how we can talk here about an operative relationship that would be a triad relationship. It is not
anything other than the composition of two morphisms and I do not ask for more. 3, 2, and 1 are the “place names” and
“involves” are arrow names that I usually call alpha and beta. Now if you think about the determinations in the sign, I
have always assumed after much study of the 76 definitions, this idea that the composition of applications captures the
presence in the mind of each of the elements of the sign, in such a way that they are themselves ipso facto connected by
a triadic relationship. There is a relationship of tricoexistence that is established as in this case evoked by Peirce:
“It predicates the genuinely Triadic relationship of tricoexistence, P and Q and R coexist” (CP 2.318, unfortunately
there is a hole in my PDF of CP right after and I [left] my paper edition at the library of my university, inaccessible
at the moment).
We have a mutual incomprehension?
</QUOTE>
<QUOTE edited> JA:
https://list.iupui.edu/sympa/arc/peirce-l/2020-05/msg00072.html
I don't often join the debates over sign classification so frequently animating the animadversions of the Peirce List.
As more the observer than the participant I see the same pattern over and over, with occasional hints but never any hue
of resolution fast enough to last and satisfy every dyehard.
Situations of that sort are no novelty in philosophy, or politics, or even math and science on occasion. And when they
occur it is usually because the “place to stand” from which the subject appears in its proper light has yet to be
reached by every viewer.
So I'll back up a little and say how I see things from where I am.
</QUOTE>
Jon Awbrey
http://inquiryintoinquiry.com/2020/06/25/peirces-categories-%e2%80%a2-21/
Robert, All ...
Let us go back to a point where paths diverged in the yarrow wood and a lot of synchronicity was lost …
Variant understandings of words like axiom, definition, predicate, proposition, proof, relation, theory, and the like
make mutual understanding difficult. For example, when I mention Peirce's definition of a sign, many people will bring
to mind a long list of short statements Peirce made in describing the properties of signs, and when I refer to Peirce's
theory of signs, many people will bring to mind the entire corpus of Peirce's writings on signs, so far as they know it,
augmented perhaps with reliable reports of statements he may have made about signs.
There are fields of study where such expansive understandings of definitions and theories are the prevailing ones,
perhaps the only feasible ones. One example would be scriptural hermeneutics, where the full sense of a word's meaning
is determined by its use in every context where it occurs. Thus the use of concordances to bring the diversity of
contextual meanings into harmony. We plow this field in a hermeneutic circle, according each bit of authoritative text
equal priority, none privileged above the other, as if equidistant from a central point radiating a pervasive message.
It's all you can do when there's nothing but the text in view.
Curiously enough, the branch of mathematical logic known as model theory sets out with an equally expansive view, taking
a maximally inclusive definition of theory as its initial point of departure and defining a theory as an arbitrary set
of sentences from a formal language. Naturally, logical and mathematical attention almost immediately shifts to more
focused spheres of theory, as indicated in the following from a standard textbook.
<QUOTE>
A set Γ of sentences is called a “theory”. A theory is said to be “closed” iff every consequence of Γ belongs to Γ. A
set Δ of sentences is said to be a “set of axioms for” a theory Γ iff Γ and \Delta have the same consequences. A theory
is called “finitely axiomatizable” iff it has a finite set of axioms. Since we may form the conjunction of a finite set
of axioms, a finitely axiomatizable theory actually always has a single axiom. The set Γ' of all consequences of Γ is
the unique closed theory which has Γ as a set of axioms.
(Chang and Keisler, p. 12).
</QUOTE>
That's all well and good as far as esoteric technical usage goes but outside those cloisters I would recommend using the
word “corpus” when we want to talk about an arbitrary set of sentences or texts and to reserve the word “theory” for
those corpora possessing more differentiated and substantial anatomies than a mere hermeneutic blastula.
Reference
=========
• Chang, C.C., and Keisler, H.J. (1973), Model Theory, North-Holland, Amsterdam.
(p. 12) https://oeis.org/wiki/User:Jon_Awbrey/Mathematical_Notes#MOD._Note_14
