Metamath verifier in Zig
Marnix Klooster
Mario Carneiro
--
You received this message because you are subscribed to the Google Groups "Metamath" group.
To unsubscribe from this group and stop receiving emails from it, send an email to metamath+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/metamath/CAF7V2P_C7QcKP8b_rxvEO6e5uXTMpS6gySU-iVCiqLD1gCW5qQ%40mail.gmail.com.
Marnix Klooster
To view this discussion on the web visit https://groups.google.com/d/msgid/metamath/CAFXXJSvqg4vHT%2B4HmaBhHSMCTdE0-EX0vRyVr6_tn%3DYFGgJmGA%40mail.gmail.com.
--
Thierry Arnoux
Hello all,
My main goal is actually doing stuff (parsing statements... )I've also been interested in this, and did a few additions to the Rust-based SMM3 / smetamath-rs / metamath-knife, including recently simple parsing of set.mm formulas. I expect it will be easy to perform e.g. unification in that format.
The code is available at https://github.com/tirix/metamath-knife/tree/grammar,
it is a fork from David's metamath-knife (itself a fork of
Stefan's repository).
cargo run -- --timing --print_formula subset.mm
There are two steps, one for building the grammar from the
syntactic axioms $a and $f, and another one for parsing the $e and
$p statements into what I name "formula".
Finally, the option --print_formula flattens and outputs the
formulas back, to give a visual confirmation that the process
works.
However this parsing is not yet LALR(7) as required by
the set.mm grammar. I've been working on a subset of set.mm which
only includes first order logic and predicate calculus, for which
LALR(1) is sufficient (set.mm 's type codes are currently also
hard-coded, but this can be easily overcome by parsing the "$j
syntax" comments).
My next step will of course be to improve the current parser and
get LALR(7), but I thought it might already be worth sharing at
this early stage.
BR,
_
Thierry
PS. I'm very new to Rust and I still consider myself in the
process of learning, so if anyone is interested to review the
code, I could open a PR so that the changes appear clearly.
To view this discussion on the web visit https://groups.google.com/d/msgid/metamath/CAF7V2P_PM0_JE7zMQ61rFOYgX-RzUQc4RKqvLDAirE9SFwaBhg%40mail.gmail.com.
Thierry Arnoux
Hi Marnix, Stefan and all,
I've been slowly progressing in adding to SMM3 / metamath-knife the capability to parse the set.mm database, and although a few steps remain, I'd like to share where I am.
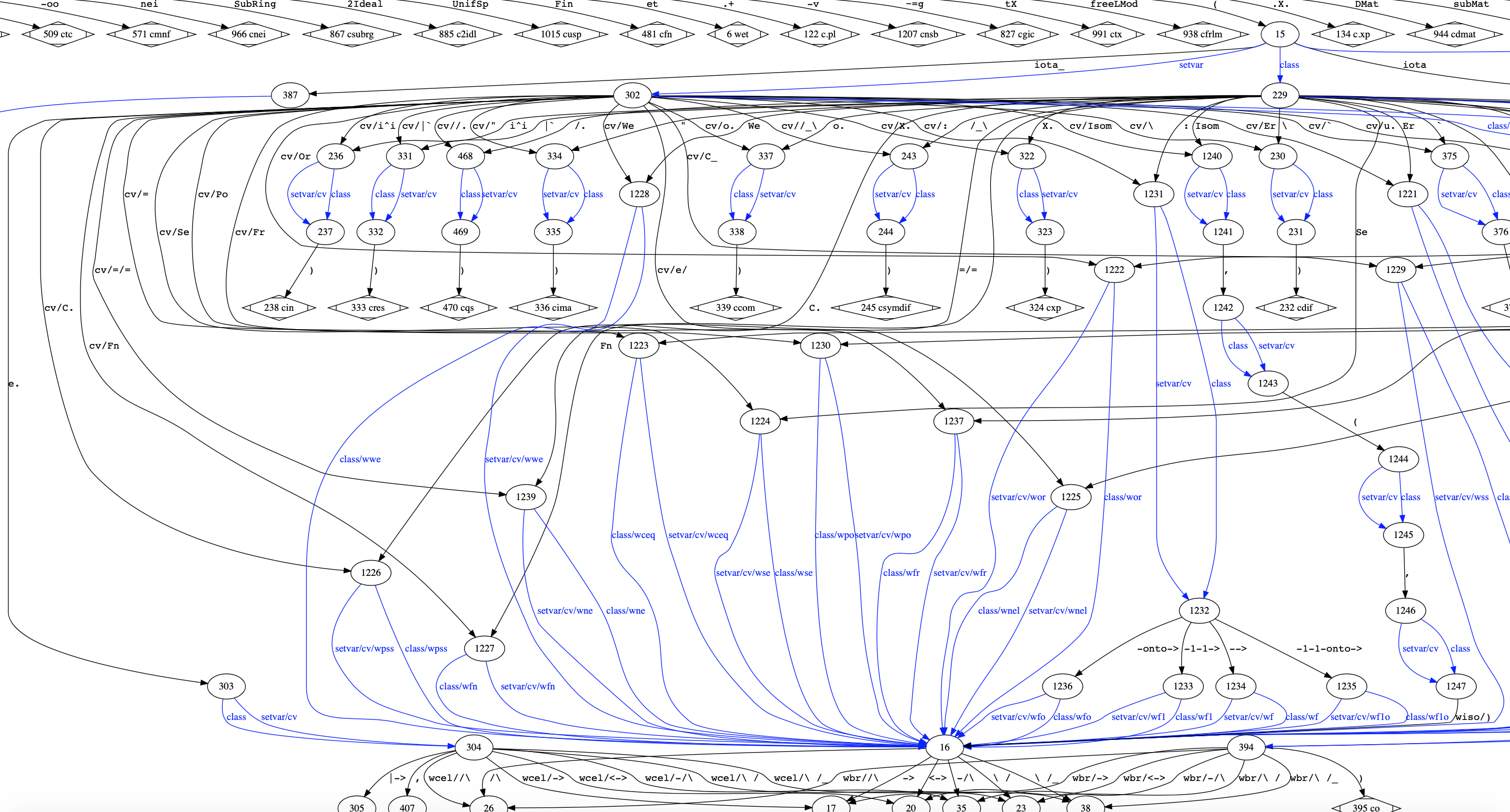
Before the actual parsing can start, the program builds a grammar
from the syntax axioms. This Grammar is a tree, and I've recently
added a function to export this tree and to visualize it using
GraphViz. I find this is probably an interesting byproduct to
share, I don't think I've seen any such thing before.
The grammar building deals with several kinds of ambiguities, and
I now understand how hard Mel O'Cat's fight must have been!
As for a simple example, here is the part of the grammar used to describe ~ wex (` E. x ph `) and ~ wrex (` E. x e. A ph `) :
This is to be interpreted as:
When encountering the ` E. ` token, move to state 86. Then, parse a setvar, and move to state 87. From there, either parse a wff, perform a ~ wex reduce and stop, or expect a ` e. ` token and move to state 87.
In state 87, if a setvar is parsed, first a ~ cv reduce shall be performed (this transforms the setvar into a class).
And so on until ~ wrex is completely parsed.
The full tree is very big, and in some cases very complex, however, once it is built, parsing can be done by "just" following it like a recipe.
You can browse the full graph here: http://metamath.tirix.org/grammar.svg
I've also uploaded the source DOT file here: http://metamath.tirix.org/grammar.dot.
The source code for this project is still at https://github.com/tirix/metamath-knife/tree/grammar.
BR,
_
Thierry
PS. Another snapshot for fun:
Here between states 1239 and 16, the automaton has read ` ( A =/= x ` , and does 2 "reduce" along the way (cv and wne).