Uncomfortable with definitions as axioms ... help?

186 views
Skip to first unread message

Samuel Goto

unread,
Dec 21, 2022, 7:12:38 PM12/21/22
to Metamath
Hey all,

   As I'm looking into metamath there is something lingering that is making me uncomfortable: definitions are axioms.

   This is obviously intended and by design by the community (the book has a whole chapter about it), but I'm still uncomfortable with the justifications and consequences.

    A few irrational feelings I think I'm having:

    - I can't parse or understand df-bi trivially. What does it mean?
    - How do I know that the axioms of the definitions aren't introducing contradictions?
    - It seems that definitions aren't supposed to "extend the language", but I don't get that sentiment as I read them
    - We say "all you need is propositional and first order logic and set theory axioms" but then proceed to introduce a bunch by definitions

    I'm sure this can't be a new sentiment, since an entire chapter in the book was dedicated to it, but I was wondering if:

    (a) Does anyone have some explanation posted online that I could read to inform myself and perhaps settle my anxiety?
    (b) Is there a version of metamath and/or set.mm that don't rely on definitions as axioms?

    Terribly sorry if this was discussed multiple times (it must have), but a quick search in this mailing list didn't match any obvious prior discussion, so apologies if I missed some.

    Sam

Mario Carneiro

unread,
Dec 21, 2022, 7:57:14 PM12/21/22
to meta...@googlegroups.com
On Wed, Dec 21, 2022 at 7:12 PM Samuel Goto <samue...@gmail.com> wrote:
Hey all,

   As I'm looking into metamath there is something lingering that is making me uncomfortable: definitions are axioms.

   This is obviously intended and by design by the community (the book has a whole chapter about it), but I'm still uncomfortable with the justifications and consequences.

You are right to be concerned. I was also concerned several years ago, and the solution I came up with was to observe that definitions in set.mm follow a very regular structure, such that all definitions with that structure can be given a metatheoretic argument for conservative extension. So I added a "definition checker" module to mmj2, which checks the rules described in the "Additional rules for definitions" section of https://us.metamath.org/mpeuni/conventions.html . This program is run as part of the set.mm CI, so we can be sure that (with a small list of exceptions) every df-* axiom is actually conservative over the ZFC axioms.
 
    A few irrational feelings I think I'm having:

    - I can't parse or understand df-bi trivially. What does it mean?

df-bi is one of the exceptions, because the first rule is that a definition has to have <-> or = as the root symbol and this doesn't work when we are defining <-> itself. That doesn't mean that the definition is not conservative, only that it can't be automatically checked. The way to read df-bi is that it is defining (𝜑 ↔ 𝜓) to be ¬ ((𝜑 → 𝜓) → ¬ (𝜓 → 𝜑)) (that is dfbi1), except that the root ↔ in the definition is itself expanded according to this expression. The justification that this is a conservative extension is that if you replace all instances of (𝜑 ↔ 𝜓) with ¬ ((𝜑 → 𝜓) → ¬ (𝜓 → 𝜑)) in df-bi, you get bijust, which is provable without df-bi. So you can perform that replacement in any derivation to eliminate the defined symbol.
 
    - How do I know that the axioms of the definitions aren't introducing contradictions?

As I mentioned, we can reduce the problem to a small list of exceptions like df-bi, plus the definition schema given by the definition checker's rules. The schema can be proved by a direct substitution argument like the one I just gave for df-bi, except that to handle bound variables we also need to have the ability to perform alpha-renaming, such as in _V = { x | x = x }, which you can use to prove the theorem { x |  x = x } = { y | y = y }, so we need to know that this was already provable before (this is vjust). The ability to perform alpha renaming in any formula is a metatheorem of set.mm's axiom system.
 
    - It seems that definitions aren't supposed to "extend the language", but I don't get that sentiment as I read them

I'm not sure I would say that. Definitions definitely are intended to extend the language, but a conservative extension means that no statements expressible in the original language become provable as a result of the introduction of the definition. (In particular, if |- F. was not provable before, it is still not provable, so the extension is sound.)
 
    - We say "all you need is propositional and first order logic and set theory axioms" but then proceed to introduce a bunch by definitions

Yes, I tend to agree with this sentiment. It's not *really* true that you don't need definitions. You don't need them *in principle*, but if you don't like exponentially long proofs (which can make a qualitative difference if you have ultrafinitist tendencies and don't trust proofs that cannot be checked on any computer present or future) then you are more or less forced to accept them.
 
    I'm sure this can't be a new sentiment, since an entire chapter in the book was dedicated to it, but I was wondering if:

    (a) Does anyone have some explanation posted online that I could read to inform myself and perhaps settle my anxiety?
    (b) Is there a version of metamath and/or set.mm that don't rely on definitions as axioms?

For the reasons I stated above, a set.mm without definitions would not be remotely usable. And metamath doesn't really support definitions in any other way.

Even with the definition checker, the situation was still somewhat problematic to me, since the definition checker is now essentially a part of the "trusted code base" of metamath (unless you want to personally review all of those thousand definitions-as-axioms in set.mm) and yet it is not a required part of metamath verifier operation, and it has only one implementation, which moreover is tailored to set.mm notions. So I tried to make a version of metamath that includes definitions as part of the kernel, and the result is Metamath Zero (https://github.com/digama0/mm0). It unfortunately complicates several things to take definitions as primitive because you need to have a notion of bound variable to handle examples like df-v, as well as a conversion judgment to handle definition unfolding without having to also bake in an equality operator (since not all metamath databases have one, or only have one for some sorts and not others). You can read about MM0 in https://arxiv.org/abs/1910.10703 .
 
Another Metamath variant which adds definitions as a primitive part of the language is GHilbert by Raph Levien, although this diverges a bit more from metamath and is closer to lambda calculus / LF in terms of its primitive operators.

Marshall Stoner

unread,
Jul 8, 2023, 5:22:17 PM7/8/23
to Metamath
I'm currently working on a "textbook-like" introduction to the system used in set.mm.  I'm currently thinking about how I should provide a proof justifying the definition of  '↔'.

I write the abbreviation eq(𝜑, 𝜓)  ≔  ¬ ((𝜑 → 𝜓) → ¬ (𝜓 → 𝜑)).  Then the definition is just the expansion of eq((𝜑 ↔ 𝜓), eq(𝜑, 𝜓)).  The elimination rule becomes (𝜑 ↔ 𝜓)  ≔  eq(𝜑, 𝜓).  Applying the elimination rule to the definition you get eq(eq(𝜑, 𝜓), eq(𝜑, 𝜓)) which can be proved as a theorem without any reference to the symbol '↔'.  Any theorem containing '↔' must have a proof tree that can be traced backwards to a statement of the definition itself.  You replace (𝜑 ↔ 𝜓) with eq(𝜑, 𝜓) in the definition, you have a proved a theorem.  You then replace it everywhere else you see it, tracing the same steps forward as you traced backwards.  Every line along along the way should still be justified since  eq(𝜑, 𝜓) is a WFF that is self-contained.

Anyways, I'm still working on the exact wording to make this "meta-argument" absolutely 100% clear to myself and anyone else.  Writing out a formal induction meta-proof in the way the standard deduction theorem is typically proved feels a bit cumbersome to me, but I don't want to just handwave anything away either.  I feel like I should maybe provide an example showing how the elimination rule would work on a WFF containing nested  '↔'.  The elimination rule has to be applied recursively until the symbol is gone.

Marshall Stoner

unread,
Jul 8, 2023, 5:40:22 PM7/8/23
to Metamath
New link.

Discher, Samiro

unread,
Jul 10, 2023, 12:48:41 PM7/10/23
to meta...@googlegroups.com

I was also disturbed by the issue of definitions being extra axioms according to Metamath, and solved it via interpreting only 'not' and 'imply' as part of the propositional core language, and all the other junctors as different ways to express something in terms of 'not' and 'imply' (which is also done in https://us.metamath.org/mmsolitaire/pmproofs.txt when proving statements which contain different junctors, see "Result of Proof" lines which differ from their theorems).

The concept to build only on what is essentially required leads to much slimmer definitions that make use of a logical system (e.g. when defining semantics).


Here is one of my exemplary syntax definitions:


Alias step verifications can be done by converting both formulas into the core language and checking for equality.

Based on


(A1) ⊢\psi\imply(\phi\imply\psi)

(A2) ⊢\psi\imply(\phi\imply\chi)\imply((\psi\imply\phi)\imply(\psi\imply\chi))
(A3) ⊢\not\phi\imply\not\psi\imply(\psi\imply\phi)
(MP) {\psi,\psi\imply\phi}⊢\phi

I gave the below proof of df-bi. Most of it proves that a formula is equivalent to itself, from where a single alias step leads to df-bi.
Since df-bi, under the previous alias definitions, equals (\phi\equiv\psi)\equiv(\phi\equiv\psi).

a2i:
1. \phi\imply(\psi\imply\chi)                                              premise
2. \phi\imply(\psi\imply\chi)\imply(\phi\imply\psi\imply(\phi\imply\chi))  (A2) ; 〈\phi, \psi〉, 〈\psi, \phi〉
3. \phi\imply\psi\imply(\phi\imply\chi)                                    (MP):1,2

mms-H6:
1. \not1\imply\not2\imply(2\imply1)                                                                     (A3) ; 〈\phi, 1〉, 〈\psi, 2〉
2. \not1\imply\not2\imply(2\imply1)\imply(0\imply(\not1\imply\not2\imply(2\imply1)))                    (A1) ; 〈\phi, 0〉, 〈\psi, \not1\imply\not2\imply(2\imply1)〉
3. 0\imply(\not1\imply\not2\imply(2\imply1))                                                            (MP):1,2
4. 0\imply(\not1\imply\not2\imply(2\imply1))\imply(0\imply(\not1\imply\not2)\imply(0\imply(2\imply1)))  (A2) ; 〈\chi, 2\imply1〉, 〈\phi, \not1\imply\not2〉, 〈\psi, 0〉
5. 0\imply(\not1\imply\not2)\imply(0\imply(2\imply1))                                                   (MP):3,4

mms-T13:
1. \not\not0\imply(1\imply\not\not0)                                                                                     (A1) ; 〈\phi, 1〉, 〈\psi, \not\not0〉
2. \not\not0\imply(\not\not(1\imply\not\not0)\imply\not\not0)                                                            (A1) ; 〈\phi, \not\not(1\imply\not\not0)〉, 〈\psi, \not\not0〉
3. \not\not0\imply(\not\not(1\imply\not\not0)\imply\not\not0)\imply(\not\not0\imply(\not0\imply\not(1\imply\not\not0)))  (mms-H6) ; 5 ; 〈0, \not\not0〉, 〈1, \not(1\imply\not\not0)〉, 〈2, \not0〉
4. \not\not0\imply(\not0\imply\not(1\imply\not\not0))                                                                    (MP):2,3
5. \not\not0\imply(\not0\imply\not(1\imply\not\not0))\imply(\not\not0\imply(1\imply\not\not0\imply0))                    (mms-H6) ; 5 ; 〈0, \not\not0〉, 〈1, 0〉, 〈2, 1\imply\not\not0〉
6. \not\not0\imply(1\imply\not\not0\imply0)                                                                              (MP):4,5
7. \not\not0\imply(1\imply\not\not0\imply0)\imply(\not\not0\imply(1\imply\not\not0)\imply(\not\not0\imply0))             (A2) ; 〈\chi, 0〉, 〈\phi, 1\imply\not\not0〉, 〈\psi, \not\not0〉
8. \not\not0\imply(1\imply\not\not0)\imply(\not\not0\imply0)                                                             (MP):6,7
9. \not\not0\imply0                                                                                                      (MP):1,8

mpd:
1. \phi\imply\psi                        premise
2. \phi\imply(\psi\imply\chi)            premise
3. \phi\imply\psi\imply(\phi\imply\chi)  (a2i):2 ; 3
4. \phi\imply\chi                        (MP):1,3

id:
1. \phi\imply(\phi\imply\phi)            (A1) ; 〈\psi, \phi〉
2. \phi\imply(\phi\imply\phi\imply\phi)  (A1) ; 〈\phi, \phi\imply\phi〉, 〈\psi, \phi〉
3. \phi\imply\phi                        (mpd):1,2 ; 4 ; 〈\chi, \phi〉, 〈\psi, \phi\imply\phi〉

mms-T35:
1. \not\not(0\imply1)\imply(0\imply1)                                                                    (mms-T13) ; 9 ; 〈0, 0\imply1〉
2. \not\not(0\imply1)\imply(0\imply1)\imply(\not\not(0\imply1)\imply0\imply(\not\not(0\imply1)\imply1))  (A2) ; 〈\chi, 1〉, 〈\phi, 0〉, 〈\psi, \not\not(0\imply1)〉
3. \not\not(0\imply1)\imply0\imply(\not\not(0\imply1)\imply1)                                            (MP):1,2

mms-*4.2:
1. P\implyP                                                                                                                  (id) ; 3 ; 〈\phi, P〉
2. P\implyP\imply(\not\not(P\implyP\imply\not(P\implyP))\imply(P\implyP))                                                    (A1) ; 〈\phi, \not\not(P\implyP\imply\not(P\implyP))〉, 〈\psi, P\implyP〉
3. \not\not(P\implyP\imply\not(P\implyP))\imply(P\implyP)                                                                    (MP):1,2
4. \not\not(P\implyP\imply\not(P\implyP))\imply(P\implyP)\imply(\not\not(P\implyP\imply\not(P\implyP))\imply\not(P\implyP))  (mms-T35) ; 3 ; 〈0, P\implyP〉, 〈1, \not(P\implyP)〉
5. \not\not(P\implyP\imply\not(P\implyP))\imply\not(P\implyP)                                                                (MP):3,4
6. \not\not(P\implyP\imply\not(P\implyP))\imply\not(P\implyP)\imply(P\implyP\imply\not(P\implyP\imply\not(P\implyP)))        (A3) ; 〈\phi, \not(P\implyP\imply\not(P\implyP))〉, 〈\psi, P\implyP〉
7. P\implyP\imply\not(P\implyP\imply\not(P\implyP))                                                                          (MP):5,6
8. \not(P\implyP\imply\not(P\implyP))                                                                                        (MP):1,7
9. P\equivP                                                                                                                  alias:8

df-bi:
1. \phi\equiv\psi\equiv(\phi\equiv\psi)                                                                                                                              (mms-*4.2) ; 9 ; 〈P, \phi\equiv\psi〉
2. \not(((\phi\equiv\psi)\imply\not((\phi\imply\psi)\imply\not(\psi\imply\phi)))\imply\not(\not((\phi\imply\psi)\imply\not(\psi\imply\phi))\imply(\phi\equiv\psi)))  alias:1

Here is a way to define these formal proofs:

Reasons and alias steps are technically not even part of a formal proof, but they should in practice be provided for clarity.
Depending on the alias step, one might even prefer several sub-steps because it can be a little too much for our sluggish minds to process.
However, the theory is nice and clean this way, which I think was the focus here.

Von: meta...@googlegroups.com <meta...@googlegroups.com> im Auftrag von Marshall Stoner <mbsto...@gmail.com>
Gesendet: Samstag, 8. Juli 2023 23:40:22
An: Metamath
Betreff: Re: [Metamath] Uncomfortable with definitions as axioms ... help?
 
--
You received this message because you are subscribed to the Google Groups "Metamath" group.
To unsubscribe from this group and stop receiving emails from it, send an email to metamath+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/metamath/a3d5056d-9e16-4678-af16-1a91431bbffcn%40googlegroups.com.

Marshall Stoner

unread,
Jul 11, 2023, 10:35:52 PM7/11/23
to Metamath
I trust that intuitively that these definitions are valid.  The problem is an alias rule can still fail if the syntax of the definition doesn't meet certain criteria.  If the parenthesis surrounding ↔ were missing in the definition of the biconditional, for instance.  If I could understand how the definition checker for the set.mm database works I would have a better understanding.  I have my own hypothesis, but I'm not sure if it's fully sufficient.

My hypothesis would as follows...

Let  LS⁺ᴰ is the set of all WFFs in the system with new definition D and LS is the set of all WFFs in the system before adding the new definition.  Then let F ≔ { Ψ ⇒ Φ } be the substitution rule replacing the definiendum Ψ with the definiens Φ.  

Now the first criteria should be that for any member of LS⁺ᴰ, a member of LS should result after applying F a finite number of times.

The second criteria is that if we call the process of applying F a finite number of times to obtain a member of LS, F*, then F* should be a function.  I.e. the result should be unique.  If in any case the result depends on the order application (ambiguous nesting of the definiendum or clashing with other symbols), then the definition is going to be creative.

But are these two criteria alone enough?

Mario Carneiro

unread,
Jul 12, 2023, 12:02:45 AM7/12/23
to meta...@googlegroups.com
On Wed, Jul 12, 2023 at 4:35 AM Marshall Stoner <mbsto...@gmail.com> wrote:
I trust that intuitively that these definitions are valid.  The problem is an alias rule can still fail if the syntax of the definition doesn't meet certain criteria.  If the parenthesis surrounding ↔ were missing in the definition of the biconditional, for instance.  If I could understand how the definition checker for the set.mm database works I would have a better understanding.  I have my own hypothesis, but I'm not sure if it's fully sufficient.

That example fails for a very simple reason: it wouldn't parse. Step 0 of the definition checker is to parse the definition as a wff, and if you omit the parentheses then the parser would fail on this axiom. This would actually cause mmj2 to fail if you wrote a non-parsing statement anywhere, not just in a definition but in any $e, $a, or $p statement.

If you changed the definition of the syntax "ph ↔ ps" itself to not have parentheses, and removed it from the definition as well, then it would parse, but mmj2 would still fail for a different parsing reason: the resulting grammar is ambiguous and the parser constructs some tables that witness unambiguity of the grammar, meaning that this parser construction will fail if the grammar is ambiguous.

In both cases it isn't really the definition checker catching the error. The definition checker presupposes that the database has an unambiguous grammar and all statements parse by that grammar.

Discher, Samiro

unread,
Jul 12, 2023, 12:13:34 AM7/12/23
to Metamath

"The problem is an alias rule can still fail if the syntax of the definition doesn't meet certain criteria. [...]"

Maybe I should've been clearer about the syntax definition. In my theory, one can skip a lot of parentheses since I considered left first bracketing, which I explained prior to that definition. Metamath however enforces formulas of a style with fixed parentheses and would thereby deny any input where formulas omit or introduce those.


Formulas are actually tree structures, for example the theorem of df-bi has the following syntax tree:



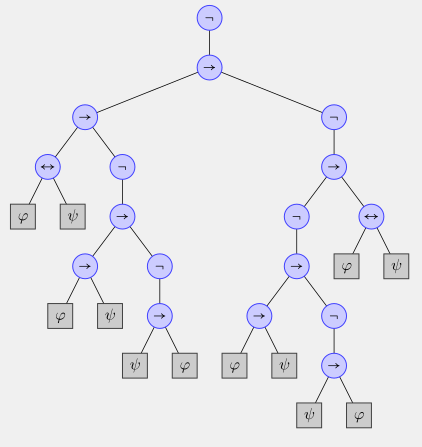
You could put parentheses around formulas in infinitely many correct ways, while not changing the identity of the formula. That has nothing to do with intuition, but is well-defined based on bracketing order, as well as order of order of precedence for operators (but in this case, all binary operators share the same priority, and it doesn't matter for nullary and unary operators).

Parentheses in logic work just the same as in all kinds of mathematical formulas, they merely prescribe order of operation. Some kind of solvers (such as Metamath) rule this out for efficiency or ease of implementation, but that is a technical detail that is rather disruptive and inelegant in a theoretical context.


All the alias replacement rules are well defined, regardless of which parentheses were used. If the parentheses change in the way that the identity of the formula (here: the order of operations) changes, the corresponding rules simply do not apply anymore.


My solution was merely meant to answer your questions on how df-bi can be justified via a rigorous proof from Metamath's propositional axioms. I have no better understanding in how Metamath's "definition checker" works than definitions being treated merely as axioms, as has been confirmed by multiple people in this thread.

Additionally, I understand that these definitions are well-justified, which is also pointed out, for example, in the description of df-bi ( see https://us.metamath.org/mpeuni/df-bi.html ).

I have provided you with a proof for that.


Gesendet: Mittwoch, 12. Juli 2023 04:35:51

Marshall Stoner

unread,
Jul 12, 2023, 2:53:49 AM7/12/23
to Metamath
I wasn't talking about set.mm or mmj2.  I was talking in metamath in general, which doesn't seem to enforce non-ambiguity since it only reads strings of tokens with no other underlying structure.  I was in learning the definition checker rules in terms of learning in detail how definitions are theoretically justified.   I didn't know there was a parsing step in mmj2 separate from metamath itself, so I assumed it was part of the definition checker (since theorem grammar is taken care of by 'w' axioms during proof verification).

Marshall Stoner

unread,
Jul 12, 2023, 4:01:41 AM7/12/23
to Metamath
Sorry I didn't have time to read the proof you shared.  I couldn't read it easily and wasn't sure if it completely answered what I really wanted since I want to show that definitions satisfy the precise meaning of eliminability and non-creativity.  Maybe the proofs help but I couldn't convert them to something I could actually read like latex or unicode.  Sorry, reading that format just hurts my eyes.


There seems to be some steps missing because nothing inside the formal language can alone prove a metalogical fact.  It's a meta-theorem like the deduction theorem that seems intuitively trivial still needs some kind of inductive proof.

Mario Carneiro

unread,
Jul 12, 2023, 5:30:38 AM7/12/23
to meta...@googlegroups.com
The justification of definitions requires imposing additional structure on metamath databases in the form of being able to unambiguously parse statements into trees. Without it, you can't use the definition checker at all, and the rules do not make sense / could be circumvented without more rules.

--
You received this message because you are subscribed to the Google Groups "Metamath" group.
To unsubscribe from this group and stop receiving emails from it, send an email to metamath+u...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/metamath/1c92e482-fcee-4659-a858-076edb89d6e5n%40googlegroups.com.

Discher, Samiro

unread,
Jul 12, 2023, 10:11:15 AM7/12/23
to meta...@googlegroups.com
"I couldn't convert them to something I could actually read like latex or unicode"

The proof format is meant to allow readability by both machines (easy and flexible when able to code) and humans (in a text editor without word wrapping).

Apart from some missing spaces, these formulas are in LaTeX format, and reasons are nicely indented for text editors.
You could simply use
 \def\not{\lnot}
 \def\equiv{\leftrightarrow}
 \def\imply{\rightarrow}
 \def\phi{\varphi}
in the .tex file and insert spaces when [a-zA-Z] rather than [0-9] follows a command via regex-search-and-replace. More seach-and-replace can put it into any desired LaTeX commands.

If you have issues reading LaTeX-formatted formulas, you can also use search and replace to convert it to unicode, e.g. replace all "\imply" by "→", all "\phi" by "φ", and so on.

I used my own converter on my example, which makes some explicit information (like substitutions and referenced line numbers - useful for programs) implicit, but makes it even easier to read as a human. I am sending the resulting .tex file.
Here is what it looks like when parsed: https://i.imgur.com/a31LACW.png

Hope this helps.

Gesendet: Mittwoch, 12. Juli 2023 10:01:41
df-bi_summary.tex

Marshall Stoner

unread,
Jul 12, 2023, 7:16:35 PM7/12/23
to Metamath

Thanks.  I got it.  I'm rusty with LaTex and forgot about redefinition commands.  It was late when I looked so I gave up when I got errors.

It is what I thought it was.  I have proved line 8 of 4.2 in a different way from other results.  I wrote it as...
⊢ eq( φ  ,φ ) where I define eq( phi , psi ) ≔ ¬ ( ( φ → ψ ) → ¬ ( ψ → φ ) ).

I also have " ⊢ eq( φ , ψ ) →  ( φ → ψ ) ",  " ⊢ eq( φ , ψ ) → ( ψ → φ ) ",  and " ⊢ ( φ → ψ ) → ( ( ψ → φ ) →  eq( φ , ψ ) ) " written up with proofs.

I realize eq( φ , ψ ) is exactly the same as φ ↔ ψ in the practical sense, but without alias capability, metamath needs to use eq( φ ↔ ψ , eq( φ , ψ ) ) instead since the literal '↔' can only be used with later definitions.

I really should have started a new topic as I confused everyone by reviving an old discussion with a different question as OP.  I was more interested in how to formally state and prove the generalized case where I can show any definition with certain criteria satisfies the precise definition of being eliminable and non-creative/conservative as in...


A rigorous proof shouldn't be hard for purely propositional statements, but predicate logic is much more tricky with free variable clashes and certain definitions that require auxiliary existence and uniqueness theorems as justification in order to satisfy the eliminability and non-creativity properties. 

Maybe someone could point me in the direction of a formal 1st order logic text that covers these topics.  I have a textbook, but this particular topic is not covered.  I will possibly buy another text but want to make sure all topics I'm interested in are covered first.  I was just thinking maybe I could dig something up online in the meantime.

Thanks.

Discher, Samiro

unread,
Jul 12, 2023, 9:29:43 PM7/12/23
to Metamath

According to
https://math.stackexchange.com/questions/1123312/theory-of-definitions,
(referencing the same book as the question you mentioned) these properties are required by all definitions, and there are also some criteria listed and explained for a certain type of definition. Maybe this is a lead in the right direction?


I wonder how useful the ability to use aliases instead of axiomatic definitions is in detecting those properties as well, but given that I invented aliases myself and haven't seen them in any textbook, I don't know of anyone who studied this and, if so, how they called it.


Gesendet: Donnerstag, 13. Juli 2023 01:16:34
Reply all
Reply to author
Forward
0 new messages