The magic of the number 14?
Linda Fahlberg-Stojanovska
Hiya all,
I was just thinking about how the books go on and on about teaching our kids that if we
==double the side of a square, the area is quadrupled==
I realized that no one ever says “double the diameter of a circle, ….” so plan 1 is to see if I can create a visualization with geogebra about this. (Anybody got one already?) I presume 8 wedges will be double in height and double in length… http://www.geogebratube.org/student/m111
Magic of 14.
I also realized that nobody ever says the much more useful:
“What number times the side/diameter gives double the area?”
I presume this is because “officially” you need sqrt(2). But 1.4^2=1.96 or almost 2.
Suppose a 10” pizza costs $10 and a 14” pizza costs $18. Should you but two 10” pizzas or one 14” pizza?
(While I was in this problem – I thought to myself: Maybe you get more/less crust … Do you?)
Of course, I only “know” the times tables up to 12. What a pity. 14 is the magic number that gets you (almost) double the area. So if we knew the 14 times table:
· We could check when an 8”pizza was doubled in size. (Answer: 11.2”)
· Or when an image will be half the filesize: (1.4/2=70%) (This is why engineers say: sin(45 degrees)=0.7 or 0.707)
Conclusion: I think the number 14 deserves a lot more of our time :)
Warm regards to all, Linda
Maria Droujkova
Hiya all,
I was just thinking about how the books go on and on about teaching our kids that if we
==double the side of a square, the area is quadrupled==
I realized that no one ever says “double the diameter of a circle, ….” so plan 1 is to see if I can create a visualization with geogebra about this. (Anybody got one already?) I presume 8 wedges will be double in height and double in length… http://www.geogebratube.org/student/m111
Dr. Maria Droujkova
Alexander Bogomolny
--
You received this message because you are subscribed to the Google Groups "MathFuture" group.
To unsubscribe from this group and stop receiving emails from it, send an email to mathfuture+...@googlegroups.com.
To post to this group, send email to mathf...@googlegroups.com.
Visit this group at http://groups.google.com/group/mathfuture?hl=en.
For more options, visit https://groups.google.com/groups/opt_out.
Linda Fahlberg-Stojanovska
Thanks Alex. I knew you would have applets and information :). As always I appreciate your reply! Thank-you Maria too!
I did manage to make the an easy applet to show double the radius, quadruple the area: http://www.geogebratube.org/student/m29088
I could not for the life of me (or at least 5 hours of me) figure out how to map the ring that sticks out from a 14” pizza into a 10” pizza (since they have the same area). It was interesting to realize that two “opposing” irrational numbers are at play: pi and sqrt(2).
Best, Linda
P.S. This was cool to see in Alex’s pizza applet (The blue is half the red.):
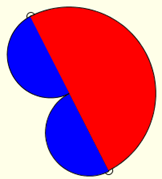
Alexander Bogomolny
Juan
About 14, yes, its square is 196, and you can get 196 by swapping the last two digits of 169, which is the square of 13. It's just a mnemonic trick.
The calculation 14x14 = 13x15 + 1 = 130 + 65 + 1 is not too boring, and it illustrates an example of the difference-of-two-squares algebra formula.
Also, after 1.4 in sqrt(2), the next two digits give you another 14, because sqrt(2) = 1.414...
In relation to Boolean algebra, truth tables, and Boolean functions, there is a natural labeling / indexing / one-to-one correspondence between the set of non-negative integers, and the set of all Boolean functions of a finite number of variables, where you can consider the set of all Boolean functions on n variables, just as an extension of all the Boolean functions of n-1 variables. Now, under these assumptions:
1) As binary digits, 0='false' and 1='true'
2) The number 0 always represents the constant Boolean function "False," for any number of input variables
3) The constant function "True" (constant for the first n input variables only) is represented by the number 2^(2^n) - 1
Then the number 14 seen as a Boolean function on two input Boolean variables P and Q,
is the function given by the truth-table of the logical connective OR (inclusive 'or').
So in functional notation you could say 14(P,Q) = "P or Q"
while, as an infix operator it would be (P 14 Q) = "P or Q"
Given that the constant Boolean function "True" for two variables, is represented by the number 15, you could say that, in the limited universe of two-argument logical operators, the number 14 is up there right next to the truth :-)
Juan
On Saturday, February 2, 2013 3:45:36 AM UTC-8, LFS wrote:
Magic of 14.I also realized that nobody ever says the much more useful:
“What number times the side/diameter gives double the area?”
I presume this is because “officially” you need sqrt(2). But 1.4^2=1.96 or almost 2.
Of course, I only “know” the times tables up to 12. What a pity. 14 is the magic number that gets you (almost) double the area.
Conclusion: I think the number 14 deserves a lot more of our time :)
John Mason
that the area swept out by a moving segment which never overlaps itself
is the length of the segment times the length of curve traced out by the
midpoint of the segment? (Imagine an animation that shows only a few of
the segment positions).
JohnM
On 02/02/2013 23:03, Alexander Bogomolny wrote:
> Linda, hi. You created a wonderful applet - I have yet to digest the idea
> that GeoGebra allows such versatility.
>
> Mapping a ring to a circle makes use of a different idea - sweeping.
>
> http://www.cut-the-knot.org/Curriculum/Geometry/PythFromRing.shtml
>
> The difference is like that between indivisibles and infinitesimals. There
> are several relevant articles by Apostol & Mamikon (two mentioned on the
> page just linked to). They I believe have just published a book that sums
> up their cooperation of several years - mostly this subject or getting
> calculus facts geometrically.
>
> Another possibility is to use similarity. Inscribe a circle into a square.
> That's pretty intuitive that ratio of the area of the circle to the
> left-over area does not depend of the size of the square - why should it?
> If so, each changes at the same rate as the square (when the side of the
> square changes).
>
> With best wishes,
>
> Alex
>
>
> On Sat, Feb 2, 2013 at 5:13 PM, Linda Fahlberg-Stojanovska <
> lfah...@gmail.com> wrote:
>
>> Thanks Alex. I knew you would have applets and information :). As always I
>>
>> ** **
>> I did manage to make the an easy applet to show double the radius,
>>
>> ** **
>> I could not for the life of me (or at least 5 hours of me) figure out how
>> they have the same area). It was interesting to realize that two �opposing�
>> irrational numbers are at play: pi and sqrt(2).****
>>
>> ** **
>>
>> Best, Linda****
>>
>> P.S. This was cool to see in Alex�s pizza applet (The blue is half the
>> red.): ****
>>
>> ****
>>
>> ** **
>>
>> *From:* mathf...@googlegroups.com [mailto:mathf...@googlegroups.com] *On
>> Behalf Of *Alexander Bogomolny
>> *Sent:* Saturday, February 02, 2013 1:48 PM
>> *To:* mathf...@googlegroups.com
>> *Subject:* Re: [Math 2.0] The magic of the number 14?****
>>
>> ** **
>>
>> If the kids hae an idea of the Pythagorean theorem then****
>>
>> ** **
>>
>> 1) there are optimization problems related to pizza sizes ****
>>
>> ** **
>>
>> http://www.cut-the-knot.org/Curriculum/Geometry/Pizza.shtml****
>>
>> ** **
>> 2) along with the circle, the ring, has its area dependent on a single
>> parameter: the tangent to the inner circle inside the big circle. So it's
>> nice to verify that when the radius of the circles doubles it produces a
>>
>> ** **
>>
>> http://www.cut-the-knot.org/pythagoras/corollary.shtml#ring****
>>
>> ** **
>>
>> Alex****
>>
>> ** **
>> wrote:****
>>
>> Wow, neat application about pizzas!!! Love it!****
>>
>> ** **
>>
>> ** **
>> On Sat, Feb 2, 2013 at 6:45 AM, Linda Fahlberg-Stojanovska <
>>
>> Hiya all, ****
>>
>> ****
>> I was just thinking about how the books go on and on about teaching our
>>
>> ==double the side of a square, the area is quadrupled==****
>>
>> ****
>>
>> I realized that no one ever says �double the diameter of a circle, �.� so
>> (Anybody got one already?) I presume 8 wedges will be double in height and
>>
>> ** **
>> Well, physics and engineering people talk about that stuff. The
>> conversation goes like, "This quantity changes as the second (third,
>>
>> ** **
>> For example, the position in free fall on a planet changes as the square
>> of time. The area changes as the square of linear measures - WHATEVER 2d
>>
>> ** **
>> The most recent conversation we had about that with kids ended up at
>> something like, "And if the diameter of your four-dimensional watermelon
>>
>> ** **
>>
>> ** **
>>
>> Cheers,
>> Dr. Maria Droujkova****
>>
>> 919-388-1721 ****
>> --
>> You received this message because you are subscribed to the Google Groups
>> "MathFuture" group.
>> To unsubscribe from this group and stop receiving emails from it, send an
>> email to mathfuture+...@googlegroups.com.
>> To post to this group, send email to mathf...@googlegroups.com.
>> Visit this group at http://groups.google.com/group/mathfuture?hl=en.
>> For more options, visit https://groups.google.com/groups/opt_out.
>>
>>
>> ** **
>> --
>> You received this message because you are subscribed to the Google Groups
>> "MathFuture" group.
>> To unsubscribe from this group and stop receiving emails from it, send an
>> email to mathfuture+...@googlegroups.com.
>> To post to this group, send email to mathf...@googlegroups.com.
>> Visit this group at http://groups.google.com/group/mathfuture?hl=en.
>> For more options, visit https://groups.google.com/groups/opt_out.
>>
John Mason
http://demonstrations.wolfram.com/MamikonsProofOfThePythagoreanTheorem/
for a proof of Pythagoras using sweeping tangents (I think appealing to
Pappus' theorem underneath perhaps?)
JohnM
On 02/02/2013 23:03, Alexander Bogomolny wrote:
> that GeoGebra allows such versatility.
>
> Mapping a ring to a circle makes use of a different idea - sweeping.
>
> http://www.cut-the-knot.org/Curriculum/Geometry/PythFromRing.shtml
>
> The difference is like that between indivisibles and infinitesimals. There
> are several relevant articles by Apostol & Mamikon (two mentioned on the
> page just linked to). They I believe have just published a book that sums
> up their cooperation of several years - mostly this subject or getting
> calculus facts geometrically.
>
> Another possibility is to use similarity. Inscribe a circle into a square.
> That's pretty intuitive that ratio of the area of the circle to the
> left-over area does not depend of the size of the square - why should it?
> If so, each changes at the same rate as the square (when the side of the
> square changes).
>
> With best wishes,
>
> Alex
>
>
> On Sat, Feb 2, 2013 at 5:13 PM, Linda Fahlberg-Stojanovska <
> lfah...@gmail.com> wrote:
>
>> Thanks Alex. I knew you would have applets and information :). As always I
>>
>> ** **
>> I did manage to make the an easy applet to show double the radius,
>>
>> ** **
>> I could not for the life of me (or at least 5 hours of me) figure out how
>> they have the same area). It was interesting to realize that two �opposing�
>> irrational numbers are at play: pi and sqrt(2).****
>>
>> ** **
>>
>> Best, Linda****
>>
>> P.S. This was cool to see in Alex�s pizza applet (The blue is half the
>> red.): ****
>>
>> ****
>>
>> ** **
>>
>> *From:* mathf...@googlegroups.com [mailto:mathf...@googlegroups.com] *On
>> Behalf Of *Alexander Bogomolny
>> *Sent:* Saturday, February 02, 2013 1:48 PM
>> *To:* mathf...@googlegroups.com
>> *Subject:* Re: [Math 2.0] The magic of the number 14?****
>>
>> ** **
>>
>> If the kids hae an idea of the Pythagorean theorem then****
>>
>> ** **
>>
>> 1) there are optimization problems related to pizza sizes ****
>>
>> ** **
>>
>> http://www.cut-the-knot.org/Curriculum/Geometry/Pizza.shtml****
>>
>> ** **
>>
>> parameter: the tangent to the inner circle inside the big circle. So it's
>> nice to verify that when the radius of the circles doubles it produces a
>>
>> ** **
>>
>> http://www.cut-the-knot.org/pythagoras/corollary.shtml#ring****
>>
>> ** **
>>
>> Alex****
>>
>> ** **
>>
>>
>> Wow, neat application about pizzas!!! Love it!****
>>
>> ** **
>>
>> ** **
>>
>>
>> ==double the side of a square, the area is quadrupled==****
>>
>> ****
>>
>> I realized that no one ever says �double the diameter of a circle, �.� so
>> (Anybody got one already?) I presume 8 wedges will be double in height and
>> conversation goes like, "This quantity changes as the second (third,
>>
>> ** **
>> For example, the position in free fall on a planet changes as the square
>> of time. The area changes as the square of linear measures - WHATEVER 2d
>>
>> ** **
>> The most recent conversation we had about that with kids ended up at
>> something like, "And if the diameter of your four-dimensional watermelon
>>
>> ** **
>>
>> ** **
>>
>> Cheers,
>> Dr. Maria Droujkova****
>>
>> 919-388-1721 ****
>>
>> You received this message because you are subscribed to the Google Groups
>> "MathFuture" group.
>> To unsubscribe from this group and stop receiving emails from it, send an
>> email to mathfuture+...@googlegroups.com.
>> To post to this group, send email to mathf...@googlegroups.com.
>> Visit this group at http://groups.google.com/group/mathfuture?hl=en.
>> For more options, visit https://groups.google.com/groups/opt_out.
>>
>>
>> ** **
>> --
>> You received this message because you are subscribed to the Google Groups
>> "MathFuture" group.
>> To unsubscribe from this group and stop receiving emails from it, send an
>> email to mathfuture+...@googlegroups.com.
>> To post to this group, send email to mathf...@googlegroups.com.
>> Visit this group at http://groups.google.com/group/mathfuture?hl=en.
>> For more options, visit https://groups.google.com/groups/opt_out.
>>
Linda Fahlberg-Stojanovska
Hiya!
I think I can do the sweep thing! Thanks so much Alex and Jason for the links. I will report back when I have a working applet.
Thanks Juan - that was fun to read.
Thanks to MathHombre for the tweet (and I was just adding your latest blog to my livebinder when it came in)!
>> how to map the ring that sticks out from a 14” pizza into a 10” pizza
>> (since they have the same area). It was interesting to realize that two “opposing”
>> irrational numbers are at play: pi and sqrt(2).****
>>
>> ** **
>>
>> Best, Linda****
>>
>> P.S. This was cool to see in Alex’s pizza applet (The blue is half
>> I realized that no one ever says “double the diameter of a circle,
>> ….” so plan 1 is to see if I can create a visualization with geogebra about this.
>> (Anybody got one already?) I presume 8 wedges will be double in
>> height and double in length…
Alexander Bogomolny
--
Alexander Bogomolny
 H
H--
Alexander Bogomolny
kirby urner
(polyhedron-as-wireframe) known as the cuboctahedron.
Recipe: start with an equilateral triangle, constructed however, then
build squares off each side.
Now crease the edges the triangle and squares share such that the
squares angle downward exactly enough to accommodate three more
equilateral triangles in between them. That's seven facets. That's
your hemisphere. **
Another way to look at the cuboctahedron is as four hexagons
intersecting each other like rings around a common nucleus. That
helps give a fix on the edge count: 4 * hex (4 * 6).
http://www.flickr.com/photos/obiter/5652903981/ (six frequency)
http://www.flickr.com/photos/yoyobandalore/5515575901/ (five frequency)
Yet another way to look at the cuboctahedron is in terms of uniform
spheres, say of unit radius, with twelve packed around a nuclear 13th
ball. The number of balls in a 2nd layer would be 42, and the shape
would still be cuboctahedral.
I have an animated graphic showing that here:
http://www.4dsolutions.net/ocn/xtals101.html (upper right)
http://www.flickr.com/photos/kirbyurner/4903290928/ (link to Martian math)
Kirby
** you will notice two different ways to compose the 7-faceted
hemispheres, either by having squares meet with triangles or by having
squares meet with squares. The former is the more omni-symmetric e.g.
gets the pattern around each vertex to be the same. The latter falls
out of the Archimedean set (doesn't qualify) but remains what's called
a Johnson. J27 is what some call it.
http://www.orchidpalms.com/polyhedra/johnson/johnson.html
kirby urner
show VRML files. VRML = Virtual Reality Markup Language. Not new
by this time.
There are lots of VRML files out there, and I see no reason to prevent
new generations of kids from making more of them, as they're not all
that complicated as formats go, are human readable. As you're growing
your math skills, why not tackle this mathematical topic?
http://www.georgehart.com/virtual-polyhedra/vp.html
The thing about polyhedrons is they're abstract mathematical concepts
but also literal objects, so the wish or need to visualize or hold in
a tactile sense is satisfied.
With such shapes, we get a handle on a simple topological rule, not
hard to show / prove visually (Cromwell's 'Polyhedra' has a nice one,
in prose, drawn from von Staudt): V + F = E + 2. **
But you've also got the concepts of angle (central and surface),
polygon, vector (if you want it), rotation / tranlsation / scaling,
plus polyhedral numbers (like figurate), concept of symmetry,
polarity, volume, surface, cross-sections... such a rich hub. They
even bridge to data structures, as they get to be represented in rows
and columns as well (SQL...).
<rant>
So why are polyhedrons given short shrift? (obviously in my view they are).
</rant>
Anyway http://www.instantreality.org/ is where I ended up, in my
search for a VRML viewer.
I now appear to have a decent VRML viewing solution. I'm on OS X 10.7.5.
Kirby
** and a lot more history.
The contention of 'Descartes Secret Notebook' is that this V + F = E +
2 relationship had been discovered earlier by Descartes but he was
really worried about his reputation with the church, in itself a
really complicated story. The guy ways always feeling hunted, if only
by his overly oppressive / invasive friends.
http://www.goodreads.com/book/show/208929.Descartes_s_Secret_Notebook
Linda Fahlberg-Stojanovska
Thank-you Alex for writing this. Good to know it won’t work before I work on it :). I did like the onion peel and I am glad you wrote it up and showed the fourths. Good reference. How you all keep up the energy for blogs – oh my.
Warm regards, Linda
roberto
--
Roberto
