Exponential and Logarithm Mapping on Stiefel Manifold
32 views
Skip to first unread message
Ana Hiza Ramirez-andrade
Feb 11, 2021, 3:59:18 PM2/11/21
to Manopt
Hello,
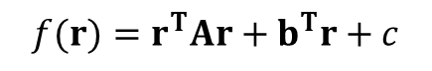
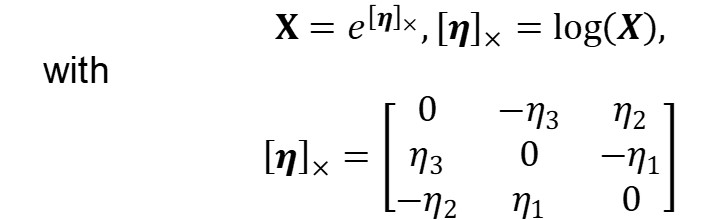
Is this the correct way to use the toolbox?
Do you have any suggestions to overcome this problem?
I've trying to use manopt to solve a cost function of the form:
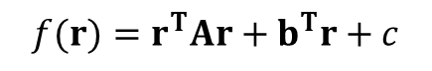
with x, the vectorization of X, an X matrix in the Stiefel Manifold. The mapping between the manifold and the tangent space is exponential.
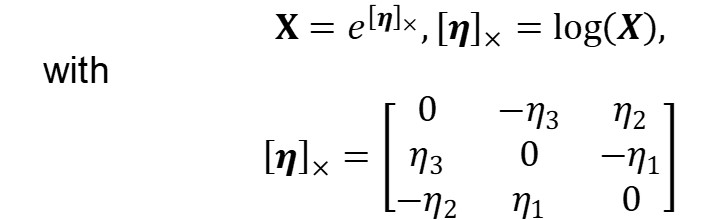
for this function, the gradient in the Stiefel Manifold is a 3x1 matrix, and the hessian is 3x3.
I tried using the next lines, but I get an error due to the size of the gradient
M = stiefelfactory(3, 3);
problem.M = M;
problem.costgrad = @(X)fandGrad(X,A,b,c);
problem.hess = @(X,u)Hessf(X,u,store);
[x_opt cost_opt info] = trustregions(problem, X0, options);
Do you have any suggestions to overcome this problem?
Thank you in advance.
Ana Ramirez
Nicolas Boumal
Feb 12, 2021, 2:04:38 AM2/12/21
to Manopt
Hello Ana,
Best,
I'm not clear on the setup. Is $r$ in $f(r)$ supposed to be $x$? Even so, I do not see what $\eta$ is. Looking at the expression for $\eta$ I'm wondering if what you actually want to optimize over is the orthogonal group?
In any case, M = stiefelmanifold(3, 3) will give you a structure M that describes the following manifold:
${ X \in R^{3 x 3} : X^T X = I_3 }$
where $I_3$ is the identity matrix of size 3 x 3.
So, points and vectors on the manifold are matrices of size 3 x 3. They are not column vectors. You can use Matlab instructions to vectorize them of course, but that is just a Matlab language issue.
Best,
Nicolas
Reply all
Reply to author
Forward
0 new messages
