Quadratic Problem with Quadratic Equality Constraints

61 views

Skip to first unread message

Li Yihui

unread,

Jun 29, 2022, 2:37:19 AM6/29/22

to Manopt

Hi, there:

I have a quadratic problem with quadratic equality constraints:

given $\mathbf{K} \in \mathbb{R}^{n \times n}$ , $\mathbf{P_{0}} \in \mathbb{R}^{n \times 3}$ , $\mathbf{M} \in \mathbb{R}^{m \times n}$ , $\mathbf{A} \in \mathbb{R}^{m \times 3}$ , $\mathbf{N} \in \mathbb{R}^{k \times n}$ , $\mathbf{L} \in \mathbb{R}^{k \times 1}$ and $m,k < n$ . We want to get $\mathbf{P}$ by solving the following optimization problem:

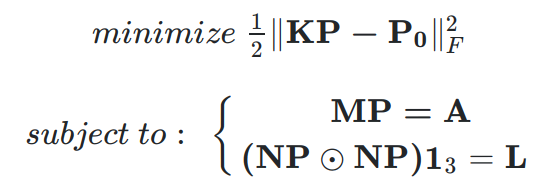
where $\mathbf{P} \in \mathbb{R}^{n \times 3}$ , $\mathbf{1}_{3}\in \mathbb{R}^{3 \times 1}$ whose entries are all 1's, $\odot$ is Hadamard product (elements-wise product).

For better reading, you can find this problem here.

I think it's a non-convex problem and those convex solver, such as CVXPY, can not handle it. I found a similar problem in StackExchange, and MANOPT is suggested to solve by Mark L. Stone. I am a fresh man in manifold and MANOPT, I would really appreciate it if someone can give me some advice about how to format the problem with MANOPT, or with other solver.

Many thanks!

Nicolas Boumal

unread,

Dec 28, 2022, 5:45:21 PM12/28/22

to Manopt

Hello,

This is an interesting problem. It doesn't fit directly in Manopt, so unfortunately I do not have a short answer to offer.

Do you have examples of matrices K, P0, M, A, N, L that you can share by any chance?

I'm thinking you could try to optimize jointly over P and X, with constraints MP = A and NP = X, and also that the rows of X have squared norms prescribed by L. Manopt could handle the latter easily with sphere constraints (obliquefactory), which could effectively leave a quadratic cost and linear constraints. The linear constraints might be easy enough to handle with an Augmented Lagrangian type of approach. But it's hard to tell if that would actually be effective without trying.

Best,

Nicolas

Reply all

Reply to author

Forward

0 new messages