PSO feasible solution checking

[Kimmy Kong]

Dear Manopt group

   I have a problem on understanding the solution by PSO solvers. 

I try to use PSO to solve 'A first example'-eigenvector dominant one, the solution 'x' should satisfy two conditions, x'*x = 1  and A*x./x = lamda *I (1 vector), 

but the PSO get a solution only satisfy x*x = 1, 

solution-it is only satisfied at critical points, that is, points where the Riemannian gradient is zero.--thank you for the reply, 

but

Is this mean that the solution found by PSO is wrong?

And can I ask where to check if a solution is feasible, I did not find the process in code. 

thank you for the code,

And also there is another question, is the solution by PSO is feasible for other problems?

thank you

  

[Ronny Bergmann]

Hi,

without example code it is a bit complicated to follow you completely, but let me try to comment a bit on your questions. With your example you refer to https://www.manopt.org/tutorial.html#firstexample ?

1. The constant x'*x = 1 is ensured by the manifold. This condition always holdes.

2.  I am not sure where you have you second condition from, nor how you would have included that into PSO. From the example you would use the implemented cost (problem.cost  = @(x) -x'*(A*x);), since PSO does not use the gradient. That also means that the “best point” PSO remembers will always only non-increase in cost, but it might be very slow converging to a point where the gradient is zero ( that is -2Ax = 0)

So could you explain where your second constraint comes from and how you aim/think it should be valid (for which lambda for example)?

Feasible is again a bit vague – you will always have a point on the manifold, that is x'*x=1 by construction of the algorithms. It is not that efficient / fast in bringing your cost down – for best of cases a Euclidean or Riemannian gradient and gradient descent would be faster in that.

Best

Ronny

[BM]

Dear Ronny,

I guess, Kimmy's second condition is the first order optimality condition. @Kimmy, what is the Riemannian gradient norm that you see at the end? If it is close to zero, then the point is optimal.

Regards,

Bamdev 

[Kimmy Kong]

Dear Ronny and  Dear  BM,

thanks for your answer, 

  1) the code is exactly in your link, I did not change it at all, 

2) I understand the x*x = 1, constraint; it must hold.

3) this formula A*x./x = lambda *I (1 vector), I did not add, I just tested the result and see what it will be

because this example is to find the eigenvector. Since it is an eigenvector, it must hold A*x = lamda*x, it is the definition.

so I want to see if the result of x by PSO solver in the code can give a valid result, which means if A*x./x = lambda (1 vector),

it turns out it is not, but this means this x is not the correct solution. 

or it means the cost function is not very correct, at least it should have another constraint, 

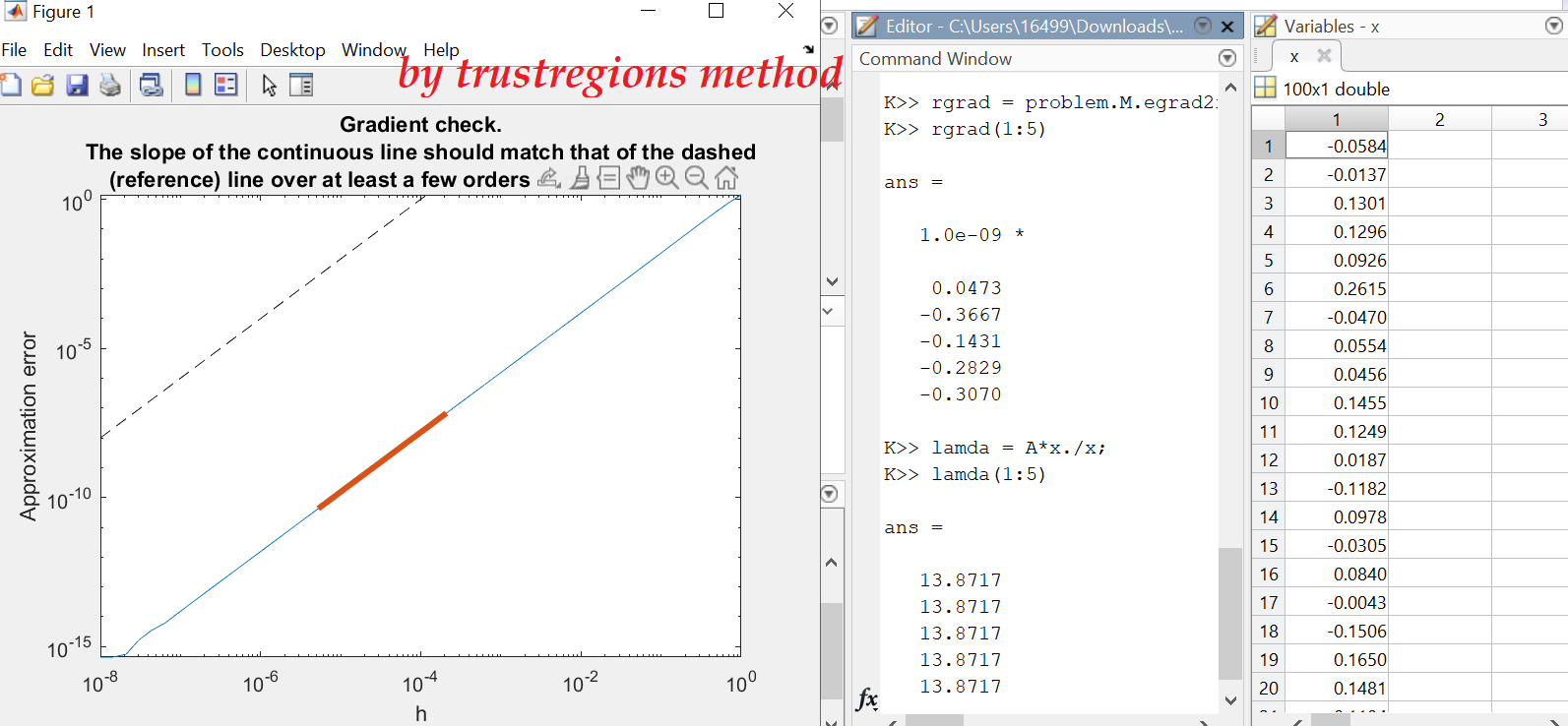
I attached two figures by PSO and trustregions, respectively, 

and for each, variable x is the output, and we know the input A, so I use it to test this equation A*x./x 

trustregions gives Reiman gradient close to 0, and lambda equal to one constant,

but PSO failed to give these results, 

That makes me to ask, PSO can not give a valid result to this problem (because the constraints is not enough just by giving xx=1),

[Ronny Bergmann]

Hi,

It is _nearly_ the optimality condition. Ax = \lambda x (lambda the largest Eigenvalue) would be ok, but you can not just divide element wise by x to get the one-vector on the left, nor is lambda known, so I doubt, that these are the right optimality conditions one would expect. It would be more like the projection of -2Ax to the tangent space should be the zero vector.

If you _know_ the lambda then you can check something, sure. And the vector of ones at least indicates that you are at _some_ eigenvector, but not more.

Besides that @Kimmy, you are a bit fast in jumping to conclusions here.

If you have the gradient and do gradient descent or trust regions – figuratively speaking – you always look from the point you are at for a very-good-way-to-continue and even find a very good step towards that direction. That is very efficient. But they need the gradient (where is it going up/downards?). So maybe imagine this like someone with a compass. Walking in a very good way towards the goal (minimiser)

Compared to that PSO is more like a bunch of fish (hence the swarm in the name), each of them “wanders around” on the manifold (here the sphere) following certain rules. they do not know the gradient (so the do not directly know which direetions are _good_ from the cost/problem), but they more like “speak to each other” and agree how to continue. So imaginge here maybe a group of kindergarten kids hopping around in the forest. They have a way of knowing who of them was the lowest (maybe their teacher keeps track), but their ways are a bit – like a swarm of fish.

A “valid result” is hence a very flexible term here. The point you end up with in PSO is surely better than where you started, but trust region is of course much more efficient. If you give PSO more time (more iterations that is) the kids will hopp around even longer / further and the result will improve.

Still: If you know the gradient – take trust_regions, not PSO. If you only have the cost – then you can not take trust_regions, so then PSO is a good way to still get “somewhere better”. But reaching a critical point might be a bit too much to ask (unless you let it run for really really long).

Best

Ronny

[Kimmy Kong]

Dear Ronny,

 thank you very much for your detailed explanations, 

I really think I got your point, PSO directs the swarms to better solutions, but it might not be a defined 'valid' solution in the middle period.

and another question always confuses me, since trustregion and conjugate methods perform very well, why do we need PSO,

 Because 

''If you only have the cost – then you can not take trust_regions,;; without gradient information, those methods may work poorly with only approximate gradient,,---- 

thank you very much for solving those.

have a nice day