Representing the "soft cube" manifold

[Michael Giglia]

Hello,

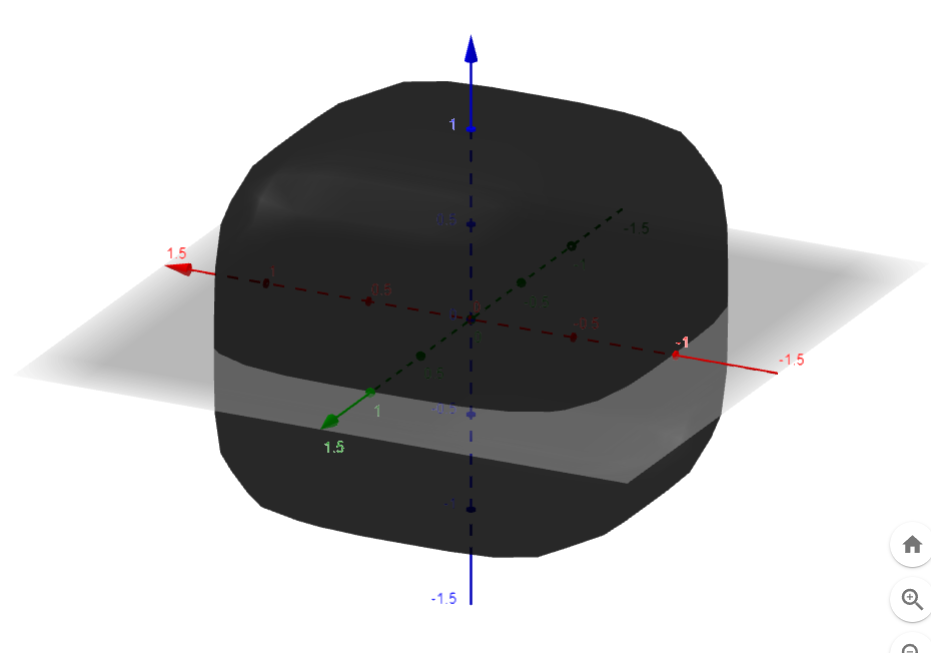
I'm curious about how (if at all possible) one could represent the surface x^4 + y^4 + z^4 = 1 as a manifold in pymanopt such that I would be able to move points along the manifold using the exponential map method that the sphere manifold has.

I'm essentially trying to model a dynamic system that can move along the surface of this "soft cube" manifold and I like how the exponential map method "wraps" the tangent vector along the manifold keeping the lengths of the tangent vector and the curve on the manifold the same (is this the property of metric invariance?). 

I'm still very new to the formal understanding of differential geometry. I understand conceptually a lot of the stuff (such as why we can locally "simplify" the manifold to the tangent space and use things like retractions or the exponential map to get back to the manifold from the ambient space) but have trouble moving from the concepts into something that can provide me numerical results.

The surface looks like this: 

Do I need to somehow "augment" the sphere so it gets warped into this shape? I imagine this wouldn't really work because the exponential map method would not be the same everywhere on this surface whereas the sphere has the same "shape" everywhere.

Hopefully this is something I can handle!

Best,

Michael Giglia

[Ronny Bergmann]

Hej,

the one thing that is similar is, to check whether a point is on your manifold (since that equation is very similar), and intuitively I would say tangent spaces should also be quite similar,

but the rest from the sphere you can not use, especially the way to “move along the surface” is probably quite different.

None of the packages I am aware of (this is the forum for Manopt, you mentioned pymanopt, I work with Manopt.jl, but there are also other packages, mainly in Python having manifolds implemented) has that manifold,

so formally you are missing how a geodesic looks like – numerically a retraction would also just work fine, if you have that (and maybe locally you want the logarithmic map – or numerically an inverse retraction as well), one could check how to realise this in one of the packages.

For the geodesic in general you have to solve an ODE for a given point p on your manifold and a tangent vector X (assuming for now the metric is the one from the embedding). With the geodesic you would have exp, sure; but as you said, that formula might be quite different. DFo you maybe have literature where they consider this manifold?

Best

Ronny

[Michael Giglia]

Hi Ronny,

How should I go about getting an ODE for the geodesic for this surface (assuming some way of using 1 equation for all points and tangent vectors)?  Where should I look for this? This seems like what I've been trying to search for online with no luck finding examples that are numerical and help me gain an intuition of how to get the exp/log map for the manifold. 

Do you know of geometric examples that explain in depth of how to determine these ODEs for manifolds that aren't "simple" like the sphere? Does it seem possible to have an analytic solution for this or will I have to resort to a different form of modelling like a neural network or something?

Thank You!

Best,

Michael Giglia

[Ronny Bergmann]

Well the first hope is you end up with something that is a formula for any p and X; for example on the sphere this has a closed form solution, see https://juliamanifolds.github.io/Manifolds.jl/stable/manifolds/sphere.html#Base.exp-Tuple{AbstractSphere,%20Vararg{Any,%20N}%20where%20N}. IN general you could read something like

Do Carmo – Riemannian Geometry, Chapter 3 on geodesics, but you need (for best of cases) a closed form solution of said ODE solution, or a first order approximation (see on the link above the available retractions for examples on the sphere.

And no please – no neural networks, you have too mich structure and knowledge available here that a neural network would be not useful, before that use some DifferentialEquations tool to solve the ODE numerically; that would not only be much more effective but also more accurate than neural networks, which are relly not useful here. I hope there is a analytic solution for the ODE.

A challenging par might then be the inverse (log or an inverse retraction). Maybe there is also already a paper of such a manifold? I just did not find much, mostly because it maybe might have a name that I do not know.

Best

Ronny 

[Michael Giglia]

Thank you Ronny I will be reading through this, hopefully I have enough capability to determine a closed form solution!

--
http://www.manopt.org
---
You received this message because you are subscribed to a topic in the Google Groups "Manopt" group.
To unsubscribe from this topic, visit https://groups.google.com/d/topic/manopttoolbox/4AiEOd1maek/unsubscribe.
To unsubscribe from this group and all its topics, send an email to manopttoolbo...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/manopttoolbox/daae3cf1-fa26-4c22-8518-0c19c3a78475n%40googlegroups.com.

[Ronny Bergmann]

Cool, looking forward to news here! If you have a solution, I can definetly help implementing that in pymanopt (and probably for comparison will implement it in Julia as well).

[Nicolas Boumal]

Hello Michael,

That's a neat setup. And I agree with everything Ronny already replied, just adding some hopefully relevant pointers.

0. If you just want the tangent spaces, that's easy: differentiate the constraint and consider its kernel. See any book on differential geometry, for example Section 3.2 in my book.

1. If all you wanted was to optimize a function over that ell_4 sphere in R^3, I would suggest you follow one of your initial instincts, namely, "somehow "augment" the sphere so it gets warped into this shape". Specifically, you'd setup a diffeomorphism phi : ell_2 Sphere -> ell_4 Sphere (that's easy to do), and compose your cost function with that diffeomorphism to bring your optimization problem to the usual sphere. Then you can roll with spherefactory in Manopt. But as you pointed out yourself, that won't preserve geodesics (the exp map).

2. If what you really want is to compute geodesics on the ell_4 sphere in R^3 (presumably with the Riemannian submanifold structure, that is, inheriting the metric from R^3), then as Ronny explained you first need to figure out the ODE that defines geodesics. It's a priori unlikely that this ODE has an explicit solution. You could plug it into Wolfram Alpha / Mathematica just in case, but most likely that will fail, and you will need to use a numerical ODE solver to compute geodesics, e.g., a Runge-Kutta type of integrator (in Matlab, that's built-in as `ode45`).

3. To figure out the ODE of geodesics, since you have just one constraint, things might not be too difficult. Basically, you need second-order differential equations for x(t), y(t) and z(t) given intitial conditions x(0), x'(0), y(0), y'(0), z(0), z'(0), where the initial velocity of course needs to be a tangent vector to your manifold at the initial point. To setup that ODE, again, you could check any Riemannian geometry textbook, and in particular you could look in my book at equation (5.44). That one tells you that for a geodesic c (which satisfies c''(t) = 0 for all t), the curve must satisfy d²c/dt² = II(dc/dt, dc/dt), where II is the second fundamental form. To get a formula for II, look at Definition 5.48 and eq. (5.33). Essentially, you need to figure out a formula for orthogonal projection to the tangent space at some point, then you need to figure out the differential of that projector with respect to the base point.

I hope this can help.

Best,

Nicolas

[Michael Giglia]

Nicolas,

Thank you very much for all of this information! I will attempt all of these methods as I believe it will be a great exercise for me since I'm relatively new to this topic.

I do believe I will need to use the second fundamental form method ultimately but I will build up to that.

I'm going to first attempt these and see if I'm capable of doing this. Then hopefully I can ask the next step of my question which would be incorporating dynamic motion onto the surface of the manifold. Imagine a car travelling along the surface of this manifold constrained by the friction of the wheels and limited steering angle, how can I find an optimal path (maybe minimum time or minimum distance) between two points on the manifold respecting these new constraints. 

But I have a ways to go before I can start messing around with that. I know I had asked a similar question before and was referenced to acadoo which is used for MPC but I'm really motivated to try and port these dynamic optimization methods using the manifold framework. Hopefully it's possible!

Thank you!

Best,

Michael Giglia 

You received this message because you are subscribed to the Google Groups "Manopt" group.
To unsubscribe from this group and stop receiving emails from it, send an email to manopttoolbo...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/manopttoolbox/2a545b5d-c138-4abc-bfe3-0947d655fb4cn%40googlegroups.com.

[Michael Giglia]

  Hello again!

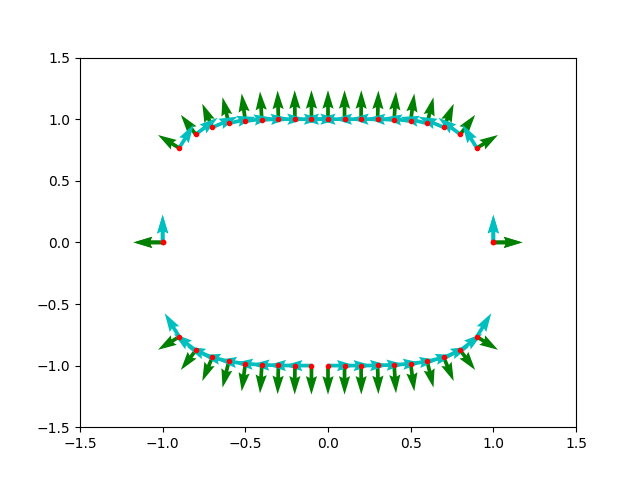
So I've finally gotten some time to try out the first method which is just finding the tangent spaces. Like I said I'm going to try going through each of these steps to really make sure I understand the fundamental math and terminology behind differential geometry and its application.

Okay so first off I simplified the problem to a 2D surface (x^4 + y^4 - 1 = 0) instead of 3D just to make my life easier for now. I also spent some time learning sympy to be able to check my hand calculations.

Okay, so differentiating this constraint (the jacobian?) gives me [4x^3, 4y^3]. Then finding the nullspace of this vector equation gives me two possibilities. 

1. [-y^3/x^3, 1] (as a column vector) 

2. [1, -x^3/y^3] (as a column vector)

I found that there must be more than one since we can have a divide by zero error because of the x or y in the denominator. I was happy to find that using sympy actually gave me one of these column vectors as the nullspace! I was really expecting to have done this incorrectly!

Finally I did some graphing to make sure that I get vectors normal to the surface and tangent to the surface (and that they are orthogonal) when using the Jacobian and the ker(Jacobian) by plugging in points along the surface. And once I fixed a bunch of plotting issues with matplotlib (mainly the quiver function does a bunch of auto scaling that makes the vectors look incorrect) the plots looked great.

So yea turned out to be quite simple once I was able to remember how to get the kernel/nullspace of a vector space. Just wanted to post to make sure I didn't do anything egregious! I'm onto attempting the method of calculating geodesics using ODEs and the second fundamental form. I imagine this will take me a while. Recently I've been watching some eigenchris on youtube and his tensor calculus examples and I see why the geodesic must satisfy c"(t)=0  as this means that the curve has no deviation from the surface. Okay some more reading and head bashing for me! Will keep this post updated! Thank you all for the help!

I apologize for my awful script. Sympy's returning types for evaluating symbolic expressions was confusing so I hacked my way through it.

[Michael Giglia]

I misspoke, I simplified the surface to be embedded in R2 (x^4 + y^4 -1 = 0) instead of embedded in R3.

[Nicolas Boumal]

Hello Michael,

Nice to read about your progress -- all looks good to me.

The plot looks fine. It could be improved by sampling the curve more uniformly. I imagine currently you sample the x-axis uniformly, then figure out the two possible values of y for each x. This creates the giant leaps on the left and right sides.

A possible alternative is to work in polar coordinates: sample theta from 0 to 2pi uniformly, then figure out the radius r > 0 such that (x, y) = (r cos theta, r sin theta) is a point on your curve (that is, such that x^4 + y^4 = 1). This should have a unique positive solution. I expect that will give you a more uniform sampling of the curve.

Also, you can probably force your plotting toolbox to give the x-axis and y-axis the same scale.

Best,

Nicolas

[Michael Giglia]

You're right I sampled along the x axis. I will move to polar coordinates, this is a great idea. Glad to see I didn't make any mistakes!

To view this discussion on the web visit https://groups.google.com/d/msgid/manopttoolbox/6278c2a4-9876-47a7-b45f-28e15d278339n%40googlegroups.com.