Is a very small gradient always possible?

[Poo Uoo]

Dear Manopt team,

 

Recently I employed the product manifold toolbox to implement a joint optimization problem of two variables.

However, I found that the cost value and norm of gradients always keep a high value (around 10^5).

So I am wondering if a small cost value and gradient can always be achieved.

Best Regards,

Xiangfeng

[Nicolas Boumal]

Hello,

Did you run checkgradient(problem) and possibly checkhessian(problem)? If so, what is the output (there should be text in the command prompt, and a plot).

Is your cost function continuously differentiable (C^1)?

Best,

Nicolas

[Poo Uoo]

Dear Nicolas

Thanks for your instructions and my code has worked.

I have a real-valued function with complex variables to minimize. 

The cost function can be expressed as f(x) = | h' * U * x |^p, where U is not a hermitian matrix, | | denotes the modulus of a complex scalar, and p >=2 is an integer.

I have derived its Euclidean gradient as

gradf(x) =  p *  | h' * U * x |^(p-2) * (h' * U * x) * U' * h.

I ran checkgradient(problem) and it passed.

But I didn't get the hessian by myself. Could you give some instructions on how to derive the hessian?

Thank you very much and Best Regards.

Xiangfeng

[Nicolas Boumal]

Dear Xiangfeng,

I need more input to help. A few things:

 * Could you copy-paste here the output of the checkgradient tool (ideally, both the text and the figure, if you can)?

 * Could you show us the code for how you create problem.M, and possibly also problem.cost and the gradient, if it's not too long.

Nicolas

[Poo Uoo]

Dear Nicolas,

Here is my considered problem and Matlab code.

Actually, I am trying to solve the problem with the product manifold framework.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clc; clear all; close all;
N = 128;
p = 20;
U = ones(N, N);
U = U - eye(N);
mu = N;
tuple.x = complexcirclefactory(N);
tuple.h = spherecomplexfactory(N, 1);
M = productmanifold(tuple);
problem.M = M;
options.maxiter = 2e4;
options.tolgradnorm = 1e-6; % tolerance on gradient norm
options.minstepsize = 1e-10;
problem.cost = @(X) func_my_cost(X, U, p, mu);
problem.egrad = @(X) func_my_grad(X, U, p, mu);
checkgradient(problem);
[X, cost, info, options] = conjugategradient(problem,[],options);
x = X.x; h = X.h;
h = sqrt(N) * h;
MF1 = conv(flip(conj(h)), x);
figure;plot(db(MF1/sqrt(N*N)));
%%
function cost = func_my_cost(X, U, p, mu)
x = X.x;
h = X.h;
cost = abs(h'*U*x)^p + abs(h'*x - mu)^p;
end
function grad = func_my_grad(X, U, p, mu)
x = X.x;
h = X.h;
grad.x = p*abs(h'*U*x)^(p-2) * (h' * U * x) * U' * h + p * (abs(h' * x - mu)^(p-2)) * (h'*x - mu) * h;
grad.h = p*abs(h'*U*x)^(p-2) * (h' * U * x)' * U * x + p * (abs(h' * x - mu)^(p-2)) * (x'*h - mu) * x;
end

[Nicolas Boumal]

Hello,

When I run this code, I get the following output (emphasis in bold is mine):

The slope should be 2. It appears to be: 2.00041.
If it is far from 2, then directional derivatives might be erroneous.
The residual should be 0, or very close. Residual: 2.65562e+25.
If it is far from 0, then the gradient is not in the tangent space.

The slope is fine, but the residual seems entirely off (it's huge). This would suggest that the gradient is not properly projected, but actually not.
Indeed, if we pick a random point on the manifold and compute the norm of the gradient there, we get an even bigger number:

>> x = problem.M.rand();

>> problem.M.norm(x, getGradient(problem, x))
ans =
   2.4849e+42

The ratio between 10^25 and 10^42 is indeed machine precision, so your gradient appears to be correct.

And indeed, when we run nonlinear conjugate gradients, we get this output (from your code):

 iter                cost val     grad. norm
    0 +1.5189654937419912e+42 2.67572166e+42
    1 +6.7334922053171432e+41 1.13133108e+42
    2 +4.8204183533551820e+41 7.30252036e+41
    3 +3.3511451234617862e+41 4.00287658e+41
    4 +2.5272662321494862e+41 1.84276234e+41
    5 +2.2195981445610432e+41 5.08341667e+40
    6 +2.1935520964569974e+41 1.79949772e+40
    7 +2.1902579606196875e+41 6.50844406e+39
    8 +2.1898265305729956e+41 2.36058383e+39
    9 +2.1897697667012173e+41 8.56556861e+38
   10 +2.1897622924954353e+41 3.10852006e+38
   11 +2.1897613080947600e+41 1.12822097e+38
   12 +2.1897611784175141e+41 4.09520128e+37
   13 +2.1897611613316668e+41 1.48660811e+37
   14 +2.1897611590800744e+41 5.39706600e+36
   15 +2.1897611587833031e+41 1.95956102e+36
   16 +2.1897611587441753e+41 7.11540341e+35
   17 +2.1897611587390177e+41 2.58392415e+35
   18 +2.1897611587383399e+41 9.38424432e+34
   19 +2.1897611587382494e+41 3.40845814e+34
   20 +2.1897611587382386e+41 1.23809944e+34
   21 +2.1897611587382335e+41 4.49771327e+33
   22 +2.1897611587382335e+41 1.63405416e+33
   23 +2.1897611587382335e+41 5.93716784e+32
   24 +2.1897611587382335e+41 1.62271681e+32
   25 +2.1897611587382335e+41 1.62306806e+32

This shows that the method behaves well: the gradient norm is reduced by 10 orders of magnitude, and the cost function value decreases by about one order of magnitude. It's just that the scaling of the cost function is humongous.

It is probably a good idea to rescale your cost function to bring those numbers back to more typical ranges, because they might cause some numerical issues. Apart from that, all looks normal to me.

Best,

Nicolas

[Poo Uoo]

Dear Nicolas,

Thanks for your valuable explanations.

Further, if I want to employ the Riemannian trust region algorithm to solve this problem, how to derive the Riemannian Hessian or directional derivations?

I think it is truly hard since it is a high-order optimization.

Thank you very much and best regards.

Xiangfeng

[Nicolas Boumal]

Hello,

You can run trustregions(problem) even if you do not specify the Hessian. In that case, Manopt will approximate the Hessian automatically with finite differences, which usually works quite well. (The scaling issues discussed above might create difficulties here, though).

Otherwise, to get the Euclidean Hessian, you just need to differentiate the Euclidean gradient (directional derivative). Put that in problem.ehess, and Manopt will convert it to the Riemannian Hessian automatically. Don't forget to run checkhessian(problem).

Best,

Nicolas

--
http://www.manopt.org
---
You received this message because you are subscribed to a topic in the Google Groups "Manopt" group.
To unsubscribe from this topic, visit https://groups.google.com/d/topic/manopttoolbox/3Cnf5uWdL28/unsubscribe.
To unsubscribe from this group and all its topics, send an email to manopttoolbo...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/manopttoolbox/cb38c00e-2e6e-4dd3-b632-fd45e91f2129n%40googlegroups.com.

[Poo Uoo]

Dear Nicolas,

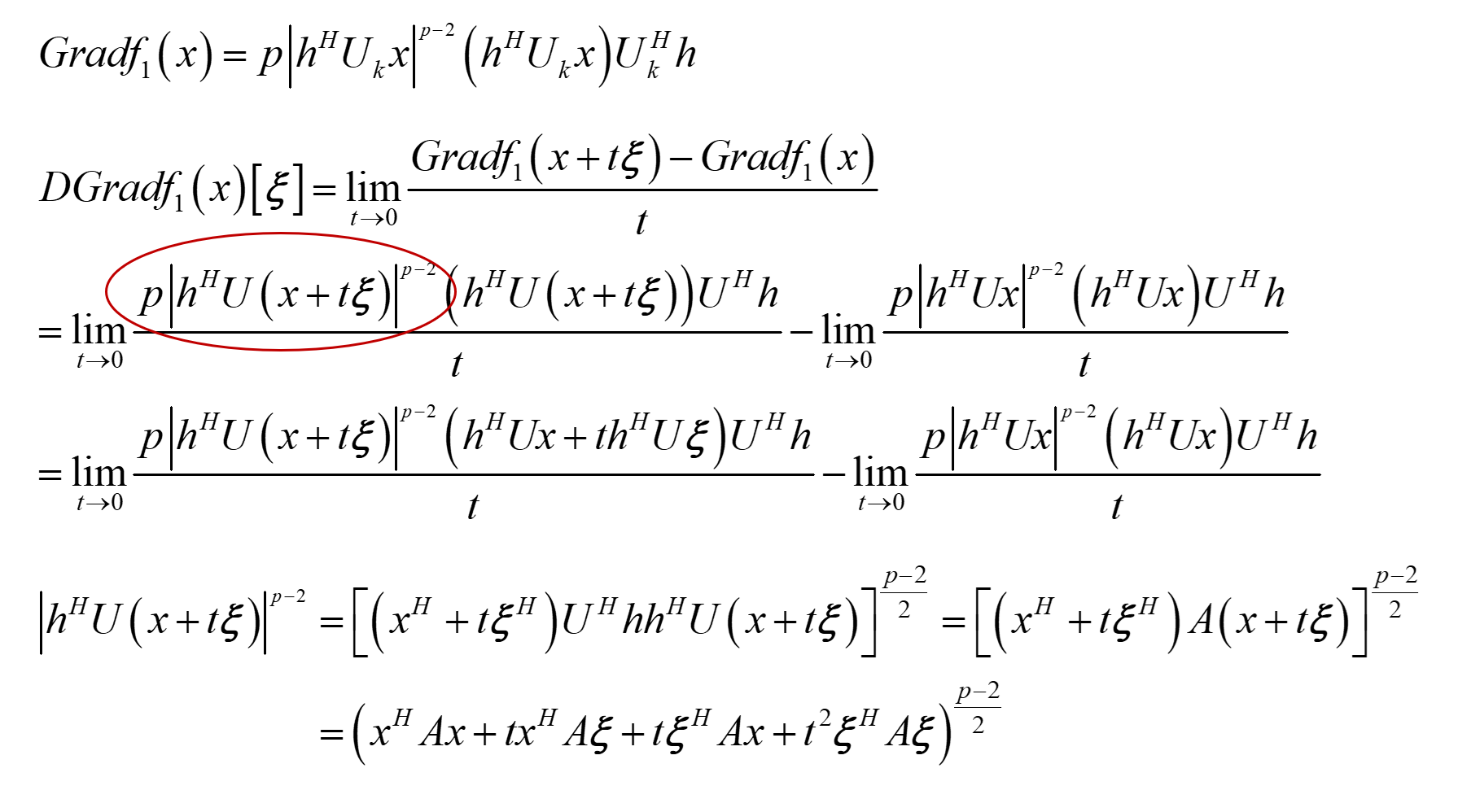
Thanks for your kind instruction.

I am trying to derive the Euclidean Hessian of the cost function but running into some difficulties.

The main problem is the inability to expand higher-order summation terms (as shown in the figure). 

I tried to solve it using the generalized binomial theorem, but it produced too many terms. 

Do you have any other solution?

Thanks very much and best regards.

Xiangfeng

[Nicolas Boumal]

I imagine the difficulties stem from the term |x|^{p-1}. Perhaps if you rewrite it as (|x|²)^{(p-2)/2} things become easier? Then, you just need to see this as a composition of the function that raises a real number to the power (p-2)/2 (which has an easy derivative) together with the function that maps a complex number to the square of its module (which also has an easy derivative). Chain rule for the composition.

Best,

Nicolas

[Poo Uoo]

Dear Nicolas,

Sorry, I didn't understand your idea well. 

Since I want to calculate the directional derivative from the definition, it is necessary to expand the higher-order terms and then try to remove the terms containing t.

The chain rule does not seem to apply to this process. Could you please explain this in more detail?

Best,

Xiangfeng

[Nicolas Boumal]

As an example, let f(x) = ||x||^3.

The norm of a vector is ||x|| = sqrt(<x, x>) where <u, v> is your inner product. So, we can equivalently write: f(x) = (<x, x>)^(3/2).

This is a composition of the function g(x) = <x, x> together with the real function h(t) = t^(3/2).  Explicitly: f(x) = h(g(x)).

Since it is a composition, we can differentiate using the chain rule: f = h o g and therefore Df(x)[u] = Dh(g(x))[Dg(x)[u]].

Since h is just a scalar function, its differential is just its usual derivative. So, Df(x)[u] = h'(g(x))  Dg(x)[u].

It remains to check that h'(t) = (3/2) t^(1/2)  and that Dg(x)[u] = 2<x, u>, and to put it together for Df.