Solomonoff induction using probabilistic programs
39 views
Skip to first unread message
Nil Geisweiller
Jun 5, 2016, 1:18:30 AM6/5/16
to MAGIC
Hi,
do you know any paper on Solomonoff induction where the posterior is
not built using only deterministic programs but also probabilistic
ones.
By probabilistic programs I mean either
1. indeterministic programs that if run a large number of times will
give an estimate of the probability of P(xt|x1:t-1) (conditional
probability of observing the next bit given the bitstring history).
2. or programs that given x1:t-1 will directly calculate P(xt|x1:t-1).
In such cases, the probability of a certain program p being a model of
a certain bitstring history, P(p|x1:t-1) will not be 0 or 1, instead
it will usually be < 1. So the overall impact of such program on the
estimate of the posterior will be less than a perfectly fit
deterministic program. However one may suspect that most of these
partially unfit programs will be shorter as well, so in the end they
might really have a big impact. Anyway, I suppose that wouldn't change
anything regarding the convergence theorem, which should still holds
in the same manner.
Anybody knows anything about that?
Thanks,
Nil
do you know any paper on Solomonoff induction where the posterior is
not built using only deterministic programs but also probabilistic
ones.
By probabilistic programs I mean either
1. indeterministic programs that if run a large number of times will
give an estimate of the probability of P(xt|x1:t-1) (conditional
probability of observing the next bit given the bitstring history).
2. or programs that given x1:t-1 will directly calculate P(xt|x1:t-1).
In such cases, the probability of a certain program p being a model of
a certain bitstring history, P(p|x1:t-1) will not be 0 or 1, instead
it will usually be < 1. So the overall impact of such program on the
estimate of the posterior will be less than a perfectly fit
deterministic program. However one may suspect that most of these
partially unfit programs will be shorter as well, so in the end they
might really have a big impact. Anyway, I suppose that wouldn't change
anything regarding the convergence theorem, which should still holds
in the same manner.
Anybody knows anything about that?
Thanks,
Nil
Laurent
Jun 5, 2016, 5:54:34 AM6/5/16
to magic...@googlegroups.com
Hi Nil,
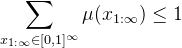
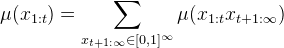

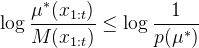
Yes, the first to show the equivalence between Solomonoff's set of the deterministic models and a set of stochastic model (semi-computable semi-measures) is Levin. See http://www.scholarpedia.org/article/Algorithmic_probability
and See Chapters 4 and 5 of the Li&Vitányi book.
This formulation has been used by many others, in particular in Hutter's book on Universal AI. See also the more readable thesis by Legg: www.vetta.org/documents/Machine_Super_Intelligence.pdf
The usual formulation relies on measure theory, but it's perfectly fine to use your probabilistic formulation (in particular your second point). A bit more precisely but with some simplifications, a semi-measure µ assigns a probability weight µ(x_{1:oo}) to all infinite strings x_{1:oo}, and they must sum to 1 (or at most 1, hence "semi-"measure):
Note that some (many) strings may have a zero weight. (In particular, in the case of a deterministic µ, only a single infinite sequence has a unitary weight, all others have a zero weight.)
Then, the probability of a finite prefix string x_{1:t} is just the sum of the weights this measures assigns to all strings that start with this prefix:
The conditional probability follows by definition:
From a more practical point of view, you can also start with the conditional probability, ensuring it sums to at most 1, and work your way backwards as in your point 2.
Now define the Solomonoff-Levin mixture M, where p(µ) is the prior weight of µ, and is positive for any (semi-)computable µ (and they must sum to at most 1):
M(x_{1:t}) = \sum_µ p(µ) µ(x_{1:t})
Then we easily obtain that, for any µ and in particular the "source" µ* that generates the sequence x_{1:t}:
M(x_{1:t}) ≥ p(µ*) µ*(x_{1:t})
(assuming the source is (semi-)computable)
i.e., M dominates µ*. Since p(µ*) is a constant independent of x_{1:t}, M is almost as good as the source. We often use the logarithmic loss to compare two probabilistic models:
-log(M(x_{1:t}) ≤ -log(µ*(x_{1:t})) -log P(µ*)
or as a "redundancy" of M to µ*:
In particular if p(µ*)= 2^{-K(µ*)} then the redundancy of M compared to µ* is at most K(µ*). Looks pretty hard to beat that :)
Levin showed that the probabilistic formulation is equivalent (up to some constant dependent on the reference machine) to the Solomonoff's formulation with deterministic programs. Hutter showed that there exists a reference machine for which this constant is 0 (IIRC).
Hope this helps,
Laurent
--
Before posting, please read this: https://groups.google.com/forum/#!topic/magic-list/_nC7PGmCAE4
---
You received this message because you are subscribed to the Google Groups "MAGIC" group.
To unsubscribe from this group and stop receiving emails from it, send an email to magic-list+...@googlegroups.com.
To post to this group, send email to magic...@googlegroups.com.
Visit this group at https://groups.google.com/group/magic-list.
Nil Geisweiller
Jun 14, 2016, 6:03:56 AM6/14/16
to magic...@googlegroups.com
Yes it helps Laurent! I had read some of this 10 years ago but I didn't
connect all the dots at the time (I didn't really need to back then).
Time is ripe. Thanks!
Nil
On 06/05/2016 12:54 PM, Laurent wrote:
> Hi Nil,
>
> Yes, the first to show the equivalence between Solomonoff's set of the
> deterministic models and a set of stochastic model (semi-computable
> semi-measures) is Levin. See
> http://www.scholarpedia.org/article/Algorithmic_probability
> and See Chapters 4 and 5 of the Li&Vitányi book.
>
> This formulation has been used by many others, in particular in Hutter's
> book on Universal AI. See also the more readable thesis by Legg:
> www.vetta.org/documents/Machine_Super_Intelligence.pdf
> <http://www.vetta.org/documents/Machine_Super_Intelligence.pdf>
> <mailto:magic-list+...@googlegroups.com>.
connect all the dots at the time (I didn't really need to back then).
Time is ripe. Thanks!
Nil
On 06/05/2016 12:54 PM, Laurent wrote:
> Hi Nil,
>
> Yes, the first to show the equivalence between Solomonoff's set of the
> deterministic models and a set of stochastic model (semi-computable
> semi-measures) is Levin. See
> http://www.scholarpedia.org/article/Algorithmic_probability
> and See Chapters 4 and 5 of the Li&Vitányi book.
>
> This formulation has been used by many others, in particular in Hutter's
> book on Universal AI. See also the more readable thesis by Legg:
> www.vetta.org/documents/Machine_Super_Intelligence.pdf
>
> The usual formulation relies on measure theory, but it's perfectly fine
> to use your probabilistic formulation (in particular your second point).
> A bit more precisely but with some simplifications, a semi-measure µ
> assigns a probability weight µ(x_{1:oo}) to all infinite strings
> x_{1:oo}, and they must sum to 1 (or at most 1, hence "semi-"measure):
> The usual formulation relies on measure theory, but it's perfectly fine
> to use your probabilistic formulation (in particular your second point).
> A bit more precisely but with some simplifications, a semi-measure µ
> assigns a probability weight µ(x_{1:oo}) to all infinite strings
> x_{1:oo}, and they must sum to 1 (or at most 1, hence "semi-"measure):
> Inline image 1
>
> Note that some (many) strings may have a zero weight. (In particular, in
> the case of a deterministic µ, only a single infinite sequence has a
> unitary weight, all others have a zero weight.)
>
> Then, the probability of a finite prefix string x_{1:t} is just the sum
> of the weights this measures assigns to all strings that start with this
> prefix:
>
> Note that some (many) strings may have a zero weight. (In particular, in
> the case of a deterministic µ, only a single infinite sequence has a
> unitary weight, all others have a zero weight.)
>
> Then, the probability of a finite prefix string x_{1:t} is just the sum
> of the weights this measures assigns to all strings that start with this
> prefix:
> Inline image 2
>
> The conditional probability follows by definition:
>
> The conditional probability follows by definition:
> Inline image 3
>
> From a more practical point of view, you can also start with the
> conditional probability, ensuring it sums to at most 1, and work your
> way backwards as in your point 2.
>
> Now define the Solomonoff-Levin mixture M, where p(µ) is the prior
> weight of µ, and is positive for any (semi-)computable µ (and they must
> sum to at most 1):
> M(x_{1:t}) = \sum_µ p(µ) µ(x_{1:t})
>
> Then we easily obtain that, for any µ and in particular the "source" µ*
> that generates the sequence x_{1:t}:
> M(x_{1:t}) ≥ p(µ*) µ*(x_{1:t})
>
> (assuming the source is (semi-)computable)
>
> i.e., M dominates µ*. Since p(µ*) is a constant independent of x_{1:t},
> M is almost as good as the source. We often use the logarithmic loss to
> compare two probabilistic models:
> -log(M(x_{1:t}) ≤ -log(µ*(x_{1:t})) -log P(µ*)
>
> or as a "redundancy" of M to µ*:
>
> From a more practical point of view, you can also start with the
> conditional probability, ensuring it sums to at most 1, and work your
> way backwards as in your point 2.
>
> Now define the Solomonoff-Levin mixture M, where p(µ) is the prior
> weight of µ, and is positive for any (semi-)computable µ (and they must
> sum to at most 1):
> M(x_{1:t}) = \sum_µ p(µ) µ(x_{1:t})
>
> Then we easily obtain that, for any µ and in particular the "source" µ*
> that generates the sequence x_{1:t}:
> M(x_{1:t}) ≥ p(µ*) µ*(x_{1:t})
>
> (assuming the source is (semi-)computable)
>
> i.e., M dominates µ*. Since p(µ*) is a constant independent of x_{1:t},
> M is almost as good as the source. We often use the logarithmic loss to
> compare two probabilistic models:
> -log(M(x_{1:t}) ≤ -log(µ*(x_{1:t})) -log P(µ*)
>
> or as a "redundancy" of M to µ*:
> To post to this group, send email to magic...@googlegroups.com
> <mailto:magic...@googlegroups.com>.
> --
> Before posting, please read this:
> https://groups.google.com/forum/#!topic/magic-list/_nC7PGmCAE4
> ---
> You received this message because you are subscribed to the Google
> Groups "MAGIC" group.
> To unsubscribe from this group and stop receiving emails from it, send
> an email to magic-list+...@googlegroups.com
> <mailto:magic-list+...@googlegroups.com>.
> Before posting, please read this:
> https://groups.google.com/forum/#!topic/magic-list/_nC7PGmCAE4
> ---
> You received this message because you are subscribed to the Google
> Groups "MAGIC" group.
> To unsubscribe from this group and stop receiving emails from it, send
> an email to magic-list+...@googlegroups.com
> To post to this group, send email to magic...@googlegroups.com
> <mailto:magic...@googlegroups.com>.
Reply all
Reply to author
Forward
0 new messages
