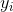minimize with covariance matrix
ANA ISABEL
Matt Newville
ANA ISABEL
Matt Newville
Hi,
When I minimize I do:result = minimize(residual, pars, args=(y, x, None, cov))What does exactly minimize do?
Sorry that's either to vague or too big a topic. You've read the documentation, right? Was something there unclear?
If it's just minimizing residual function then the answer is easy because I just have to minimize the chi2:
def residual(pars, data, x, error, icov):a = pars['a'].valueb = pars['b'].valuec = pars['c'].valueamp = pars['amp'].valuethb = pars['thb'].valuesigma = pars['sigma'].valuebackground=a+b*pow(x,-c)BAO=amp*np.exp(-(x-thb)*(x-thb)/(2*sigma*sigma))model=background+BAOresid = modelif data is not None:resid = np.dot(model - data,model-data)if error is not None:resid = resid / error**2if cov is not None:resid = np.dot(model - data,np.dot(icov,model-data))return residWhat I do not have clear is if then the chi**2 calculated by minimize would be fine, but I can calculate it myself anyway.
How do you calculate the error of the parameters?
ANA ISABEL
Matt Newville
Hi,I have a covariance matrix because the points in my function are correlated, I can calculate this theoretically or with simulations or doing jack-knife.
ANA ISABEL
On Sunday, April 10, 2016 at 9:00:34 PM UTC+1, ANA ISABEL wrote:
Stefano Renzo Garcia Castañeda
- sigma : None or M-length sequence or MxM array, optional
Determines the uncertainty in ydata. If we define residuals as
r = ydata - f(xdata, *popt), then the interpretation of sigma depends on its number of dimensions:
A 1-d sigma should contain values of standard deviations of errors in ydata. In this case, the optimized function is
chisq = sum((r / sigma) ** 2).A 2-d sigma should contain the covariance matrix of errors in ydata. In this case, the optimized function is
chisq = r.T @ inv(sigma) @ r.New in version 0.19.
None (default) is equivalent of 1-d sigma filled with ones.
Matt Newville
Hi Matt,I just found lmfit and I am very tempted to use it. However, I have the same need as Ana. My data has errors which are correlated. That is, the errors of my data are not independent. For instance, if the error of the parameter[1] happens to increase, the error of the parameter[3] will do as well (in a very particular way). And similar for the rest of the parameters.
This happens when the data to be fitted is not independent but it is correlated. This should affect the fit process somehow.
The way in which the data is correlated is captured in the correlation matrix of the data (different from the correlation matrix obtained as result of fitting model, which will depend on the particular fitted model).The function curve_fit from SciPy allow us to account for this by mean of the sigma parameter:
- sigma : None or M-length sequence or MxM array, optional
Determines the uncertainty in ydata. If we define residuals as
r = ydata - f(xdata, *popt), then the interpretation of sigma depends on its number of dimensions:
A 1-d sigma should contain values of standard deviations of errors in ydata. In this case, the optimized function is
chisq = sum((r / sigma) ** 2).A 2-d sigma should contain the covariance matrix of errors in ydata. In this case, the optimized function is
chisq = r.T @ inv(sigma) @ r.New in version 0.19.
None (default) is equivalent of 1-d sigma filled with ones.
That is, instead of giving a simple 1D array containing the uncertainty of each data value, we can give a 2D array (the covariance matrix of the data. Not the covariance matrix of the fit) to perform the fit.My question: Is something equivalent possible in mlfit?
Stefano Renzo Garcia Castañeda
I just found lmfit and I am very tempted to use it. However, I have the same need as Ana. My data has errors which are correlated. That is, the errors of my data are not independent. For instance, if the error of the
parameterdata[1] happens to increase, the error of theparameterdata[3] will do as well (in a very particular way). And similar for the rest of theparametersdata.
In a fit process, what is often minimized is the Chi squared χ2 :Where:
- is the data (measurements)
- are the model function and its parameters
- is the uncertainty in the data
- is the residual
Usually, each measurement of our data set is independent and has no correlation with any other element from the dataset. Thenis simply a 1D array where each
tells about each
. In fact,
is just the diagonal of the covariance matrix of our dataset. And the covariance matrix happens to be a pure diagonal matrix with all the off-diagonals equal to 0.
If each measurement of our data set is not independent, then the covariance matrix of our data set is not a diagonal matrix and this can be accounted for by minimizing a so-called "generalized Chi squared"This is the χ2 that I would like to obtain from lmfit.
My concrete problem is that I have observed databut what I need to fit is the transformation
which will lead to a non-diagonal covariance matrix for the new dataset
. In particular, the covariance matrix of
will be non zero in the diagonal and in the first off-diagonals.
Stefano Renzo Garcia Castañeda
Thank you for your prompt answer. You are right, I expressed myself confusing. Please find below the corrected version of the paragraph that you quoted:
I just found lmfit and I am very tempted to use it. However, I have the same need as Ana. My data has errors which are correlated. That is, the errors of my data are not independent. For instance, if the error of the
parameterdata[1] happens to increase, the error of theparameterdata[3] will do as well (in a very particular way). And similar for the rest of theparametersdata.
In a fit process, what is often minimized is the Chi squared χ2 :
Where:Usually, each measurement of our data set is independent and has no correlation with any other element from the dataset. Then
is simply a 1D array where each
tells about each
. In fact,
is just the diagonal of the covariance matrix of our dataset. And the covariance matrix happens to be a pure diagonal matrix with all the off-diagonals equal to 0.
If each measurement of our data set is not independent, then the covariance matrix of our data set is not a diagonal matrix and this can be accounted for by minimizing a so-called "generalized Chi squared"
This is the χ2 that I would like to obtain from lmfit.
By now, I will check what `cholesky` and `solve_triangular` are. If that does not suffice, I will try to make a pull request.
For your information:
Best,
Stefano
On Thursday, May 31, 2018 at 4:30:44 AM UTC+2, Matt Newville wrote: