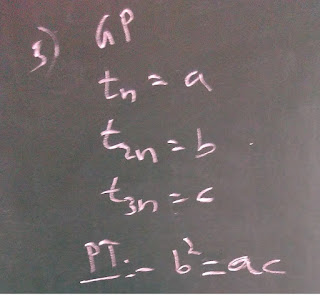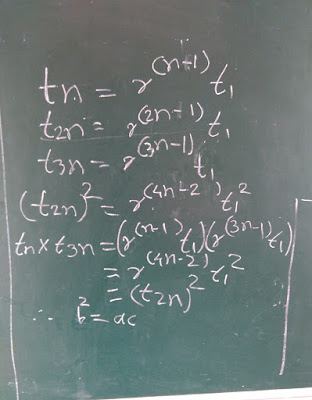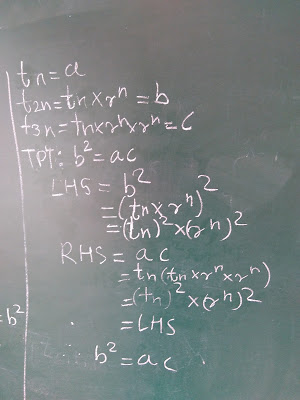When students are not directly fed the text-book methods - A.P. - Part-2

1 view

Skip to first unread message

Rupesh Gesota

unread,

Jun 11, 2018, 10:21:14 PM6/11/18

to Rupesh Gesota

Hello folks,

So as I had said, I am back again with the Part-2 of this story :-)

Hope you remember about the onset of an unusual activity in our class? - my (lower grade) students have started doing (& enjoying) Maths from (higher-grade) text-books. Its an unusual activity not just because of the different in the class-levels, but because we had never used any text-books till now! :-))

In the previous post, I had shared about their exploration of problems based on AP (arithmetic progression) and I am happy that many of you liked their different approaches to solve one of the problems. For those, who haven't read the previous post yet, this is the link:

http://rupeshgesota.blogspot.com/2018/06/when-students-are-not-directly-fed-text.html

So after solving some more AP-based problems (should we really call them problems? :-), we moved on to GP (Geometric progression).

In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3.

As we did in AP, here too I asked them to figure out the formula for -

a) nth term of GP and then,

b) sum of first n terms of GP

They found the former quickly but needed some help in the second case.

Then I gave them around 4-5 problems at a stretch, out of which first few were quite easy.

This one took some time, but I am glad they could solve it.

I would again suggest you to (try to) solve this on your own first....

....

Following are the solutions of students:

Method-1: by Vaishnavi

Method-2: by Jitu

Method-3 - by Rohit

Yes, Rohit's method is somewhat similar to that of Vaishnavi's. But the reason I have shared it because he has worked out on his own and secondly, his representation is little different than that of Vaishnavi.

1) How did you solve this problem?

2) Your views about their approaches?

PS: These students are from grade-7 and 8 Marathi medium government school and are part of a maths enrichment program- MENTOR. To know more, check www.supportmentor.weebly.com

Thanks and Regards

Rupesh Gesota Maths Educator, Program MENTOR
Mobile: +91 9594 02 03 04 Email: rupesh...@gmail.com Website: www.supportmentor.weebly.com Blog: www.rupeshgesota.blogspot.com