New semTools function for testing measurement equivalence / invariance
Terrence Jorgensen
- measurementInvariance(): only for numeric indicators, only tests across multiple groups
- measurementInvarianceCat(): only for ordered indicators, only tests across multiple groups
- longInvariance(): only for numeric indicators of 1 (repeatedly measured) factor, only tests across repeated measures
devtools::install_github("simsem/semTools/semTools")
library(semTools)
?measEq.syntaxGiacomo Mason
Giacomo Mason
On Sunday, August 26, 2018 at 11:02:43 PM UTC+1, Terrence Jorgensen wrote:
Terrence Jorgensen
I can't seem to be able to install semTools from GitHub using devtools
library(devtools)Carlos Lemos
--
You received this message because you are subscribed to the Google Groups "lavaan" group.
To unsubscribe from this group and stop receiving emails from it, send an email to lavaan+un...@googlegroups.com.
To post to this group, send email to lav...@googlegroups.com.
Visit this group at https://groups.google.com/group/lavaan.
For more options, visit https://groups.google.com/d/optout.
Carlos Lemos
I’m trying to use the new measEq.Syntax() function to study measurement invariance on the ISSP religion data. Here is the structure of the data frame:
> str(df)
'data.frame': 35198 obs. of 20 variables:
$ V28 : Ord.factor w/ 3 levels "I don't believe in God"<..: 3 3 2 2 2 2 2 2 2 2 ...
$ V30 : Ord.factor w/ 4 levels "No, definitely not"<..: 2 4 2 2 4 NA 1 NA 2 1 ...
$ V31 : Ord.factor w/ 4 levels "No, definitely not"<..: 2 4 2 1 NA 1 1 NA 1 3 ...
$ V32 : Ord.factor w/ 4 levels "No, definitely not"<..: 2 2 2 1 NA 1 1 1 2 3 ...
$ V33 : Ord.factor w/ 4 levels "No, definitely not"<..: 3 4 2 1 1 3 1 2 2 3 ...
$ V35 : Ord.factor w/ 5 levels "Strongly disagree"<..: 2 5 3 1 2 NA 1 3 3 NA ...
$ V37 : Ord.factor w/ 5 levels "Strongly disagree"<..: 3 2 3 1 1 1 1 3 3 NA ...
$ V46 : Ord.factor w/ 4 levels "Never"<"Yearly"<..: 4 3 3 1 2 2 3 2 1 3 ...
$ V47 : Ord.factor w/ 4 levels "Never"<"Yearly"<..: 3 NA 2 1 2 NA 1 1 1 3 ...
$ V48 : Ord.factor w/ 4 levels "Never"<"Yearly"<..: 4 4 2 1 2 4 3 1 2 3 ...
$ V49 : Ord.factor w/ 5 levels "Never"<"Yearly"<..: 4 1 2 1 1 1 1 1 1 3 ...
$ V50 : Ord.factor w/ 5 levels "Never"<"Yearly"<..: 2 1 1 2 1 1 1 1 1 2 ...
$ V51 : Ord.factor w/ 5 levels "Highly non-religious"<..: 4 1 2 1 1 4 2 2 2 2 ...
$ ATTEND : Ord.factor w/ 4 levels "Never"<"Yearly"<..: 4 1 2 1 1 2 1 1 1 3 ...
$ AGE : Ord.factor w/ 5 levels "0-24"<"25-44"<..: 4 2 2 2 2 3 3 3 3 3 ...
$ SEX : Factor w/ 2 levels "Male","Female": 2 2 1 1 1 1 2 1 1 2 ...
$ DEGREE : Ord.factor w/ 6 levels "No formal qualification"<..: 2 4 4 6 4 6 3 3 4 3 ...
$ RELIGGRP : Factor w/ 5 levels "No religion",..: 2 2 4 1 1 1 2 1 1 2 ...
$ COUNTRY.NAME: Factor w/ 26 levels "AU-Australia",..: 2 3 4 5 7 8 9 12 13 17 ...
$ YEAR : Ord.factor w/ 1 level "2008": 1 1 1 1 1 1 1 1 1 1 ...
>
>
I defined the following items as ordinal and converted to numeric, and for simplicity I used “SEX” as the group factor (just two levels):
> indicators <- c("V28", "V30", "V31", "V32", "V33",
+ "V35", "V37",
+ "V46", "V47", "V48", "V49", "V50",
+ "V51", "ATTEND")
> for (ind in indicators) {
+ df[,ind] <- as.numeric(df[,ind])
+ }
> group <- "SEX"
>
I now tried to compute a configural model, first with “cfa” and then with “measEq.syntax”, for a single factor:
> model <- "afterlife =~ V30 + V31 + V32 + V33"
> # CONFIGURAL
> config <- cfa(model, data = df, ordered = indicators, parameterization = "theta",
+ estimator = "WLSMV", group = group, group.equal = "")
> config <- measEq.syntax(model, data = df, ordered = indicators, parameterization = "theta",
+ ID.fac = "std.lv", ID.cat = "Wu.Estabrook.2016", estimator = "WLSMV",
+ group = group, group.equal = "", return.fit = TRUE)
Error in specify[[1]][RR, CC] : subscript out of bounds
>
The first runs, the second gives an error. However, if I define this 2-factor model:
model <- "afterlife =~ V30 + V31 + V32 + V33
belief.God =~ V28 + V35 + V37"
it runs OK:
> config <- cfa(model, data = df, ordered = indicators, parameterization = "theta",
+ estimator = "WLSMV", group = group, group.equal = "")
> config <- measEq.syntax(model, data = df, ordered = indicators, parameterization = "theta",
+ ID.fac = "std.lv", ID.cat = "Wu.Estabrook.2016", estimator = "WLSMV",
+ group = group, group.equal = "", return.fit = TRUE)
>
What am I doing wrong?
I proceeded to compute a model with constrained thresholds and loadings, which tests for metric invariance (scales of both latent response variables and factors fixed across groups):
> metric <- measEq.syntax(model, data = df, ordered = indicators, parameterization = "theta",
+ ID.fac = "std.lv", ID.cat = "Wu.Estabrook.2016", estimator = "WLSMV",
+ group = group, group.equal = c("thresholds","loadings"),
return.fit = TRUE)
>
and it runs OK and has good fit (cfi = 0.99936, rmsea = 0.03707745, srmr = 0.0183). I inspected the parameter table and checked that the identification conditions in eq. (19) of Wu and Estabrook are nicely in place (thank you very much for this!!!). However, when I check the estimator:
> unlist(lavInspect(metric, what = "Options"))["estimator"]
estimator
"DWLS"
>
I don’t get “WLSMV”, which is recommended for MGCFA with ordinal variables.
Finally, I have another doubt. I’m trying to run multiple imputed files with measEq.syntax(), but since this takes a long time with “mice”, I thought of saving the imputed data frames in a “mids” object and then running the analysis. However, I could not figure out how to do this with the help page of measEq.syntax().
Thank you very much once again for writing this wonderful function and for your help and attention.
Sincerely,
Carlos M. Lemos
dvillarre...@gmail.com
Hi Terrence,
Thank you very much for this function.
I have a problem running my model, it is a longitudinal invariance analysis with categorical variables.
They are a total of seven measurements (DEP0 to DEP6), with nine items in each measurement. The items score from 0 to 3, however, in some follow-ups the items only reach scores from 0 to 2.
model <- "
DEP0 =~ f0V1 + f0V2 + f0V3 + f0V4 + f0V5 + f0V6 + f0V7 + f0V8 + f0V9
DEP1 =~ f1V1 + f1V2 + f1V3 + f1V4 + f1V5 + f1V6 + f1V7 + f1V8 + f1V9
DEP2 =~ f2V1 + f2V2 + f2V3 + f2V4 + f2V5 + f2V6 + f2V7 + f2V8 + f2V9
DEP3 =~ f3V1 + f3V2 + f3V3 + f3V4 + f3V5 + f3V6 + f3V7 + f3V8 + f3V9
DEP4 =~ f4V1 + f4V2 + f4V3 + f4V4 + f4V5 + f4V6 + f4V7 + f4V8 + f4V9
DEP5 =~ f5V1 + f5V2 + f5V3 + f5V4 + f5V5 + f5V6 + f5V7 + f5V8 + f5V9
DEP6 =~ f6V1 + f6V2 + f6V3 + f6V4 + f6V5 + f6V6 + f6V7 + f6V8 + f6V9
"
var0 <- c("f0V1", "f0V2", "f0V3", "f0V4", "f0V5", "f0V6", "f0V7", "f0V8", "f0V9")
var1 <- c("f1V1", "f1V2", "f1V3", "f1V4", "f1V5", "f1V6", "f1V7", "f1V8", "f1V9")
var2 <- c("f2V1", "f2V2", "f2V3", "f2V4", "f2V5", "f2V6", "f2V7", "f2V8", "f2V9")
var3 <- c("f3V1", "f3V2", "f3V3", "f3V4", "f3V5", "f3V6", "f3V7", "f3V8", "f3V9")
var4 <- c("f4V1", "f4V2", "f4V3", "f4V4", "f4V5", "f4V6", "f4V7", "f4V8", "f4V9")
var5 <- c("f5V1", "f5V2", "f5V3", "f5V4", "f5V5", "f5V6", "f5V7", "f5V8", "f5V9")
var6 <- c("f6V1", "f6V2", "f6V3", "f6V4", "f6V5", "f6V6", "f6V7", "f6V8", "f6V9")
longFacNames <- list(FU = c("DEP0","DEP1","DEP2","DEP3","DEP4","DEP5","DEP6"))
syntax.config <- measEq.syntax(configural.model = model, data = DEP_SAL, parameterization = "theta",
ID.fac = "std.lv", ID.cat = "millsap", estimator = "WLSMV",
return.fit = TRUE, longFacNames=longFacNames,
ordered = c("f0V1", "f0V2", "f0V3", "f0V4", "f0V5", "f0V6", "f0V7", "f0V8", "f0V9",
"f1V1", "f1V2", "f1V3", "f1V4", "f1V5", "f1V6", "f1V7", "f1V8", "f1V9",
"f2V1", "f2V2", "f2V3", "f2V4", "f2V5", "f2V6", "f2V7", "f2V8", "f2V9",
"f3V1", "f3V2", "f3V3", "f3V4", "f3V5", "f3V6", "f3V7", "f3V8", "f3V9",
"f4V1", "f4V2", "f4V3", "f4V4", "f4V5", "f4V6", "f4V7", "f4V8", "f4V9",
"f5V1", "f5V2", "f5V3", "f5V4", "f5V5", "f5V6", "f5V7", "f5V8", "f5V9",
"f6V1", "f6V2", "f6V3", "f6V4","f6V5", "f6V6", "f6V7", "f6V8", "f6V9"))
cat(as.character(syntax.config))
summary(syntax.config, fit.measures=TRUE, standardized=TRUE) When I mail the analysis I get this error
Error in lav_samplestats_step1(Y = Data, ov.names = ov.names, ov.types = ov.types, :
lavaan ERROR: some categories of variable `f0V8' are empty in group 1; frequencies are [1670 45 43 0]
Terrence Jorgensen
I defined the following items as ordinal and converted to numeric
Error in specify[[1]][RR, CC] : subscript out of bounds
when I check the estimator:
> unlist(lavInspect(metric, what = "Options"))["estimator"]
estimator
"DWLS"
>
I don’t get “WLSMV”, which is recommended for MGCFA with ordinal variables.
Finally, I have another doubt. I’m trying to run multiple imputed files with measEq.syntax(), but since this takes a long time with “mice”, I thought of saving the imputed data frames in a “mids” object and then running the analysis. However, I could not figure out how to do this with the help page of measEq.syntax().
set.seed(12345)
HSMiss <- HolzingerSwineford1939[ , paste("x", 1:9, sep = "")]
HSMiss$x5 <- ifelse(HSMiss$x1 <= quantile(HSMiss$x1, .3), NA, HSMiss$x5)
HSMiss$x9 <- ifelse(is.na(HSMiss$x5), NA, HSMiss$x9)
HSMiss$school <- HolzingerSwineford1939$school
HS.amelia <- amelia(HSMiss, m = 20, noms = "school")
imps <- HS.amelia$imputations
HS.model <- '
visual =~ x1 + a*x2 + b*x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
ab := a*b
'
mgfit1 <- cfa.mi(HS.model, data = imps, std.lv = TRUE, group = "school")
syntax.mi <- measEq.syntax(configural.model = mgfit1, group = "school",
group.equal = c("loadings","intercepts"))
cat(as.character(syntax.mi))
summary(syntax.mi)
## return fit
fit.mi <- measEq.syntax(configural.model = mgfit1, group = "school",
group.equal = c("loadings","intercepts"),
return.fit = TRUE)
summary(fit.mi)Terrence Jorgensen
When I mail the analysis I get this error
lavaan ERROR: some categories of variable `f0V8' are empty in group 1; frequencies are [1670 45 43 0]
Carlos Lemos
Una
ID.fac="auto.fix.first", return.fit = TRUE,
longFacNames = list(X = c("X1","X2")), auto=T,
long.equal=c("loadings","intercepts"), long.partial = c("x2.1 ~ 1","x2.2 ~ 1"))
Terrence Jorgensen
long.partial = c("x2.1 ~ 1","x2.2 ~ 1"))And this is the warning message:Warning message: In if (long.partial == "") { : the condition has length > 1 and only the first element will be usedIf I use only long.partial="x2 ~ 1", it doesn't give a warning message, but it still equals the intercepts.
Una
Terrence Jorgensen
If I understood correctly, in long.partial I can not use actual observed-variables names
I have to use a name refered to in longIndNames.
Is there maybe a way to access the automated indicator names, and then use those names when testing partial invariance?
mod.cat <- ' FU1 =~ u1 + u2 + u3 + u4
FU2 =~ u5 + u6 + u7 + u8 '
## the 2 factors are actually the same factor (FU) measured twice
longFacNames <- list(FU = c("FU1","FU2"))
## configural model: no constraints across groups or repeated measures
syntax.config <- measEq.syntax(configural.model = mod.cat, data = datCat,
ordered = paste0("u", 1:8),
parameterization = "theta",
group = "g", longFacNames = longFacNames)
## extract default longIndNames
syntax.config@call$longIndNamesmi.i@external$measEq.syntax@call$longIndNamesThank you for all the effort put in SEM tools,
Carlos Lemos
> scalar.partial <- measEq.syntax(model, data = df, ordered = indicators, parameterization = "theta",
+ ID.fac = "std.lv", ID.cat = "Wu.Estabrook.2016", estimator = "WLSMV",
+ group.partial = c("V33~1","V37~1","V48~1","ATTEND~1"), return.fit = TRUE)
Warning message:
In if (group.partial == "") { :
the condition has length > 1 and only the first element will be used
$`NO-Norway`$nu
intrcp
V30 0
V31 0
V32 0
V33 1579
V28 0
V35 0
V37 1580
V46 0
V47 0
V48 1581
V49 0
V51 0
ATTEND 1582
...
$`IT-Italy`$nu
intrcp
V30 0
V31 0
V32 0
V33 1751
V28 0
V35 0
V37 1752
V46 0
V47 0
V48 1753
V49 0
V51 0
ATTEND 1754
Terrence Jorgensen
It seems that the function is working OK
devtools::install_github("simsem/semTools/semTools")Is there any function in lavaan to test the equality of the group variance-covariance matrices (general and/or multiple pairwise)?
varnames <- paste0("x", 1:6)
## specify model parameters
covstruc <- outer(varnames, varnames, function(x, y) paste(x, "~~", y))
satMod <- c(paste(varnames, "~ 1"), # mean structure
covstruc[lower.tri(covstruc, diag = TRUE)]) # covariance structure
cat(satMod, sep = "\n")
## fit model, unconstrained across groups
fit1 <- lavaan(satMod, data = HolzingerSwineford1939, group = "school")
## fit model, all parameters constrained across groups
fit0 <- lavaan(satMod, data = HolzingerSwineford1939, group = "school",
group.equal = c("intercepts","residuals","residual.covariances"))How can I get Chi-square contributions for each group other than using summary()?
fit@test[[1]]$stat.group # naïve
fit@test[[2]]$stat.group # robust- Some authors state that 0.05 <= RMSEA < 0.08 means acceptable fit, but others (particularly Hu & Bentler (1999)) recommend 0.06 as cutoff for acceptable fit. I'm using the more restrictive limit, particularly because a recent paper warned on the use of criteria based on ML estimation for assessing fit of models with ordinal items obtained using WLSMV:
Do you know about any recent study that recommends criteria for assessing fit in measurement invariance tests of complex models with large samples and ordinal items?
Carlos Lemos
Johanna Schüller
retest.model.FPP <- 'FPP_T1 =~ "PPQ7_Emp"+ "PPQ19_Emp"+ "PPQ25_Emp"+ "PPQ31_Emp"+ "PPQ37_Emp"+"PPQ2_Furchtl"+ "PPQ8_Furchtl"+ "PPQ14_Furchtl"+ "PPQ26_Furchtl"+ "PPQ38_Furchtl"+"PPQ3_Ego"+ "PPQ9_Ego"+ "PPQ21_Ego"+ "PPQ27_Ego"+ "PPQ39_Ego"+"PPQ4_Impul"+ "PPQ10_Impul"+ "PPQ16_Impul"+ "PPQ22_Impul"+ "PPQ40_Impul"+"PPQ11_Soz"+ "PPQ17_Soz"+ "PPQ23_Soz"+ "PPQ29_Soz"+ "PPQ35_Soz" +"PPQ6_Macht" + "PPQ12_Macht"+ "PPQ18_Macht"+ "PPQ24_Macht"+ "PPQ36_Macht"FPP_T2 =~ "PPQ7_A_Emp" + "PPQ19_A_Emp" + "PPQ25_A_Emp"+ "PPQ31_A_Emp"+ "PPQ37_A_Emp" +"PPQ2_A_Furchtl"+ "PPQ8_A_Furchtl"+ "PPQ14_A_Furchtl"+ "PPQ26_A_Furchtl"+ "PPQ38_A_Furchtl"+"PPQ3_A_Ego"+ "PPQ9_A_Ego"+ "PPQ21_A_Ego"+ "PPQ27_A_Ego"+ "PPQ39_A_Ego"+"PPQ4_A_Impul"+ "PPQ10_A_Impul"+ "PPQ16_A_Impul"+ "PPQ22_A_Impul"+ "PPQ40_A_Impul"+"PPQ11_A_Soz"+ "PPQ17_A_Soz" + "PPQ23_A_Soz"+ "PPQ29_A_Soz"+ "PPQ35_A_Soz"+"PPQ6_A_Macht"+ "PPQ12_A_Macht" + "PPQ18_A_Macht"+ "PPQ24_A_Macht"+ "PPQ36_A_Macht"'var1 <- c("PPQ7_Emp", "PPQ19_Emp", "PPQ25_Emp", "PPQ31_Emp", "PPQ37_Emp","PPQ2_Furchtl", "PPQ8_Furchtl", "PPQ14_Furchtl", "PPQ26_Furchtl", "PPQ38_Furchtl","PPQ3_Ego", "PPQ9_Ego", "PPQ21_Ego", "PPQ27_Ego", "PPQ39_Ego","PPQ4_Impul", "PPQ10_Impul", "PPQ16_Impul", "PPQ22_Impul", "PPQ40_Impul","PPQ11_Soz", "PPQ17_Soz", "PPQ23_Soz", "PPQ29_Soz", "PPQ35_Soz" ,"PPQ6_Macht" , "PPQ12_Macht", "PPQ18_Macht", "PPQ24_Macht", "PPQ36_Macht")var2 <- c("PPQ7_A_Emp" , "PPQ19_A_Emp" , "PPQ25_A_Emp", "PPQ31_A_Emp", "PPQ37_A_Emp" ,"PPQ2_A_Furchtl", "PPQ8_A_Furchtl", "PPQ14_A_Furchtl", "PPQ26_A_Furchtl", "PPQ38_A_Furchtl","PPQ3_A_Ego", "PPQ9_A_Ego", "PPQ21_A_Ego", "PPQ27_A_Ego", "PPQ39_A_Ego","PPQ4_A_Impul", "PPQ10_A_Impul", "PPQ16_A_Impul", "PPQ22_A_Impul", "PPQ40_A_Impul","PPQ11_A_Soz", "PPQ17_A_Soz" , "PPQ23_A_Soz", "PPQ29_A_Soz", "PPQ35_A_Soz","PPQ6_A_Macht", "PPQ12_A_Macht" , "PPQ18_A_Macht", "PPQ24_A_Macht", "PPQ36_A_Macht")
longFacNames <- list(FU = c("FPP_T1", "FPP_T2"))measEq.syntax(retest.model.FPP_lavaan, #spezifiziertes Modell über LavaanID.fac = "std.lv", #standardisierter latenter FaktorID.cat = "Wu", #default GuidelinelongFacNames = longFacNames,return.fit = TRUE)
Terrence Jorgensen
I receive the error message:"lavaan 0.6-3 did not run (perhaps do.fit = FALSE)?** WARNING ** Estimates below are simply the starting values"
Would you help me out and tell me where I went wrong?Here is my code:retest.model.FPP <- 'FPP_T1 =~ "PPQ7_Emp"+ "PPQ19_Emp"+ "PPQ25_Emp"+ "PPQ31_Emp"+ "PPQ37_Emp"+"PPQ2_Furchtl"+ "PPQ8_Furchtl"+ "PPQ14_Furchtl"+ "PPQ26_Furchtl"+ "PPQ38_Furchtl"+"PPQ3_Ego"+ "PPQ9_Ego"+ "PPQ21_Ego"+ "PPQ27_Ego"+ "PPQ39_Ego"+"PPQ4_Impul"+ "PPQ10_Impul"+ "PPQ16_Impul"+ "PPQ22_Impul"+ "PPQ40_Impul"+"PPQ11_Soz"+ "PPQ17_Soz"+ "PPQ23_Soz"+ "PPQ29_Soz"+ "PPQ35_Soz" +"PPQ6_Macht" + "PPQ12_Macht"+ "PPQ18_Macht"+ "PPQ24_Macht"+ "PPQ36_Macht"FPP_T2 =~ "PPQ7_A_Emp" + "PPQ19_A_Emp" + "PPQ25_A_Emp"+ "PPQ31_A_Emp"+ "PPQ37_A_Emp" +"PPQ2_A_Furchtl"+ "PPQ8_A_Furchtl"+ "PPQ14_A_Furchtl"+ "PPQ26_A_Furchtl"+ "PPQ38_A_Furchtl"+"PPQ3_A_Ego"+ "PPQ9_A_Ego"+ "PPQ21_A_Ego"+ "PPQ27_A_Ego"+ "PPQ39_A_Ego"+"PPQ4_A_Impul"+ "PPQ10_A_Impul"+ "PPQ16_A_Impul"+ "PPQ22_A_Impul"+ "PPQ40_A_Impul"+"PPQ11_A_Soz"+ "PPQ17_A_Soz" + "PPQ23_A_Soz"+ "PPQ29_A_Soz"+ "PPQ35_A_Soz"+"PPQ6_A_Macht"+ "PPQ12_A_Macht" + "PPQ18_A_Macht"+ "PPQ24_A_Macht"+ "PPQ36_A_Macht"'
measEq.syntax(retest.model.FPP_lavaan, #spezifiziertes Modell über LavaanID.fac = "std.lv", #standardisierter latenter FaktorID.cat = "Wu", #default GuidelinelongFacNames = longFacNames,return.fit = TRUE)
Johanna Schüller
Jessica Fritz
# Latent common factor means
# Fix T1 common factor mean to zero
C1FAMo ~ 0*1
# Freely estimate T2-T4 common factor means
C2FAMo ~ 1
C3FAMo ~ 1
C4FAMo ~ 1
## LATENT MEANS/INTERCEPTS:
FS_early ~ alpha.1*1 + NA*1
FS_late ~ alpha.2*1 + NA*1FS_late =~ RF1FQ1_occ2 + RF1FQ2_occ2 + RF1FQ3_occ2 + RF1FQ4_occ2 + RF1FQ8_occ2'
longFacNames <- list(FS = c("FS_early","FS_late")); longFacNames
longIndNames <- list(RF1FQ1 = c("RF1FQ1_occ1","RF1FQ1_occ2"),
RF1FQ2 = c("RF1FQ2_occ1","RF1FQ2_occ2"),
RF1FQ3 = c("RF1FQ3_occ1","RF1FQ3_occ2"),
RF1FQ4 = c("RF1FQ4_occ1","RF1FQ4_occ2"),
RF1FQ8 = c("RF1FQ8_occ1","RF1FQ8_occ2")); longIndNames
#Run configural model
syntax.fit.F_Model_T <- measEq.syntax(configural.model = F_Model,
data = F_Data,
estimator="WLSMV",
ordered=c("RF1FQ1_occ1", "RF1FQ2_occ1", "RF1FQ3_occ1", "RF1FQ4_occ1", "RF1FQ8_occ1",
"RF1FQ1_occ2", "RF1FQ2_occ2", "RF1FQ3_occ2", "RF1FQ4_occ2", "RF1FQ8_occ2"),
parameterization = "theta",
ID.fac = "UL",
ID.cat = "millsap.tein.2004",
longFacNames = longFacNames,
longIndNames = longIndNames,
auto = "all")
cat(as.character(syntax.fit.F_Model_T))
summary(syntax.fit.F_Model_T)
On Sunday, August 26, 2018 at 11:02:43 PM UTC+1, Terrence Jorgensen wrote:
Terrence Jorgensen
This is my correct code:library(semTools)retest.model.FPP_lavaan <- 'FPP_T1 =~ "PPQ7_Emp"+ "PPQ19_Emp"+ "PPQ25_Emp"+ "PPQ31_Emp"+ "PPQ37_Emp"+"PPQ2_Furchtl"+ "PPQ8_Furchtl"+ "PPQ14_Furchtl"+ "PPQ26_Furchtl"+ "PPQ38_Furchtl"+"PPQ3_Ego"+ "PPQ9_Ego"+ "PPQ21_Ego"+ "PPQ27_Ego"+ "PPQ39_Ego"+"PPQ4_Impul"+ "PPQ10_Impul"+ "PPQ16_Impul"+ "PPQ22_Impul"+ "PPQ40_Impul"+"PPQ11_Soz"+ "PPQ17_Soz"+ "PPQ23_Soz"+ "PPQ29_Soz"+ "PPQ35_Soz" +"PPQ6_Macht" + "PPQ12_Macht"+ "PPQ18_Macht"+ "PPQ24_Macht"+ "PPQ36_Macht"FPP_T2 =~ "PPQ7_A_Emp" + "PPQ19_A_Emp" + "PPQ25_A_Emp"+ "PPQ31_A_Emp"+ "PPQ37_A_Emp" +"PPQ2_A_Furchtl"+ "PPQ8_A_Furchtl"+ "PPQ14_A_Furchtl"+ "PPQ26_A_Furchtl"+ "PPQ38_A_Furchtl"+"PPQ3_A_Ego"+ "PPQ9_A_Ego"+ "PPQ21_A_Ego"+ "PPQ27_A_Ego"+ "PPQ39_A_Ego"+"PPQ4_A_Impul"+ "PPQ10_A_Impul"+ "PPQ16_A_Impul"+ "PPQ22_A_Impul"+ "PPQ40_A_Impul"+"PPQ11_A_Soz"+ "PPQ17_A_Soz" + "PPQ23_A_Soz"+ "PPQ29_A_Soz"+ "PPQ35_A_Soz"+"PPQ6_A_Macht"+ "PPQ12_A_Macht" + "PPQ18_A_Macht"+ "PPQ24_A_Macht"+ "PPQ36_A_Macht"'
retest.model.FPP_lavaan <- '
FPP_T1 =~ PPQ7_Emp+ PPQ19_Emp+ PPQ25_Emp+ PPQ31_Emp+ PPQ37_Emp+
PPQ2_Furchtl+ PPQ8_Furchtl+ PPQ14_Furchtl+ PPQ26_Furchtl+ PPQ38_Furchtl+
PPQ3_Ego+ PPQ9_Ego+ PPQ21_Ego+ PPQ27_Ego+ PPQ39_Ego+
PPQ4_Impul+ PPQ10_Impul+ PPQ16_Impul+ PPQ22_Impul+ PPQ40_Impul+
PPQ11_Soz+ PPQ17_Soz+ PPQ23_Soz+ PPQ29_Soz+ PPQ35_Soz +
PPQ6_Macht + PPQ12_Macht+ PPQ18_Macht+ PPQ24_Macht+ PPQ36_Macht
FPP_T2 =~ PPQ7_A_Emp + PPQ19_A_Emp + PPQ25_A_Emp+ PPQ31_A_Emp+ PPQ37_A_Emp +
PPQ2_A_Furchtl+ PPQ8_A_Furchtl+ PPQ14_A_Furchtl+ PPQ26_A_Furchtl+ PPQ38_A_Furchtl+
PPQ3_A_Ego+ PPQ9_A_Ego+ PPQ21_A_Ego+ PPQ27_A_Ego+ PPQ39_A_Ego+
PPQ4_A_Impul+ PPQ10_A_Impul+ PPQ16_A_Impul+ PPQ22_A_Impul+ PPQ40_A_Impul+
PPQ11_A_Soz+ PPQ17_A_Soz + PPQ23_A_Soz+ PPQ29_A_Soz+ PPQ35_A_Soz+
PPQ6_A_Macht+ PPQ12_A_Macht + PPQ18_A_Macht+ PPQ24_A_Macht+ PPQ36_A_Macht
'retest.model.FPP_lavaan <- c(paste("FPP_T1 =~", var1), paste("FPP_T2 =~", var2))retest.model.FPP_lavaan <- c(paste("FPP_T1 =~", var1), paste("FPP_T2 =~", var2),
"PPQ24_A_Macht ~~ PPQ36_A_Macht")Terrence Jorgensen
when I try to replicate the syntax with measEq.syntax() (as shown below) the first mean is not fixed to zero but is freely estimated:## LATENT MEANS/INTERCEPTS:
FS_early ~ alpha.1*1 + NA*1 FS_late ~ alpha.2*1 + NA*1
devtools::install_github("simsem/semTools/semTools")Jessica Fritz
Pavneet Kaur
Hello Dr. Terrence.
First of all, Thanks for this measEq.syntax() function as it is really helpful.
I have a doubt regarding the group.equal ( ), as stated underneath:
type5 <- 't5=~ g4q1.5+ g4q3.5+ g4q5.5 + g4q7.5 + g5q1.5+ g5q3.5+ g5q5.5 + g5q7.5
g5q1.5 ~~ g5q5.5'
After testing invariance for threshold and loadings, using group.partial ( ) for one indicator, the fit indices for latent-varaible invariance is given as:
test_th.lo.var<-measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal=c("thresholds","loadings","lv.variances"), group.partial = c("type5=~g5q3.5","g5q3.5|t1"), warn=T, return.fit=T, ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5", "g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"), parameterization="theta", estimator="wlsmv", meanstructure=TRUE)
chisq.scaled df.scaled pvalue.scaled cfi.scaled rmsea.scaled tli.scaled
#63.048 46.000 0.048 0.955 0.020 0.945
Now, I am interested in testing the invariance of latent-variable means , but it is yielding the same fit-indices as above:
test_th.lo.var.means<-measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal=c("thresholds","loadings","lv.variances","means"), warn=T, return.fit=T, ordered = c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5", "g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"), parameterization = "theta", estimator="wlsmv", meanstructure=TRUE)
#chisq.scaled df.scaled pvalue.scaled cfi.scaled rmsea.scaled tli.scaled
#63.048 46.000 0.048 0.955 0.020 0.945
I am unsure why these two fit-indices are same, though the “test_th.lo.var.means” has means set to be equal on both groups? Thanks in advance,
Pavneet Kaur
Terrence Jorgensen
group.equal=c("thresholds","loadings","lv.variances","means")
I am unsure why these two fit-indices are same, though the “test_th.lo.var.means” has means set to be equal on both groups?
Pavneet Bharaj
Thanks Professor Terrence for your reply back. That was useful.
I have fixed the “intercepts” to be equal in group.equal argument, but even them I am having the same issue.
I am wondering as group.equal for “means” provided a different fit index for model “t2”, but not “t5”. Even if all the indices remain same, I would expect a change in degrees of freedom. Please let me know if I am doing something wrong in the given code:
type5 <- 't5=~ g4q1.5+ g4q3.5+ g4q5.5 + g4q7.5 + g5q1.5+ g5q3.5+ g5q5.5 + g5q7.5
g5q1.5 ~~ g5q5.5'
#===== CHECKING EQUAL VARIANCES ========#
test_th.lo.var<-measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("loadings","thresholds", "intercepts", "lv.variances"),
warn=T, return.fit=T,
ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5",
"g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE)
summary(test_th.lo.var, fit.measures=T, rsquare=T)
#chisq.scaled df.scaled pvalue.scaled cfi.scaled rmsea.scaled tli.scaled
#62.004 46.000 0.058 0.957 0.019 0.948
#===== CHECKING EQUAL MEANS ========#
test_th.lo.var.means<-measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal=c("loadings","thresholds", "intercepts", "lv.variances","means"), warn=T, return.fit=T,
ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5",
"g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE)
summary(test_th.lo.var.means, fit.measures=T, rsquare=T)
#chisq.scaled df.scaled pvalue.scaled cfi.scaled rmsea.scaled tli.scaled
# 62.004 46.000 0.058 0.957 0.019 0.948
#==============================#
type2 <- 'type2=~ g4q1.2+ g4q3.2+ g4q5.2+ g4q7.2+ g5q1.2+ g5q3.2+ g5q5.2+ g5q7.2
g4q3.2 ~~ g5q5.2
g5q1.2 ~~ g5q5.2'
#===== CHECKING EQUAL VARIANCES ========#
test_partial_th.lo2.var<-measEq.syntax(type2, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("thresholds","loadings", "intercepts","lv.variances"),
group.partial=c("type2=~g5q3.2","g5q3.2|t1"),warn=T, return.fit=T,
ordered=c("g4q1.2", "g4q3.2", "g4q5.2", "g4q7.2",
"g5q1.2", "g5q3.2", "g5q5.2", "g5q7.2"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE)
summary(test_partial_th.lo2.var, fit.measures=T, rsquare=T)
#chisq.scaled df.scaled pvalue.scaled cfi.scaled rmsea.scaled tli.scaled
# 48.741 43.000 0.253 0.954 0.012 0.940
#===== CHECKING EQUAL MEANS ========#
test_partial_th.lo2_var.means<-measEq.syntax(type2, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("thresholds","loadings","intercepts", "lv.variances", "means"), warn=T, return.fit=T,
ordered=c("g4q1.2", "g4q3.2", "g4q5.2", "g4q7.2",
"g5q1.2", "g5q3.2", "g5q5.2", "g5q7.2"),
parameterization="theta", estimator="wlsmv", meanstructure=TRUE)
summary(test_partial_th.lo2_var.means, fit.measures=T, rsquare=T)
#chisq.scaled df.scaled pvalue.scaled cfi.scaled rmsea.scaled tli.scaled
# 55.472 44.000 0.115 0.909 0.017 0.884
Terrence Jorgensen
I have fixed the “intercepts” to be equal in group.equal argument, but even them I am having the same issue.
devtools::install_github("simsem/semTools/semTools")I am wondering as group.equal for “means” provided a different fit index for model “t2”, but not “t5”.
Pavneet Bharaj
I have fixed the “intercepts” to be equal in group.equal argument, but even them I am having the same issue.
Do you have the issue after installing the latest development version of semTools?
devtools::install_github("simsem/semTools/semTools")
Yeah, the issue is still there, even though I have installed semTools again using above code.
If so, I suggest you leave return.fit=FALSE so you can inspect the model syntax to see what is happening. For example, does adding "means" to group.equal= not lose a df because the means are already constrained in the model without "means" in group.equal=? Or because adding "means" to group.equal= does not give them the same labels to add the equality constraint, or because the means are not free parameters? This will help me figure out if I need to update the function.
So, I tried to use fit.measure=F and to clarify I am providing the syntax and results underneath:
Return.fit=FALSE
test_th.lo.var <- measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("thresholds","loadings", "lv.variances"),
warn=T, return.fit=F,
ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5",
"g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE)
summary(test_th.lo.var)
output:
This lavaan model syntax specifies a CFA with 8 manifest indicators (8 of which are ordinal) of 1 common factor(s).
To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed.
The location and scale of each latent item-response underlying 8 ordinal indicators were identified using the "theta" parameterization, and the identification constraints recommended by Wu & Estabrook (2016). For details, read:
https://doi.org/10.1007/s11336-016-9506-0
Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor:
t5
g4q1.5 ord
g4q3.5 ord
g4q5.5 ord
g4q7.5 ord
g5q1.5 ord
g5q3.5 ord
g5q5.5 ord
g5q7.5 ord
The following types of parameter were constrained to equality across groups:
thresholds
loadings
lv.variances
test_th.lo.var.means <- measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("thresholds","loadings","lv.variances","means"),
warn=T, return.fit=F,
ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5",
"g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE)
summary(test_th.lo.var.means)
OUTPUT:
This lavaan model syntax specifies a CFA with 8 manifest indicators (8 of which are ordinal) of 1 common factor(s). To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed. The location and scale of each latent item-response underlying 8 ordinal indicators were identified using the "theta" parameterization, and the identification constraints recommended by Wu & Estabrook (2016). For details, read: https://doi.org/10.1007/s11336-016-9506-0 Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor: t5 g4q1.5 ordg4q3.5 ordg4q5.5 ordg4q7.5 ordg5q1.5 ordg5q3.5 ordg5q5.5 ordg5q7.5 ord The following types of parameter were constrained to equality across groups: thresholds loadings lv.variances means
Syntax and output with fit.measure=T
test_th.lo.var<-measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("thresholds","loadings", "lv.variances"),
warn=T, return.fit=T,
ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5",
"g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE)
summary(test_th.lo.var, fit.measures=T, rsquare=T)
lavaan 0.6-3 ended normally after 57 iterations Optimization method NLMINB Number of free parameters 42Number of equality constraints 16
Number of observations per group 0 919 1 926 Estimator DWLS Robust Model Fit Test Statistic 59.510 63.048 Degrees of freedom 46 46 P-value (Chi-square) 0.087 0.048 Scaling correction factor 0.943 Shift parameter for each group: 0 -0.018 1 -0.018 for simple second-order correction (Mplus variant) Chi-square for each group: 0 34.682 36.748 1 24.827 26.301 Model test baseline model: Minimum Function Test Statistic 466.605 432.226 Degrees of freedom 56 56 P-value 0.000 0.000 User model versus baseline model: Comparative Fit Index (CFI) 0.967 0.955 Tucker-Lewis Index (TLI) 0.960 0.945 Robust Comparative Fit Index (CFI) NA Robust Tucker-Lewis Index (TLI) NA Root Mean Square Error of Approximation: RMSEA 0.018 0.020 90 Percent Confidence Interval 0.000 0.030 0.002 0.031 P-value RMSEA <= 0.05 1.000 1.000 Robust RMSEA NA 90 Percent Confidence Interval NA NA Standardized Root Mean Square Residual: SRMR 0.073 0.073 Parameter Estimates: Information Expected Information saturated (h1) model Unstructured Standard Errors Robust.sem Group 1 [0]: Latent Variables: Estimate Std.Err z-value P(>|z|) t5 =~ g4q1.5 (l.1_) 0.555 0.065 8.508 0.000 g4q3.5 (l.2_) 1.013 0.143 7.076 0.000 g4q5.5 (l.3_) 0.601 0.071 8.412 0.000 g4q7.5 (l.4_) 0.273 0.110 2.471 0.013 g5q1.5 (l.5_) 0.264 0.048 5.540 0.000 g5q3.5 (l.6_) -0.019 0.043 -0.452 0.652 g5q5.5 (l.7_) 0.377 0.065 5.803 0.000 g5q7.5 (l.8_) -0.149 0.044 -3.389 0.001 Covariances: Estimate Std.Err z-value P(>|z|) .g5q1.5 ~~ .g5q5.5 (t.7_) 0.173 0.077 2.255 0.024 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.5 (n.1.) 0.000 .g4q3.5 (n.2.) 0.000 .g4q5.5 (n.3.) 0.000 .g4q7.5 (n.4.) 0.000 .g5q1.5 (n.5.) 0.000 .g5q3.5 (n.6.) 0.000 .g5q5.5 (n.7.) 0.000 .g5q7.5 (n.8.) 0.000 t5 (a.1.) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.5|1 (g41.) 0.638 0.053 12.151 0.000 g43.5|1 (g43.) 0.581 0.073 7.932 0.000 g45.5|1 (g45.) -0.364 0.050 -7.239 0.000 g47.5|1 (g47.) 2.188 0.118 18.611 0.000 g51.5|1 (g51.) -0.132 0.043 -3.064 0.002 g53.5|1 (g53.) -0.094 0.041 -2.275 0.023 g55.5|1 (g55.) 1.349 0.066 20.578 0.000 g57.5|1 (g57.) -0.087 0.042 -2.077 0.038 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.5 (t.1_) 1.000 .g4q3.5 (t.2_) 1.000 .g4q5.5 (t.3_) 1.000 .g4q7.5 (t.4_) 1.000 .g5q1.5 (t.5_) 1.000 .g5q3.5 (t.6_) 1.000 .g5q5.5 (t.7_) 1.000 .g5q7.5 (t.8_) 1.000 t5 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.5 0.875 g4q3.5 0.703 g4q5.5 0.857 g4q7.5 0.965 g5q1.5 0.967 g5q3.5 1.000 g5q5.5 0.936 g5q7.5 0.989 R-Square: Estimate g4q1.5 0.235 g4q3.5 0.506 g4q5.5 0.265 g4q7.5 0.069 g5q1.5 0.065 g5q3.5 0.000 g5q5.5 0.125 g5q7.5 0.022 Group 2 [1]: Latent Variables: Estimate Std.Err z-value P(>|z|) t5 =~ g4q1.5 (l.1_) 0.555 0.065 8.508 0.000 g4q3.5 (l.2_) 1.013 0.143 7.076 0.000 g4q5.5 (l.3_) 0.601 0.071 8.412 0.000 g4q7.5 (l.4_) 0.273 0.110 2.471 0.013 g5q1.5 (l.5_) 0.264 0.048 5.540 0.000 g5q3.5 (l.6_) -0.019 0.043 -0.452 0.652 g5q5.5 (l.7_) 0.377 0.065 5.803 0.000 g5q7.5 (l.8_) -0.149 0.044 -3.389 0.001 Covariances: Estimate Std.Err z-value P(>|z|) .g5q1.5 ~~ .g5q5.5 (t.7_) 0.154 0.067 2.289 0.022 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.5 (n.1.) -0.044 0.071 -0.619 0.536 .g4q3.5 (n.2.) 0.085 0.086 0.997 0.319 .g4q5.5 (n.3.) 0.046 0.070 0.655 0.513 .g4q7.5 (n.4.) 0.022 0.145 0.154 0.878 .g5q1.5 (n.5.) -0.025 0.061 -0.412 0.680 .g5q3.5 (n.6.) 0.025 0.059 0.430 0.667 .g5q5.5 (n.7.) 0.328 0.080 4.114 0.000 .g5q7.5 (n.8.) -0.040 0.059 -0.684 0.494 t5 (a.1.) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.5|1 (g41.) 0.638 0.053 12.151 0.000 g43.5|1 (g43.) 0.581 0.073 7.932 0.000 g45.5|1 (g45.) -0.364 0.050 -7.239 0.000 g47.5|1 (g47.) 2.188 0.118 18.611 0.000 g51.5|1 (g51.) -0.132 0.043 -3.064 0.002 g53.5|1 (g53.) -0.094 0.041 -2.275 0.023 g55.5|1 (g55.) 1.349 0.066 20.578 0.000 g57.5|1 (g57.) -0.087 0.042 -2.077 0.038 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.5 (t.1_) 1.000 .g4q3.5 (t.2_) 1.000 .g4q5.5 (t.3_) 1.000 .g4q7.5 (t.4_) 1.000 .g5q1.5 (t.5_) 1.000 .g5q3.5 (t.6_) 1.000 .g5q5.5 (t.7_) 1.000 .g5q7.5 (t.8_) 1.000 t5 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.5 0.875 g4q3.5 0.703 g4q5.5 0.857 g4q7.5 0.965 g5q1.5 0.967 g5q3.5 1.000 g5q5.5 0.936 g5q7.5 0.989 R-Square: Estimate g4q1.5 0.235 g4q3.5 0.506 g4q5.5 0.265 g4q7.5 0.069 g5q1.5 0.065 g5q3.5 0.000 g5q5.5 0.125 g5q7.5 0.022
test_th.lo.var.means<-measEq.syntax(type5, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("thresholds","loadings","lv.variances","means"),
warn=T, return.fit=T,
ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5",
"g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE)
summary(test_th.lo.var.means, fit.measures=T, rsquare=T)
lavaan 0.6-3 ended normally after 57 iterations Optimization method NLMINB Number of free parameters 42Number of equality constraints 16
Number of observations per group 0 919 1 926 Estimator DWLS Robust Model Fit Test Statistic 59.510 63.048 Degrees of freedom 46 46 P-value (Chi-square) 0.087 0.048 Scaling correction factor 0.943 Shift parameter for each group: 0 -0.018 1 -0.018 for simple second-order correction (Mplus variant) Chi-square for each group: 0 34.682 36.748 1 24.827 26.301 Model test baseline model: Minimum Function Test Statistic 466.605 432.226 Degrees of freedom 56 56 P-value 0.000 0.000 User model versus baseline model: Comparative Fit Index (CFI) 0.967 0.955 Tucker-Lewis Index (TLI) 0.960 0.945 Robust Comparative Fit Index (CFI) NA Robust Tucker-Lewis Index (TLI) NA Root Mean Square Error of Approximation: RMSEA 0.018 0.020 90 Percent Confidence Interval 0.000 0.030 0.002 0.031 P-value RMSEA <= 0.05 1.000 1.000 Robust RMSEA NA 90 Percent Confidence Interval NA NA Standardized Root Mean Square Residual: SRMR 0.073 0.073 Parameter Estimates: Information Expected Information saturated (h1) model Unstructured Standard Errors Robust.sem Group 1 [0]: Latent Variables: Estimate Std.Err z-value P(>|z|) t5 =~ g4q1.5 (l.1_) 0.555 0.065 8.508 0.000 g4q3.5 (l.2_) 1.013 0.143 7.076 0.000 g4q5.5 (l.3_) 0.601 0.071 8.412 0.000 g4q7.5 (l.4_) 0.273 0.110 2.471 0.013 g5q1.5 (l.5_) 0.264 0.048 5.540 0.000 g5q3.5 (l.6_) -0.019 0.043 -0.452 0.652 g5q5.5 (l.7_) 0.377 0.065 5.803 0.000 g5q7.5 (l.8_) -0.149 0.044 -3.389 0.001 Covariances: Estimate Std.Err z-value P(>|z|) .g5q1.5 ~~ .g5q5.5 (t.7_) 0.173 0.077 2.255 0.024 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.5 (n.1.) 0.000 .g4q3.5 (n.2.) 0.000 .g4q5.5 (n.3.) 0.000 .g4q7.5 (n.4.) 0.000 .g5q1.5 (n.5.) 0.000 .g5q3.5 (n.6.) 0.000 .g5q5.5 (n.7.) 0.000 .g5q7.5 (n.8.) 0.000 t5 (al.1) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.5|1 (g41.) 0.638 0.053 12.151 0.000 g43.5|1 (g43.) 0.581 0.073 7.932 0.000 g45.5|1 (g45.) -0.364 0.050 -7.239 0.000 g47.5|1 (g47.) 2.188 0.118 18.611 0.000 g51.5|1 (g51.) -0.132 0.043 -3.064 0.002 g53.5|1 (g53.) -0.094 0.041 -2.275 0.023 g55.5|1 (g55.) 1.349 0.066 20.578 0.000 g57.5|1 (g57.) -0.087 0.042 -2.077 0.038 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.5 (t.1_) 1.000 .g4q3.5 (t.2_) 1.000 .g4q5.5 (t.3_) 1.000 .g4q7.5 (t.4_) 1.000 .g5q1.5 (t.5_) 1.000 .g5q3.5 (t.6_) 1.000 .g5q5.5 (t.7_) 1.000 .g5q7.5 (t.8_) 1.000 t5 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.5 0.875 g4q3.5 0.703 g4q5.5 0.857 g4q7.5 0.965 g5q1.5 0.967 g5q3.5 1.000 g5q5.5 0.936 g5q7.5 0.989 R-Square: Estimate g4q1.5 0.235 g4q3.5 0.506 g4q5.5 0.265 g4q7.5 0.069 g5q1.5 0.065 g5q3.5 0.000 g5q5.5 0.125 g5q7.5 0.022 Group 2 [1]: Latent Variables: Estimate Std.Err z-value P(>|z|) t5 =~ g4q1.5 (l.1_) 0.555 0.065 8.508 0.000 g4q3.5 (l.2_) 1.013 0.143 7.076 0.000 g4q5.5 (l.3_) 0.601 0.071 8.412 0.000 g4q7.5 (l.4_) 0.273 0.110 2.471 0.013 g5q1.5 (l.5_) 0.264 0.048 5.540 0.000 g5q3.5 (l.6_) -0.019 0.043 -0.452 0.652 g5q5.5 (l.7_) 0.377 0.065 5.803 0.000 g5q7.5 (l.8_) -0.149 0.044 -3.389 0.001 Covariances: Estimate Std.Err z-value P(>|z|) .g5q1.5 ~~ .g5q5.5 (t.7_) 0.154 0.067 2.289 0.022 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.5 (n.1.) -0.044 0.071 -0.619 0.536 .g4q3.5 (n.2.) 0.085 0.086 0.997 0.319 .g4q5.5 (n.3.) 0.046 0.070 0.655 0.513 .g4q7.5 (n.4.) 0.022 0.145 0.154 0.878 .g5q1.5 (n.5.) -0.025 0.061 -0.412 0.680 .g5q3.5 (n.6.) 0.025 0.059 0.430 0.667 .g5q5.5 (n.7.) 0.328 0.080 4.114 0.000 .g5q7.5 (n.8.) -0.040 0.059 -0.684 0.494 t5 (al.1) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.5|1 (g41.) 0.638 0.053 12.151 0.000 g43.5|1 (g43.) 0.581 0.073 7.932 0.000 g45.5|1 (g45.) -0.364 0.050 -7.239 0.000 g47.5|1 (g47.) 2.188 0.118 18.611 0.000 g51.5|1 (g51.) -0.132 0.043 -3.064 0.002 g53.5|1 (g53.) -0.094 0.041 -2.275 0.023 g55.5|1 (g55.) 1.349 0.066 20.578 0.000 g57.5|1 (g57.) -0.087 0.042 -2.077 0.038 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.5 (t.1_) 1.000 .g4q3.5 (t.2_) 1.000 .g4q5.5 (t.3_) 1.000 .g4q7.5 (t.4_) 1.000 .g5q1.5 (t.5_) 1.000 .g5q3.5 (t.6_) 1.000 .g5q5.5 (t.7_) 1.000 .g5q7.5 (t.8_) 1.000 t5 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.5 0.875 g4q3.5 0.703 g4q5.5 0.857 g4q7.5 0.965 g5q1.5 0.967 g5q3.5 1.000 g5q5.5 0.936 g5q7.5 0.989 R-Square: Estimate g4q1.5 0.235 g4q3.5 0.506 g4q5.5 0.265 g4q7.5 0.069 g5q1.5 0.065 g5q3.5 0.000 g5q5.5 0.125 g5q7.5 0.022
I am wondering as group.equal for “means” provided a different fit index for model “t2”, but not “t5”.
The change occurred for type2 because you only included group.partial=c("type2=~g5q3.2","g5q3.2|t1") in the model without means constrained, not when means were constrained.
Thanks for pointing this mistake out. I have corrected it. and now I have the same problem for t2 model also as I had with t5.
Pavneet Bharaj
Do
you have the issue after installing the latest development version of semTools?
devtools::install_github("simsem/semTools/semTools")
Yeah, the issue is still there, even though I have installed semTools again using above code.
If so, I suggest you leave return.fit=FALSE so you can inspect the model syntax to see what is happening. For example, does adding "means" to group.equal= not lose a df because the means are already constrained in the model without "means" in group.equal=? Or because adding "means" to group.equal= does not give them the same labels to add the equality constraint, or because the means are not free parameters? This will help me figure out if I need to update the function.
So, I tried to use fit.measure=F and to clarify I am providing the syntax and results underneath:
> test_partial_th.lo.var<-measEq.syntax(type2, data=data, ID.cat="Wu.Estabrook.2016",group="group", group.equal=c("thresholds","loadings", "intercepts","lv.variances"), group.partial=c("type2=~g5q3.2","g5q3.2|t1"),warn=T, return.fit=F, ordered=c("g4q1.2", "g4q3.2", "g4q5.2", "g4q7.2", "g5q1.2", "g5q3.2", "g5q5.2", "g5q7.2"),parameterization="theta", estimator="wlsmv",meanstructure=TRUE)
> summary(test_partial_th.lo.var)
This lavaan model syntax specifies a CFA with 8 manifest indicators (8 of which are ordinal) of 1 common factor(s). To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed. The location and scale of each latent item-response underlying 8 ordinal indicators were identified using the "theta" parameterization, and the identification constraints recommended by Wu & Estabrook (2016). For details, read: https://doi.org/10.1007/s11336-016-9506-0 Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor: type2g4q1.2 ord g4q3.2 ord g4q5.2 ord g4q7.2 ord g5q1.2 ord g5q3.2 ord g5q5.2 ord g5q7.2 ord The following types of parameter were constrained to equality across groups: thresholds, with the exception of: lhs op rhs row-2: g5q3.2 | t1 loadings, with the exception of: lhs op rhs row-1: type2 =~ g5q3.2 intercepts lv.variances
> test_partial_th.lo_var.means<-measEq.syntax(type2, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal=c("thresholds","loadings","intercepts","lv.variances","means"),warn=T, return.fit=F, group.partial=c("type2=~g5q3.2","g5q3.2|t1"),ordered=c("g4q1.2", "g4q3.2", "g4q5.2", "g4q7.2", "g5q1.2", "g5q3.2", "g5q5.2", "g5q7.2"), parameterization="theta", estimator="wlsmv",meanstructure=TRUE)
> summary(test_partial_th.lo_var.means)
This lavaan model syntax specifies a CFA with 8 manifest indicators (8 of which are ordinal) of 1 common factor(s). To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed. The location and scale of each latent item-response underlying 8 ordinal indicators were identified using the "theta" parameterization, and the identification constraints recommended by Wu & Estabrook (2016). For details, read: https://doi.org/10.1007/s11336-016-9506-0 Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor: type2g4q1.2 ord g4q3.2 ord g4q5.2 ord g4q7.2 ord g5q1.2 ord g5q3.2 ord g5q5.2 ord g5q7.2 ord The following types of parameter were constrained to equality across groups: thresholds, with the exception of: lhs op rhs row-2: g5q3.2 | t1 loadings, with the exception of: lhs op rhs row-1: type2 =~ g5q3.2 intercepts lv.variances means
Syntax and output with fit.measure=T
> test_partial_th.lo.var<-measEq.syntax(type2, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal=c("thresholds","loadings", "intercepts","lv.variances"),group.partial=c("type2=~g5q3.2","g5q3.2|t1"),warn=T, return.fit=T, ordered=c("g4q1.2", "g4q3.2", "g4q5.2", "g4q7.2", "g5q1.2", "g5q3.2", "g5q5.2", "g5q7.2"),parameterization="theta", estimator="wlsmv",meanstructure=TRUE)
> summary(test_partial_th.lo.var, fit.measures=T, rsquare=T)
lavaan 0.6-3 ended normally after 133 iterations Optimization method NLMINB Number of free parameters 43Number of equality constraints 14
Number of observations per group 0 919 1 926 Estimator DWLS Robust Model Fit Test Statistic 46.194 48.741 Degrees of freedom 43 43 P-value (Chi-square) 0.342 0.253 Scaling correction factor 0.926 Shift parameter for each group: 0 -0.558 1 -0.563 for simple second-order correction (Mplus variant) Chi-square for each group: 0 27.350 28.963 1 18.844 19.778 Model test baseline model: Minimum Function Test Statistic 187.590 181.463 Degrees of freedom 56 56 P-value 0.000 0.000 User model versus baseline model: Comparative Fit Index (CFI) 0.976 0.954 Tucker-Lewis Index (TLI) 0.968 0.940 Robust Comparative Fit Index (CFI) NA Robust Tucker-Lewis Index (TLI) NA Root Mean Square Error of Approximation: RMSEA 0.009 0.012 90 Percent Confidence Interval 0.000 0.025 0.000 0.026 P-value RMSEA <= 0.05 1.000 1.000 Robust RMSEA NA 90 Percent Confidence Interval 0.000 NA Standardized Root Mean Square Residual: SRMR 0.055 0.055 Parameter Estimates: Information Expected Information saturated (h1) model Unstructured Standard Errors Robust.sem Group 1 [0]: Latent Variables: Estimate Std.Err z-value P(>|z|) type2 =~ g4q1.2 (l.1_) 0.361 0.076 4.754 0.000 g4q3.2 (l.2_) 0.043 0.055 0.782 0.434 g4q5.2 (l.3_) 0.683 0.178 3.831 0.000 g4q7.2 (l.4_) 0.302 0.065 4.660 0.000 g5q1.2 (l.5_) 0.226 0.076 2.954 0.003 g5q3.2 (l.6_) 0.122 0.075 1.618 0.106 g5q5.2 (l.7_) 0.304 0.088 3.463 0.001 g5q7.2 (l.8_) 0.230 0.082 2.815 0.005 Covariances: Estimate Std.Err z-value P(>|z|) .g4q3.2 ~~ .g5q5.2 (t.7_2) -0.152 0.055 -2.744 0.006 .g5q1.2 ~~ .g5q5.2 (t.7_5) -0.118 0.072 -1.652 0.099 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.2 (nu.1) 0.000 .g4q3.2 (nu.2) 0.000 .g4q5.2 (nu.3) 0.000 .g4q7.2 (nu.4) 0.000 .g5q1.2 (nu.5) 0.000 .g5q3.2 (nu.6) 0.000 .g5q5.2 (nu.7) 0.000 .g5q7.2 (nu.8) 0.000 type2 (a.1.) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.2|1 (g41.) 0.389 0.046 8.440 0.000 g43.2|1 (g43.) -0.239 0.042 -5.725 0.000 g45.2|1 (g45.) -0.017 0.038 -0.451 0.652 g47.2|1 (g47.) -0.352 0.044 -7.974 0.000 g51.2|1 (g51.) 1.071 0.056 19.269 0.000 g53.2|1 (g53.) 0.481 0.044 11.027 0.000 g55.2|1 (g55.) 0.071 0.038 1.863 0.062 g57.2|1 (g57.) 1.331 0.062 21.307 0.000 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.2 (t.1_) 1.000 .g4q3.2 (t.2_) 1.000 .g4q5.2 (t.3_) 1.000 .g4q7.2 (t.4_) 1.000 .g5q1.2 (t.5_) 1.000 .g5q3.2 (t.6_) 1.000 .g5q5.2 (t.7_) 1.000 .g5q7.2 (t.8_) 1.000 type2 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.2 0.941 g4q3.2 0.999 g4q5.2 0.826 g4q7.2 0.957 g5q1.2 0.975 g5q3.2 0.993 g5q5.2 0.957 g5q7.2 0.975 R-Square: Estimate g4q1.2 0.115 g4q3.2 0.002 g4q5.2 0.318 g4q7.2 0.084 g5q1.2 0.048 g5q3.2 0.015 g5q5.2 0.084 g5q7.2 0.050 Group 2 [1]: Latent Variables: Estimate Std.Err z-value P(>|z|) type2 =~ g4q1.2 (l.1_) 0.361 0.076 4.754 0.000 g4q3.2 (l.2_) 0.043 0.055 0.782 0.434 g4q5.2 (l.3_) 0.683 0.178 3.831 0.000 g4q7.2 (l.4_) 0.302 0.065 4.660 0.000 g5q1.2 (l.5_) 0.226 0.076 2.954 0.003 g5q3.2 (l.6_) 0.398 0.101 3.940 0.000 g5q5.2 (l.7_) 0.304 0.088 3.463 0.001 g5q7.2 (l.8_) 0.230 0.082 2.815 0.005 Covariances: Estimate Std.Err z-value P(>|z|) .g4q3.2 ~~ .g5q5.2 (t.7_2) -0.282 0.177 -1.595 0.111 .g5q1.2 ~~ .g5q5.2 (t.7_5) -0.227 0.158 -1.441 0.150 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.2 (nu.1) 0.000 .g4q3.2 (nu.2) 0.000 .g4q5.2 (nu.3) 0.000 .g4q7.2 (nu.4) 0.000 .g5q1.2 (nu.5) 0.000 .g5q3.2 (nu.6) 0.000 .g5q5.2 (nu.7) 0.000 .g5q7.2 (nu.8) 0.000 type2 (a.1.) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.2|1 (g41.) 0.389 0.046 8.440 0.000 g43.2|1 (g43.) -0.239 0.042 -5.725 0.000 g45.2|1 (g45.) -0.017 0.038 -0.451 0.652 g47.2|1 (g47.) -0.352 0.044 -7.974 0.000 g51.2|1 (g51.) 1.071 0.056 19.269 0.000 g53.2|1 (g53.) 0.459 0.048 9.493 0.000 g55.2|1 (g55.) 0.071 0.038 1.863 0.062 g57.2|1 (g57.) 1.331 0.062 21.307 0.000 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.2 (t.1_) 1.193 0.405 2.948 0.003 .g4q3.2 (t.2_) 1.016 0.502 2.022 0.043 .g4q5.2 (t.3_) 1.461 0.998 1.463 0.143 .g4q7.2 (t.4_) 0.714 0.236 3.022 0.003 .g5q1.2 (t.5_) 1.355 0.202 6.711 0.000 .g5q3.2 (t.6_) 1.000 .g5q5.2 (t.7_) 2.939 2.883 1.020 0.308 .g5q7.2 (t.8_) 0.651 0.086 7.598 0.000 type2 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.2 0.869 g4q3.2 0.991 g4q5.2 0.720 g4q7.2 1.114 g5q1.2 0.843 g5q3.2 0.929 g5q5.2 0.574 g5q7.2 1.192 R-Square: Estimate g4q1.2 0.099 g4q3.2 0.002 g4q5.2 0.242 g4q7.2 0.113 g5q1.2 0.036 g5q3.2 0.137 g5q5.2 0.030 g5q7.2 0.075
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~``
> test_partial_th.lo_var.means<-measEq.syntax(type2, data=data, ID.cat="Wu.Estabrook.2016",group="group", group.equal=c("thresholds","loadings","intercepts","lv.variances","means"),warn=T, return.fit=T, group.partial=c("type2=~g5q3.2","g5q3.2|t1"),ordered=c("g4q1.2", "g4q3.2", "g4q5.2", "g4q7.2", "g5q1.2", "g5q3.2", "g5q5.2", "g5q7.2"),parameterization="theta", estimator="wlsmv", meanstructure=TRUE)
> summary(test_partial_th.lo_var.means, fit.measures=T, rsquare=T)
lavaan 0.6-3 ended normally after 133 iterations Optimization method NLMINB Number of free parameters 43Number of equality constraints 14
Number of observations per group 0 919 1 926 Estimator DWLS Robust Model Fit Test Statistic 46.194 48.741 Degrees of freedom 43 43 P-value (Chi-square) 0.342 0.253 Scaling correction factor 0.926 Shift parameter for each group: 0 -0.558 1 -0.563 for simple second-order correction (Mplus variant) Chi-square for each group: 0 27.350 28.963 1 18.844 19.778 Model test baseline model: Minimum Function Test Statistic 187.590 181.463 Degrees of freedom 56 56 P-value 0.000 0.000 User model versus baseline model: Comparative Fit Index (CFI) 0.976 0.954 Tucker-Lewis Index (TLI) 0.968 0.940 Robust Comparative Fit Index (CFI) NA Robust Tucker-Lewis Index (TLI) NA Root Mean Square Error of Approximation: RMSEA 0.009 0.012 90 Percent Confidence Interval 0.000 0.025 0.000 0.026 P-value RMSEA <= 0.05 1.000 1.000 Robust RMSEA NA 90 Percent Confidence Interval 0.000 NA Standardized Root Mean Square Residual: SRMR 0.055 0.055 Parameter Estimates: Information Expected Information saturated (h1) model Unstructured Standard Errors Robust.sem Group 1 [0]: Latent Variables: Estimate Std.Err z-value P(>|z|) type2 =~ g4q1.2 (l.1_) 0.361 0.076 4.754 0.000 g4q3.2 (l.2_) 0.043 0.055 0.782 0.434 g4q5.2 (l.3_) 0.683 0.178 3.831 0.000 g4q7.2 (l.4_) 0.302 0.065 4.660 0.000 g5q1.2 (l.5_) 0.226 0.076 2.954 0.003 g5q3.2 (l.6_) 0.122 0.075 1.618 0.106 g5q5.2 (l.7_) 0.304 0.088 3.463 0.001 g5q7.2 (l.8_) 0.230 0.082 2.815 0.005 Covariances: Estimate Std.Err z-value P(>|z|) .g4q3.2 ~~ .g5q5.2 (t.7_2) -0.152 0.055 -2.744 0.006 .g5q1.2 ~~ .g5q5.2 (t.7_5) -0.118 0.072 -1.652 0.099 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.2 (nu.1) 0.000 .g4q3.2 (nu.2) 0.000 .g4q5.2 (nu.3) 0.000 .g4q7.2 (nu.4) 0.000 .g5q1.2 (nu.5) 0.000 .g5q3.2 (nu.6) 0.000 .g5q5.2 (nu.7) 0.000 .g5q7.2 (nu.8) 0.000 type2 (al.1) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.2|1 (g41.) 0.389 0.046 8.440 0.000 g43.2|1 (g43.) -0.239 0.042 -5.725 0.000 g45.2|1 (g45.) -0.017 0.038 -0.451 0.652 g47.2|1 (g47.) -0.352 0.044 -7.974 0.000 g51.2|1 (g51.) 1.071 0.056 19.269 0.000 g53.2|1 (g53.) 0.481 0.044 11.027 0.000 g55.2|1 (g55.) 0.071 0.038 1.863 0.062 g57.2|1 (g57.) 1.331 0.062 21.307 0.000 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.2 (t.1_) 1.000 .g4q3.2 (t.2_) 1.000 .g4q5.2 (t.3_) 1.000 .g4q7.2 (t.4_) 1.000 .g5q1.2 (t.5_) 1.000 .g5q3.2 (t.6_) 1.000 .g5q5.2 (t.7_) 1.000 .g5q7.2 (t.8_) 1.000 type2 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.2 0.941 g4q3.2 0.999 g4q5.2 0.826 g4q7.2 0.957 g5q1.2 0.975 g5q3.2 0.993 g5q5.2 0.957 g5q7.2 0.975 R-Square: Estimate g4q1.2 0.115 g4q3.2 0.002 g4q5.2 0.318 g4q7.2 0.084 g5q1.2 0.048 g5q3.2 0.015 g5q5.2 0.084 g5q7.2 0.050 Group 2 [1]: Latent Variables: Estimate Std.Err z-value P(>|z|) type2 =~ g4q1.2 (l.1_) 0.361 0.076 4.754 0.000 g4q3.2 (l.2_) 0.043 0.055 0.782 0.434 g4q5.2 (l.3_) 0.683 0.178 3.831 0.000 g4q7.2 (l.4_) 0.302 0.065 4.660 0.000 g5q1.2 (l.5_) 0.226 0.076 2.954 0.003 g5q3.2 (l.6_) 0.398 0.101 3.940 0.000 g5q5.2 (l.7_) 0.304 0.088 3.463 0.001 g5q7.2 (l.8_) 0.230 0.082 2.815 0.005 Covariances: Estimate Std.Err z-value P(>|z|) .g4q3.2 ~~ .g5q5.2 (t.7_2) -0.282 0.177 -1.595 0.111 .g5q1.2 ~~ .g5q5.2 (t.7_5) -0.227 0.158 -1.441 0.150 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.2 (nu.1) 0.000 .g4q3.2 (nu.2) 0.000 .g4q5.2 (nu.3) 0.000 .g4q7.2 (nu.4) 0.000 .g5q1.2 (nu.5) 0.000 .g5q3.2 (nu.6) 0.000 .g5q5.2 (nu.7) 0.000 .g5q7.2 (nu.8) 0.000 type2 (al.1) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.2|1 (g41.) 0.389 0.046 8.440 0.000 g43.2|1 (g43.) -0.239 0.042 -5.725 0.000 g45.2|1 (g45.) -0.017 0.038 -0.451 0.652 g47.2|1 (g47.) -0.352 0.044 -7.974 0.000 g51.2|1 (g51.) 1.071 0.056 19.269 0.000 g53.2|1 (g53.) 0.459 0.048 9.493 0.000 g55.2|1 (g55.) 0.071 0.038 1.863 0.062 g57.2|1 (g57.) 1.331 0.062 21.307 0.000 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.2 (t.1_) 1.193 0.405 2.948 0.003 .g4q3.2 (t.2_) 1.016 0.502 2.022 0.043 .g4q5.2 (t.3_) 1.461 0.998 1.463 0.143 .g4q7.2 (t.4_) 0.714 0.236 3.022 0.003 .g5q1.2 (t.5_) 1.355 0.202 6.711 0.000 .g5q3.2 (t.6_) 1.000 .g5q5.2 (t.7_) 2.939 2.883 1.020 0.308 .g5q7.2 (t.8_) 0.651 0.086 7.598 0.000 type2 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.2 0.869 g4q3.2 0.991 g4q5.2 0.720 g4q7.2 1.114 g5q1.2 0.843 g5q3.2 0.929 g5q5.2 0.574 g5q7.2 1.192 R-Square: Estimate g4q1.2 0.099 g4q3.2 0.002 g4q5.2 0.242 g4q7.2 0.113 g5q1.2 0.036 g5q3.2 0.137 g5q5.2 0.030 g5q7.2 0.075
Terrence Jorgensen
For example, does adding "means" to group.equal= not lose a df because the means are already constrained in the model without "means" in group.equal=? Or because adding "means" to group.equal= does not give them the same labels to add the equality constraint, or because the means are not free parameters? This will help me figure out if I need to update the function.
cat(as.character(test_partial_th.lo.var))Pavneet Bharaj
Thanks Dr. Terrence.
Thanks for sharing the articles. Both are really meaningful. I have looked at the articles and the key-ideas that I have deducted from these:
1. Factor means, and variances are comparable when threshold, loading, and intercept invariance hold (Fischer’s article). In that article, they have tested the invariance of thresholds, loadings, intercepts, and residual variance.
2. From Wu’s article, one of the points that I found is that “to confirm that a model allows the comparison of factor means (or variances) one need to make sure that all possible identification conditions of this model do not involve such constraints, which is not discussed in this paper” (p.1033).
Based on Wu’s advice, I went back to my previous models to see the structure of the model when “threshold, loading, intercepts” are fixed, and I found that the mean of both the groups are fixed to 0, even though it is not specified by when I checked the fixed parameters of the model using fit.measure=F (I am attaching the output and code underneath).
I also checked the documentation of measEq.syntax function which specified that the ID.fac can be used “for identifying common-factor variances and (if meanstructure = TRUE) means”.
Even though I have used ID.fac=”std.lv” and used meanstructure=T, yet the mean is zero for both of groups (not only the reference group. Wu mentioned that factor variance and means for reference group is set to 1 and o resp. But I am getting means zero for both groups)
Now, I am wondering, is mean automatically fixed to 0 for both groups (my assumption due to binary data) and that is why I am unable to compare means using group.equal?
I really want to study the comparison of means of both groups, but in case if that is already fixed to zero for identification purposes, I need to inform the readers of my paper about it.
Please correct me if I am thinking wrong.
Regards,
Pavneet Kaur
test_partial_th.lo<-measEq.syntax(type2, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal=c("thresholds","loadings"),
group.partial=c("type2=~g5q3.2","g5q3.2|t1"),warn=T, return.fit=T,
ordered=c("g4q1.2", "g4q3.2", "g4q5.2", "g4q7.2",
"g5q1.2", "g5q3.2", "g5q5.2", "g5q7.2"),
parameterization="theta", estimator="wlsmv",
meanstructure=TRUE, ID.fac="std.lv")
summary(test_partial_th.lo, fit.measures=T, rsquare=T)
> summary(test_partial_th.lo, fit.measures=T, rsquare=T)
lavaan 0.6-3 ended normally after 66 iterations
Optimization method NLMINB
Number of free parameters 44
Number of equality constraints 14
Number of observations per group
0 919
1 926
Estimator DWLS Robust
Model Fit Test Statistic 44.545 46.997
Degrees of freedom 42 42
P-value (Chi-square) 0.365 0.275
Scaling correction factor 0.933
Shift parameter for each group:
0 -0.370
1 -0.373
for simple second-order correction (Mplus variant)
Chi-square for each group:
0 26.195 27.704
1 18.350 19.293
Model test baseline model:
Minimum Function Test Statistic 187.590 181.463
Degrees of freedom 56 56
P-value 0.000 0.000
User model versus baseline model:
Comparative Fit Index (CFI) 0.981 0.960
Tucker-Lewis Index (TLI) 0.974 0.947
Robust Comparative Fit Index (CFI) NA
Robust Tucker-Lewis Index (TLI) NA
Root Mean Square Error of Approximation:
RMSEA 0.008 0.011
90 Percent Confidence Interval 0.000 0.024 0.000 0.026
P-value RMSEA <= 0.05 1.000 1.000
Robust RMSEA NA
90 Percent Confidence Interval 0.000 NA
Standardized Root Mean Square Residual:
SRMR 0.053 0.053
Parameter Estimates:
Information Expected
Information saturated (h1) model Unstructured
Standard Errors Robust.sem
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type2 =~
g4q1.2 (l.1_) 0.378 0.075 5.052 0.000
g4q3.2 (l.2_) 0.051 0.057 0.890 0.374
g4q5.2 (l.3_) 0.639 0.118 5.406 0.000
g4q7.2 (l.4_) 0.352 0.073 4.850 0.000
g5q1.2 (l.5_) 0.229 0.075 3.060 0.002
g5q3.2 (l.6_) 0.119 0.076 1.574 0.116
g5q5.2 (l.7_) 0.250 0.063 3.938 0.000
g5q7.2 (l.8_) 0.290 0.094 3.095 0.002
Covariances:
Estimate Std.Err z-value P(>|z|)
.g4q3.2 ~~
.g5q5.2 (t.7_2) -0.150 0.054 -2.766 0.006
.g5q1.2 ~~
.g5q5.2 (t.7_5) -0.106 0.069 -1.543 0.123
Intercepts:
Estimate Std.Err z-value P(>|z|)
.g4q1.2 (n.1.) 0.000
.g4q3.2 (n.2.) 0.000
.g4q5.2 (n.3.) 0.000
.g4q7.2 (n.4.) 0.000
.g5q1.2 (n.5.) 0.000
.g5q3.2 (n.6.) 0.000
.g5q5.2 (n.7.) 0.000
.g5q7.2 (n.8.) 0.000
type2 (a.1.) 0.000
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.2|1 (g41.) 0.405 0.046 8.732 0.000
g43.2|1 (g43.) -0.236 0.042 -5.632 0.000
g45.2|1 (g45.) -0.021 0.049 -0.428 0.668
g47.2|1 (g47.) -0.352 0.045 -7.752 0.000
g51.2|1 (g51.) 1.077 0.055 19.682 0.000
g53.2|1 (g53.) 0.480 0.044 11.028 0.000
g55.2|1 (g55.) 0.069 0.043 1.615 0.106
g57.2|1 (g57.) 1.340 0.067 20.149 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.g4q1.2 (t.1_) 1.000
.g4q3.2 (t.2_) 1.000
.g4q5.2 (t.3_) 1.000
.g4q7.2 (t.4_) 1.000
.g5q1.2 (t.5_) 1.000
.g5q3.2 (t.6_) 1.000
.g5q5.2 (t.7_) 1.000
.g5q7.2 (t.8_) 1.000
type2 (p.1_) 1.000
Scales y*:
Estimate Std.Err z-value P(>|z|)
g4q1.2 0.935
g4q3.2 0.999
g4q5.2 0.843
g4q7.2 0.943
g5q1.2 0.975
g5q3.2 0.993
g5q5.2 0.970
g5q7.2 0.960
R-Square:
Estimate
g4q1.2 0.125
g4q3.2 0.003
g4q5.2 0.290
g4q7.2 0.110
g5q1.2 0.050
g5q3.2 0.014
g5q5.2 0.059
g5q7.2 0.078
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type2 =~
g4q1.2 (l.1_) 0.378 0.075 5.052 0.000
g4q3.2 (l.2_) 0.051 0.057 0.890 0.374
g4q5.2 (l.3_) 0.639 0.118 5.406 0.000
g4q7.2 (l.4_) 0.352 0.073 4.850 0.000
g5q1.2 (l.5_) 0.229 0.075 3.060 0.002
g5q3.2 (l.6_) 0.442 0.136 3.244 0.001
g5q5.2 (l.7_) 0.250 0.063 3.938 0.000
g5q7.2 (l.8_) 0.290 0.094 3.095 0.002
Covariances:
Estimate Std.Err z-value P(>|z|)
.g4q3.2 ~~
.g5q5.2 (t.7_2) -0.167 0.054 -3.121 0.002
.g5q1.2 ~~
.g5q5.2 (t.7_5) -0.126 0.064 -1.966 0.049
Intercepts:
Estimate Std.Err z-value P(>|z|)
.g4q1.2 (n.1.) 0.062 0.064 0.966 0.334
.g4q3.2 (n.2.) 0.005 0.059 0.086 0.931
.g4q5.2 (n.3.) -0.012 0.068 -0.171 0.864
.g4q7.2 (n.4.) 0.065 0.063 1.020 0.308
.g5q1.2 (n.5.) 0.161 0.072 2.240 0.025
.g5q3.2 (n.6.) 0.000
.g5q5.2 (n.7.) 0.025 0.060 0.409 0.683
.g5q7.2 (n.8.) -0.310 0.092 -3.374 0.001
type2 (a.1.) 0.000
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.2|1 (g41.) 0.405 0.046 8.732 0.000
g43.2|1 (g43.) -0.236 0.042 -5.632 0.000
g45.2|1 (g45.) -0.021 0.049 -0.428 0.668
g47.2|1 (g47.) -0.352 0.045 -7.752 0.000
g51.2|1 (g51.) 1.077 0.055 19.682 0.000
g53.2|1 (g53.) 0.459 0.048 9.504 0.000
g55.2|1 (g55.) 0.069 0.043 1.615 0.106
g57.2|1 (g57.) 1.340 0.067 20.149 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.g4q1.2 (t.1_) 1.000
.g4q3.2 (t.2_) 1.000
.g4q5.2 (t.3_) 1.000
.g4q7.2 (t.4_) 1.000
.g5q1.2 (t.5_) 1.000
.g5q3.2 (t.6_) 1.000
.g5q5.2 (t.7_) 1.000
.g5q7.2 (t.8_) 1.000
type2 (p.1_) 0.795 0.223 3.564 0.000
Scales y*:
Estimate Std.Err z-value P(>|z|)
g4q1.2 0.948
g4q3.2 0.999
g4q5.2 0.869
g4q7.2 0.954
g5q1.2 0.980
g5q3.2 0.930
g5q5.2 0.976
g5q7.2 0.968
R-Square:
Estimate
g4q1.2 0.102
g4q3.2 0.002
g4q5.2 0.245
g4q7.2 0.090
g5q1.2 0.040
g5q3.2 0.134
g5q5.2 0.047
g5q7.2 0.063
Terrence Jorgensen
1. Factor means, and variances are comparable when threshold, loading, and intercept invariance hold (Fischer’s article). In that article, they have tested the invariance of thresholds, loadings, intercepts, and residual variance.
I went back to my previous models to see the structure of the model when “threshold, loading, intercepts” are fixed, and I found that the mean of both the groups are fixed to 0,
myData <- read.table("http://www.statmodel.com/usersguide/chap5/ex5.16.dat")
names(myData) <- c("u1","u2","u3","u4","u5","u6","x1","x2","x3","g")
## fit initial model
library(lavaan)
bin.mod <- '
FU1 =~ u1 + u2 + u3
FU2 =~ u4 + u5 + u6
'
bin.fit <- cfa(bin.mod, data = myData, ordered = paste0("u", 1:6),
std.lv = TRUE, group = "g", parameterization = "theta")
## save syntax objects (options from fitted model are retained)
library(semTools)
mod.config <- measEq.syntax(configural.model = bin.fit, group = "g")
mod.thresh <- measEq.syntax(configural.model = bin.fit,group = "g",
group.equal = c("thresholds"))
mod.metric <- measEq.syntax(configural.model = bin.fit, group = "g",
group.equal = c("thresholds","loadings"))
mod.scalar <- measEq.syntax(configural.model = bin.fit, group = "g",
group.equal = c("thresholds","loadings","intercepts"))## all common-factor means = 0, all latent item-response intercepts = 0
## all common-factor variances = 1, all latent item-response residual variances = 1
cat(as.character(mod.config))
## all common-factor means = 0, latent item-response intercepts = 0 only in first group
## all common-factor variances = 1, all latent item-response residual variances = 1
cat(as.character(mod.thresh))
## all common-factor means = 0, latent item-response intercepts = 0 only in first group
## common-factor variances = 1 only in first group, all latent item-response residual variances = 1
cat(as.character(mod.metric))
## common-factor means = 0 only in first group, all latent item-response intercepts = 0
## common-factor variances = 1 only in first group,
## latent item-response residual variances = 1 only in first group
cat(as.character(mod.scalar))sessionInfo()even though it is not specified by when I checked the fixed parameters of the model using fit.measure=F
Pavneet Bharaj
Good Morning Dr. Terrence,
Thanks a lot for your reply.
And I checked I have semTools version 0.5-1.907 installed.
And previous email, I meant return.fit=F (instead of fit.measure=F). Sorry for that.
The model you just shared to compare with cat(as.character()) was really useful as I think it helped in figure out a point where my model is behaving differently than the one you just shared with me.
So, for the argument group.equal=c("thresholds", "loadings", "intercepts"), there is a difference between the output of the models for the model that you shared and for my model. I am attaching the code and output here (with some highlights). I feel that free estimated value as c(0, NA) in your model helps in extracting the means difference between groups when we want to compare the means in group.equal= argument.
Please let me know if I am committing any error in the specification of model.
I really appreciate your help.
Regards,
Pavneet Kaur
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
type5 <- 't5=~ g4q1.5+ g4q3.5+ g4q5.5 + g4q7.5 + g5q1.5+ g5q3.5+ g5q5.5 + g5q7.5
g5q1.5 ~~ g5q5.5'
fit.type5<- cfa(model=type5, data=data, group="group", parameterization="theta", estimator="wlsmv", meanstructure=T, std.lv=T, ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5", "g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"))
summary(fit.type5, standardized=T , rsquare=T, fit.measures=T)
#---- using measEqsynatx( ) --------#
mod.configural<-measEq.syntax(fit.type5, group="group")
mod.scalar<-measEq.syntax(fit.type5, group.equal=c("thresholds","loadings","intercepts"))
cat(as.character(mod.configural))
cat(as.character(mod.scalar))
RESULTS FROM cat(as.character(mod.configural))
> cat(as.character(mod.configural))
## LOADINGS:
t5 =~ c(NA, NA)*g4q1.5 + c(lambda.1_1.g1, lambda.1_1.g2)*g4q1.5
t5 =~ c(NA, NA)*g4q3.5 + c(lambda.2_1.g1, lambda.2_1.g2)*g4q3.5
t5 =~ c(NA, NA)*g4q5.5 + c(lambda.3_1.g1, lambda.3_1.g2)*g4q5.5
t5 =~ c(NA, NA)*g4q7.5 + c(lambda.4_1.g1, lambda.4_1.g2)*g4q7.5
t5 =~ c(NA, NA)*g5q1.5 + c(lambda.5_1.g1, lambda.5_1.g2)*g5q1.5
t5 =~ c(NA, NA)*g5q3.5 + c(lambda.6_1.g1, lambda.6_1.g2)*g5q3.5
t5 =~ c(NA, NA)*g5q5.5 + c(lambda.7_1.g1, lambda.7_1.g2)*g5q5.5
t5 =~ c(NA, NA)*g5q7.5 + c(lambda.8_1.g1, lambda.8_1.g2)*g5q7.5
## THRESHOLDS:
g4q1.5 | c(NA, NA)*t1 + c(g4q1.5.thr1.g1, g4q1.5.thr1.g2)*t1
g4q3.5 | c(NA, NA)*t1 + c(g4q3.5.thr1.g1, g4q3.5.thr1.g2)*t1
g4q5.5 | c(NA, NA)*t1 + c(g4q5.5.thr1.g1, g4q5.5.thr1.g2)*t1
g4q7.5 | c(NA, NA)*t1 + c(g4q7.5.thr1.g1, g4q7.5.thr1.g2)*t1
g5q1.5 | c(NA, NA)*t1 + c(g5q1.5.thr1.g1, g5q1.5.thr1.g2)*t1
g5q3.5 | c(NA, NA)*t1 + c(g5q3.5.thr1.g1, g5q3.5.thr1.g2)*t1
g5q5.5 | c(NA, NA)*t1 + c(g5q5.5.thr1.g1, g5q5.5.thr1.g2)*t1
g5q7.5 | c(NA, NA)*t1 + c(g5q7.5.thr1.g1, g5q7.5.thr1.g2)*t1
## INTERCEPTS:
g4q1.5 ~ c(nu.1.g1, nu.1.g2)*1 + c(0, 0)*1
g4q3.5 ~ c(nu.2.g1, nu.2.g2)*1 + c(0, 0)*1
g4q5.5 ~ c(nu.3.g1, nu.3.g2)*1 + c(0, 0)*1
g4q7.5 ~ c(nu.4.g1, nu.4.g2)*1 + c(0, 0)*1
g5q1.5 ~ c(nu.5.g1, nu.5.g2)*1 + c(0, 0)*1
g5q3.5 ~ c(nu.6.g1, nu.6.g2)*1 + c(0, 0)*1
g5q5.5 ~ c(nu.7.g1, nu.7.g2)*1 + c(0, 0)*1
g5q7.5 ~ c(nu.8.g1, nu.8.g2)*1 + c(0, 0)*1
## UNIQUE-FACTOR VARIANCES:
g4q1.5 ~~ c(1, 1)*g4q1.5 + c(theta.1_1.g1, theta.1_1.g2)*g4q1.5
g4q3.5 ~~ c(1, 1)*g4q3.5 + c(theta.2_2.g1, theta.2_2.g2)*g4q3.5
g4q5.5 ~~ c(1, 1)*g4q5.5 + c(theta.3_3.g1, theta.3_3.g2)*g4q5.5
g4q7.5 ~~ c(1, 1)*g4q7.5 + c(theta.4_4.g1, theta.4_4.g2)*g4q7.5
g5q1.5 ~~ c(1, 1)*g5q1.5 + c(theta.5_5.g1, theta.5_5.g2)*g5q1.5
g5q3.5 ~~ c(1, 1)*g5q3.5 + c(theta.6_6.g1, theta.6_6.g2)*g5q3.5
g5q5.5 ~~ c(1, 1)*g5q5.5 + c(theta.7_7.g1, theta.7_7.g2)*g5q5.5
g5q7.5 ~~ c(1, 1)*g5q7.5 + c(theta.8_8.g1, theta.8_8.g2)*g5q7.5
## UNIQUE-FACTOR COVARIANCES:
g5q1.5 ~~ c(NA, NA)*g5q5.5 + c(theta.7_5.g1, theta.7_5.g2)*g5q5.5
## LATENT MEANS/INTERCEPTS:
t5 ~ c(alpha.1.g1, alpha.1.g2)*1 + c(0, 0)*1
## COMMON-FACTOR VARIANCES:
t5 ~~ c(1, 1)*t5 + c(psi.1_1.g1, psi.1_1.g2)*t5
THE MODEL YOU SHARED HAS YIELDED for configural:
## LATENT MEANS/INTERCEPTS:
FU1 ~ c(alpha.1.g1, alpha.1.g2)*1 + c(0, 0)*1
FU2 ~ c(alpha.2.g1, alpha.2.g2)*1 + c(0, 0)*1
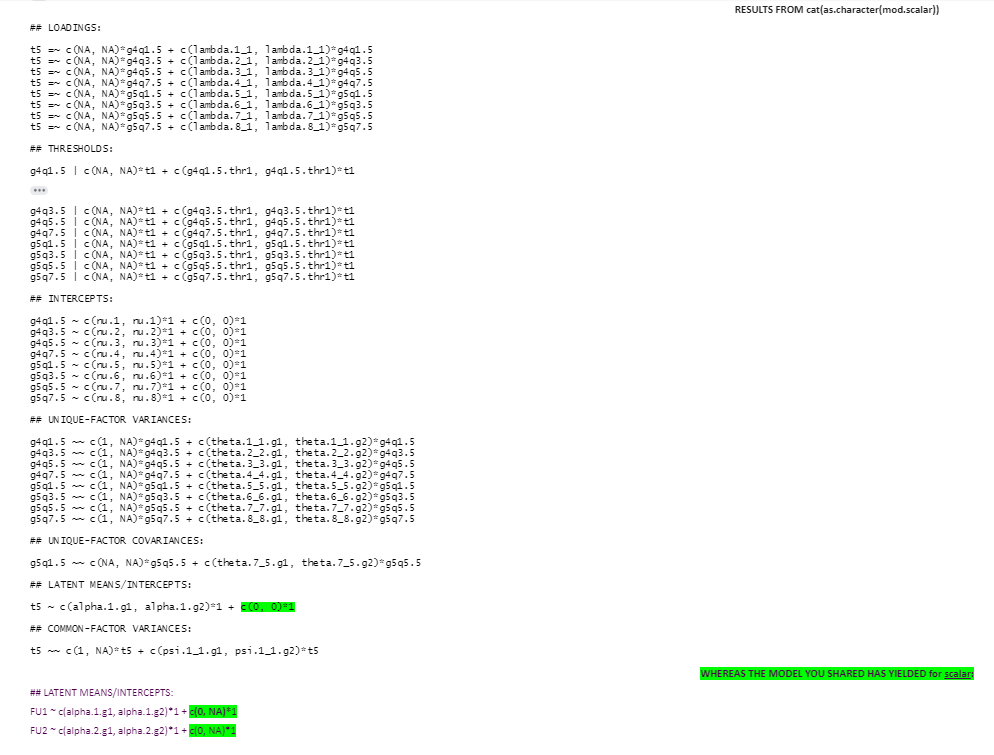
RESULTS FROM cat(as.character(mod.scalar))
## LOADINGS: t5 =~ c(NA, NA)*g4q1.5 + c(lambda.1_1, lambda.1_1)*g4q1.5t5 =~ c(NA, NA)*g4q3.5 + c(lambda.2_1, lambda.2_1)*g4q3.5t5 =~ c(NA, NA)*g4q5.5 + c(lambda.3_1, lambda.3_1)*g4q5.5t5 =~ c(NA, NA)*g4q7.5 + c(lambda.4_1, lambda.4_1)*g4q7.5t5 =~ c(NA, NA)*g5q1.5 + c(lambda.5_1, lambda.5_1)*g5q1.5t5 =~ c(NA, NA)*g5q3.5 + c(lambda.6_1, lambda.6_1)*g5q3.5t5 =~ c(NA, NA)*g5q5.5 + c(lambda.7_1, lambda.7_1)*g5q5.5t5 =~ c(NA, NA)*g5q7.5 + c(lambda.8_1, lambda.8_1)*g5q7.5 ## THRESHOLDS: g4q1.5 | c(NA, NA)*t1 + c(g4q1.5.thr1, g4q1.5.thr1)*t1g4q3.5 | c(NA, NA)*t1 + c(g4q3.5.thr1, g4q3.5.thr1)*t1g4q5.5 | c(NA, NA)*t1 + c(g4q5.5.thr1, g4q5.5.thr1)*t1g4q7.5 | c(NA, NA)*t1 + c(g4q7.5.thr1, g4q7.5.thr1)*t1g5q1.5 | c(NA, NA)*t1 + c(g5q1.5.thr1, g5q1.5.thr1)*t1g5q3.5 | c(NA, NA)*t1 + c(g5q3.5.thr1, g5q3.5.thr1)*t1g5q5.5 | c(NA, NA)*t1 + c(g5q5.5.thr1, g5q5.5.thr1)*t1g5q7.5 | c(NA, NA)*t1 + c(g5q7.5.thr1, g5q7.5.thr1)*t1 ## INTERCEPTS: g4q1.5 ~ c(nu.1, nu.1)*1 + c(0, 0)*1g4q3.5 ~ c(nu.2, nu.2)*1 + c(0, 0)*1g4q5.5 ~ c(nu.3, nu.3)*1 + c(0, 0)*1g4q7.5 ~ c(nu.4, nu.4)*1 + c(0, 0)*1g5q1.5 ~ c(nu.5, nu.5)*1 + c(0, 0)*1g5q3.5 ~ c(nu.6, nu.6)*1 + c(0, 0)*1g5q5.5 ~ c(nu.7, nu.7)*1 + c(0, 0)*1g5q7.5 ~ c(nu.8, nu.8)*1 + c(0, 0)*1 ## UNIQUE-FACTOR VARIANCES: g4q1.5 ~~ c(1, NA)*g4q1.5 + c(theta.1_1.g1, theta.1_1.g2)*g4q1.5g4q3.5 ~~ c(1, NA)*g4q3.5 + c(theta.2_2.g1, theta.2_2.g2)*g4q3.5g4q5.5 ~~ c(1, NA)*g4q5.5 + c(theta.3_3.g1, theta.3_3.g2)*g4q5.5g4q7.5 ~~ c(1, NA)*g4q7.5 + c(theta.4_4.g1, theta.4_4.g2)*g4q7.5g5q1.5 ~~ c(1, NA)*g5q1.5 + c(theta.5_5.g1, theta.5_5.g2)*g5q1.5g5q3.5 ~~ c(1, NA)*g5q3.5 + c(theta.6_6.g1, theta.6_6.g2)*g5q3.5g5q5.5 ~~ c(1, NA)*g5q5.5 + c(theta.7_7.g1, theta.7_7.g2)*g5q5.5g5q7.5 ~~ c(1, NA)*g5q7.5 + c(theta.8_8.g1, theta.8_8.g2)*g5q7.5 ## UNIQUE-FACTOR COVARIANCES: g5q1.5 ~~ c(NA, NA)*g5q5.5 + c(theta.7_5.g1, theta.7_5.g2)*g5q5.5 ## LATENT MEANS/INTERCEPTS: t5 ~ c(alpha.1.g1, alpha.1.g2)*1 + c(0, 0)*1 ## COMMON-FACTOR VARIANCES: t5 ~~ c(1, NA)*t5 + c(psi.1_1.g1, psi.1_1.g2)*t5
WHEREAS THE MODEL YOU SHARED HAS YIELDED for scalar:
## LATENT MEANS/INTERCEPTS:
FU1 ~ c(alpha.1.g1, alpha.1.g2)*1 + c(0, NA)*1
FU2 ~ c(alpha.2.g1, alpha.2.g2)*1 + c(0, NA)*1
Terrence Jorgensen
RESULTS FROM cat(as.character(mod.scalar))
## LOADINGS:t5 =~ c(NA, NA)*g4q1.5 + c(lambda.1_1, lambda.1_1)*g4q1.5t5 =~ c(NA, NA)*g4q3.5 + c(lambda.2_1, lambda.2_1)*g4q3.5t5 =~ c(NA, NA)*g4q5.5 + c(lambda.3_1, lambda.3_1)*g4q5.5t5 =~ c(NA, NA)*g4q7.5 + c(lambda.4_1, lambda.4_1)*g4q7.5t5 =~ c(NA, NA)*g5q1.5 + c(lambda.5_1, lambda.5_1)*g5q1.5t5 =~ c(NA, NA)*g5q3.5 + c(lambda.6_1, lambda.6_1)*g5q3.5t5 =~ c(NA, NA)*g5q5.5 + c(lambda.7_1, lambda.7_1)*g5q5.5t5 =~ c(NA, NA)*g5q7.5 + c(lambda.8_1, lambda.8_1)*g5q7.5## THRESHOLDS:
<span style="font-family:"Lucida Console";color:black;border:1pt none windowte
Pavneet Bharaj
Good Evening Dr. Terrence.
I hope this works. I am pasting the syntax as well as the output. I highlighted the o output in green to show the difference in results between the model that you stated above and the model that I have specified.
type5 <- 't5=~ g4q1.5+ g4q3.5+ g4q5.5 + g4q7.5 + g5q1.5+ g5q3.5+ g5q5.5 + g5q7.5
g5q1.5 ~~ g5q5.5'
fit.type5<- cfa(model=type5, data=data, group="group", parameterization="theta", estimator="wlsmv", meanstructure=T, std.lv=T, ordered=c("g4q1.5", "g4q3.5", "g4q5.5", "g4q7.5", "g5q1.5", "g5q3.5", "g5q5.5", "g5q7.5"))
summary(fit.type5, standardized=T , rsquare=T, fit.measures=T)
#---- using measEqsynatx( ) --------#
mod.configural<-measEq.syntax(fit.type5, group="group")
mod.scalar<-measEq.syntax(fit.type5, group.equal=c("thresholds","loadings","intercepts"))
cat(as.character(mod.configural))
cat(as.character(mod.scalar))
RESULTS FROM cat(as.character(mod.configural))
> cat(as.character(mod.configural))
## LOADINGS:
t5 =~ c(NA, NA)*g4q1.5 + c(lambda.1_1.g1, lambda.1_1.g2)*g4q1.5
RESULTS FROM cat(as.character(mod.scalar))
## LOADINGS: t5 =~ c(NA, NA)*g4q1.5 + c(lambda.1_1, lambda.1_1)*g4q1.5t5 =~ c(NA, NA)*g4q3.5 + c(lambda.2_1, lambda.2_1)*g4q3.5t5 =~ c(NA, NA)*g4q5.5 + c(lambda.3_1, lambda.3_1)*g4q5.5t5 =~ c(NA, NA)*g4q7.5 + c(lambda.4_1, lambda.4_1)*g4q7.5t5 =~ c(NA, NA)*g5q1.5 + c(lambda.5_1, lambda.5_1)*g5q1.5t5 =~ c(NA, NA)*g5q3.5 + c(lambda.6_1, lambda.6_1)*g5q3.5t5 =~ c(NA, NA)*g5q5.5 + c(lambda.7_1, lambda.7_1)*g5q5.5t5 =~ c(NA, NA)*g5q7.5 + c(lambda.8_1, lambda.8_1)*g5q7.5 ## THRESHOLDS: g4q1.5 | c(NA, NA)*t1 + c(g4q1.5.thr1, g4q1.5.thr1)*t1Pavneet Bharaj
Terrence Jorgensen
I am also attaching a screenshot of the output of "scalar" model.
devtools::install_github("simsem/semTools/semTools")Pavneet Bharaj
Pavneet Bharaj
Good Evening Dr. Terrence.
I am working on checking the partial invariance of the model:
type4 <- 'type4=~ g4q1.4+ g4q3.4+ g4q5.4 + g4q7.4 + g5q1.4+ g5q3.4+ g5q5.4 + g5q7.4
g5q1.4 ~~ g5q7.4'
So, in this model I tried to assess for which item I need to freely estimate the factor loadings to attain the invariance at loadings, threshold, and intercepts level (Since my data is binary).
For some of the items, when I freely estimated the loadings for both groups, I got results as:
test_partial_1<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal=c("thresholds","loadings","intercepts"), group.partial=c("type4=~g4q1.4"),warn=T, return.fit=T, parameterization="theta", estimator="wlsmv", meanstructure=TRUE,std.lv=T, ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"))
> summary(test_partial_1, fit.measures=T, rsquare=T)
lavaan 0.6-3 ended normally after 176 iterations
Optimization method NLMINB
Number of free parameters 44
Number of equality constraints 15
Number of observations per group
0 919
1 926
Estimator DWLS Robust
Model Fit Test Statistic 58.451 64.028
Degrees of freedom 43 43
P-value (Chi-square) 0.058 0.020
Scaling correction factor 0.911
Shift parameter for each group:
0 -0.063
1 -0.064
for simple second-order correction (Mplus variant)
Chi-square for each group:
0 29.154 31.936
1 29.297 32.092
Model test baseline model:
Minimum Function Test Statistic 312.409 302.732
Degrees of freedom 56 56
P-value 0.000 0.000
User model versus baseline model:
Comparative Fit Index (CFI) 0.940 0.915
Tucker-Lewis Index (TLI) 0.922 0.889
Robust Comparative Fit Index (CFI) NA
Robust Tucker-Lewis Index (TLI) NA
Root Mean Square Error of Approximation:
RMSEA 0.020 0.023
90 Percent Confidence Interval 0.000 0.032 0.009 0.034
P-value RMSEA <= 0.05 1.000 1.000
Robust RMSEA NA
90 Percent Confidence Interval NA NA
Standardized Root Mean Square Residual:
SRMR 0.043 0.043
Parameter Estimates:
Information Expected
Information saturated (h1) model Unstructured
Standard Errors Robust.sem
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type4 =~
g4q1.4 (l.1_) 0.152 0.069 2.212 0.027
g4q3.4 (l.2_) 0.362 0.072 5.029 0.000
g4q5.4 (l.3_) 0.519 0.099 5.269 0.000
g4q7.4 (l.4_) 0.435 0.079 5.529 0.000
g5q1.4 (l.5_) 0.601 0.109 5.528 0.000
g5q3.4 (l.6_) 0.345 0.079 4.363 0.000
g5q5.4 (l.7_) 0.294 0.074 3.974 0.000
g5q7.4 (l.8_) -0.024 0.024 -1.014 0.311
Covariances:
Estimate Std.Err z-value P(>|z|)
.g5q1.4 ~~
.g5q7.4 (t.8_) -0.248 0.061 -4.070 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
.g4q1.4 (nu.1) 0.000
.g4q3.4 (nu.2) 0.000
.g4q5.4 (nu.3) 0.000
.g4q7.4 (nu.4) 0.000
.g5q1.4 (nu.5) 0.000
.g5q3.4 (nu.6) 0.000
.g5q5.4 (nu.7) 0.000
.g5q7.4 (nu.8) 0.000
type4 (a.1.) 0.000
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.4|1 (g41.) -0.413 0.043 -9.537 0.000
g43.4|1 (g43.) -0.979 0.056 -17.524 0.000
g45.4|1 (g45.) 0.015 0.046 0.322 0.747
g47.4|1 (g47.) -0.562 0.050 -11.291 0.000
g51.4|1 (g51.) -0.248 0.049 -5.072 0.000
g53.4|1 (g53.) 0.130 0.043 3.049 0.002
g55.4|1 (g55.) -0.105 0.041 -2.559 0.011
g57.4|1 (g57.) 0.379 0.042 8.917 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.g4q1.4 (t.1_) 1.000
.g4q3.4 (t.2_) 1.000
.g4q5.4 (t.3_) 1.000
.g4q7.4 (t.4_) 1.000
.g5q1.4 (t.5_) 1.000
.g5q3.4 (t.6_) 1.000
.g5q5.4 (t.7_) 1.000
.g5q7.4 (t.8_) 1.000
type4 (p.1_) 1.000
Scales y*:
Estimate Std.Err z-value P(>|z|)
g4q1.4 0.989
g4q3.4 0.940
g4q5.4 0.888
g4q7.4 0.917
g5q1.4 0.857
g5q3.4 0.945
g5q5.4 0.959
g5q7.4 1.000
R-Square:
Estimate
g4q1.4 0.023
g4q3.4 0.116
g4q5.4 0.212
g4q7.4 0.159
g5q1.4 0.266
g5q3.4 0.106
g5q5.4 0.080
g5q7.4 0.001
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type4 =~
g4q1.4 (l.1_) 0.059 0.063 0.941 0.347
g4q3.4 (l.2_) 0.362 0.072 5.029 0.000
g4q5.4 (l.3_) 0.519 0.099 5.269 0.000
g4q7.4 (l.4_) 0.435 0.079 5.529 0.000
g5q1.4 (l.5_) 0.601 0.109 5.528 0.000
g5q3.4 (l.6_) 0.345 0.079 4.363 0.000
g5q5.4 (l.7_) 0.294 0.074 3.974 0.000
g5q7.4 (l.8_) -0.024 0.024 -1.014 0.311
Covariances:
Estimate Std.Err z-value P(>|z|)
.g5q1.4 ~~
.g5q7.4 (t.8_) -0.197 0.112 -1.764 0.078
Intercepts:
Estimate Std.Err z-value P(>|z|)
.g4q1.4 (nu.1) 0.000
.g4q3.4 (nu.2) 0.000
.g4q5.4 (nu.3) 0.000
.g4q7.4 (nu.4) 0.000
.g5q1.4 (nu.5) 0.000
.g5q3.4 (nu.6) 0.000
.g5q5.4 (nu.7) 0.000
.g5q7.4 (nu.8) 0.000
type4 (a.1.) 0.473 0.242 1.960 0.050
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.4|1 (g41.) -0.413 0.043 -9.537 0.000
g43.4|1 (g43.) -0.979 0.056 -17.524 0.000
g45.4|1 (g45.) 0.015 0.046 0.322 0.747
g47.4|1 (g47.) -0.562 0.050 -11.291 0.000
g51.4|1 (g51.) -0.248 0.049 -5.072 0.000
g53.4|1 (g53.) 0.130 0.043 3.049 0.002
g55.4|1 (g55.) -0.105 0.041 -2.559 0.011
g57.4|1 (g57.) 0.379 0.042 8.917 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.g4q1.4 (t.1_) 2.324 0.921 2.523 0.012
.g4q3.4 (t.2_) 1.158 0.236 4.902 0.000
.g4q5.4 (t.3_) 18.140 15.517 1.169 0.242
.g4q7.4 (t.4_) 1.612 0.580 2.781 0.005
.g5q1.4 (t.5_) 6.015 3.908 1.539 0.124
.g5q3.4 (t.6_) 4.381 3.515 1.246 0.213
.g5q5.4 (t.7_) 4.253 3.381 1.258 0.209
.g5q7.4 (t.8_) 0.320 0.085 3.761 0.000
type4 (p.1_) 3.402 1.379 2.467 0.014
Scales y*:
Estimate Std.Err z-value P(>|z|)
g4q1.4 0.654
g4q3.4 0.790
g4q5.4 0.229
g4q7.4 0.666
g5q1.4 0.372
g5q3.4 0.457
g5q5.4 0.469
g5q7.4 1.762
R-Square:
Estimate
g4q1.4 0.005
g4q3.4 0.278
g4q5.4 0.048
g4q7.4 0.285
g5q1.4 0.170
g5q3.4 0.085
g5q5.4 0.065
g5q7.4 0.006
But, when I tried to use the same code for some other items (within above model), I got this message:
test_partial_3<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal=c("thresholds","loadings","intercepts"), parameterization="theta", estimator="wlsmv",meanstructure=TRUE, std.lv=T, group.partial=c("type4=~g4q5.4"),warn=T, return.fit=T, ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"))
Warning messages:1: In lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats, : lavaan WARNING: The variance-covariance matrix of the estimated parameters (vcov) does not appear to be positive definite! The smallest eigenvalue (= 2.197847e-14) is close to zero. This may be a symptom that the model is not identified.2: In lavaan::lavaan(model = "## LOADINGS:\n\ntype4 =~ c(NA, NA)*g4q1.4 + c(lambda.1_1, lambda.1_1)*g4q1.4\ntype4 =~ c(NA, NA)*g4q3.4 + c(lambda.2_1, lambda.2_1)*g4q3.4\ntype4 =~ c(NA, NA)*g4q5.4 + c(lambda.3_1.g1, lambda.3_1.g2)*g4q5.4\ntype4 =~ c(NA, NA)*g4q7.4 + c(lambda.4_1, lambda.4_1)*g4q7.4\ntype4 =~ c(NA, NA)*g5q1.4 + c(lambda.5_1, lambda.5_1)*g5q1.4\ntype4 =~ c(NA, NA)*g5q3.4 + c(lambda.6_1, lambda.6_1)*g5q3.4\ntype4 =~ c(NA, NA)*g5q5.4 + c(lambda.7_1, lambda.7_1)*g5q5.4\ntype4 =~ c(NA, NA)*g5q7.4 + c(lambda.8_1, lambda.8_1)*g5q7.4\n\n## THRESHOLDS:\n\ng4q1.4 | c(NA, NA)*t1 + c(g4q1.4.thr1, g4q1.4.thr1)*t1\ng4q3.4 | c(NA, NA)*t1 + c(g4q3.4.thr1, g4q3.4.thr1)*t1\ng4q5.4 | c(NA, NA)*t1 + c(g4q5.4.thr1, g4q5.4.thr1)*t1\ng4q7.4 | c(NA, NA)*t1 + c(g4q7.4.thr1, g4q7.4.thr1)*t1\ng5q1.4 | c(NA, NA)*t1 + c(g5q1.4.thr1, g5q1.4.thr1)*t1\ng5q3.4 | c(NA, NA)*t1 + c(g5q3.4.thr1, g5q3.4.thr1)*t1\ng5q5.4 | c(NA, NA)*t1 + c(g5q5.4.thr1, g5q5.4.thr1)*t1\ng5q7.4 | c(NA, NA)*t1 + c(g5q7.4.thr1, g5q7.4.thr1)*t1\n\n## INTERCEPTS:\n\ng4q1.4 ~ c(nu.1, nu.1)*1 + c(0, 0)*1\ng4q3.4 ~ c(nu.2, nu.2)*1 + c(0, 0)*1\ng4q5.4 ~ c(nu.3, nu.3)*1 + c(0, 0)*1\ng4q7.4 ~ c(nu.4, nu.4)*1 + c(0, 0)*1\ng5q1.4 ~ c(nu.5, nu.5)*1 + c(0, 0)*1\ng5q3.4 ~ c(nu.6, nu.6)*1 + c(0, 0)*1\ng5q5.4 ~ c(nu.7, nu.7)*1 + c(0, 0)*1\ng5q7.4 ~ c(nu.8, nu.8)*1 + c(0, 0)*1\n\n## UNIQUE-FACTOR VARIANCES:\n\ng4q1.4 ~~ c(1, NA)*g4q1.4 + c(theta.1_1.g1, theta.1_1.g2)*g4q1.4\ng4q3.4 ~~ c(1, NA)*g4q3.4 + c(theta.2_2.g1, theta.2_2.g2)*g4q3.4\ng4q5.4 ~~ c(1, NA)*g4q5.4 + c(theta.3_3.g1, theta.3_3.g2)*g4q5.4\ng4q7.4 ~~ c(1, NA)*g4q7.4 + c(theta.4_4.g1, theta.4_4.g2)*g4q7.4\ng5q1.4 ~~ c(1, NA)*g5q1.4 + c(theta.5_5.g1, theta.5_5.g2)*g5q1.4\ng5q3.4 ~~ c(1, NA)*g5q3.4 + c(theta.6_6.g1, theta.6_6.g2)*g5q3.4\ng5q5.4 ~~ c(1, NA)*g5q5.4 + c(theta.7_7.g1, theta.7_7.g2)*g5q5.4\ng5q7.4 ~~ c(1, NA)*g5q7.4 + c(theta.8_8.g1, theta.8_8.g2)*g5q7.4\n\n## UNIQUE-FACTOR COVARIANCES:\n\ng5q1.4 ~~ c(NA, NA)*g5q7.4 + c(theta.8_5.g1, theta.8_5.g2)*g5q7.4\n\n## LATENT MEANS/INTERCEPTS:\n\ntype4 ~ c(alpha.1.g1, alpha.1.g2)*1 + c(0, NA)*1\n\n## COMMON-FACTOR VARIANCES:\n\ntype4 ~~ c(1, NA)*type4 + c(psi.1_1.g1, psi.1_1.g2)*type4\n", : lavaan WARNING: not all elements of the gradient are (near) zero; the optimizer may not have found a local solution; use lavInspect(fit, "optim.gradient") to investigate
I tried to run the same model by also freely estimating the threshold for that particular item for both groups and I got the results:
> # ================== third item ============== #
> test_partial_3<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016",group="group", group.equal=c("thresholds","loadings","intercepts"),
group.partial=c("type4=~g4q5.4", "g4q5.4|t1"),warn=T, return.fit=T, ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"),parameterization="theta", estimator="wlsmv", meanstructure=TRUE, std.lv=T )
> summary(test_partial_3, fit.measures=T, rsquare=T)
lavaan 0.6-3 ended normally after 159 iterations Optimization method NLMINB Number of free parameters 43Number of equality constraints 14
Number of observations per group 0 919 1 926 Estimator DWLS Robust Model Fit Test Statistic 57.106 62.068 Degrees of freedom 43 43 P-value (Chi-square) 0.073 0.030 Scaling correction factor 0.914 Shift parameter for each group: 0 -0.193 1 -0.194 for simple second-order correction (Mplus variant) Chi-square for each group: 0 28.977 31.498 1 28.129 30.569 Model test baseline model: Minimum Function Test Statistic 312.409 302.732 Degrees of freedom 56 56 P-value 0.000 0.000 User model versus baseline model: Comparative Fit Index (CFI) 0.945 0.923 Tucker-Lewis Index (TLI) 0.928 0.899 Robust Comparative Fit Index (CFI) NA Robust Tucker-Lewis Index (TLI) NA Root Mean Square Error of Approximation: RMSEA 0.019 0.022 90 Percent Confidence Interval 0.000 0.031 0.007 0.033 P-value RMSEA <= 0.05 1.000 1.000 Robust RMSEA NA 90 Percent Confidence Interval NA NA Standardized Root Mean Square Residual: SRMR 0.043 0.043 Parameter Estimates: Information Expected Information saturated (h1) model Unstructured Standard Errors Robust.sem Group 1 [0]: Latent Variables: Estimate Std.Err z-value P(>|z|) type4 =~ g4q1.4 (l.1_) 0.107 0.051 2.097 0.036 g4q3.4 (l.2_) 0.369 0.073 5.025 0.000 g4q5.4 (l.3_) 0.514 0.098 5.275 0.000 g4q7.4 (l.4_) 0.452 0.082 5.526 0.000 g5q1.4 (l.5_) 0.606 0.110 5.494 0.000 g5q3.4 (l.6_) 0.346 0.079 4.384 0.000 g5q5.4 (l.7_) 0.291 0.074 3.917 0.000 g5q7.4 (l.8_) -0.024 0.024 -1.003 0.316 Covariances: Estimate Std.Err z-value P(>|z|) .g5q1.4 ~~ .g5q7.4 (t.8_) -0.249 0.061 -4.072 0.000 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.4 (nu.1) 0.000 .g4q3.4 (nu.2) 0.000 .g4q5.4 (nu.3) 0.000 .g4q7.4 (nu.4) 0.000 .g5q1.4 (nu.5) 0.000 .g5q3.4 (nu.6) 0.000 .g5q5.4 (nu.7) 0.000 .g5q7.4 (nu.8) 0.000 type4 (a.1.) 0.000 Thresholds: Estimate Std.Err z-value P(>|z|) g41.4|1 (g41.) -0.417 0.043 -9.723 0.000 g43.4|1 (g43.) -0.980 0.056 -17.424 0.000 g45.4|1 (g45.) -0.002 0.047 -0.033 0.974 g47.4|1 (g47.) -0.562 0.050 -11.161 0.000 g51.4|1 (g51.) -0.244 0.049 -4.955 0.000 g53.4|1 (g53.) 0.141 0.043 3.257 0.001 g55.4|1 (g55.) -0.102 0.041 -2.472 0.013 g57.4|1 (g57.) 0.379 0.042 8.919 0.000 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.4 (t.1_) 1.000 .g4q3.4 (t.2_) 1.000 .g4q5.4 (t.3_) 1.000 .g4q7.4 (t.4_) 1.000 .g5q1.4 (t.5_) 1.000 .g5q3.4 (t.6_) 1.000 .g5q5.4 (t.7_) 1.000 .g5q7.4 (t.8_) 1.000 type4 (p.1_) 1.000 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.4 0.994 g4q3.4 0.938 g4q5.4 0.889 g4q7.4 0.911 g5q1.4 0.855 g5q3.4 0.945 g5q5.4 0.960 g5q7.4 1.000 R-Square: Estimate g4q1.4 0.011 g4q3.4 0.120 g4q5.4 0.209 g4q7.4 0.170 g5q1.4 0.268 g5q3.4 0.107 g5q5.4 0.078 g5q7.4 0.001 Group 2 [1]: Latent Variables: Estimate Std.Err z-value P(>|z|) type4 =~ g4q1.4 (l.1_) 0.107 0.051 2.097 0.036 g4q3.4 (l.2_) 0.369 0.073 5.025 0.000 g4q5.4 (l.3_) 0.134 0.048 2.779 0.005 g4q7.4 (l.4_) 0.452 0.082 5.526 0.000 g5q1.4 (l.5_) 0.606 0.110 5.494 0.000 g5q3.4 (l.6_) 0.346 0.079 4.384 0.000 g5q5.4 (l.7_) 0.291 0.074 3.917 0.000 g5q7.4 (l.8_) -0.024 0.024 -1.003 0.316 Covariances: Estimate Std.Err z-value P(>|z|) .g5q1.4 ~~ .g5q7.4 (t.8_) -0.222 0.126 -1.765 0.078 Intercepts: Estimate Std.Err z-value P(>|z|) .g4q1.4 (nu.1) 0.000 .g4q3.4 (nu.2) 0.000 .g4q5.4 (nu.3) 0.000 .g4q7.4 (nu.4) 0.000 .g5q1.4 (nu.5) 0.000 .g5q3.4 (nu.6) 0.000 .g5q5.4 (nu.7) 0.000 .g5q7.4 (nu.8) 0.000 type4 (a.1.) 0.625 0.303 2.064 0.039 Thresholds: Estimate Std.Err z-value P(>|z|) g41.4|1 (g41.) -0.417 0.043 -9.723 0.000 g43.4|1 (g43.) -0.980 0.056 -17.424 0.000 g45.4|1 (g45.) 0.087 0.055 1.564 0.118 g47.4|1 (g47.) -0.562 0.050 -11.161 0.000 g51.4|1 (g51.) -0.244 0.049 -4.955 0.000 g53.4|1 (g53.) 0.141 0.043 3.257 0.001 g55.4|1 (g55.) -0.102 0.041 -2.472 0.013 g57.4|1 (g57.) 0.379 0.042 8.919 0.000 Variances: Estimate Std.Err z-value P(>|z|) .g4q1.4 (t.1_) 2.989 1.240 2.410 0.016 .g4q3.4 (t.2_) 1.278 0.282 4.527 0.000 .g4q5.4 (t.3_) 1.000 .g4q7.4 (t.4_) 1.945 0.784 2.480 0.013 .g5q1.4 (t.5_) 7.431 5.059 1.469 0.142 .g5q3.4 (t.6_) 4.770 4.025 1.185 0.236 .g5q5.4 (t.7_) 4.889 4.002 1.222 0.222 .g5q7.4 (t.8_) 0.326 0.088 3.711 0.000 type4 (p.1_) 3.647 1.567 2.328 0.020 Scales y*: Estimate Std.Err z-value P(>|z|) g4q1.4 0.574 g4q3.4 0.751 g4q5.4 0.969 g4q7.4 0.610 g5q1.4 0.338 g5q3.4 0.438 g5q5.4 0.439 g5q7.4 1.747 R-Square: Estimate g4q1.4 0.014 g4q3.4 0.280 g4q5.4 0.062 g4q7.4 0.277 g5q1.4 0.153 g5q3.4 0.084 g5q5.4 0.059 g5q7.4 0.006
Based on the and notes https://crmda.dept.ku.edu/guides/21.LavaanSyntaxGuide/21.LavaanSyntaxGuide.pdf on lavaan I found at “The loadings and thresholds are both constrained to equality across groups “g”, allowing the scale of the ordinal indicators to be freely estimated in the second group” which I agree with, but I am thinking won’t freely estimating the thresholds for two groups will impact the degrees of freedom?
As in both the specifications (where I just freely estimated the loadings for the item g4q1.4 and where I freely estimated the loading as well as the threshold for item g4q5.4), the scaled degrees of freedom is 43.
I am curious if the scaled degrees of freedom don’t take in account the estimated values of the thresholds? Because the number of freely estimated and equal parameters are different in both the models (highlighted in green color).
Thanks in advance.
Regards,
Pavneet Kaur
Terrence Jorgensen
Pavneet Bharaj
Good evening Dr. Terrence. Sorry for the output. I wasn’t sure which parameter value would you require, so here I deleted some of the information in output that I felt might be unnecessary for my concern. I am working on checking the partial invariance of the model:
type4 <- 'type4=~ g4q1.4+ g4q3.4+ g4q5.4 + g4q7.4 + g5q1.4+ g5q3.4+ g5q5.4 + g5q7.4
g5q1.4 ~~ g5q7.4'
So, in this model I tried to assess for which item I need to freely estimate the factor loadings to attain the invariance at loadings, threshold, and intercepts level (Since my data is binary). For some of the items, when I freely estimated the loadings for both groups, I got results as:
test_partial_1<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016", group="group", group.equal = c("thresholds","loadings","intercepts"), group.partial = c("type4=~g4q1.4"), warn=T, return.fit=T, parameterization="theta", estimator="wlsmv", meanstructure=TRUE,std.lv=T, ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"))
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type4 =~
g4q1.4 (l.1_) 0.152 0.069 2.212 0.027
g4q3.4 (l.2_) 0.362 0.072 5.029 0.000
g4q5.4 (l.3_) 0.519 0.099 5.269 0.000
g4q7.4 (l.4_) 0.435 0.079 5.529 0.000
g5q1.4 (l.5_) 0.601 0.109 5.528 0.000
g5q3.4 (l.6_) 0.345 0.079 4.363 0.000
g5q5.4 (l.7_) 0.294 0.074 3.974 0.000
g5q7.4 (l.8_) -0.024 0.024 -1.014 0.311
Covariances:
Estimate Std.Err z-value P(>|z|)
.g5q1.4 ~~ .g5q7.4 (t.8_) -0.248 0.061 -4.070 0.000
Intercepts:
(all set to zero)
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.4|1 (g41.) -0.413 0.043 -9.537 0.000
g43.4|1 (g43.) -0.979 0.056 -17.524 0.000
g45.4|1 (g45.) 0.015 0.046 0.322 0.747
g47.4|1 (g47.) -0.562 0.050 -11.291 0.000
g51.4|1 (g51.) -0.248 0.049 -5.072 0.000
g53.4|1 (g53.) 0.130 0.043 3.049 0.002
g55.4|1 (g55.) -0.105 0.041 -2.559 0.011
g57.4|1 (g57.) 0.379 0.042 8.917 0.000
Variances:
(all set to 1)
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type4 =~
g4q1.4 (l.1_) 0.059 0.063 0.941 0.347
g4q3.4 (l.2_) 0.362 0.072 5.029 0.000
g4q5.4 (l.3_) 0.519 0.099 5.269 0.000
g4q7.4 (l.4_) 0.435 0.079 5.529 0.000
g5q1.4 (l.5_) 0.601 0.109 5.528 0.000
g5q3.4 (l.6_) 0.345 0.079 4.363 0.000
g5q5.4 (l.7_) 0.294 0.074 3.974 0.000
g5q7.4 (l.8_) -0.024 0.024 -1.014 0.311
Covariances:
Estimate Std.Err z-value P(>|z|)
.g5q1.4 ~~ .g5q7.4 (t.8_) -0.197 0.112 -1.764 0.078
Intercepts:
Estimate Std.Err z-value P(>|z|)
.(intercepts of items are all 0)
type4 (a.1.) 0.473 0.242 1.960 0.050
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.4|1 (g41.) -0.413 0.043 -9.537 0.000
g43.4|1 (g43.) -0.979 0.056 -17.524 0.000
g45.4|1 (g45.) 0.015 0.046 0.322 0.747
g47.4|1 (g47.) -0.562 0.050 -11.291 0.000
g51.4|1 (g51.) -0.248 0.049 -5.072 0.000
g53.4|1 (g53.) 0.130 0.043 3.049 0.002
g55.4|1 (g55.) -0.105 0.041 -2.559 0.011
g57.4|1 (g57.) 0.379 0.042 8.917 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.g4q1.4 (t.1_) 2.324 0.921 2.523 0.012
.g4q3.4 (t.2_) 1.158 0.236 4.902 0.000
.g4q5.4 (t.3_) 18.140 15.517 1.169 0.242
.g4q7.4 (t.4_) 1.612 0.580 2.781 0.005
.g5q1.4 (t.5_) 6.015 3.908 1.539 0.124
.g5q3.4 (t.6_) 4.381 3.515 1.246 0.213
.g5q5.4 (t.7_) 4.253 3.381 1.258 0.209
.g5q7.4 (t.8_) 0.320 0.085 3.761 0.000
type4 (p.1_) 3.402 1.379 2.467 0.014
But, when I tried to use the same code for some other items (within above model), I got this message:
test_partial_3<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016", group="group", parameterization="theta", group.equal = c("thresholds","loadings","intercepts"), estimator="wlsmv", meanstructure= TRUE, std.lv=T, group.partial=c("type4=~g4q5.4"),warn=T, return.fit=T, ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"))
Warning messages:
1: In lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats, : lavaan WARNING: The variance-covariance matrix of the estimated parameters (vcov)
does not appear to be positive definite! The smallest eigenvalue (= 2.197847e-14) is close to zero. This may be a symptom that the model is not identified.
2: In lavaan::lavaan(model = "## LOADINGS:\n\ntype4 =~ c(NA, NA)*g4q1.4 + c(lambda.1_1, lambda.1_1)*g4q1.4\ntype4 =~ c(NA, NA)*g4q3.4 + c(lambda.2_1, lambda.2_1)*g4q3.4\ntype4 =~ c(NA, NA)*g4q5.4 + c(lambda.3_1.g1, lambda.3_1.g2)*g4q5.4\ntype4 =~ c(NA, NA)*g4q7.4 + c(lambda.4_1, lambda.4_1)*g4q7.4\ntype4 =~ c(NA, NA)*g5q1.4 + c(lambda.5_1, lambda.5_1)*g5q1.4\ntype4 =~ c(NA, NA)*g5q3.4 + c(lambda.6_1, lambda.6_1)*g5q3.4\ntype4 =~ c(NA, NA)*g5q5.4 + c(lambda.7_1, lambda.7_1)*g5q5.4\ntype4 =~ c(NA, NA)*g5q7.4 + c(lambda.8_1, lambda.8_1)*g5q7.4\n\n## THRESHOLDS:\n\ng4q1.4 | c(NA, NA)*t1 + c(g4q1.4.thr1, g4q1.4.thr1)*t1\ng4q3.4 | c(NA, NA)*t1 + c(g4q3.4.thr1, g4q3.4.thr1)*t1\ng4q5.4 | c(NA, NA)*t1 + c(g4q5.4.thr1, g4q5.4.thr1)*t1\ng4q7.4 | c(NA, NA)*t1 + c(g4q7.4.thr1, g4q7.4.thr1)*t1\ng5q1.4 | c(NA, NA)*t1 + c(g5q1.4.thr1, g5q1.4.thr1)*t1\ng5q3.4 | c(NA, NA)*t1 + c(g5q3.4.thr1, g5q3.4.thr1)*t1\ng5q5.4 | c(NA, NA)*t1 + c(g5q5.4.thr1, g5q5.4.thr1)*t1\ng5q7.4 | c(NA, NA)*t1 + c(g5q7.4.thr1, g5q7.4.thr1)*t1\n\n## INTERCEPTS:\n\ng4q1.4 ~ c(nu.1, nu.1)*1 + c(0, 0)*1\ng4q3.4 ~ c(nu.2, nu.2)*1 + c(0, 0)*1\ng4q5.4 ~ c(nu.3, nu.3)*1 + c(0, 0)*1\ng4q7.4 ~ c(nu.4, nu.4)*1 + c(0, 0)*1\ng5q1.4 ~ c(nu.5, nu.5)*1 + c(0, 0)*1\ng5q3.4 ~ c(nu.6, nu.6)*1 + c(0, 0)*1\ng5q5.4 ~ c(nu.7, nu.7)*1 + c(0, 0)*1\ng5q7.4 ~ c(nu.8, nu.8)*1 + c(0, 0)*1\n\n## UNIQUE-FACTOR VARIANCES:\n\ng4q1.4 ~~ c(1, NA)*g4q1.4 + c(theta.1_1.g1, theta.1_1.g2)*g4q1.4\ng4q3.4 ~~ c(1, NA)*g4q3.4 + c(theta.2_2.g1, theta.2_2.g2)*g4q3.4\ng4q5.4 ~~ c(1, NA)*g4q5.4 + c(theta.3_3.g1, theta.3_3.g2)*g4q5.4\ng4q7.4 ~~ c(1, NA)*g4q7.4 + c(theta.4_4.g1, theta.4_4.g2)*g4q7.4\ng5q1.4 ~~ c(1, NA)*g5q1.4 + c(theta.5_5.g1, theta.5_5.g2)*g5q1.4\ng5q3.4 ~~ c(1, NA)*g5q3.4 + c(theta.6_6.g1, theta.6_6.g2)*g5q3.4\ng5q5.4 ~~ c(1, NA)*g5q5.4 + c(theta.7_7.g1, theta.7_7.g2)*g5q5.4\ng5q7.4 ~~ c(1, NA)*g5q7.4 + c(theta.8_8.g1, theta.8_8.g2)*g5q7.4\n\n## UNIQUE-FACTOR COVARIANCES:\n\ng5q1.4 ~~ c(NA, NA)*g5q7.4 + c(theta.8_5.g1, theta.8_5.g2)*g5q7.4\n\n## LATENT MEANS/INTERCEPTS:\n\ntype4 ~ c(alpha.1.g1, alpha.1.g2)*1 + c(0, NA)*1\n\n## COMMON-FACTOR VARIANCES:\n\ntype4 ~~ c(1, NA)*type4 + c(psi.1_1.g1, psi.1_1.g2)*type4\n", : lavaan WARNING: not all elements of the gradient are (near) zero; the optimizer may not have found a local solution; use lavInspect(fit, "optim.gradient") to investigate
I tried to run the same model by also freely estimating the threshold for that particular item for both groups and I got the results:
> test_partial_3<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016",group="group", group.equal=c("thresholds","loadings","intercepts"), return.fit=T, ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"),warn=T, parameterization="theta", estimator="wlsmv", meanstructure=TRUE, std.lv=T, group.partial=c("type4=~g4q5.4", "g4q5.4|t1"), )
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type4 =~
g4q1.4 (l.1_) 0.107 0.051 2.097 0.036
g4q3.4 (l.2_) 0.369 0.073 5.025 0.000
g4q5.4 (l.3_) 0.514 0.098 5.275 0.000
g4q7.4 (l.4_) 0.452 0.082 5.526 0.000
g5q1.4 (l.5_) 0.606 0.110 5.494 0.000
g5q3.4 (l.6_) 0.346 0.079 4.384 0.000
g5q5.4 (l.7_) 0.291 0.074 3.917 0.000
g5q7.4 (l.8_) -0.024 0.024 -1.003 0.316
Covariances:
Estimate Std.Err z-value P(>|z|)
.g5q1.4 ~~ .g5q7.4 (t.8_) -0.249 0.061 -4.072 0.000
Intercepts:
(all set to 0)
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.4|1 (g41.) -0.417 0.043 -9.723 0.000
g43.4|1 (g43.) -0.980 0.056 -17.424 0.000
g45.4|1 (g45.) -0.002 0.047 -0.033 0.974
g47.4|1 (g47.) -0.562 0.050 -11.161 0.000
g51.4|1 (g51.) -0.244 0.049 -4.955 0.000
g53.4|1 (g53.) 0.141 0.043 3.257 0.001
g55.4|1 (g55.) -0.102 0.041 -2.472 0.013
g57.4|1 (g57.) 0.379 0.042 8.919 0.000
Variances:
(all set to 1)
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
type4 =~
g4q1.4 (l.1_) 0.107 0.051 2.097 0.036
g4q3.4 (l.2_) 0.369 0.073 5.025 0.000
g4q5.4 (l.3_) 0.134 0.048 2.779 0.005
g4q7.4 (l.4_) 0.452 0.082 5.526 0.000
g5q1.4 (l.5_) 0.606 0.110 5.494 0.000
g5q3.4 (l.6_) 0.346 0.079 4.384 0.000
g5q5.4 (l.7_) 0.291 0.074 3.917 0.000
g5q7.4 (l.8_) -0.024 0.024 -1.003 0.316
Covariances:
Estimate Std.Err z-value P(>|z|)
.g5q1.4 ~~ .g5q7.4 (t.8_) -0.222 0.126 -1.765 0.078
Intercepts:
Estimate Std.Err z-value P(>|z|)
(0 for all items)
type4 (a.1.) 0.625 0.303 2.064 0.039
Thresholds:
Estimate Std.Err z-value P(>|z|)
g41.4|1 (g41.) -0.417 0.043 -9.723 0.000
g43.4|1 (g43.) -0.980 0.056 -17.424 0.000
g45.4|1 (g45.) 0.087 0.055 1.564 0.118
g47.4|1 (g47.) -0.562 0.050 -11.161 0.000
g51.4|1 (g51.) -0.244 0.049 -4.955 0.000
g53.4|1 (g53.) 0.141 0.043 3.257 0.001
g55.4|1 (g55.) -0.102 0.041 -2.472 0.013
g57.4|1 (g57.) 0.379 0.042 8.919 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.g4q1.4 (t.1_) 2.989 1.240 2.410 0.016
.g4q3.4 (t.2_) 1.278 0.282 4.527 0.000
.g4q5.4 (t.3_) 1.000
.g4q7.4 (t.4_) 1.945 0.784 2.480 0.013
.g5q1.4 (t.5_) 7.431 5.059 1.469 0.142
.g5q3.4 (t.6_) 4.770 4.025 1.185 0.236
.g5q5.4 (t.7_) 4.889 4.002 1.222 0.222
.g5q7.4 (t.8_) 0.326 0.088 3.711 0.000
type4 (p.1_) 3.647 1.567 2.328 0.020
Based on the and notes https://crmda.dept.ku.edu/guides/21.LavaanSyntaxGuide/21.LavaanSyntaxGuide.pdf on lavaan I found at “The loadings and thresholds are both constrained to equality across groups “g”, allowing the scale of the ordinal indicators to be freely estimated in the second group” which I agree with, but I am thinking won’t freely estimating the thresholds for two groups will impact the degrees of freedom?
As in both the specifications (where I just freely estimated the loadings for the item g4q1.4 and where I freely estimated the loading as well as the threshold for item g4q5.4), the scaled degrees of freedom is 43. I am curious if the scaled degrees of freedom don’t take in account the estimated values of the thresholds? Because the number of freely estimated and equal parameters are different in both the models (highlighted in green color).
Thanks in advance. Regards,
Pavneet Kaur
Terrence Jorgensen
Pavneet Kaur
Good Morning Dr. Terrence.
I replied to the previous question but checked today that my previous response has been deleted. Might be some mistake from my end. I am sorry for that. I have another concern in continuing the measurement invariance testing with the binary data I have been working with:
1. If I have need to test the partial invariance, do I need to freely estimate both “loadings” as well as “thresholds” altogether? (since my data is binary). Should I use test_partial_1 or test_partial_2?
For example:
type4 <- 'type4=~ g4q1.4+ g4q3.4+ g4q5.4 + g4q7.4 + g5q1.4+ g5q3.4+ g5q5.4 + g5q7.4'
partial invariance:
test_partial_1<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal = c("thresholds","loadings","intercepts"),
group.partial = c("type4=~g4q1.4", “g4q1.4|t1”), warn=T, return.fit=T,
parameterization="theta", estimator="wlsmv", meanstructure=TRUE,std.lv=T,
ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"))
test_partial_2<-measEq.syntax(type4, data=data, ID.cat="Wu.Estabrook.2016",
group="group", group.equal = c("thresholds","loadings","intercepts"),
group.partial = c("type4=~g4q1.4”), warn=T, return.fit=T,
parameterization="theta", estimator="wlsmv", meanstructure=TRUE,std.lv=T,
ordered=c("g4q1.4", "g4q3.4", "g4q5.4", "g4q7.4", "g5q1.4", "g5q3.4", "g5q5.4", "g5q7.4"))
Thanks in advance.
Terrence Jorgensen
1. If I have need to test the partial invariance, do I need to freely estimate both “loadings” as well as “thresholds” altogether? (since my data is binary). Should I use test_partial_1 or test_partial_2?
Pavneet Bharaj
Terrence Jorgensen
Can I just use "loading" as a parameter for partial invariance testing and not incorporate thresholds and intercepts in that?
Pavneet Bharaj
Sharon Zou
Error in GLIST.specify[[1]]$lambda[, ff] : subscript out of bounds
model <- '#latent factorsequity_Wave1 =~ Destination_Awareness_Wave1 + Destination_Attribute_Wave1 + Likert_Brand_2Personality_Wave1 + Brand_Credibility_Wave1 + Brand_Quality_Wave1 + Brand_Value_Wave1 + Brand_Loyalty_Wave1equity_Wave2 =~ Destination_Awareness_Wave2 + Destination_Attribute_Wave2 + Likert_Brand_Personality_Wave2 + Brand_Credibility_Wave2 + Brand_Quality_Wave2 + Brand_Value_Wave2 + Brand_Loyalty_Wave2'
#the 2 factors are repeated measureslongFacNames <- list(equity = c("equity_wave1", "equity_Wave2"))longIndNames <- list( Destination_Awareness = c( "Destination_Awareness_Wave1", "Destination_Awareness_Wave2" ), Destination_Attribute = c( "Destination_Attribute_Wave1", "Destination_Attribute_Wave2" ), Brand_Personality = c( "Likert_Brand_2Personality_Wave1", "Likert_Brand_Personality_Wave2" ), Brand_Credibility = c("Brand_Credibility_Wave1", "Brand_Credibility_Wave2"), Brand_Quality = c("Brand_Quality_Wave1", "Brand_Quality_Wave2"), Brand_Value = c("Brand_Value_Wave1", "Brand_Value_Wave2"), Brand_Layalty = c("Brand_Loyalty_Wave1", "Brand_Loyalty_Wave2") )
#configural modelsyntax.config <- measEq.syntax( configural.model = model, data = df2, ordered = c( "Destination_Awareness_Wave1", "Destination_Attribute_Wave1", "Likert_Brand_2Personality_Wave1", "Brand_Credibiilty_Wave1", "Brand_Quality_Wave1", "Brand_Value_Wave1", "Brand_Loyalty_Wave1", "Destination_Awareness_Wave2", "Destination_Attribute_Wave2", "Likert_Brand_Personality_Wave2", "Brand_Credibiilty_Wave2", "Brand_Quality_Wave2", "Brand_Value_Wave2", "Brand_Loyalty_Wave2" ), parameterization = "theta", ID.fac = "std.lv", ID.cat = "Wu.Estabrook.2016", return.fit = TRUE, longFacNames = longFacNames, long.equal = c("loadings", "intercepts") )Terrence Jorgensen
Error in GLIST.specify[[1]]$lambda[, ff] : subscript out of bounds
Matthias Vorberg
Hi Terence,
thanks for providing the measurement invariance functions! I have a question regarding partial invariance.
I want to examine the measurement invariance of a construct called "Demands". At both measurement points the construct was measured with three items each.
I have calculated a model for the configural invariance and a model for the metric invariance. The model comparison showed a significant difference (see comments in the code below). Therefore, I now want to examine the partial metric measurement invariance. I want to remove the constraint, i.e. the equivalence of the loadings, for the first item (AIZ01_1 and AIZ01_2 should not be forced to have equal loadings). I tried this by using long.partial with the default longIndNames. Maybe I did something wrong here (I never worked with longIndNames before and I am calculating the partial invariance for the first time).
I don't get any error message or warning, but the model comparison of the configural model with the metric model results in exactly the same output values as the comparison of the configural model with the partial metric model. This cannot be true! I therefore suspect that something went wrong when freeing the loadings of the first item between the two measurement points.
I would be very pleased about a hint to this!
Here is my commented code:
##### Measurement Invariance of "Demands"
### Configural invariance
model1 <- ' Demands_t1 =~ AIZ01_1 + AI02_1 + AI03_1
Demands_t2 =~ AIZ01_2 + AI02_2 + AI03_2 '
# Create list of variables
longFacNames <- list(Demands_both = c("Demands_t1","Demands_t2"))
# Configural model: no constraints across repeated measures
syntax.config <- measEq.syntax(configural.model = model1, data = dataFS,
longFacNames = longFacNames)
# Print a summary of model features
summary(syntax.config)
# Fit a model to the data
mod.config <- as.character(syntax.config)
fit.config <- cfa(mod.config, data = dataFS, parameterization = "theta")
### Metric invariance
syntax.metric <- measEq.syntax(configural.model = model1, data = dataFS,
longFacNames = longFacNames,
long.equal = c("loadings"))
# Print a summary of model features
summary(syntax.metric)
# Fit model to data
mod.metric <- as.character(syntax.metric)
fit.metric <- cfa(mod.metric, data = dataFS, parameterization = "theta")
# Compare model fits
compareFit(fit.config, fit.metric)
# Result is: There is a significant difference between both models; thus, partial metric invariance shall be examined
### Partical metric invariance
# Extract default longIndNames
syntax.metric@call$longIndNames
# These are the longIndNames:
# $._Demands_both_.ind.1
# Demands_t1 Demands_t2
# "AIZ01_1" "AIZ01_2"
# $._Demands_both_.ind.2
# Demands_t1 Demands_t2
# "AI02_1" "AI02_2"
# $._Demands_both_.ind.3
# Demands_t1 Demands_t2
# "AI03_1" "AI03_2"
# Constraint between "AIZ01_1" and "AIZ01_2" shall be freed --> "._Demands_both_.ind.1" is used in the long.partial argument
syntax.metric.partial <- measEq.syntax(configural.model = model1, data = dataFS,
longFacNames = longFacNames,
long.equal = c("loadings"), long.partial = c("._Demands_both_.ind.1 ~ 1"))
# Print a summary of model features
summary(syntax.metric.partial)
# Fit model to data
mod.metric.partial <- as.character(syntax.metric.partial)
fit.metric.partial <- cfa(mod.metric.partial, data = dataFS, parameterization = "theta")
# Compare model fits
compareFit(fit.config, fit.metric.partial)
Terrence Jorgensen
"._Demands_both_.ind.1 ~ 1""Demands_both =~ ._Demands_both_.ind.1"Matthias Vorberg
Matthias Vorberg
Hello together!
I would like to calculate the partial strict measurement invariance with grouping variable "gender", because in my model there was no strict measurement invariance when equating the residuals. But obviously I somehow misapplied the function "group.partial =", because when comparing the models "fit.scalar" and "fit.partialresidual" the result is the same as before when comparing the models "fit.scalar" and "fit.residual". I guess that the function "group.partial =" is simply ignored. What could be the reason for this?
Here is my code (at least for "fit.partialresidual" and the comparison with "fit.scalar"). Further down is the output.
-----------------------------
mod.cat <- '
Exp =~ TA + ML
Feed =~ DF + VF
Reflex =~ AR + SR
Intent =~ EI + II
Luvo =~ Exp + Feed + Reflex + Intent'
syntax.partialresidual <- measEq.syntax(configural.model = mod.cat, data = dataG2,
parameterization = "theta",
ID.fac = "ul",
group = "gender", missing="fiml", effect.coding = "loadings",
group.equal = c("loadings","intercepts","residuals"), group.partial = c("Exp =~ TA"))
summary(syntax.partialresidual)
mod.partialresidual <- as.character(syntax.partialresidual)
cat(mod.partialresidual)
## fit model to data
fit.partialresidual <- cfa(mod.partialresidual, data = dataG2, group = "gender",
parameterization = "theta")
## compare models
anova(fit.scalar, fit.partialresidual)
## summarize results
compareFit(fit.config, fit.metric, fit.scalar, fit.residual, fit.partialresidual)
-----------------------------
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
fit.scalar 40 75695 75985 513.68
fit.partialresidual 48 75708 75949 542.16 28.481 8 0.0003909 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
fit.config 32 75695 76033 497.52
fit.metric 36 75695 76009 505.51 7.9934 4 0.0918205 .
fit.scalar 40 75695 75985 513.68 8.1641 4 0.0857490 .
fit.residual 48 75708 75949 542.16 28.4812 8 0.0003909 ***
fit.partialresidual 48 75708 75949 542.16 0.0000 0
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
####################### Model Fit Indices ###########################
chisq df pvalue cfi tli aic bic rmsea srmr
fit.config 497.521† 32 .000 .953† .918 75694.906 76033.459 .097 .046†
fit.metric 505.514 36 .000 .953 .926 75694.899† 76009.270 .091 .047
fit.scalar 513.679 40 .000 .952 .933 75695.063 75985.251 .087 .048
fit.residual 542.160 48 .000 .950 .942† 75707.544 75949.368† .081† .050
fit.partialresidual 542.160 48 .000 .950 .942† 75707.544 75949.368† .081† .050
################## Differences in Fit Indices #######################
df cfi tli aic bic rmsea srmr
fit.metric - fit.config 4 0.000 0.008 -0.007 -24.189 -0.005 0.001
fit.scalar - fit.metric 4 0.000 0.007 0.164 -24.018 -0.004 0.000
fit.residual - fit.scalar 8 -0.002 0.009 12.481 -35.884 -0.006 0.002
fit.partialresidual - fit.residual 0 0.000 0.000 0.000 0.000 0.000 0.000
Terrence Jorgensen
- You set parameterization = "theta" without declaring any variables as ordered=
- If your indicators are ordinal (perhaps already of class c("ordered","factor") in the data.frame?), you cannot constrain intercepts or residuals without having constrained thresholds. With free thresholds, the intercepts and residuals will be fixed, so they will be equal by default already.
- You choose missing = "fiml", which is not available for ordinal outcomes.
- You set group.partial = c("Exp =~ TA"), which is a loading, not a residual variance. Furthermore, it is the first loading, so fixed to 1 using ID.fac = "ul". This would explain why no df were gained relative to the fully strict model.
- You set ID.fac = "ul" yet effect.coding = "loadings", the latter of which would imply ID.fac = "fx"
Matthias Vorberg
Thanks a lot, Terence, for clarifying which things are wrong in the script.
- You set parameterization = "theta" without declaring any variables as ordered=
- If your indicators are ordinal (perhaps already of class c("ordered","factor") in the data.frame?), you cannot constrain intercepts or residuals without having constrained thresholds. With free thresholds, the intercepts and residuals will be fixed, so they will be equal by default already.
In fact, I do not have ordinal data in the latent model, but numerical data (only the grouping variable gender is nominal). Therefore, I removed the command parameterization = "theta" now. If I understand it correctly, I do not need to define thresholds and do not need to check for threshold invariance when I have numeric data?
- You choose missing = "fiml", which is not available for ordinal outcomes.
Since I have numeric and no ordinal variables, I keep missing = "fiml".
- You set ID.fac = "ul" yet effect.coding = "loadings", the latter of which would imply ID.fac = "fx"
Indeed, I had first set ID.fac = "fx" to use the effect coding method. But then I got the warning message: "Higher-order factors detected. ID.fac set to "ul"."
So I thought I would set ID.fac = "ul" intentionally and effect.coding = "loadings" as a separate command.
First question on this point: When testing the measurement invariance, is ID.fac = "fx" the only correct option and does it work as effect.coding = "loadings" in a normal CFA? Or are there still differences, and I can combine both commands?
Second question on this point: If the above warning says ID.fac was automatically set to ul, is it still possible to use the effect coding method in a second-order model for the measurement invariance test? And if so, how?
- You set group.partial = c("Exp =~ TA"), which is a loading, not a residual variance. Furthermore, it is the first loading, so fixed to 1 using ID.fac = "ul". This would explain why no df were gained relative to the fully strict model.
Maybe it is a very stupid question, but how do I modify the residual variance of individual indicators for testing the partial scalar measurement invariance?
Also, in case I want to free a loading one time, and this would be the first loading, how would I do this? Is this generally not possible if ID.fac = "ul"? Or is it possible with ID.fac = "fx" instead?
Thanks for your help on this! If you have a hint where I can read more than to get the information only implicitly from ?measEq.syntax and ?lavOptions(), please let me know.
Terrence Jorgensen
I do not have ordinal data in the latent model, but numerical data (only the grouping variable gender is nominal). Therefore, I removed the command parameterization = "theta" now. If I understand it correctly, I do not need to define thresholds and do not need to check for threshold invariance when I have numeric data?
Indeed, I had first set ID.fac = "fx" to use the effect coding method. But then I got the warning message: "Higher-order factors detected. ID.fac set to "ul"."So I thought I would set ID.fac = "ul" intentionally and effect.coding = "loadings" as a separate command.
"In order to maintain generality, higher-order factors may include a mix of manifest and latent indicators, but they must therefore require ID.fac = "UL" to avoid complications with differentiating lower-order vs. higher-order (or mixed-level) factors."
First question on this point: When testing the measurement invariance, is ID.fac = "fx" the only correct option
can combine both commands?
is it still possible to use the effect coding method in a second-order model for the measurement invariance test? And if so, how?
Maybe it is a very stupid question, but how do I modify the residual variance of individual indicators for testing the partial scalar measurement invariance?
group.partial = c("x1~~x1","x5~~x5")Also, in case I want to free a loading one time, and this would be the first loading, how would I do this? Is this generally not possible if ID.fac = "ul"?
Or is it possible with ID.fac = "fx" instead?
Jess Step
Hi Terrence,
Thank you for creating this function. I have a question that I hope you can help with.
I want to conduct both group (sex) and longitudinal (two occasions – BL and FU2) measurement invariance for my Peer Problems data at the same time. Peer Problems has five indicators (loner, friend, popular, bullied, oldbest), is of ordinal data, and has three response options.
Because the data only has three response options, I have assumed the thresholds to be invariant and used this as the baseline model (I added a few lines in the syntax just to check this myself). Male sex and BL occasion were used as the reference groups.
Loading invariance was achieved, but scalar invariance was not, so I used the modification indices to free parameters sequentially and compared model fit. One of the MI suggestions was to free the parameter from the baseline group (male sex) at BL for ‘bullied’ but, as it is supposed to be the reference group, I went with the next suggestion which was baseline group at FU2 for ‘bullied’. This parameter was freely estimated in the baseline model, so it seemed OK to free it here.
I tried different combinations of measEq.syntax to free this parameter but it always seemed to either only free the female group or both males and females, so I decided to write the syntax myself so that it only frees the male group at FU2.
Is there a way to do this in measEq.syntax that I was missing? If not, is there a reason why I shouldn’t free this parameter? The syntax that I wrote works, but I wanted to check whether there would be a reason not to do this. I have been having problems with models I have been running that have been using these measurement invariance constraints, so I am trying to determine whether the problem lies here.
Thanks,
Jess
###############################################
### SEX AND TIME INVARIANCE - PEER PROBLEMS ###
###############################################
model.PP <- 'BL.PP =~ BL.loner + BL.friend + BL.popular + BL.bullied + BL.oldbest
FU2.PP =~ FU2.loner + FU2.friend + FU2.popular + FU2.bullied + FU2.oldbest'
longFacNames <- list(Time = c("BL.PP", "FU2.PP"))
longIndNames <- list(loner = c("BL.loner", "FU2.loner"),
friend = c("BL.friend", "FU2.friend"),
popular = c("BL.popular", "FU2.popular"),
bullied = c("BL.bullied", "FU2.bullied"),
oldbest = c("BL.oldbest", "FU2.oldbest") )
PP.config.syntax <- measEq.syntax(configural.model = model.PP, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex",
ID.fac = "std.lv", ID.cat = "Wu",
longFacNames = longFacNames,
longIndNames = longIndNames)
PP.config.syntax <- as.character(PP.config.syntax)
PP.config <- cfa(PP.config.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta", estimator = "WLSMV", group = "Sex")
summary(PP.config, fit.measures = T, standardized = T)
PP.thresholds.syntax <- measEq.syntax(configural.model = model.PP, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex", group.equal = "thresholds",
ID.fac = "std.lv", ID.cat = "Wu",
longFacNames = longFacNames, longIndNames = longIndNames,
long.equal = "thresholds")
PP.thresholds.syntax <- as.character(PP.thresholds.syntax)
PP.thresholds <- cfa(PP.thresholds.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta", estimator = "WLSMV", group = "Sex")
summary(PP.thresholds, fit.measures = T, standardized = T)
# Config and thresholds models are equivalent, so thresholds is used as the 'baseline'
##################################
### Weak invariance - loadings ###
##################################
PP.loadings.syntax <- measEq.syntax(configural.model = model.PP, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
ID.fac = "std.lv", ID.cat = "Wu",
group = "Sex", group.equal = c("thresholds", "loadings"),
longFacNames = longFacNames, longIndNames = longIndNames,
long.equal = c("thresholds", "loadings"))
PP.loadings.syntax <- as.character(PP.loadings.syntax)
PP.loadings <- cfa(PP.loadings.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex", estimator = "WLSMV")
summary(PP.loadings, fit.measures = T, standardized = T)
lavTestLRT(PP.thresholds, PP.loadings) # No significant difference
######################################
### Strong invariance - intercepts ###
######################################
PP.intercepts.syntax <- measEq.syntax(configural.model = model.PP, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
ID.fac = "std.lv", ID.cat = "Wu",
group = "Sex", group.equal = c("thresholds", "loadings", "intercepts"),
longFacNames = longFacNames, longIndNames = longIndNames,
long.equal = c("thresholds", "loadings", "intercepts"))
PP.intercepts.syntax <- as.character(PP.intercepts.syntax) # Intercepts all fixed to 0 (not just the reference group of BL males)
PP.intercepts <- cfa(PP.intercepts.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex", estimator = "WLSMV")
summary(PP.intercepts, fit.measures = T, standardized = T)
lavTestLRT(PP.loadings, PP.intercepts) # Significant difference
modificationIndices(PP.intercepts, sort = T, free.remove = F) # FU2.popular intercept in group 2 (Female)
PP.intercepts2.syntax <- measEq.syntax(configural.model = model.PP, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
ID.fac = "std.lv", ID.cat = "Wu",
group = "Sex", group.equal = c("thresholds", "loadings", "intercepts"),
group.partial = "FU2.popular ~ c(0, NA)*1",
longFacNames = longFacNames, longIndNames = longIndNames,
long.equal = c("thresholds", "loadings", "intercepts"))
PP.intercepts2.syntax <- as.character(PP.intercepts2.syntax)
PP.intercepts2 <- cfa(PP.intercepts2.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex", estimator = "WLSMV")
summary(PP.intercepts2, fit.measures = T, standardized = T)
lavTestLRT(PP.loadings, PP.intercepts2) # Significant difference
modificationIndices(PP.intercepts2, sort = T, free.remove = F) # FU2.popular in group 1
PP.intercepts3.syntax <- measEq.syntax(configural.model = model.PP, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
ID.fac = "std.lv", ID.cat = "Wu",
group = "Sex", group.equal = c("thresholds", "loadings", "intercepts"),
long.partial = "popular ~ 1",
longFacNames = longFacNames, longIndNames = longIndNames,
long.equal = c("thresholds", "loadings", "intercepts"))
PP.intercepts3.syntax <- as.character(PP.intercepts3.syntax)
# Note: Male and Female values for popular ~ 1 are equivalent - I checked whether it makes a difference to model fit to have separate values but it doesn't (not shown)
PP.intercepts3 <- cfa(PP.intercepts3.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex", estimator = "WLSMV")
summary(PP.intercepts3, fit.measures = T, standardized = T)
lavTestLRT(PP.loadings, PP.intercepts3) # Significant difference
modificationIndices(PP.intercepts3, sort = T, free.remove = F) # FU2.oldbest in group 2
PP.intercepts4.syntax <- measEq.syntax(configural.model = model.PP, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
ID.fac = "std.lv", ID.cat = "Wu",
group = "Sex", group.equal = c("thresholds", "loadings", "intercepts"),
group.partial = "FU2.oldbest ~ c(0, NA)*1",
long.partial = "popular ~ 1",
longFacNames = longFacNames, longIndNames = longIndNames,
long.equal = c("thresholds", "loadings", "intercepts"))
PP.intercepts4.syntax <- as.character(PP.intercepts4.syntax)
PP.intercepts4 <- cfa(PP.intercepts4.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex", estimator = "WLSMV")
summary(PP.intercepts4, fit.measures = T, standardized = T)
lavTestLRT(PP.loadings, PP.intercepts4) # Significant difference
modificationIndices(PP.intercepts4, sort = T)
# BL.bullied intercept for Males but it's supposed to be the reference group - FU2.bullied instead?
PP.intercepts5.syntax <- '## LOADINGS:
BL.PP =~ c(NA, NA)*BL.loner + c(lambda.1_1, lambda.1_1)*BL.loner
BL.PP =~ c(NA, NA)*BL.friend + c(lambda.2_1, lambda.2_1)*BL.friend
BL.PP =~ c(NA, NA)*BL.popular + c(lambda.3_1, lambda.3_1)*BL.popular
BL.PP =~ c(NA, NA)*BL.bullied + c(lambda.4_1, lambda.4_1)*BL.bullied
BL.PP =~ c(NA, NA)*BL.oldbest + c(lambda.5_1, lambda.5_1)*BL.oldbest
FU2.PP =~ c(NA, NA)*FU2.loner + c(lambda.1_1, lambda.1_1)*FU2.loner
FU2.PP =~ c(NA, NA)*FU2.friend + c(lambda.2_1, lambda.2_1)*FU2.friend
FU2.PP =~ c(NA, NA)*FU2.popular + c(lambda.3_1, lambda.3_1)*FU2.popular
FU2.PP =~ c(NA, NA)*FU2.bullied + c(lambda.4_1, lambda.4_1)*FU2.bullied
FU2.PP =~ c(NA, NA)*FU2.oldbest + c(lambda.5_1, lambda.5_1)*FU2.oldbest
## THRESHOLDS:
BL.loner | c(NA, NA)*t1 + c(BL.loner.thr1, BL.loner.thr1)*t1
BL.loner | c(NA, NA)*t2 + c(BL.loner.thr2, BL.loner.thr2)*t2
BL.friend | c(NA, NA)*t1 + c(BL.friend.thr1, BL.friend.thr1)*t1
BL.friend | c(NA, NA)*t2 + c(BL.friend.thr2, BL.friend.thr2)*t2
BL.popular | c(NA, NA)*t1 + c(BL.popular.thr1, BL.popular.thr1)*t1
BL.popular | c(NA, NA)*t2 + c(BL.popular.thr2, BL.popular.thr2)*t2
BL.bullied | c(NA, NA)*t1 + c(BL.bullied.thr1, BL.bullied.thr1)*t1
BL.bullied | c(NA, NA)*t2 + c(BL.bullied.thr2, BL.bullied.thr2)*t2
BL.oldbest | c(NA, NA)*t1 + c(BL.oldbest.thr1, BL.oldbest.thr1)*t1
BL.oldbest | c(NA, NA)*t2 + c(BL.oldbest.thr2, BL.oldbest.thr2)*t2
FU2.loner | c(NA, NA)*t1 + c(BL.loner.thr1, BL.loner.thr1)*t1
FU2.loner | c(NA, NA)*t2 + c(BL.loner.thr2, BL.loner.thr2)*t2
FU2.friend | c(NA, NA)*t1 + c(BL.friend.thr1, BL.friend.thr1)*t1
FU2.friend | c(NA, NA)*t2 + c(BL.friend.thr2, BL.friend.thr2)*t2
FU2.popular | c(NA, NA)*t1 + c(BL.popular.thr1, BL.popular.thr1)*t1
FU2.popular | c(NA, NA)*t2 + c(BL.popular.thr2, BL.popular.thr2)*t2
FU2.bullied | c(NA, NA)*t1 + c(BL.bullied.thr1, BL.bullied.thr1)*t1
FU2.bullied | c(NA, NA)*t2 + c(BL.bullied.thr2, BL.bullied.thr2)*t2
FU2.oldbest | c(NA, NA)*t1 + c(BL.oldbest.thr1, BL.oldbest.thr1)*t1
FU2.oldbest | c(NA, NA)*t2 + c(BL.oldbest.thr2, BL.oldbest.thr2)*t2
## INTERCEPTS:
BL.loner ~ c(0, 0)*1 + c(nu.1, nu.1)*1
BL.friend ~ c(0, 0)*1 + c(nu.2, nu.2)*1
BL.popular ~ c(0, 0)*1 + c(nu.3, nu.3)*1
BL.bullied ~ c(0, 0)*1 + c(nu.4, nu.4)*1
BL.oldbest ~ c(0, 0)*1 + c(nu.5, nu.5)*1
FU2.loner ~ c(0, 0)*1 + c(nu.1, nu.1)*1
FU2.friend ~ c(0, 0)*1 + c(nu.2, nu.2)*1
FU2.popular ~ c(NA, NA)*1 + c(nu.8, nu.8)*1
FU2.bullied ~ c(NA, 0)*1 + c(nu.9.g1, nu.9.g2)*1 # CHANGED HERE - MALES ESTIMATED
FU2.oldbest ~ c(0, NA)*1 + c(nu.5.g1, nu.5.g2)*1
## UNIQUE-FACTOR VARIANCES:
BL.loner ~~ c(1, NA)*BL.loner + c(theta.1_1.g1, theta.1_1.g2)*BL.loner
BL.friend ~~ c(1, NA)*BL.friend + c(theta.2_2.g1, theta.2_2.g2)*BL.friend
BL.popular ~~ c(1, NA)*BL.popular + c(theta.3_3.g1, theta.3_3.g2)*BL.popular
BL.bullied ~~ c(1, NA)*BL.bullied + c(theta.4_4.g1, theta.4_4.g2)*BL.bullied
BL.oldbest ~~ c(1, NA)*BL.oldbest + c(theta.5_5.g1, theta.5_5.g2)*BL.oldbest
FU2.loner ~~ c(NA, NA)*FU2.loner + c(theta.6_6.g1, theta.6_6.g2)*FU2.loner
FU2.friend ~~ c(NA, NA)*FU2.friend + c(theta.7_7.g1, theta.7_7.g2)*FU2.friend
FU2.popular ~~ c(NA, NA)*FU2.popular + c(theta.8_8.g1, theta.8_8.g2)*FU2.popular
FU2.bullied ~~ c(NA, NA)*FU2.bullied + c(theta.9_9.g1, theta.9_9.g2)*FU2.bullied
FU2.oldbest ~~ c(NA, NA)*FU2.oldbest + c(theta.10_10.g1, theta.10_10.g2)*FU2.oldbest
## UNIQUE-FACTOR COVARIANCES:
BL.loner ~~ c(NA, NA)*FU2.loner + c(theta.6_1.g1, theta.6_1.g2)*FU2.loner
BL.friend ~~ c(NA, NA)*FU2.friend + c(theta.7_2.g1, theta.7_2.g2)*FU2.friend
BL.popular ~~ c(NA, NA)*FU2.popular + c(theta.8_3.g1, theta.8_3.g2)*FU2.popular
BL.bullied ~~ c(NA, NA)*FU2.bullied + c(theta.9_4.g1, theta.9_4.g2)*FU2.bullied
BL.oldbest ~~ c(NA, NA)*FU2.oldbest + c(theta.10_5.g1, theta.10_5.g2)*FU2.oldbest
## LATENT MEANS/INTERCEPTS:
BL.PP ~ c(0, NA)*1 + c(alpha.1.g1, alpha.1.g2)*1
FU2.PP ~ c(NA, NA)*1 + c(alpha.2.g1, alpha.2.g2)*1
## COMMON-FACTOR VARIANCES:
BL.PP ~~ c(1, NA)*BL.PP + c(psi.1_1.g1, psi.1_1.g2)*BL.PP
FU2.PP ~~ c(NA, NA)*FU2.PP + c(psi.2_2.g1, psi.2_2.g2)*FU2.PP
## COMMON-FACTOR COVARIANCES:
BL.PP ~~ c(NA, NA)*FU2.PP + c(psi.2_1.g1, psi.2_1.g2)*FU2.PP'
PP.intercepts5 <- cfa(PP.intercepts5.syntax, data = outlong_data,
ordered = c("BL.loner", "BL.friend", "BL.popular", "BL.bullied", "BL.oldbest",
"FU2.loner", "FU2.friend", "FU2.popular", "FU2.bullied", "FU2.oldbest"),
parameterization = "theta",
group = "Sex", estimator = "WLSMV")
summary(PP.intercepts5, fit.measures = T, standardized = T)
Terrence Jorgensen
group.partial = "FU2.popular ~ c(0, NA)*1"
group.partial = "FU2.popular ~ 1"as you specify for long.partial=. I assume long.partial = "popular ~ 1" worked fine?
PP.intercepts2.syntax <- update(PP.intercepts.syntax,
change.syntax = c("FU2.popular ~ c(0, NA)*1",
"FU2.oldbest ~ c(0, NA)*1"))