First order and second order models and their loadings (CFA)

47 views

CFAFixloadingsecond-order

Skip to first unread message

Lisanne K.

unread,

Nov 19, 2018, 8:36:11 AM11/19/18

to lavaan

Hello everyone,

I am new to R and lavaan and have a few questions about a CFA I am running at the moment.

The original model is shown in picture 1.

Because F2 is only measured by two items I was wondering about the following:

I could either fix F2’s variance to one or I fix both loadings to one and freely estimate F2’s variance.

But why is it the case? I've heard something about "underidentification" when using only two Items but why do I need to fix both loadings to one? And what about the factor loadings belonging to the other factors which are measured by three items?

Do I need to fix all of them to one as well? (Maybe this question is reduntant as soon as I understand why it's important to fix both factor loadings).

I compared both and CFI, RMSEA and SRMR are slightly different.

In theory a more detailed version of the model is possible as well:

Now F1 is measured by two variables which by themselves are measured by two items each.

What about the factor loadings in this case?

This is my syntax, using the std.lv command:

Detailed <- '
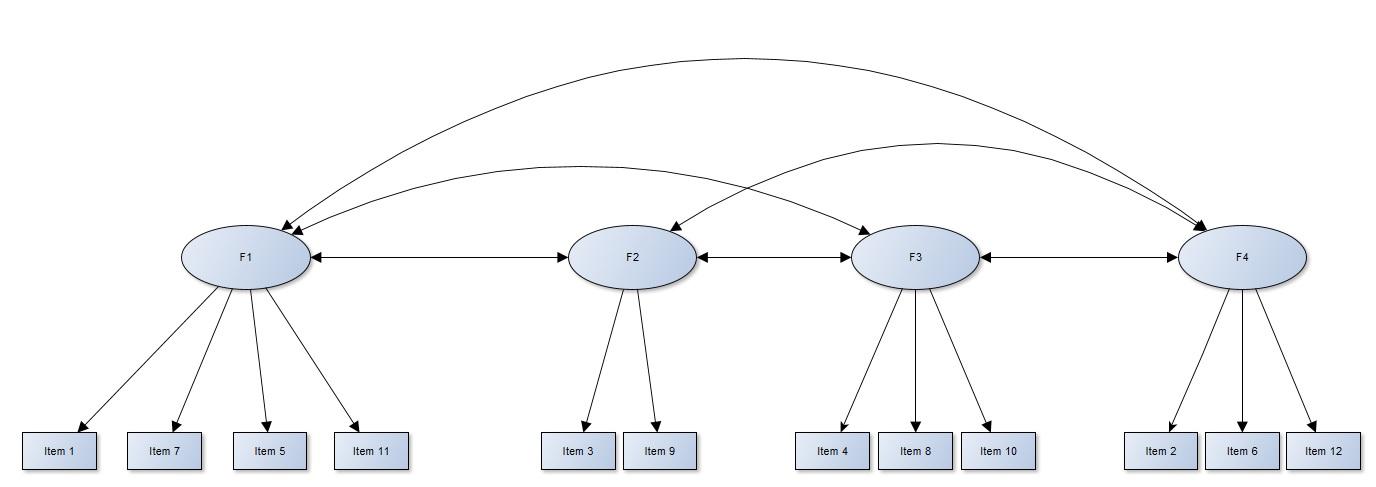
Lv1 =~ Item1 + Item 7
LV2 =~ Item5 + Item11
F3 =~ Item4 + Item8 + Item10
F4 =~ Item2 + Item6 + Item12
F2 =~ Item3 + Item 9

F1 =~ LV1 + LV2'

Detailed.fit <- sem(model= FirstOrderDetailed, data = exploration, std.lv =T, estimator= "mlr")
summary(FirstOrderDetailed.fit, fit.measures=TRUE, standardized=TRUE)

I can also think about the following model:

This is a syntax with fixing the LV's loadings to 1 but not for each item.

I also used the std.lv-command but I am unsure about this in this case:

HierarchicalDetailed <- '
### first-order variables
LV1 =~ 1*Item1 + Item 7
LV 2 =~ 1*Item5 + Item11

F3 =~ 1*Item4 + Item8 + Item10
F4 =~ 1*Item2 + Item6 + Item12
F2 =~ 1*Item3 + Item 9

## second-order models

F1 =~ 1*LV1+ 1*LV2
U1 =~ 1*F3 + F4 + F2

#Free estimation of variance*
F1 ~~ NA*F1
U1 ~~ Na*U1

## covariances
F1 ~~ U1
LV1 ~~ 0*LV2
LV1 ~~ 0*F3
LV1 ~~ 0*F4
LV1 ~~ 0*F2
LV2 ~~ 0*F3
LV2 ~~ 0*F4
LV2 ~~ 0*F2
F2 ~~ 0*F3
F2 ~~ 0*F4
F3 ~~ 0*F4

'
HierarchicalDetailed.fit <- sem(HierarchicalDetailed, data = exploration, estimator = "mlr", std.lv =T, missing = "fiml")
summary(HierarchicalDetailed.fit , fit.measures = T, standardized = T)

I am not quite sure if "std.lv=T" has been used right in this way?

And is it useful to use the "fiml" command?

These are the estimated values:

id lhs op rhs user block group free ustart exo label plabel start est se

1 1 LV1 =~ Item1 1 1 1 0 1 0 .p1. 1.000 1.000 0.000

2 2 LV1 =~ Item7 1 1 1 1 NA 0 .p2. 0.439 0.255 0.016

3 3 LV2 =~ Item5 1 1 1 0 1 0 .p3. 1.000 1.000 0.000

4 4 LV2 =~ Item11 1 1 1 2 NA 0 .p4. 0.168 0.101 0.018

5 5 F3 =~ Item4 1 1 1 0 1 0 .p5. 1.000 1.000 0.000

6 6 F3 =~ Item8 1 1 1 3 NA 0 .p6. 0.592 0.532 0.055

7 7 F3 =~ Item10 1 1 1 4 NA 0 .p7. 0.880 0.644 0.051

8 8 F4 =~ Item10 1 1 1 0 1 0 .p8. 1.000 1.000 0.000

9 9 F4 =~ Item10 1 1 1 5 NA 0 .p9. 0.745 0.295 0.031

10 10 F4 =~ Item12 1 1 1 6 NA 0 .p10. 0.537 0.191 0.027

11 11 F2 =~ Item3 1 1 1 0 1 0 .p11. 1.000 1.000 0.000

12 12 F2 =~ Item3 1 1 1 7 NA 0 .p12. 0.096 0.052 0.020

13 13 F1 =~ LV1 1 1 1 0 1 0 .p13. 1.000 1.000 0.000

14 14 F1 =~ LV2 1 1 1 0 1 0 .p14. 1.000 1.000 0.000

15 15 U1 =~ F3 1 1 1 0 1 0 .p15. 1.000 1.000 0.000

16 16 U1 =~ F4 1 1 1 8 NA 0 .p16. 1.000 0.537 0.033

17 17 U1 =~ F2 1 1 1 9 NA 0 .p17. 1.000 0.794 0.047

18 18 F1 ~~ F1 1 1 1 10 NA 0 .p18. 0.050 0.292 0.019

19 19 U1 ~~ U1 1 1 1 0 1 0 Na .p19. 1.000 1.000 0.000

20 20 F1 ~~ U1 1 1 1 11 NA 0 .p20. 0.000 0.045 0.032

21 21 LV1 ~~ LV2 1 1 1 0 0 0 .p21. 0.000 0.000 0.000

22 22 LV1 ~~ F3 1 1 1 0 0 0 .p22. 0.000 0.000 0.000

23 23 LV1 ~~ F4 1 1 1 0 0 0 .p23. 0.000 0.000 0.000

24 24 LV1 ~~ F2 1 1 1 0 0 0 .p24. 0.000 0.000 0.000

25 25 LV2 ~~ F3 1 1 1 0 0 0 .p25. 0.000 0.000 0.000

26 26 LV2 ~~ F4 1 1 1 0 0 0 .p26. 0.000 0.000 0.000

27 27 LV2 ~~ F2 1 1 1 0 0 0 .p27. 0.000 0.000 0.000

28 28 F3 ~~ F4 1 1 1 0 0 0 .p28. 0.000 0.000 0.000

29 29 F3 ~~ F2 1 1 1 0 0 0 .p29. 0.000 0.000 0.000

30 30 F4 ~~ F2 1 1 1 0 0 0 .p30. 0.000 0.000 0.000

31 31 Item1 ~~ Item1 0 1 1 12 NA 0 .p31. 0.356 -0.583 0.024

32 32 Item7 ~~ Item7 0 1 1 13 NA 0 .p32. 0.320 0.562 0.019

33 33 Item5 ~~ Item5 0 1 1 14 NA 0 .p33. 0.402 -0.496 0.027

34 34 Item11 ~~ Item11 0 1 1 15 NA 0 .p34. 0.428 0.843 0.028

35 35 Item4 ~~ Item4 0 1 1 16 NA 0 .p35. 0.578 0.639 0.107

36 36 Item8 ~~ Item8 0 1 1 17 NA 0 .p36. 0.504 0.695 0.061

37 37 Item10 ~~ Item10 0 1 1 18 NA 0 .p37. 0.499 0.538 0.067

38 38 Item10 ~~ Item10 0 1 1 19 NA 0 .p38. 0.418 -0.345 0.048

39 39 Item10 ~~ Item10 0 1 1 20 NA 0 .p39. 0.440 0.785 0.027

40 40 Item12 ~~ Item12 0 1 1 21 NA 0 .p40. 0.402 0.764 0.026

41 41 Item3 ~~ Item3 0 1 1 22 NA 0 .p41. 0.572 -0.344 0.058

42 42 Item3 ~~ Item3 0 1 1 23 NA 0 .p42. 0.508 1.012 0.030

43 43 LV1 ~~ LV1 0 1 1 0 1 0 .p43. 1.000 1.000 0.000

44 44 LV2 ~~ LV2 0 1 1 0 1 0 .p44. 1.000 1.000 0.000

45 45 F3 ~~ F3 0 1 1 0 1 0 .p45. 1.000 1.000 0.000

46 46 F4 ~~ F4 0 1 1 0 1 0 .p46. 1.000 1.000 0.000

47 47 F2 ~~ F 2 0 1 1 0 1 0 .p47. 1.000 1.000 0.000

48 48 Item1 ~1 0 1 1 24 NA 0 .p48. 3.792 3.792 0.021

49 49 Item7 ~1 0 1 1 25 NA 0 .p49. 3.986 3.987 0.020

50 50 Item5 ~1 0 1 1 26 NA 0 .p50. 3.744 3.744 0.022

51 51 Item11 ~1 0 1 1 27 NA 0 .p51. 2.996 2.997 0.023

52 52 Item4 ~1 0 1 1 28 NA 0 .p52. 2.731 2.730 0.027

53 53 Item8 ~1 0 1 1 29 NA 0 .p53. 2.727 2.727 0.025

54 54 Item10 ~1 0 1 1 30 NA 0 .p54. 2.812 2.813 0.025

55 55 Item10 ~1 0 1 1 31 NA 0 .p55. 3.392 3.393 0.023

56 56 Item10 ~1 0 1 1 32 NA 0 .p56. 3.514 3.516 0.023

57 57 Item12 ~1 0 1 1 33 NA 0 .p57. 3.329 3.330 0.022

58 58 Item3 ~1 0 1 1 34 NA 0 .p58. 2.948 2.948 0.026

59 59 Item3 ~1 0 1 1 35 NA 0 .p59. 3.368 3.367 0.025

60 60 LV1 ~1 0 1 1 0 0 0 .p60. 0.000 0.000 0.000

61 61 LV2 ~1 0 1 1 0 0 0 .p61. 0.000 0.000 0.000

62 62 F3 ~1 0 1 1 0 0 0 .p62. 0.000 0.000 0.000

63 63 F4 ~1 0 1 1 0 0 0 .p63. 0.000 0.000 0.000

64 64 F2 ~1 0 1 1 0 0 0 .p64. 0.000 0.000 0.000

65 65 F1 ~1 0 1 1 0 0 0 .p65. 0.000 0.000 0.000

66 66 U1 ~1 0 1 1 0 0 0 .p66. 0.000 0.000 0.000

Without using std.lv and fixing all loadings to one:

HierarchicalDetailed2 <- '
### first-order variables
LV1 =~ 1*Item1 + 1*Item 7
LV 2 =~ 1*Item5 + 1*Item11

F3 =~ 1*Item4 + Item8 + Item10
F4 =~ 1*Item2 + Item6 + Item12
F2 =~ 1*Item3 + 1*Item 9

For both variations I received the warning:

some estimated lv variances are negative

The models don't fit very well but at the moment I am more curious about understanding what to do about the loadings, why I get different results and which method is the best.

I am happy about any advice, literature or explanation in general.

Thank you,

Lisanne

Terrence Jorgensen

unread,

Nov 23, 2018, 11:04:06 AM11/23/18

to lavaan

I've heard something about "underidentification" when using only two Items but why do I need to fix both loadings to one?

When you only have 2 indicators (e.g., X and Y), the common variance is simply their covariance. You have 3 observed pieces of information (variance of X, variance of Y, and X-Y covariance), so you can only estimate 3 parameters (both residual covariances, and one parameter representing their common variance). Fixing both loadings to 1 means the common-factor variances is literally their covariance. Alternatively, you can fix the factor variance to 1 and constrain the loadings to equality, so they will be the square-root of the covariance.

When you have multiple factors, though, you can often (but not always) freely estimate both factor loadings (or only fixing the first loading to 1) because the covariance between items of different factors provides enough information to empirically identify the extra parameter. But if the factor covariances are not large (close to zero), then that extra information is not there, so the model becomes empirically underidentified.

http://dx.doi.org/10.1037/1082-989X.7.2.210

And what about the factor loadings belonging to the other factors which are measured by three items?

In that case, you have enough information to estimate all loadings (or fix only the first loading to 1). Any introductory SEM/CFA text should explain this.

I compared both and CFI, RMSEA and SRMR are slightly different.

The identification methods are statistically equivalent, so your fit should be the same. When you set std.lv=TRUE, you need to constrain the loadings to equality for the model to be equivalent to a model with a free factor variance and both loadings == 1.

Terrence D. Jorgensen

Assistant Professor, Methods and Statistics

Research Institute for Child Development and Education, the University of Amsterdam