How to enter binary observed outcome variable + scaling of latent variable?

[JL]

Dear all,

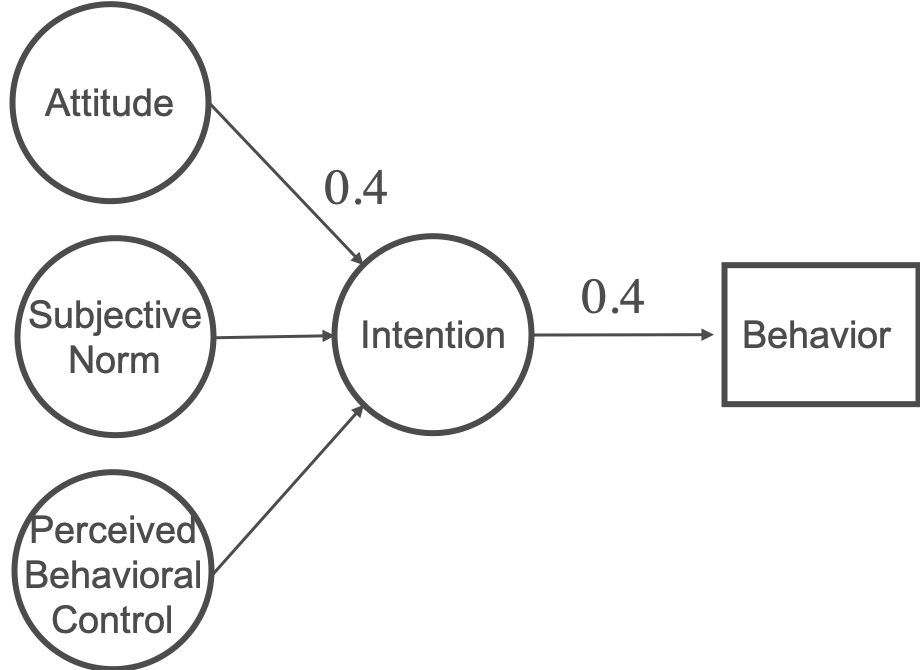
I am trying to run an SEM with the Theory of Planned Behavior. This is what my model looks like and that I want to test: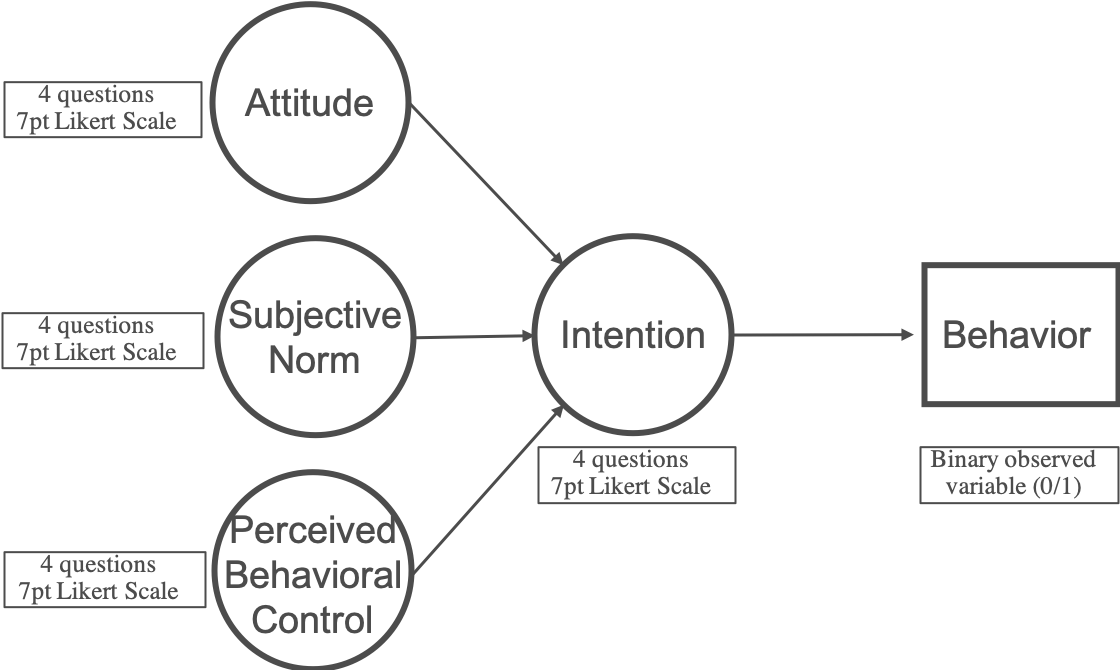

Attitude, Subjective Norm, Perceived Behavioral Control and Intention are latent variables, measured each by 4 indicators (questions) on a 7point likert scale. The Behavior is an observed binary variable (0=did not show behavior / 1 = did show behavior). 

I treat the likert-scale inputs as continuous variables, but I am unsure about how to deal with the real behavior (0/1) as binary variable? 

My code looks like:

mymodel <-  "

          attitude =~x1 + x2 + x3 + x4

          subjectivenorm =~  x5 + x6 + x7 + x8

          behcontrol =~  x9 + x10 + x11 + x12

          intention =~  x13 + x14 + x15 + x16

 

          intention ~ attitude + subjectivenorm + behcontrol

          behavior ~ intention"

In this context, I have two questions:

1. How do I enter my binary dependent variable (in the fit function)?
• I have seen that some use „ordered“ to treat these variables as ordered (ordinal) variables - is that the only way to do it? 
• e.g., fit <- sem(model = mymodel, data = df, ordered = "behavior") - like this?
• Why do I need to indicate my binary variable as ordinal variable, although it is categorical?
2. What is the interpretation of the betas?
• I am not quite sure how lavaan actually scales the latent variable? 
• How can I check the "values" of the latent variables? 
  

• If beta/ the regression coefficient of Attitude—>Intention is "0.4" - 
• are we talking about 1 unit increase in Attitude  —> "0.4" unit increase in Intention? (if so, what is the scale / units?)
• Or are we talking about 1 standard deviation increase in Attitude —> "0,4" standard deviation increase in Intention? (Where do I find the mean and SD of my latent variable?)
• How can I interpret a 0.4 from intention --> behavior?
• A 1 unit increase in Intention --> "0.4" unit increase in behavior? (Again here, the interpretation also depends on the scale of the latent variable intention - if intention as latent variable has the same likert scale of 1 to 7, it is something different as to whether if its scale was 0 to 1)

I first did quite some research online and in different books and simply could not find the answers I needed, so I appreciate very much any comment, advice, suggestion, reading tip, etc.

Thank you!

[Terrence Jorgensen]

• I have seen that some use „ordered“ to treat these variables as ordered (ordinal) variables - is that the only way to do it? 
• e.g., fit <- sem(model = mymodel, data = df, ordered = "behavior") - like this?

Yes

• Why do I need to indicate my binary variable as ordinal variable, although it is categorical?

Ordinal and nominal are both categorical.  Binary is a special case because it is arbitrary whether it is called nominal or ordinal.  SEM relies on assuming a latent response distribution (probit regression), so binary is simply considered ordinal for convenience.

https://doi.org/10.1080/10705510701758406

1. What is the interpretation of the betas?

Same as any regression slopes.  But the effect of intention on binary behavior is a probit regression slope, so its effect is in the scale of a normally distributed latent response (consult the standardized output to assume it is a z score, which is the default in lavaan, so it probably matches the unstandardized slope).

 

• I am not quite sure how lavaan actually scales the latent variable? 

You mean common factors?  The default is to use a marker variable, which you can override by fixing the latent variance to 1 using std.lv=TRUE

http://lavaan.ugent.be/tutorial/syntax2.html

• How can I check the "values" of the latent variables? 
  

You mean factor scores (see ?lavPredict) or the distributional parameters? (see summary() output)

• If beta/ the regression coefficient of Attitude—>Intention is "0.4" - are we talking about 1 unit increase in Attitude  —> "0.4" unit increase in Intention? (if so, what is the scale / units?)

Yes, and the units are arbitrary, defined relative to the (fixed or free) SD of the latent variables

• Or are we talking about 1 standard deviation increase in Attitude —> "0,4" standard deviation increase in Intention?

 That is the standardized solution.  See the "std.all" column of summary(fit, std=TRUE) output.

• (Where do I find the mean and SD of my latent variable?)

Variances are in the summary() output.

• How can I interpret a 0.4 from intention --> behavior?
• A 1 unit increase in Intention --> "0.4" unit increase in behavior? (Again here, the interpretation also depends on the scale of the latent variable intention - if intention as latent variable has the same likert scale of 1 to 7, it is something different as to whether if its scale was 0 to 1)

Again, it is a probit regression slope.  I would only both interpreting the standardized output, since the scale of the latent response is arbitrary (like the scale of common factors).

I first did quite some research online and in different books and simply could not find the answers I needed, so I appreciate very much any comment, advice, suggestion, reading tip, etc.

Nothing beats Ken Bollen's 1989 book.  It's pricey, but hopefully your institution provides access to it.

Terrence D. Jorgensen

Assistant Professor, Methods and Statistics

Research Institute for Child Development and Education, the University of Amsterdam

http://www.uva.nl/profile/t.d.jorgensen

[JL]

Thank you for your answers! One follow-up question:

1. What is the interpretation of the betas?

Same as any regression slopes.  But the effect of intention on binary behavior is a probit regression slope, so its effect is in the scale of a normally distributed latent response (consult the standardized output to assume it is a z score, which is the default in lavaan, so it probably matches the unstandardized slope).

 

In Lavaan - where do I find the beta-0? / what is the intercept for my probit regression? 

For the probit regression, my probability is Probability(Behavior = 1) = ϕ( β0 + β1*Intention)

The Beta-Coefficient alone does not tell me much, but I need the starting point to know the effect. How can I display my β0 or is it set to 0 by default? If so, then a person a person with an intention of 0 would have the probability of 0.5 to do the behavior? 

Happy about any help or experience! 

[Terrence Jorgensen]

In Lavaan - where do I find the beta-0? / what is the intercept for my probit regression? 

In the summary() output, look under the parameter section labeled "Intercepts:".  lavaan fixes latent-response intercepts to zero by default for identification, estimating instead the threshold(s), which for binary data are identical to -1 times the intercept if the threshold were instead fixed to zero.  If you want to exchange estimates, you can specify in the syntax:

behavior ~ intention
behavior ~ NA*1 # free the intercept
behavior | 0*t1 # fix the threshold to zero

[Kristina Mertens]

Hello everyone,

I am using the following model based on the UTAUT2 model in my thesis (so similar to you, JL):

Perceived Content Quality, Perceived Interactivity are latent variables influencing Performance Expectancy. Performance Expectancy, Effort Expectancy, Social Influence, Facilitating Conditions, Hedonic Motivation, Habit, Willingness to Pay, Trust, Safety Security and Need to Belong are latent variables as well, influencing Behavioral Intention. All latent variables are measured through multiple items, all scaled on a 7-point-Likert scale. 

Use Behavior is a binary variable with the outcomes "Yes" or "No". I want to see the influence of Behavorial Intention and Habit on Use Behaviour

This is my model:

model<-'
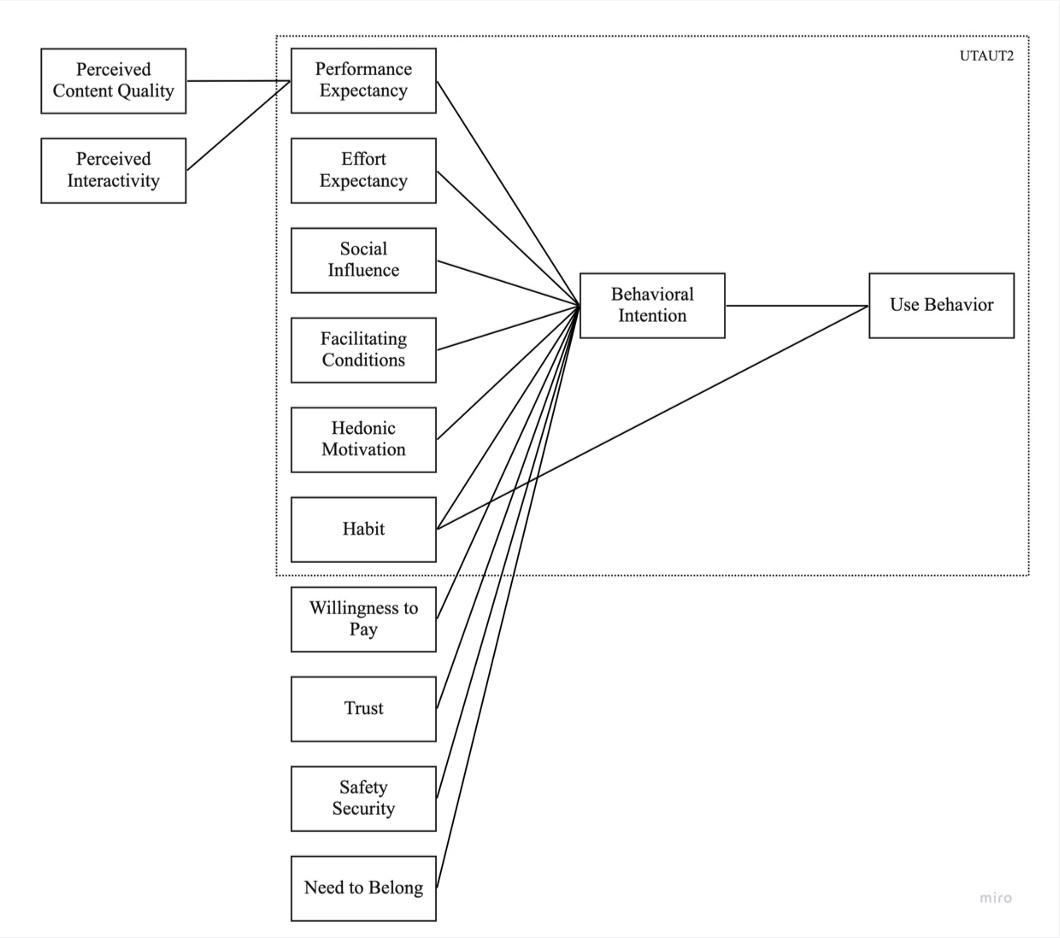
Quality=~PC01_01+PC01_02+PC01_03
Interactivity=~PI01_01+PI01_02+PI01_03+PI01_04+PI01_05
Performance=~PE01_01+PE01_02+PE01_03
Effort=~EE01_01+EE01_02+EE01_03+EE01_04
Influence=~SI01_01+SI01_02+SI01_03
Conditions=~FC01_01+FC01_02+FC01_03
Hedonism=~HM01_01+HM01_02+HM01_03
Habit=~HA01_01+HA01_02+HA01_03+HA01_04
Payment=~WP01_01+WP01_02+WP01_03
Trust=~TR01_01+TR01_02+TR01_03+TR01_04
Safety=~SS01_01+SS01_02+SS01_03+SS01_04
Belonging=~NB01_01+NB01_02+NB01_03+NB01_04+NB01_05+NB01_06+NB01_07+NB01_08+NB01_09+NB01_10
Intention=~BI01_01+BI01_02+BI01_03

Performance~Quality + Interactivity
Intention~Performance+Effort+Influence+Conditions+Hedonism+Habit+Payment+Trust+Safety+Belonging
Use~Intention
'

I tried using lavaan to run this SEM, but I failed plenty of times now. When I run my model without "Use", it works perfectly fine. As soon as I introduce "Use" as Use ~ Intention + Habit, I get the following error message:

fit <- sem(model = model, data = SocFeat,ordered = "Use", std.lv=TRUE)

Warning messages:
1: In lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats,  :
  lavaan WARNING:
    The variance-covariance matrix of the estimated parameters (vcov)
    does not appear to be positive definite! The smallest eigenvalue
    (= -9.659971e-11) is smaller than zero. This may be a symptom that
    the model is not identified.
2: In lav_object_post_check(object) :
  lavaan WARNING: covariance matrix of latent variables
                is not positive definite;
                use lavInspect(fit, "cov.lv") to investigate.

Before running the model and fit function, I also tried running this code: SocFeat$Use <- ordered(SocFeat$Use)

I'm not sure what to do, any advice on how I can fix this? I'm not sure where the error is.

Thanks!!

Kristina

[Terrence Jorgensen]

Warning messages:
1: In lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats,  :
  lavaan WARNING:
    The variance-covariance matrix of the estimated parameters (vcov)
    does not appear to be positive definite! The smallest eigenvalue
    (= -9.659971e-11) is smaller than zero. This may be a symptom that
    the model is not identified.
2: In lav_object_post_check(object) :
  lavaan WARNING: covariance matrix of latent variables
                is not positive definite;
                use lavInspect(fit, "cov.lv") to investigate.

These aren't errors, they are just warnings.  It is up to you to decide whether these are really problematic.  The first warning hints that there is some redundancy among estimated parameters, so perhaps multicollinearity could be a problem.  The second warning could be caused by a Heywood case or linear dependency among the latent covariance matrix.  Checking lavInspect(fit, "cor.lv") is also useful, in case the Heywood case is a correlation exceeding +/- 1.