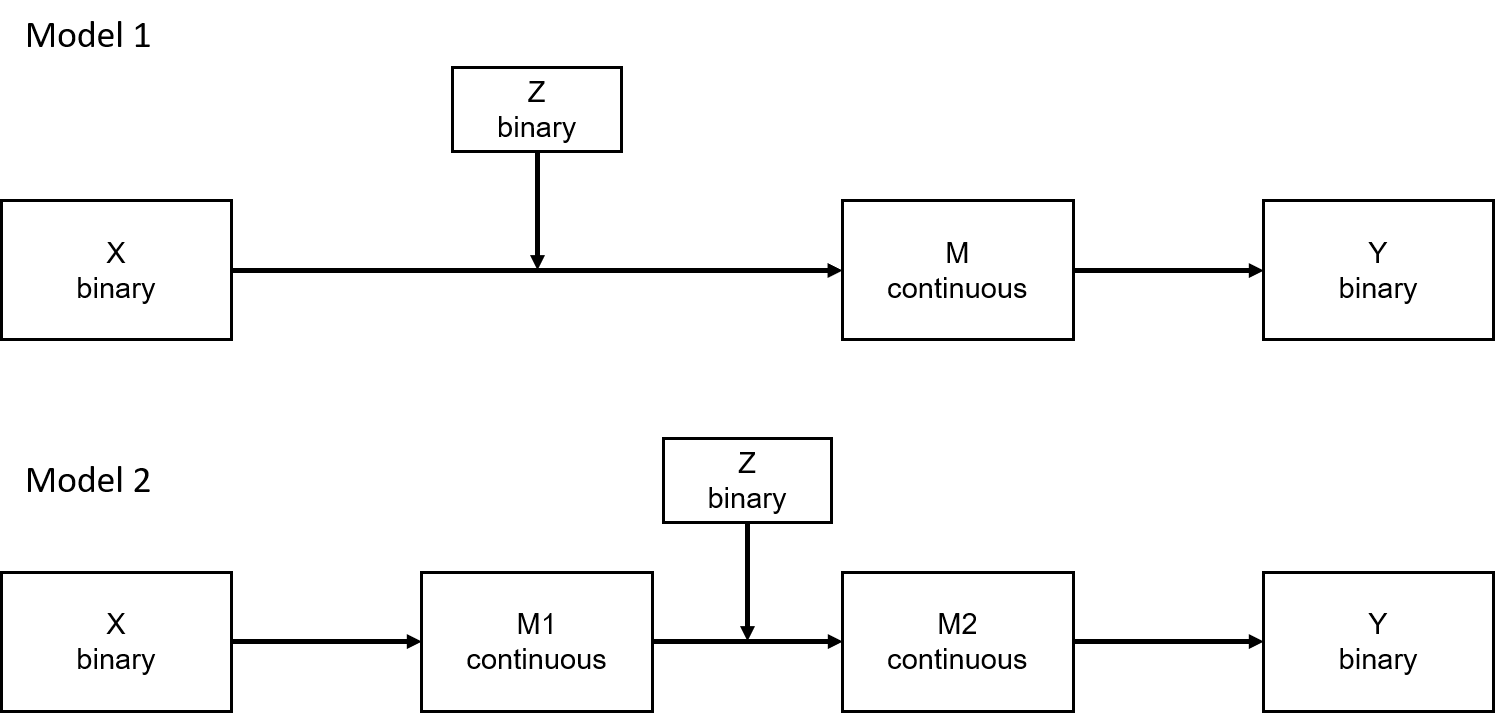
Moderated Mediation using dichotomous IV, mod, and DV + possible sequential mediation

[F.K. Ahrens]

Hi everyone,

I'd like to model the two models in the figure (among others) and don't get further, so hopefully someone has an idea for me. All data stems from an experimental design, thus it is not possible to change X or Z. For Y, I also have continuous versions of the DV but in simpler models, they did not work as good as the binary DVs. Also, I checked and the problem was not fixed by changing from binary to continuous DV.

Did it work at all?

Yes it did - I provided the code below. But I tried replicating the results of Model 1 using SPSS PROCESS macro and the lavaan output does not show the same results.

Therefore, I am doubting, whether the results of Model 2 are at all correct but I cannot model this in the PROCESS macro because it simply can't do that.

What I guess what the problem is? 

A combination of dichotomous IV, moderator and DV as well as the combination of using regression and logistic regression in the same model. The output suggests that the effects are driven by the moderator and not by the interaction as expected and shown using SPSS PROCESS macro.

Specifically, it does not help neither to declare the binary variables as ordered or to declare the binary variables as factors before calculating the interaction. Because then, lavaan simply cannot work with them anymore. Hence, I am not sure, whether it is at all possible to model this with lavaan and whether I should instead switch to MPlus for this.

Code for Model 1:

model_INFmodmed <-  ' 

# Equations

Y ~ con2*1 + cdash*X + b*M2_INF  

M2_INF ~ con1*1 + a1*X + a2*Z + az*XZ

# indirect and total effects on Z=0

ab0 := a1*b

total0 := ab0 + cdash

#indirect and total effects on Z=1

ab1 := (a1+az)*b

total1 := ab1 + cdash

# Index of moderated mediation

index := ab0 - ab1

          '

fit_INFmodmed <- sem(model_INFmodmed, data = Data)

summary(fit_INFmodmed)

Code for Model 2:

model_seqmodmed <- ' 

# Equations 

Y ~ con1*1 + cdash*X + d*M2_INF  

M1_GA ~ con2*1 + a*X 

M2_INF ~ con3*1 + b1*M1_GA + b2*Z + bz*M1_GA:Z

# indirect and total effects on Z=0

ab0 := a*b1

total0 := ab0 + cdash

#indirect and total effects on Z=1

ab1 := a*(b1+bz)

total1 := ab1 + cdash

# Index of moderated mediation

index := ab0 - ab1

          '

fit_seqmodmed <- sem(model_seqmodmed, data = Data)

summary(fit_seqmodmed)

I hope that someone has an idea, I ran out of ideas to solve this. Thanks a lot in advance!

[Terrence Jorgensen]

Did it work at all?

Yes it did - I provided the code below. But I tried replicating the results of Model 1 using SPSS PROCESS macro and the lavaan output does not show the same results.

Why would they?  PROCESS fits separate regression models then uses bootstrapping for SEs.  lavaan fits a simultaneous model then uses the delta method for SEs.

Terrence D. Jorgensen

Assistant Professor, Methods and Statistics

Research Institute for Child Development and Education, the University of Amsterdam

http://www.uva.nl/profile/t.d.jorgensen

[F.K. Ahrens]

Hi Terence,

thanks a lot for your reply. I was unaware of that statistical distinction between PROCESS and lavaan. Makes sense now that they do not replicate exactly.

Could you please let me know whether the approach to Model 2 is correct and/or how you would approach this?

Best,

Fabian

[Terrence Jorgensen]

Could you please let me know whether the approach to Model 2 is correct and/or how you would approach this?

I don't see anything necessarily wrong with your syntax, but I notice your model syntax regresses Y on X, yet your path diagram excludes that effect.  Was that intentional?  FYI, your user-defined "total effect" would include more indirect effects if you also meant to model (e.g.) direct effects of X on M2, or of M1 or Z on Y, which are also excluded from the diagram.

If Z is binary, you could perhaps simplify your specification and interpretation by using Z as a grouping variable to define a multigroup model.  You can then easily allow for Z to moderate all effects by virtue of estimating parameters separately in each group (Z=0 and Z=1).  You would label parameters unique for each group, and define your indirect effect of interest separately per group, making it easy to define "index" essentially the same way, as the difference between indirect effects in groups 0 and 1.

[F.K. Ahrens]

Thanks for your feedback Terrence!

I simplified the path diagram for the purpose here, so the additional regression was intentional. You are right that I did not include the additional indirect effects yet, thanks for raising this issue.

I already used Z as a grouping variable and it worked fine but I was interested in the interaction term as well, so that's why it got so messy to begin with.