growth curve model - problems with standardised coefficients
AV AV
Hi everyone,
I have recently started using lavaan to compute growth curve models with an intercept and a linear slope, for my three time points continuous variable, with a continous time-invariant covariate (COV).
The model has good fit parameters, but I get standardised values between intercept and c=variables higher than 1 - which is obviously impossible.
There is no error message, but something must have gone wrong, or at least needs changing.
Does anyone has any idea what?
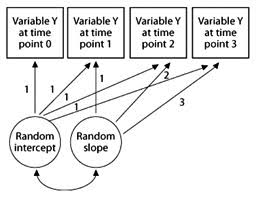
Here is my model:
'
# latent variable definitions
#intercept
eta_1 =~ 1*VAR_TIME1
eta_1 =~ 1*VAR_TIME2
eta_1 =~ 1*VAR_TIME3
#linear slope
eta_2 =~ 0*VAR_TIME1
eta_2 =~ 1*VAR_TIME2
eta_2 =~ 2*VAR_TIME3
# factor variances
eta_1 ~~ eta_1
eta_2 ~~ eta_2
# covariances among factors
eta_1 ~~ eta_2
# factor means
eta_1 ~ start(4)*1
eta_2 ~ start(2)*1
# manifest variances
VAR_TIME1~~ theta* VAR_TIME1
VAR_TIME2~~ theta* VAR_TIME2
VAR_TIME3~~ theta* VAR_TIME3
# manifest means
VAR_TIME1~ 0*1
VAR_TIME2~ 0*1
VAR_TIME3~ 0*1
# modification#
VAR_TIME2~ VAR_TIME1
VAR_TIME3~ VAR_TIME2
#regression of time-invariant covariate on intercept and slope factors
eta_1~COV
eta_2~ COV
#variance of covariate
COV ~~ COV
#means of covariate
COV ~ 1
'
And the problematic result:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 =~
VAR_TIME1 1.000 5.990 0.965
VAR_TIME2 1.000 5.990 1.155
VAR_TIME3 1.000 5.990 1.169
eta_2 =~
VAR_TIME1 0.000 0.000 0.000
VAR_TIME2 1.000 1.593 0.307
VAR_TIME3 2.000 3.185 0.622
Terrence Jorgensen
which is obviously impossible.
Andy Supple
--
You received this message because you are subscribed to the Google Groups "lavaan" group.
To unsubscribe from this group and stop receiving emails from it, send an email to lavaan+un...@googlegroups.com.
To post to this group, send email to lav...@googlegroups.com.
Visit this group at https://groups.google.com/group/lavaan.
To view this discussion on the web visit https://groups.google.com/d/msgid/lavaan/1a1c43fd-82be-4993-9c0d-7b681fbc7dfa%40googlegroups.com.
For more options, visit https://groups.google.com/d/optout.
AV AV
To unsubscribe from this group and stop receiving emails from it, send an email to lav...@googlegroups.com.
To post to this group, send email to lav...@googlegroups.com.
Visit this group at https://groups.google.com/group/lavaan.
To view this discussion on the web visit https://groups.google.com/d/msgid/lavaan/1a1c43fd-82be-4993-9c0d-7b681fbc7dfa%40googlegroups.com.
For more options, visit https://groups.google.com/d/optout.
Andy Supple
To unsubscribe from this group and stop receiving emails from it, send an email to lavaan+un...@googlegroups.com.
To post to this group, send email to lav...@googlegroups.com.
Visit this group at https://groups.google.com/group/lavaan.
To view this discussion on the web visit https://groups.google.com/d/msgid/lavaan/27402b5f-ab77-4189-842e-36e2e73fb73b%40googlegroups.com.
For more options, visit https://groups.google.com/d/optout.
AV AV
To view this discussion on the web visit https://groups.google.com/d/msgid/lavaan/27402b5f-ab77-4189-842e-36e2e73fb73b%40googlegroups.com.
For more options, visit https://groups.google.com/d/optout.



