4-coloring infinite strip
49 views
Skip to first unread message
Tom Sirgedas
Feb 2, 2021, 4:45:45 PM2/2/21
to Hadwiger-Nelson problem
I'm going to try to post here via e-mail
Tom Sirgedas
Feb 2, 2021, 5:06:55 PM2/2/21
to Hadwiger-Nelson problem
Hey, I wrote up my attempt at a "proof" that an infinite strip of width > 1 can't be 4-colored. I'm happy with the general idea, but I'm sure it needs some work. Anyways, I hope this is useful!
---
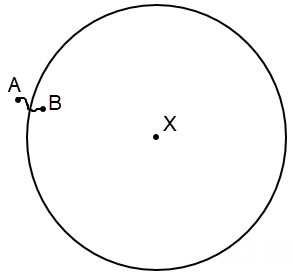
Let ε be a tiny value, such that any two points within distance ε have monochromatic paths that meet. The point at which they meet may be a third color.


---
Let ε be a tiny value, such that any two points within distance ε have monochromatic paths that meet. The point at which they meet may be a third color.
Examples:
In both of these examples points A and B are close together (within distance ε).
The left image shows only the colors of A, B and the associated paths. The right image shows a plane coloring. Here A is green and B is blue. The green and blue paths emanating from A and B respectively meet at point X. It's OK if point X is another color like yellow/purple.

Define COLORS(X) to be the set of all colors within distance ε of X.
Define COUNT(X) to be the size of that set.
Point X is a VERTEX if COLORS(X) >= 3 and if there is a monochromatic path from X to all points within distance ε of X. (The path is considered monochromatic regardless of the color of X).
---
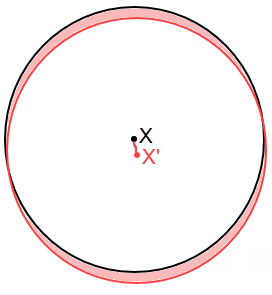
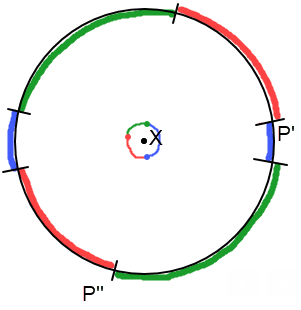
Observation 1: No monochromatic path can cross the unit circle around VERTEX X, if the path color is in COLORS(X)
Proof: Assume a monochromatic path AB exists. The locus of points a unit distance away from path AB envelopes X.
Since points of the same color can't appear a unit distance away, the assumption is false. QED.

---
Observation 2: Consider the unit circle around VERTEX X. Let X' be a nearby (distance = ε) point. The zone of exclusion for the path from X' to X is shown below.

Now let's consider what colors can be "adjacent" on each side of the circle.
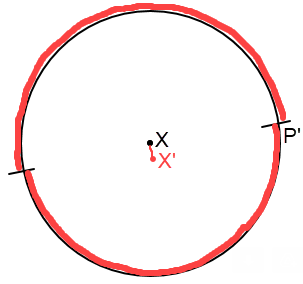
Here the red region is where red is ALLOWED. Note that the angle formed by X, X', P' is a right angle.

Now let's consider all red points distance ε from X. If the angle from X' to X'' is θ, then the two "allowed" arcs on the unit circle are 180-θ degrees each.

---
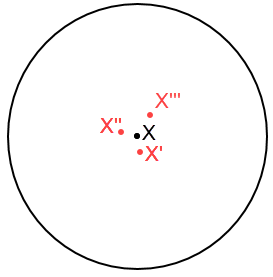
Observation 3:
If VERTEX X has nearby red points X', X'', and X''' that surround X, then the graph is "goofy" because VERTEX X and its vicinity could be replaced by a patch of red without creating new unit distance conflicts.
So, we can assume that the given graph is not "goofy".
So, we can assume that the given graph is not "goofy".

---
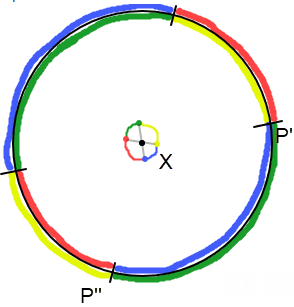
Observation 4: If COLORS(X) = 3, then the each point on X's unit circle is near (distance < ε) a point that can't be colored with those existing 3 colors.

Lemma: There's a continuous path around the unit circle which requires additional colors.
Example: Here the unit circle around VERTEX C (with colors blue, yellow, and red) requires green (the only other color) along the entire unit circle.

Lemma: You can't 4 color an infinite strip with width > 1 if there's a VERTEX X with COUNT(X) = 3.
Proof: the unit circle will require a continuous path for the fourth color, guaranteeing that two points with the fourth color are distance 1 apart.
---
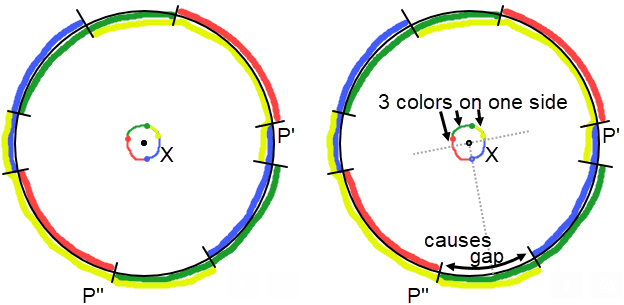
Observation 5: If VERTEX X has COLOR(X) = 4, then the unit circle may still have gaps.
These gaps occur when one "side" of the X has 3 colors.
These gaps occur when one "side" of the X has 3 colors.

The gaps are eliminated when the four colors are grouped into two pairs of colors (e.g. red & yellow, green & blue), such that when vertices A and B near X have X as a midpoint, then the colors of A and B are one of the color pairs.
Example:
Example:

Here, the existing 4 colors can complete the inside and outside parts adjacent to the unit circle around X. But, you can see that this forces 4 VERTEXes with COLOR = 4 on the unit circle.
---
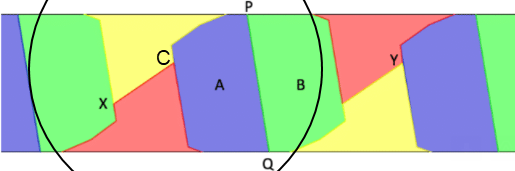
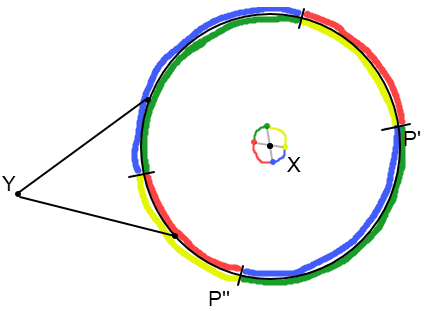
Observation 6: Point Y has unit distances to all four colors

Here's just an example of a partially 4-colored strip with width > 1. Observation 6 makes it clear that the partial coloring creates a conflict at Y:

Dömötör Pálvölgyi
Feb 3, 2021, 3:45:40 PM2/3/21
to Hadwiger-Nelson problem
Test message
Dömötör Pálvölgyi
Feb 3, 2021, 4:43:58 PM2/3/21
to Hadwiger-Nelson problem
This eps-distance implies monopath is a very interesting condition. I read everything and I believe that your argument is correct, except that it needs to be proven that Y also belongs to the strip.
To simplify the argument, I propose to assume that every tile is a polygon. I don't think it should be hard to prove that it possible to convert every tile-based coloring to a polygon-based coloring, at least if we assume that the number of tiles is finite in every bounded region.
ps. When you define VERTEX, then instead of COLORS you need COUNT, and I don't think that you need the additional condition about the monopath to distance eps points, because you already assumed that for every point.
On Tuesday, February 2, 2021 at 11:06:55 PM UTC+1 tsir...@gmail.com wrote:
Tom Sirgedas
Feb 3, 2021, 5:33:02 PM2/3/21
to Hadwiger-Nelson problem
Thanks for taking a look! I wasn't sure if I was completely off track or not, so I'm glad the idea makes sense.
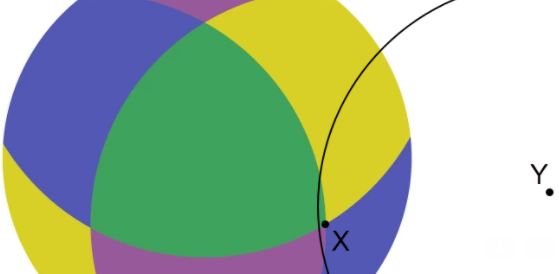
Also, the the image below satisfies the condition, but it doesn't make sense to have just one associated VERTEX. Hmm, actually, with my definition of VERTEX, there would be not VERTEXes here. Somehow ε needs to be forced to be smaller for this case. (I'm not sure how rigorous my reasoning needs to be??)

The tiles can't be polygons, they need curved edges. Note that X is touching a blue and a green tile. This forces the blue/green edge boundary to be curved.
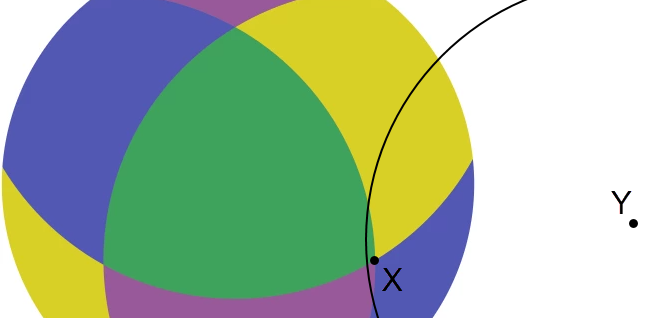

I think maybe the ["any two points within distance ε have monochromatic paths that meet"] condition can be used to show that a finite area can't have infinite tiles (though I'm not sure right now how that fact would be useful).
Re VERTEX:
Oh yeah, it should say COUNT(X) >= 3
I think the additional condition is important. There's the condition ["any two points within distance ε have monochromatic paths that meet"], but I want to say that the VERTEX *is* the meeting place for monochromatic paths.
Re VERTEX:
Oh yeah, it should say COUNT(X) >= 3
I think the additional condition is important. There's the condition ["any two points within distance ε have monochromatic paths that meet"], but I want to say that the VERTEX *is* the meeting place for monochromatic paths.
Also, the the image below satisfies the condition, but it doesn't make sense to have just one associated VERTEX. Hmm, actually, with my definition of VERTEX, there would be not VERTEXes here. Somehow ε needs to be forced to be smaller for this case. (I'm not sure how rigorous my reasoning needs to be??)

Tom Sirgedas
Feb 3, 2021, 8:03:14 PM2/3/21
to Hadwiger-Nelson problem
re "it needs to be proven that Y also belongs to the strip":
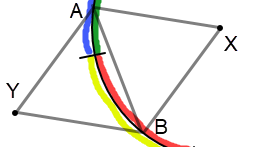
Pick Y, A, B, such that they are all on the strip.
COLORS(A) has at least two colors, on opposite sides of the unit circle
COLORS(B) has at least two colors, on opposite sides of the unit circle
COLORS(A), COLORS(B) can't have colors in common because they are a unit distance apart.

Pick Y, A, B, such that they are all on the strip.
COLORS(A) has at least two colors, on opposite sides of the unit circle
COLORS(B) has at least two colors, on opposite sides of the unit circle
COLORS(A), COLORS(B) can't have colors in common because they are a unit distance apart.
Y is a unit distance from all 4 colors.
I think this makes a lot of the reasoning in Observation 5/6 unnecessary.
I think this makes a lot of the reasoning in Observation 5/6 unnecessary.
Tom Sirgedas
Feb 3, 2021, 11:18:24 PM2/3/21
to Hadwiger-Nelson problem
Define MCOLORS(X) as the set of colors which have a monopath to point X (X is allowed to be a different color than the monopath) (This definition avoids ε, and won't count "stray" colors that happen to be close, but are disconnected from X)
Define MCOUNT(X) as the size of MCOLORS(X)
Note that VERTEX can be alternately defined as a point X such that MCOUNT(X) >= 3.
Define a TILE as the continuous region containing a single color.
Define an EDGE as the continuous boundary between two TILES. (NOTE: two tiles may share multiple disconnected edges)
Define an EDGE as the continuous boundary between two TILES. (NOTE: two tiles may share multiple disconnected edges)
Define MEDGE(X) as the EDGE which contains point X
Rule 5: Let's also require ε to be small enough such that all VERTEXes are more than 10ε apart.
(Not sure if this is necessary, but intuitively it's nice to have VERTEXes spaced far apart compared to ε)
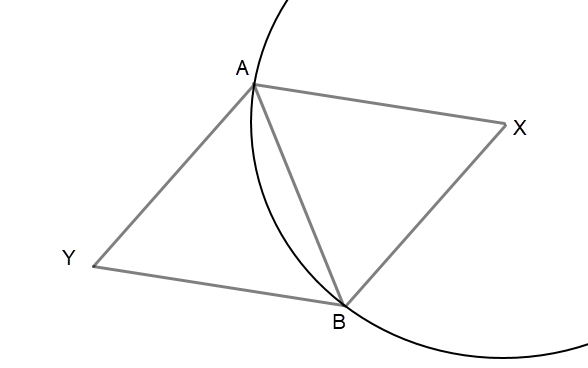
AB, AX, AY, BX, BY are all unit distance.
Observation 7: If MCOLORS(A) is a subset of MCOLORS(X), then MCOUNT(A) >= 2.
Proof: Both sides of the unit circle must be colored, but one color can't cross the unit circle (see Observation 1).
Proof: Both sides of the unit circle must be colored, but one color can't cross the unit circle (see Observation 1).
Observation 8: If MCOLORS(A) is a subset of MCOLORS(X), and MCOUNT(A) = 2, then MEDGE(A) lies on the X's unit circle.
Proof: Observation 1 tells us that the two colors can't cross the unit circle boundary. Both sides of the boundary must have a color. So the two colors lie on opposite sides of A, and have a boundary at A.
Repeat this logic for paths from A for which MCOLORS(A') is unchanged.
Observation 9: If MCOUNT(X) = 4, and MCOUNT(A) = 2 and MCOUNT(B) = 2, then 5 colors are needed to color Y, and the vicinity of A, B
Proof:
Proof:

A has 2 monopaths along the unit circle boundary, corresponding to MEDGE(A), with colors MCOLORS(A). This path extends on both sides of A (since MCOUNT(A) = 2) (here "both sides" means above and below A in the diagram).
Same for B.
There are unit distances between A's 2 paths and B's 2 paths, so 4 unique colors are required.
Y has unit distances to all 4 paths. So 5 colors are required!
Observation 10: A VERTEX X with MCOUNT(X) = 4 prevents a strip with width > 1 from being 4-colored.
Proof: We use Observation 9, noting that almost any choice of A,B,Y (properly distanced) works. Observation 7 guarantees that MCOUNT(A) >= 2, MCOUNT(B) >=2.
If MCOUNT(A) > 2 or MCOUNT(B) > 2, this means that A or B are a VERTEX and we can simply rotate about X a minuscule amount (say, ε radians).
Proof: We use Observation 9, noting that almost any choice of A,B,Y (properly distanced) works. Observation 7 guarantees that MCOUNT(A) >= 2, MCOUNT(B) >=2.
If MCOUNT(A) > 2 or MCOUNT(B) > 2, this means that A or B are a VERTEX and we can simply rotate about X a minuscule amount (say, ε radians).
A, B, Y can all be chosen such that they lie on the strip, since only a finite number of orientations of the "diamond" are prohibited, and the diamond has a width of 1.
Tom Sirgedas
Feb 3, 2021, 11:41:25 PM2/3/21
to Hadwiger-Nelson problem
Observation 11: Here's an alternate approach to proving a 4-color infinite strip with width > 1 can't have a VERTEX X with MCOUNT(X) = 3.
Let MCOLORS(X) = {red, green, blue}
The unit circle for X has length > 1, so MCOLORS() along the unit circle must exclude yellow for a some distance. So, there's an EDGE on the unit circle with colors {red, green}
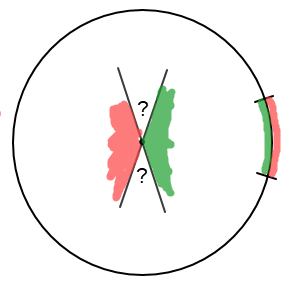

The ? regions can't be colored with red or green, so they must be filled with blue.
However, this means that blue "encloses" X, which isn't allowed (see Observation 3). QED.
---
So, Observations 10 & 11 together show that the strip can't have any VERTEXes.
Reply all
Reply to author
Forward
0 new messages
