Evaluating (a \times b)^2 using Geometric Algebra

[Ruvi Lecamwasam]

Let a and b be two vectors in \mathbb{R}^3, and let (a\times b) be their cross product. I want to simplify (a\times b)\cdot(a\times b) using geometric algebra. I know that

(a\times b)\cdot (a\times b)=a^2 b^2-(a\cdot b)^2,

where the square of a vector a^2 is given by a\cdot b.

To evaluate this using geometric algebra, we write 

a\times b=-I(a\wedge b),

where I is the pseudoscalar I^2=-1. Then:

(a\times b)\cdot(a\times b)=[-I(a\wedge b)]\cdot[-I(a\wedge b)].

We then simplify this using geometric algebra:

linearity

=[I(a\wedge b)]\cdot[I(a\wedge b)],

(Ia)\cdot b=I(a\wedge b)

=I[(a\wedge b)\wedge(I(a\wedge b))]

a\wedge(Ib)=I(a\cdot b)

=I^2(a\wedge b)\cdot(a\wedge b)

=I^2(a^2b^2-(a\cdot b)^2)

=-(a^2b^2-(a\cdot b)^2)

This however is the negative of the expected result. Can anyone see where I have gone wrong?

[Peeter Joot]

Hi Ruvi,

The text format of this forum makes it hard to follow what you are doing (despite having started this group, I think that https://math.stackexchange.com/ is currently a better option for many questions like this).

Here's how I'd show this:

Put everything into a grade zero selection operator to start with, so that you are free to commute the I's within that operator.  Then, once the I's have been eliminated, expand that scalar selection of the wedge product, using the distribution identity.

Peeter

[Manfred]

>> Put everything into a grade zero selection operator to start with, so that you are free to commute the I's within that operator.

I don't think that it is true that one can arbitrarily commute factors within the grade-0 projection operator.  One should also avoid applying the dot operator to anything except 1-vectors (unless one has define the extension in use, but it is unnecessary here).

Ruvi, I'm not going to decode your notation.  You can use the property that in three dimensions, 'I' anti-commutes with 1-vectors.  This can be used to prove that 'I' commutes with the wedge product of a pair of 1-vectors.  Also, the dot product of a 1-vector with itself is also equal to its square using the geometric product.

Here is my working:

   

Manfred

[Ruvi Lecamwasam]

Thank you both for your replies. I don't know how many conventions there are, but I'm following geometric algebra as introduced in Doran & Lasenby - Geometric Algebra for Physicists. 

Sorry for my earlier uncompiled LaTeX, I didn't realise I could send images in the group. My working was then

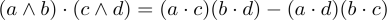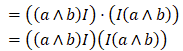
For the second-last line I used

,

which gives

.

However this seems to be the opposite (in sign) to Peeter's formula:

That would give me what I want. I'm guessing then that this is the issue? Is it some convention to do with the dot product on bivectors, and I need to use the scalar projection instead?

@Manfred, at least with the convention I'm used to, 'I' commutes with 1-vectors in three dimensions (though it doesn't make a difference to your proof)? Just wondering, what is your reasoning for replacing the dot product with the scalar product in

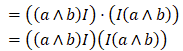
Thanks again everyone,

Ruvi

   

Manfred

--
You received this message because you are subscribed to the Google Groups "Geometric_Algebra" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geometric_alge...@googlegroups.com.
To post to this group, send email to geometri...@googlegroups.com.
Visit this group at https://groups.google.com/group/geometric_algebra.
For more options, visit https://groups.google.com/d/optout.

--

-Ruvi Lecamwasam

[Ruvi Lecamwasam]

My working doesn't seem to have sent, it should have been:

--

-Ruvi Lecamwasam

[Ruvi Lecamwasam]

Sorry to keep sending messages, I thought I would just conclude and say that I have realised my mistake. The formula

,

was incorrect, there should be a minus sign there. With that everything works.

Thanks again,

Ruvi

--

-Ruvi Lecamwasam

[Manfred]

Ruvi, sorry, (anti-)commuting of 'I' is not a matter of convention, I was just plain wrong: in three dimensions, 'I' always commutes with everything.
The dot product of a 1-vector with *itself* can be replaced with the geometric product: