Hex dome measurements

[mike wazowski]

Hi everyone, 

I was trying to make a paper model of a hex dome from a 6v class 1 geodesic dome.

I used these measurements :

B  0.1904769

E  0.1873834

F  0.1980126

H  0.2153537

I think the faces should be planar but on the actual paper model i coudnt align them.

Any ideas what i did wrong ? 

Taff do you have the measuremets for a class II hex dome like the second pic ? (maybe with a level base ?)

[Paul Kranz]

Mike:

The top pic looks like a 6-freq icosa (non-parallel pentagon sides), but the bottom one looks like an 8-freq dodeca (parallel pentagon sides). Please tell me you don't think they are the same thing!

Paul sends...

--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en

---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
For more options, visit https://groups.google.com/d/optout.

--

Very high regards,

 

Paul sends...

ReviveTheFlame.com

[Gerry in Quebec]

 

Hello Mike,

 

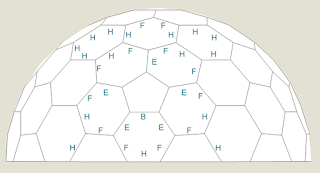
Given the chord factors you mentioned -- for 6v icosa, class I, method 1 -- only the pentagons (BBBBB) and central hexagons (HHHHHH) are planar. The remaining  "hexagons" (BDFHFD and FHFFHF) are not planar. 

 

Here's an alternative set of chord factors that will give you a level-base hemispheric dome, all of whose hex and pent faces are planar (a true polyhedron). It's the geometric dual of a 4v icosa, class II geosphere. So, not all vertices lie exactly on the surface of the surrounding sphere; there are 3 slightly different radii.

 

B = 0.1964544

E = 0.1797097

F = 0.2015725

H = 0.2008482

I = 0.2228530

J = 0.4238917 (long struts along dome base)

 

Attached you'll find an annotated version of the diagram you posted. It includes an Antiprism/Antiview image.

 

Hope this helps.

- Gerry in Québec

[mike wazowski]

Thank you so much Gerry ! I cant wait to try out the new lenghts !

You just made my day !

 

[mike wazowski]

Hi paul, i know they're not the same, but i would like to make both models. And i cant find the formulas for the 8v class II dodecahedron 

On Friday, January 22, 2016 at 7:24:15 PM UTC+2, Paul Kranz wrote:

[mike wazowski]

Actualy isnt the second one a class II 8v icosahedron ? 

[Gerry in Quebec]

Hi again Mike,

A few minutes ago I posted chord factors for your second hex-pent pic -- then realized I had used the wrong reference radius. So I deleted that post. The revised jpg, attached, gives the chord lengths when the surrounding sphere's radius is 1 unit.

 

Good luck with your models.

- Gerry

On Friday, January 22, 2016 at 9:48:09 AM UTC-5, mike wazowski wrote:

[Hector Alfredo Hernández Hdez.]

V6 comes from Mexican Method V6

[Hector Alfredo Hernández Hdez.]

Dont sit flat :(

[mike wazowski]

Gerry you've been such a great help !!! 

If i may ask you another question, the polyhedron from above isnt a hemisphere, i conected the base triangles hopeing it would give me a flat base, sadly not the case. 

Do you have the cord factors for it to be a hemisphere thus having a flat base ?

I'm pretty new at polyhedra geometry, would love one day to know how to make all these calculations.

Thanks again Gerry ! Very much apreciated !

[mike wazowski]

Hi Hector, thanks for the chord factors and pic, are all the faces planar ? to bad the base isnt flat :( 

I will have to read a book on the diferent methods used, cause i still dont understand why anyone would use the Mexican method when the method 1 is much easier and makes a flat base. 

[Hector Alfredo Hernández Hdez.]

The faces are planar?, I dont think so :(

2016-01-22 22:08 GMT-07:00 mike wazowski <docuin...@gmail.com>:

Hi Hector, thanks for the chord factors and pic, are all the faces planar ? to bad the base isnt flat :( 

I will have to read a book on the diferent methods used, cause i still dont understand why anyone would use the Mexican method when the method 1 is much easier and makes a flat base. 

[Gerry in Quebec]

Hi Mike,

You'll need the internal face angles of the hexes to draw and cut them from cardboard or heavy paper. See the attached jpg. The diagrams aren't to scale -- they're just to show you the locations of the various angles.

- Gerry

[Ken G. Brown]

If you orient the icosahedron edge to zenith, there is a natural flat equatorial plane, at least for the alternate breakdown based on the 60 isosceles triangles.

Ken G. Brown

On Jan 22, 2016, at 22:08, mike wazowski <docuin...@gmail.com> wrote:

Hi Hector, thanks for the chord factors and pic, are all the faces planar ? to bad the base isnt flat :( 

I will have to read a book on the diferent methods used, cause i still dont understand why anyone would use the Mexican method when the method 1 is much easier and makes a flat base. 

[mike wazowski]

Hi Gerry,

Thanks again mate ! I was gonna draw them without taking in consideration the angles , just the leghts, using a compas, but now i can make them perfect !

I will send you a pic of the paper model once it's done !

 

 

 

[mike wazowski]

Thanks Ken, i didnt know that.

[Gerry in Quebec]

Mike & Ken,

Maybe like this?

- Gerry

On Sunday, January 24, 2016 at 4:49:59 AM UTC-5, mike wazowski wrote:

[Gerry in Quebec]

Oops, the last set of images I posted for the dual of the 4v icosa was missing one sector of the dome. Here's the corrected set.

- Gerry

[Gerry in Quebec]

Mike,

The attached diagram includes both the face angles and chord factors of the second hex-pent dome you were interested, namely the dual of a 4v icosa, class I. (In anearlier post, I provided only the chord factors.) As Ken said, you can orient the dome to get a clean truncation along the equator. Your just have to bisect some pents and hexes.

 

By the way, the geosphere in the attached diagram is slightly different from the one in the 5-part collage I posted earlier today. It is the dual of a class I, 4v icosa based on method 1 and was generated by Small Stella, a polyhedral design and display program. The collage, generated by Antiprism, also depicts the dual of a class I, 4v icosa, but it seems to be based on some other method of subdivision -- I'm not sure which.

 

- Gerry

[Gerry in Quebec]

This time with the diagram attached....

[Ken G. Brown]

I believe the flat plane can be at the equator of the icosahedron with edge to zenith. These pics have the truncation plane higher up, it does not look like the truncation is at the equator.

Most likely requires the alternate breakdown.

Ken

--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en

---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
For more options, visit https://groups.google.com/d/optout.

<Dual-of-4v-icosa-classI-hemi.png>

[mike wazowski]

WOW Gerry that looks great !

I really have to start learning these 2 programs

THANK YOU Gerry ! 

[Adrian Rossiter]

Hi Gerry

On Sun, 24 Jan 2016, Gerry in Quebec wrote:
> Stella, a polyhedral design and display program. The collage, generated by
> Antiprism, also depicts the dual of a class I, 4v icosa, but it seems to be
> based on some other method of subdivision -- I'm not sure which.

The model uses the "window" method. There are equal central angles
for the divisions of the base triangle edge. The interior vertices
correspond to a meeting of three great circles, which intersect in
three pairs. The three intersections are calculated and the final
point is the centroid of these intesections, projected onto the
sphere.

The dual model can be made directly by name ('_d' for dual)

antiview geo_4_d

Faces of the same type can be coloured like this [image attached]

off_color -f S geo_4_d | antiview

Adrian.
--
Adrian Rossiter
adr...@antiprism.com
http://antiprism.com/adrian

[Gerry in Quebec]

Thanks for the explanation, Adrian. The "window" method is also called method 2. It's described by Joe Clinton in the math section of Domebook 2, page 107.

I've added the dual and face-colour commands to my growing file of Antiprism codes and tips!

 

Bryan (aka Bazil), take note, as I know you're interested in the window method.

 

- Gerry

[mike wazowski]

Gerry, i found this site :

http://dmccooey.com/polyhedra/DualGeodesicIcosahedron5.html

and the edege lenghts are diferent from what you wrote. 

Any chance these are the right ones ? Cause the paper model isnt looking to good so far, it's not quite round :( 

[Gerry in Quebec]

Hi Mike,

A few points about Goldberg polyhedron I {2,2} and dmcooey.com pages...

First, there is an infinite number of configurations -- combinations of chord lengths -- that will give you a spheroidal polyhedron with 122 faces (12 pentagons and 110 hexagons), 240 vertices and 360 edges. I doubt that the polyhedron depicted on the dmcooey.com has precisely the same geometry as the hemisphere I posted a few days ago. The latter has a very specific trait: the hemispheric dome sits perfectly flat if you split hexagons exactly in half along the base. I arrived at this layout by altering the position of some vertices in a 4v icosa, class II geodesic sphere and then generating its dual. The calculations were done in Excel and then I displayed the model in Antiview, a subprogram of Antiprism. So the model's geometry was not generated by Antiprism.

One possible reason your paper model may not look quite round so far is that it lacks the structural integrity you get with a triangulated dome. You need to use a very stiff, thick material to avoid "floppiness". (Big domes with hex-pent structures like the Eden Project biomes and the Montreal Biosphere have complementary support structures either fully or partially triangulated.)

In looking at various polyhedra on the dmcooey.com website, I see that I don't understand what this person is doing. He/she states in the data section under each 3D polyhedron model: "values below based on edge-scribed radius = 1". Sorry, but I don't know what that means.... perhaps Adrian can help here!

If you compare the website's volume values for 2v and 3v icosa geodesic spheres, the numbers are nearly identical: 4.188905... and 4.1889267... respectively. How can this be since a 3v is significantly closer to spherical than a 2v? The values are also significantly larger than those for a conventional 2v icosa geodesic sphere (3.6587) and a 3v icosa geodesic sphere, method 1 (3.9414). Again, how can this be? And the chord factors are completely different. So, the author of that website is not calculating various dimensions in any way I recognize.

If you like, I can use Antiprism's dual-generation subprogram to get the chord factors of an I (3,3) polyhedron but it won't necessarily sit flat at the equator. Let me know.

Looking forward to seeing pix of your models. Good luck.

- Gerry

[Gerry in Quebec]

Hi again Mike,

I've just double-checked the I {2,2} chord factors I posted on Jan. 22 and they all seem correct. I imported the model into SketchUp and used the tape measure to verify the 6 chord lengths. An image of the SketchUp version is attached.

- Gerry in Québec

On Friday, January 29, 2016 at 1:10:57 PM UTC-5, mike wazowski wrote:

[mike wazowski]

Thank you Gerry for looking into it, today i will try to finish the paper model and will post pics, but it isnt looking good and the problem isnt the material used or the structural integrity cause at a small scale that shouldnt be an issue and wouldnt need extra tension elements like the Eden domes. I really hope i'm not wrong. 

[Adrian Rossiter]

Hi Gerry

On Fri, 29 Jan 2016, Gerry in Quebec wrote:
> In looking at various polyhedra on the dmcooey.com website, I see that I
> don't understand what this person is doing. He/she states in the data
> section under each 3D polyhedron model: "values below based on edge-scribed
> radius = 1". Sorry, but I don't know what that means.... perhaps Adrian can
> help here!

He is saying that the edges are tangent to a unit sphere.

In Antiprism you could achieve this with the canonical form, e.g.
[image attached]

canonical geo_3_3_d | antiview


Allowing for a few seconds processing the edges are tangent to the
unit sphere to 15 decimal places.

canonical -n 10000 -l 20 geo_3_3_d | off_report -S D

[distances]
given_center = (0 0 0)
...
edge_min = 0.99999999999999634
edge_max = 1.0000000000000042
edge_avg = 1

[Gerry in Quebec]

Hi Adrian,
Thanks for explaining "edge-scribed radius" and its link to the canonical versions of polyhedra. Yesterday afternoon I was showing someone an unconventional wooden hub I had built for a 2v icosa dome. For easier construction I had altered the dome geometry to equalize all axial angles at 6-way and 4-way (base) vertices. Use of Antiprism's canonical feature just now has demonstrated that the doctored shape, which is less spherical than the regular dome shape in which all radii are of equal length, is none other than the canonical form of the 2v icosa.
- Gerry

[mike wazowski]

Here are the pics, first is the GP (2,2) next to a 4V 

 

[mike wazowski]

And Gerry i did follow to the letter your chord factors and angles. 

Last year i tried to make a GP only with regular hexagons and it looked just like this, in the sense that from abobe it's wasnt round but a pentagonal shape.

Any suggestions ? 

 

[Gerry in Quebec]

Hi Mike,

Nope....it doesn't look like the computer model. I did double-check the chord factors, and the computer model looks fine in both SketchUp and Antiprism. So, now I will go back and double-check the face angles. Sorry it didn't turn out as you'd hoped.

- Gerry

[Gerry in Quebec]

Hi Mike,

I double-checked the angle positions in the hex diagrams I posted against my original Excel file and everything looks okay. I also compared my calculated face angles with the SketchUp model and they match. So, I'm at a loss to explain why your paper model doesn't look as spherical as it should.... May I should buckle down and make a cardboard model :-)

- Gerry

On Saturday, January 30, 2016 at 6:58:33 AM UTC-5, mike wazowski wrote:

[mike wazowski]

I really hope you'll make a paper model cause i know 100% that you'll get the same result as me, since this is the 3rd hex dome i've tried.

I use paperboard (200grams) for the models.

Last year i sent George Hart and email regarding these measurements but he didnt reply :( 

Casue he makes lots of Goldberg models.

 

 

[mike wazowski]

I would really like to make a decent model for a GP (2,2) so that i can move on to the next project, a GP (3,3) which is the best looking one imo.

Like the one in the eden project or the one made by this guy :

https://www.youtube.com/watch?v=js3Bp_3glvY

But as you can see in the video, he also has the same problem, the dome isnt as sferical as it should be, probably cause all his hexagons are regular. 

 

[Dick Fischbeck]

Did you check Joe Clinton's paper?

http://45.79.160.8/technical/clintons-equal-central-angle-conjecture/

On Sat, Jan 30, 2016 at 1:03 PM, mike wazowski <docuin...@gmail.com> wrote:

I would really love to make a decent GP (2,2) so that i can move on to the next faze, GP (3,3) , which is the best looking one imo.

[Dick Fischbeck]

Also here:

https://docs.google.com/file/d/0B63MOsGa2dEwMkNzMUxRWXZ0YjQ/edit

[Gerry in Quebec]

Hi Mike,

I made a cardstock model. It turned out just as I expected. Three images attached.

- Gerry in Québec

[mike wazowski]

Hi Gerry,

Wow that looks so perfect !

I am such an idiot !  I drew the E edge  6mm longer ! so 60 times a 6mm error no wonder my model was crap.

I will redo it asap, you're a life saver Gerry !

Thanks so much for helping me out 

[Radu Sora]

I use acidome.ru for any icosa based dome. It also offers an inscribed or described "fullerene" (hexa+pentagons) solution up to V8, as I remember. Is it the same as Goldberg icosa solution? The faces look pretty flat to me, are they?

vineri, 22 ianuarie 2016, 16:48:09 UTC+2, mike wazowski a scris:

Hi everyone, 

I was trying to make a paper model of a hex dome from a 6v class 1 geodesic dome.

I used these measurements :

B  0.1904769

E  0.1873834

F  0.1980126

H  0.2153537

I think the faces should be planar but on the actual paper model i coudnt align them.

Any ideas what i did wrong ? 

Taff do you have the measuremets for a class II hex dome like the second pic ? (maybe with a level base ?)

[mike wazowski]

Good question Radu, i cheched the GP(2,2) that Gerry calculated and on acidome they have very diferent numbers.

I'm new to all of this so i dont really know what descried around or inscribed in means.

The incribed around V2 Class I looks like the GP (2,2) and the descried around V4 Class II looks similar but some edges are very small.

[Gerry in Quebec]

Hi Mike,

The chord factors of the Goldberg I (2,2) structure we've been discussing are based on a reference radius of 1.0 for the 20 vertices in the dome's footprint. Elsewhere in the dome some radii are also 1.0 but others are slightly less than that: either 0.99147 or 0.99185. As I may have mentioned in a previous post, this particular configuration has two distinct advantages for dome construction. First, the hemisphere sits flat: all 20 footprint vertices lie in the same equatorial plane with a theta coordinate of 90 degrees (the equivalent  0 degrees latitude in terrestrial cartography). Second, all the hexagons, half-hexagons and pentagons are perfectly flat. So this is a true polyhedron... all faces, including the floor, are planar.

If you were to try to build a Goldberg I (2,2) hex-pent dome by eliminating the "spokes" within the hexagons and pentagons of a class I, method 1, 6v icosa hemisphere, you would end up with a structure that sits flat at the equator, but the resulting hexagons would not be perfectly flat. And if you constructed the dome from the dual of a class II, 4v icosa geosphere using any of the widely known subdivision methods, you would end up with a dome whose hex and pent faces are all flat, but with an uneven base. For example, if the dual were based on method 1 of the 4v icosa, class II, the pathway formed by the 20 base struts would oscillate 1.00828 degrees above and below the true equator.

I tried to go to the acidome.ru website a few times, to see the feature Radu mentioned, but there was a navigation problem.

- Gerry

[mike wazowski]

I'm so lucky with you Gerry, otherwise i wouldnt know these things. 

Thanks again mate for clearing things up !

[mike wazowski]

Gerry you're measurements are perfect, you were right ! 

I'm almost finished with the second model (this time i did everything like you said) and it's looking just like it should !

Can i bother you with the GP(3,3) measurements ? 

Now that model will be a challenge !

[Gerry in Quebec]

Hi Mike,

 

I don't have a set of numbers for an I {3,3} Goldberg polyhedron that has a naturally flat base at a useful truncation when the zenith is a pentagon. As you can see in the attached diagram, this configuration, unlike the I {2,2}, doesn't split naturally into hemispheres. The imaginary equator runs between two edge pathways (red dashed lines). And, for this particular I {3,3} generated by Antiprism, those pathways zig-zag (green dashed lines).

As with the I {2,2}, there may exist an I {3,3} solution that gives you both planar hex faces AND a natural, clean truncation somewhere around the equator (e.g., 12/27, 13/27, 14/27, 15/27). However, I haven't done that exercise (it would be quite time consuming using my current tools).

One option is to make a 13/27 or a 15/27 dome, but move the base vertices into alignment to give a flat base (blue dashed lines). This involves some trig calculations and will add several edge lengths, which means you'd have several more face shapes to contend with. A second, much easier option is to follow Ken Brown's earlier suggestion and set the midpoint between pentagons as your dome zenith. Then you can split some hexes and pentagons down the middle to get an exact hemisphere with a flat base (second jpg attached). 

Let me know what you think and we can take it from there.

- Gerry in Québec

[mike wazowski]

Hi Gerry !

Purely form an estetic standpoint i would chose Option A 13/27, i know  Ken Brown's suggestion is much easier but it looks so 'ugly' with the 2 horizontal rows of hexagons.

Plus at least one dome from the Eden project has the Option A,  and that does look realy good.

Would it be easyer to make it even les then 13/27 ? 

Many many thanks for your help Gerry !!!

 

[Gerry in Quebec]

Hi Mike,

The Eden dome in the pic you posted appears to be a 12/27 truncation. I'll take a look at leveling the base for that option and get back to you. Meanwhile, if anyone else cares to dig out chord factors and angles for Mike, please do so. (Hint, hint.... Taff, Adrian?)

- Gerry

[Gerry in Quebec]

Hi Mike,
The edge lengths and face angles for the I {3,3} hex-pent dome, 12/27 truncation, are in the attached jpg. I used an Antiprism library file to generate the overall structure. It's probably not the same geometry as was used in the Eden Project dome.

I doctored the bottom row of hexes and partial hexes to produce a flat base, to have only two strut lengths in the base ring, and to make the floor radius constant for all 30 vertices.

How did your second run with I {2,2} turn out?
- Gerry

[mike wazowski]

Hi Gerry,

Holy smokes that looks complicated !

Man you are a genius, i wish i could know how you do all those calculation. 

Thank you so much !!!

I agree that the eden dome probably uses diferent measurements, and that's why it think yours will look better, i cant wait to make the model !

Will definetly let you know how it turns out.

[mike wazowski]

Hi Gerry,

I think you forgot 3 face angles : 

39-38-45

38-45-52

45-52-53

Thanks !

Best regards,

Mike

[Gerry in Quebec]

Hi Mike,

By symmetry:

39-38-45 = 10-9-14

38-45-52 = 9-10-15

45-52-53 = 10-15-19 Cheers, - Gerry

[Gerry in Quebec]

Mike,

Your I {2,2} turned out nicely. Crisper than mine.

Still trying to figure out where to store/display the model. Good humour in the household may begin to fray if I leave it too long on the dining room table. One advantage of making full spheres rather than domes is that they look nice when suspended from a workshop ceiling.

- Gerry

[mike wazowski]

Even if hex A is diferent from hex B ? 

Cause i need the angles for hex B

[mike wazowski]

And i thought your model looks better then mine :)

Gerry but that means that you'll have to make another dome to have the sphere :)) 

I have the same problem, where to put all of my dome models (4 in total atm)

[Gerry in Quebec]

The hexes you marked as A & B are identical, Mike. Look for the icosahedral symmetry.

Some other hexes and partial hexes (such as the gray ones along the base) are mirror images of each other. That means flipping some over before taping them together.

[mike wazowski]

Hi Garry,

Ofcourse you're right, sorry it was late last night. 

[Gerry in Quebec]

Mike and others,

Here's a bare-bones SketchUp model of the low-profile hex-pent dome discussed here: Icosa {3,3} Goldberg, with a level base at the 12/27 truncation. It's similar to one of the domes at the Eden Project in Cornwall, Southwest England.

- Gerry in Québec

[mike wazowski]

Thanks Gerry !

 

[Gerry in Quebec]

And for those who don't have SketchUp, here's a dynamic 3D pdf file. You can rotate the model, or zoom in and out, to get a more detailed view of the shape than a static jpg or png image would provide.

I exported the pdf from SketchUp using a plugin by SimLab Soft. You can use the plugin free for 30 days or for 30 file exports. Thereafter, it's something like $100 (ouch!).

Taff, thanks for bringing this plugin to our attention a few years back. I finally got around to trying it out!

- Gerry in Québec

[Gerry in Quebec]

This time with the pdf attached. (I need a wakeup coffee.)

- Gerry

[Adrian Rossiter]

Hi Gerry and All

On Wed, 10 Feb 2016, Gerry in Quebec wrote:

> And for those who don't have SketchUp, here's a dynamic 3D pdf file. You
> can rotate the model, or zoom in and out, to get a more detailed view of
> the shape than a static jpg or png image would provide.
>
> I exported the pdf from SketchUp using a plugin by SimLab Soft. You can use
> the plugin free for 30 days or for 30 file exports. Thereafter, it's
> something like $100 (ouch!).

I came across Sketchfab recently. It is an easy means of allowing
others to view models in 3D. There is a plugin to export from
Sketchup (I haven't used it)

https://sketchfab.com/exporters/sketchup

Sketchlab also works with Antiprism VRML output. This can be uploaded
as-is, but the default settings make the models look a bit dark and drab.

I don't think I would use Sketchlab for permanent content (I am
wary of this kind of service changing terms of use or disappearing),
but it is handy as a way of providing a temporary view of model,
accessible by simply clicking on a link in a message. e.g.

https://skfb.ly/Kpur

Adrian.
--
Adrian Rossiter
adr...@antiprism.com
http://antiprism.com/adrian

[Gerry in Quebec]

Thanks, Adrian. I'm checking into this. Seems like a practical solution, especially given the high cost of the SimLab Soft pdf plugin.

- Gerry

On Wednesday, February 10, 2016 at 6:08:25 AM UTC-5, Adrian Rossiter wrote:

Hi Gerry and All

[Gerry in Quebec]

Adrian & others,

I set up a SketchFab account and exported my first model directly from SketchUp using the free plugin.

Here's the link to the Goldberg I {3,3} hemisphere:

https://skfb.ly/KRTF

The wireframe display option doesn't seem to work on this model.

I'll also try out some wrl files via Antiprism.

- Gerry

[Adrian Rossiter]

Hi Gerry

On Thu, 11 Feb 2016, Gerry in Quebec wrote:
> I set up a SketchFab account and exported my first model directly
> from SketchUp using the free plugin.
>
> Here's the link to the Goldberg I {3,3} hemisphere:
>
> https://skfb.ly/KRTF

Looks fine. I was interested to see that the model got a Sketchfab
background. The Antiprism VRML specifies a background, but Sketchfab
ignores it and sets its own instead.

[Gerry in Quebec]

Here are two more 3D models:

 

4v icosa double-frame dome, 7/12 truncation, built as a 50-ft home in Vermont in 2013:

https://skfb.ly/KT9U

 

Icosa cap, 5 triangular frames using Oregon Dome's construction method (beveling the wide faces of 2x4s):

https://skfb.ly/KS8F

 

Any feedback on how easy or hard it is to view, manipulate and/or download such models would be welcome.

 

* * *

Adrian,

To edit a model's display settings in SketchFab, go to your collection of images and move your mouse cursor to the top right of the image you want to edit. A drop-down menu appears, with 7 choices including "3D settings". One of the choices is "Fixed background?". You can turn this on or off and select a fixed background. But you have to have the Pro version of SketchFab to upload your own custom backgrounds.

Overall, I like SketchFab, but navigation is quirky and the organization of various actions/functions/features doesn't always seem logical.

 

- Gerry

[Adrian Rossiter]

Hi Gerry

On Fri, 12 Feb 2016, Gerry in Quebec wrote:
> To edit a model's display settings in SketchFab, go to your collection of
> images and move your mouse cursor to the top right of the image you want to
> edit. A drop-down menu appears, with 7 choices including "3D settings". One
> of the choices is "Fixed background?". You can turn this on or off and
> select a fixed background. But you have to have the Pro version of
> SketchFab to upload your own custom backgrounds.

Thanks for the information, but that is the problem.

I uploaded around 60 files, where the file specified the background
and the camera. In every case Sketchfab added its own background
and applied its own camera settings, and I had to go into 3D settings
to remove the background and get a better initial viewing angle. It
was a bit tedious! I would rather just upload a file and it looks
the way it was intended to look.

I can live with it for occasional models, but I won't be doing
any more bulk uploads.

[Adrian Rossiter]

Hi Gerry

On Fri, 12 Feb 2016, Gerry in Quebec wrote:
> 4v icosa double-frame dome, 7/12 truncation, built as a 50-ft home in
> Vermont in 2013:
>
> https://skfb.ly/KT9U
>
> Icosa cap, 5 triangular frames using Oregon Dome's construction method
> (beveling the wide faces of 2x4s):
>
> https://skfb.ly/KS8F
>
> Any feedback on how easy or hard it is to view, manipulate and/or download
> such models would be welcome.

I could view them fine. My computer is around 10 years old and I
estimate I am getting around 5 FPS with both models.

[Gerry in Quebec]

Hi Adrian and others,

Thanks for checking out the appearance of those models models, Adrian.

Here's another one -- à propos of the earlier discussion with Mike about Goldberg I {3,3}:

https://skfb.ly/LqAV

Description of the Sketchfab entry:

This polyhedron is similar to the outer grid of one of the Eden Project domes in Cornwall, UK. It was created using Antiprism’s pol_recip program (www.antiprism.com) which generates the duals of polyhedra. The starting point was a class II, 6v icosahedral geodesic sphere. Once the dual was created, it was truncated above the equator with the help of Excel. If you think of this polyhedron as representing a slice of Earth, then Costa Rica’s capital, San José, would lie a tad north of the truncation plane.

- Gerry in Québec

On Friday, February 12, 2016 at 11:23:31 AM UTC-5, Adrian Rossiter wrote:

Hi Gerry