Simpler Floret Design
TaffGoch
%20dual.png?part=0.1)
homespun
TaffGoch
homespun
----- Original Message -----From: TaffGoch
TaffGoch



TaffGoch
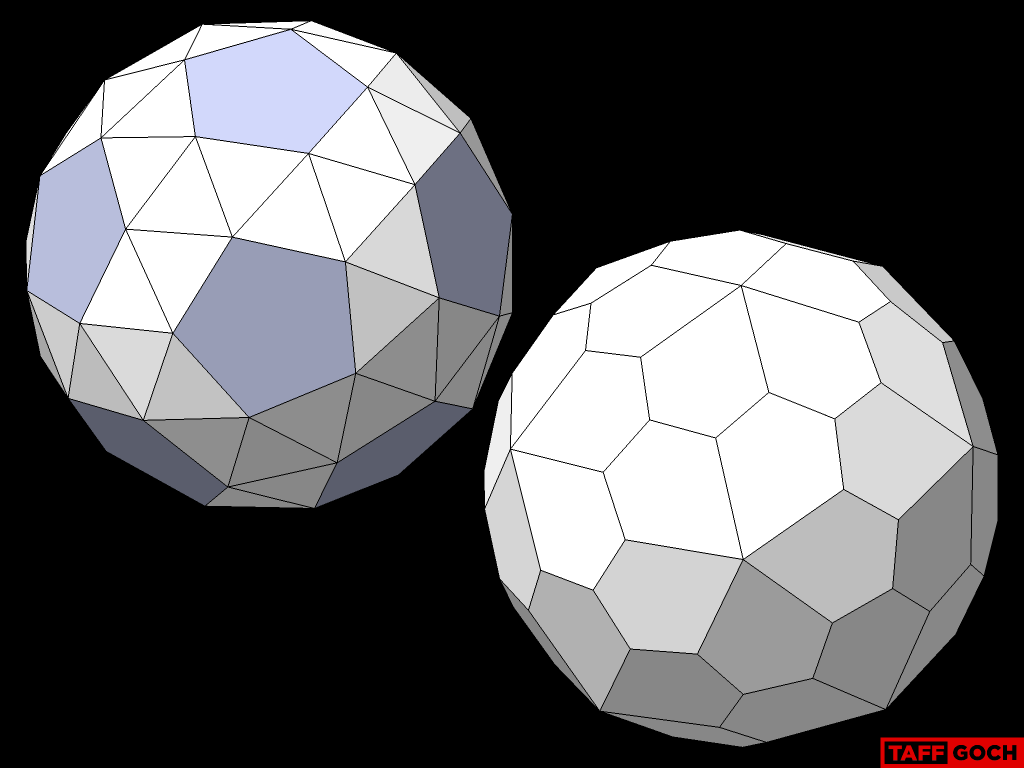
TaffGoch

TaffGoch
TaffGoch
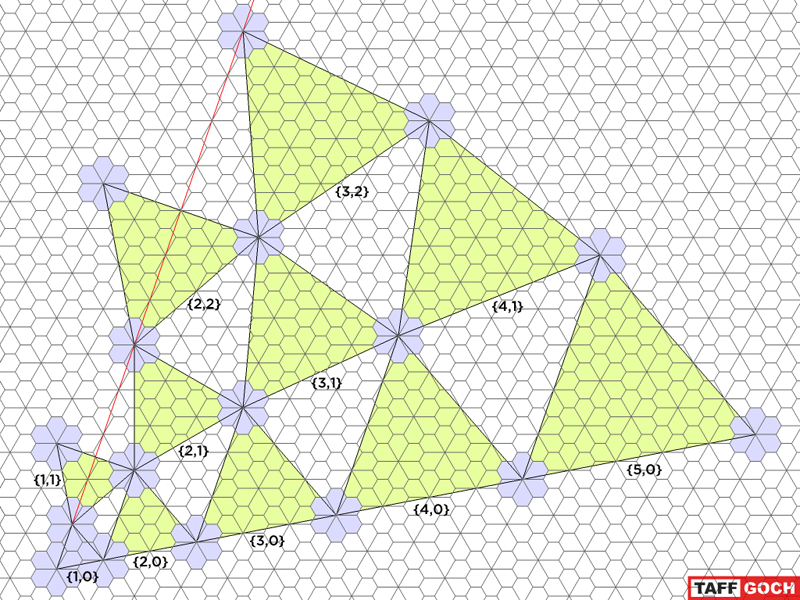

Dick Fischbeck
---Taff
TaffGoch
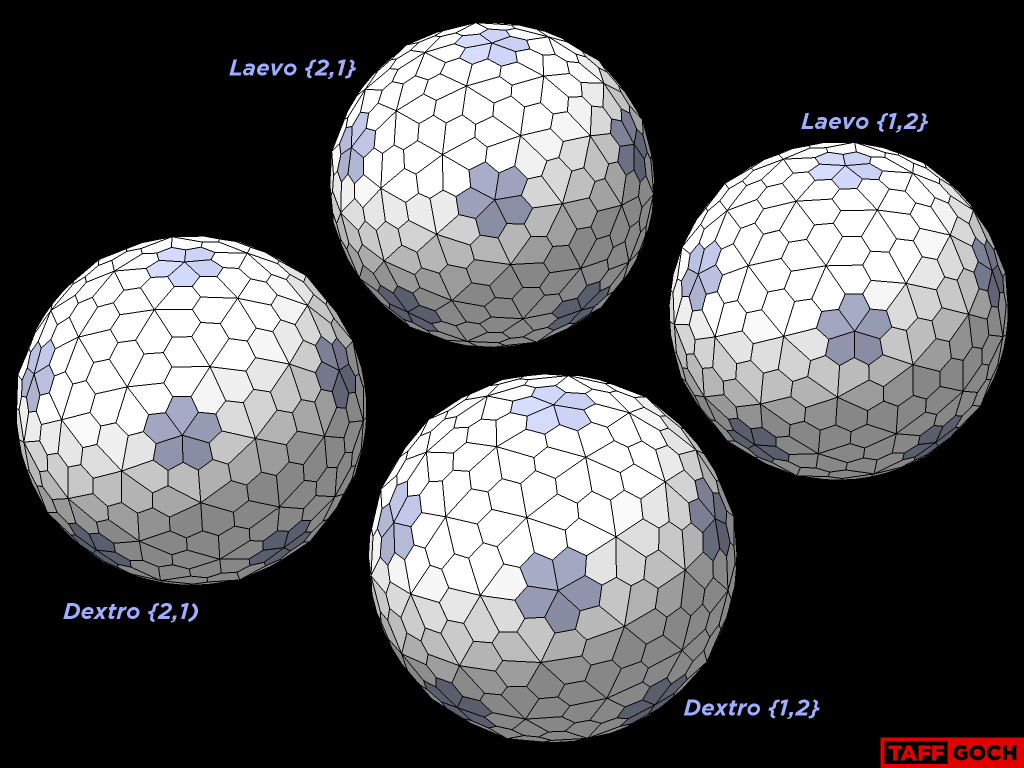
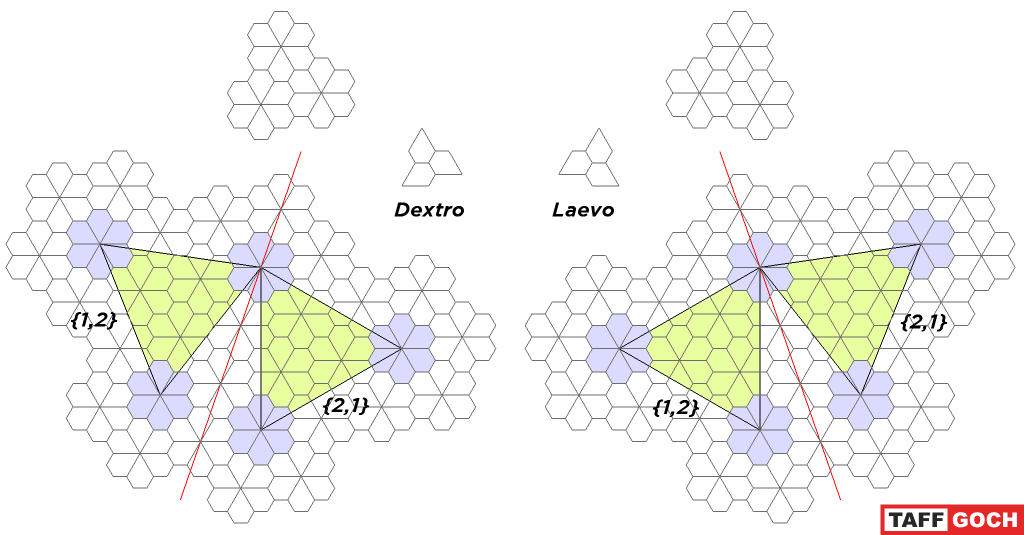
homespun
----- Original Message -----From: TaffGochSent: Monday, August 05, 2013 9:29 PMSubject: Re: Simpler Floret Design
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
For more options, visit https://groups.google.com/groups/opt_out.
TaffGoch
homespun
----- Original Message -----From: TaffGochSent: Monday, August 05, 2013 10:11 PMSubject: Re: Simpler Floret Design
Dan,Look through the different versions, and let me know which one(s) you want to construct. I'll make templates for those that you specify.-Taff
--
TaffGoch
TaffGoch
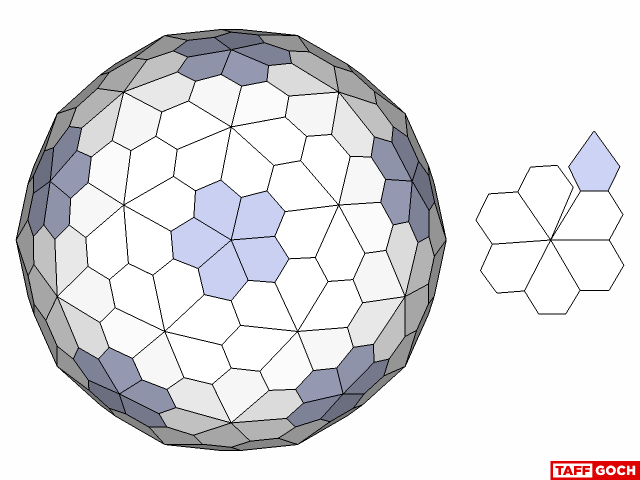
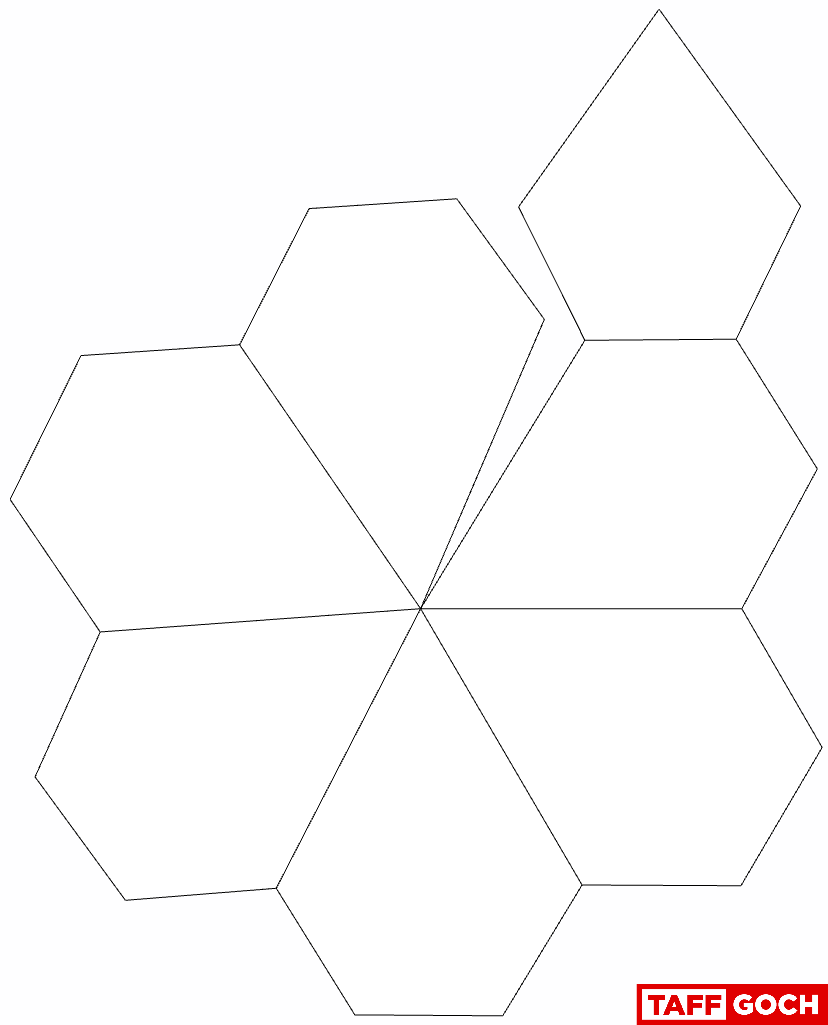
TaffGoch
Adrian Rossiter
On Fri, 2 Aug 2013, TaffGoch wrote:
> Interestingly, some arrangements can not be classified by Conway notation.
> I have used both, George Hart's online Conway notation javascript applet,
> and Adrian's "Conway" program, to generate cartesian coordinates. At least
> one, so far, required manual modeling of plane rotations and
> {3,1} example.)* If I'm wrong about this, I'd appreciate schooling from
to a general geodesic sphere.
In Antiprism, you can make the four "3,1" variations like this
conway g geo_1_3 | off_color -f S -m rng16 | antiview
conway rg geo_1_3 | off_color -f S -m rng16 | antiview
conway g geo_3_1 | off_color -f S -m rng16 | antiview
conway rg geo_3_1 | off_color -f S -m rng16 | antiview
Regarding your following post on the meaning of the numbers. I
don't define in Antiprism what it means to be 1,3 rather than
a 3,1 in geometric terms. The division is applied to a surface
made of oriented faces, and reorienting the faces flips the
pattern. E.g. a 1,3 pattern applied to a "positively" and
"negatively" oriented icosahedron produces models which are
mirrors of each other
off_util -O p ico | geodesic -c 1,3 | antiview
off_util -O n ico | geodesic -c 1,3 | antiview
Adrian.
--
Adrian Rossiter
adr...@antiprism.com
http://antiprism.com/adrian
Dick Fischbeck
TaffGoch
Adrian Rossiter
On Tue, 6 Aug 2013, TaffGoch wrote:
> My problem was that, as far as I can tell, "1,3" or "3,1" is not supported
> appreciated, by the way.)*
> So, is it correct to assert that one can not produce a 1,3 tessellation,
> using strictly "native" Conway notation?
produce a 3,1 geodesic icosahedron.
To prove this, notice that all the operations multiply the number
of edges by a factor from the range 1-6
http://en.wikipedia.org/wiki/Conway_polyhedron_notation#Operations_on_polyhedra
A 3,1 icosahedron has 390 edges, which has 13 as a prime factor.
This factor could not be introduced by operations so it must
have been a factor of the number of edges of the seed. The only
possibilities are Y, A or P with at least a 13-fold axis, but as
the geodesic icosahedron does not have an axis greater than 5-fold
these are discounted.
More generally there is freedom to choose the seed, hence I
started with a 3,1 geodesic icosahedron. The set of operations
may also been extended ("reflect" is an example), but the
geodesic pattern operation doesn't really fit into Conway Notation
operation, because it requires the tiling to be all triangles. A
tringulation operation could be incorporated, but that would be
messy as there would no longer be good formulas for the resulting
number of faces, edges and vertices.
TaffGoch
TaffGoch
TaffGoch
.jpg?part=0.4)
.jpg?part=0.2)
.jpg?part=0.1)
homespun
----- Original Message -----From: TaffGochSent: Sunday, August 25, 2013 5:56 PMSubject: Re: Simpler Floret Design
--
Camilla Fox
TaffGoch
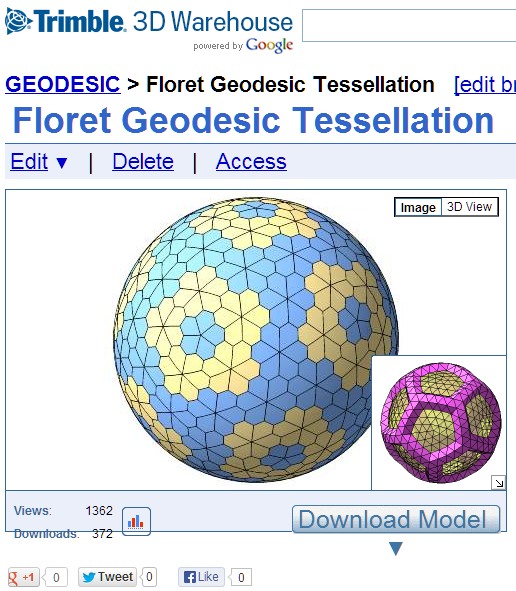
homespun
----- Original Message -----From: TaffGochSent: Monday, August 26, 2013 9:26 PMSubject: Re: Simpler Floret Design
Dan,Immediately, upon seeing this photo, thought of your octet constructs....
homespun
----- Original Message -----From: TaffGochSent: Monday, August 26, 2013 6:17 PMSubject: Re: Simpler Floret Design
.........Your cardstock model demonstrates that thin material, relative to the size of the model, is an unwise choice (but you're now wiser for the experience, eh?) As I'm sure you've noted from origami, a paper or card, folded sharply, is stronger than a shallow-folded example. Mechanically, this property scales-up, to real-world examples.............
TaffGoch
TaffGoch


homespun
----- Original Message -----From: TaffGochSent: Friday, August 30, 2013 3:26 PMSubject: Re: Simpler Floret Design
homespun


TaffGoch
homespun
----- Original Message -----From: TaffGoch
TaffGoch

TaffGoch
TaffGoch
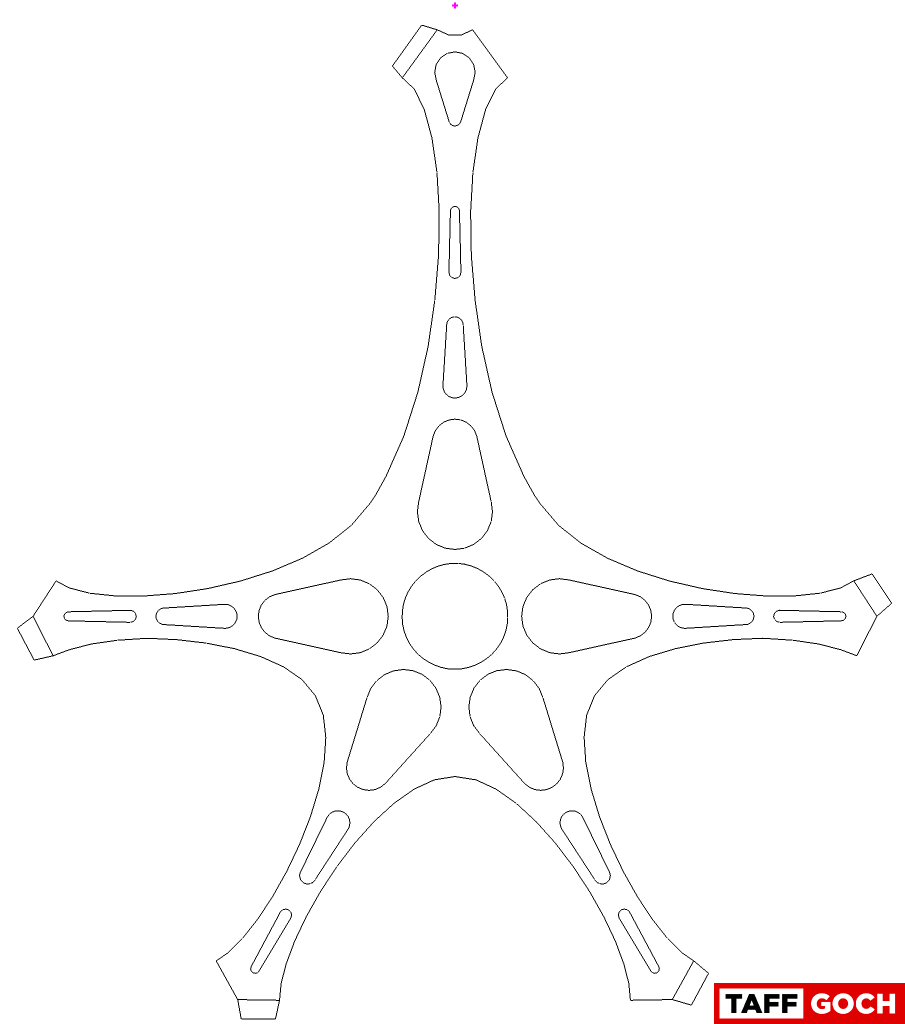
TaffGoch
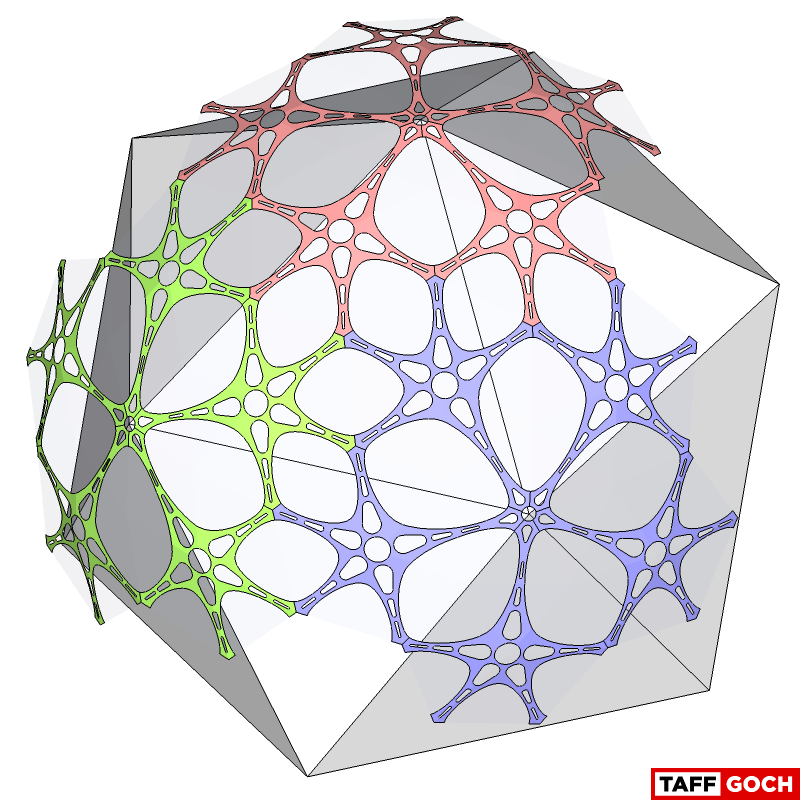
homespun
TaffGoch

homespun
----- Original Message -----From: TaffGochSent: Monday, September 02, 2013 5:00 PMSubject: Re: Simpler Floret Design - Pentagonal hexecontehedron
--
JRal
homespun
----- Original Message -----From: JRalSent: Tuesday, September 03, 2013 7:52 PMSubject: Re: Simpler Floret Design - Pentagonal hexecontehedron
TaffGoch
TaffGoch



John Ralphs
With the help of Taffs wonderful library of models in the SketchUp 3D warehouse, I'm going to give something with a higher frequency a shot using the same construction method of overlapping and pinning all the vertices as used on this lampshade.
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to a topic in the Google Groups "Geodesic Help Group" group.
To unsubscribe from this topic, visit https://groups.google.com/d/topic/geodesichelp/aEo8GK93leQ/unsubscribe.
To unsubscribe from this group and all its topics, send an email to geodesichelp...@googlegroups.com.
TaffGoch

homespun
----- Original Message -----From: TaffGoch
Sent: Friday, September 06, 2013 10:12 PMSubject: Re: Simpler Floret Design - Pentagonal hexecontehedron
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
TaffGoch



homespun
----- Original Message -----From: TaffGochSent: Saturday, September 07, 2013 6:44 PMSubject: Re: Simpler Floret Design - Pentagonal hexecontehedron
John Ralphs
homespun
----- Original Message -----From: John Ralphs
Sent: Monday, September 09, 2013 6:50 AMSubject: Re: Simpler Floret Design - Pentagonal hexecontehedron
homespun
Well, I decided I had to see if I could make the model, or at least part of it, with the 3 modules and with 2 layers. I didn’t have an exact pattern for the size of the inner layer, how much smaller I should make it to get the proper curvature, and how far apart the layers should be, -- so it was all “guesswork”.
And then I discovered that I had made the main module, the brown one, one segment too short on its long arm, and so I had to extend it.
And here it is, or as much of it as I am going to do. It’s rather crude, but it works, sort of. Anyway, this is how I envisioned the model when I saw the first pictures of the plans for Amazon/Seattle.
Dan
P.S. The architects did not respond to my mesage and pictures....
TaffGoch
TaffGoch
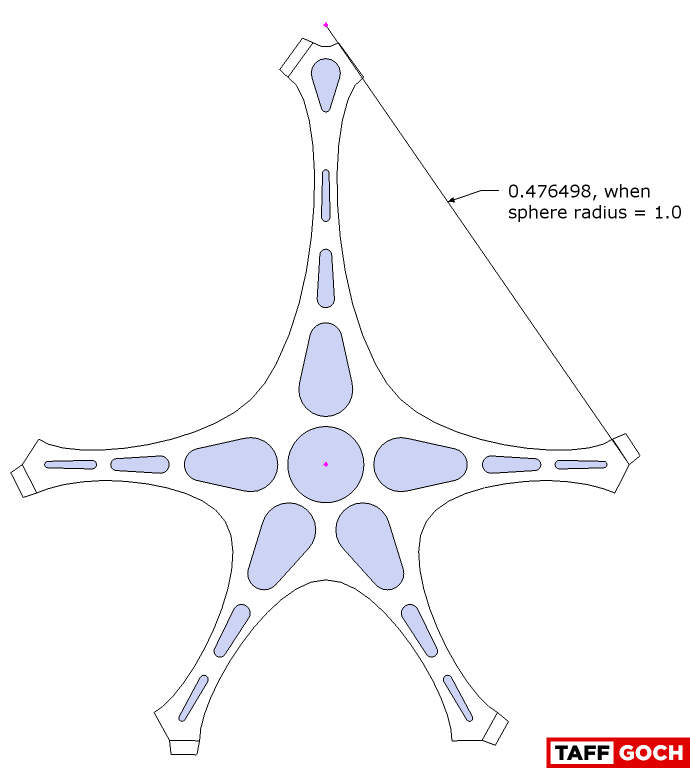
homespun
----- Original Message -----From: TaffGoch
Sent: Thursday, September 12, 2013 9:46 PMSubject: Re: Simpler Floret Design - Pentagonal hexecontehedron
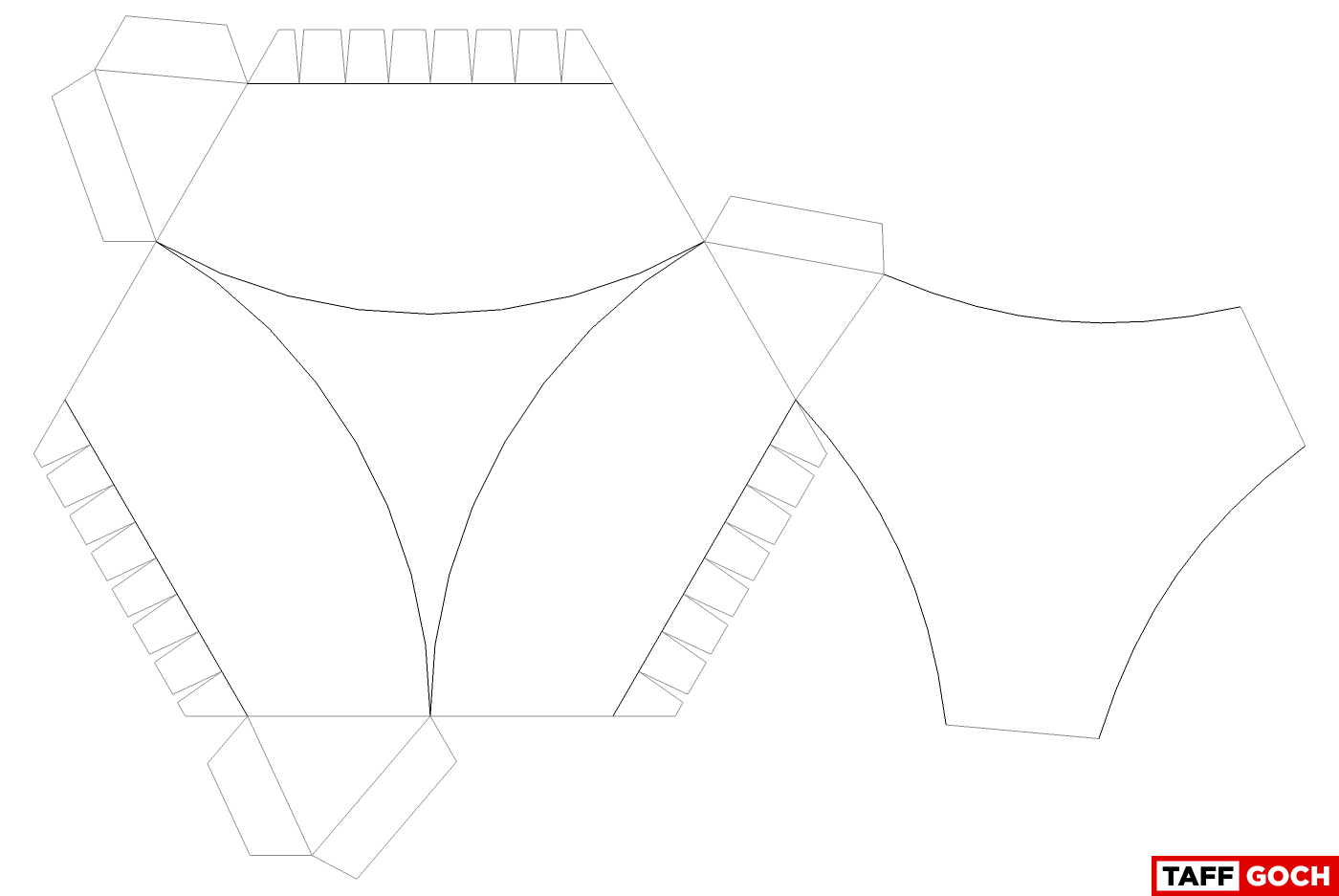
When you print the face pattern.......
David Reed
On Saturday, August 31, 2013 3:31:27 PM UTC-6, TaffGoch wrote:
Here's what I meant about it being "adjoined triangles"....
TaffGoch
David Reed
Adrian Rossiter
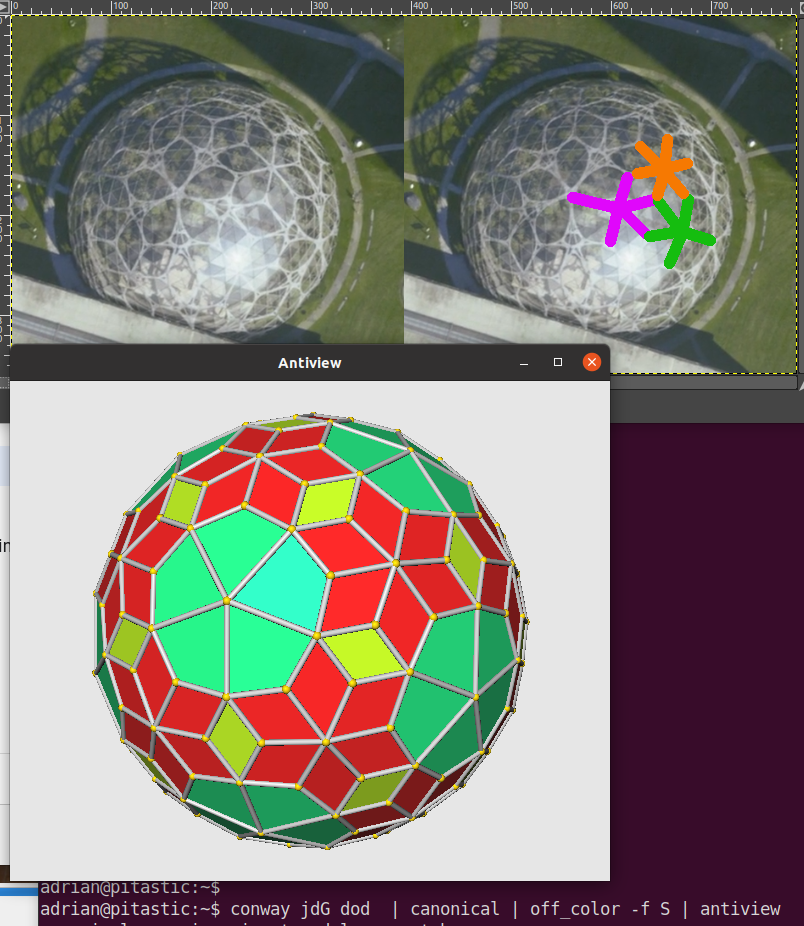
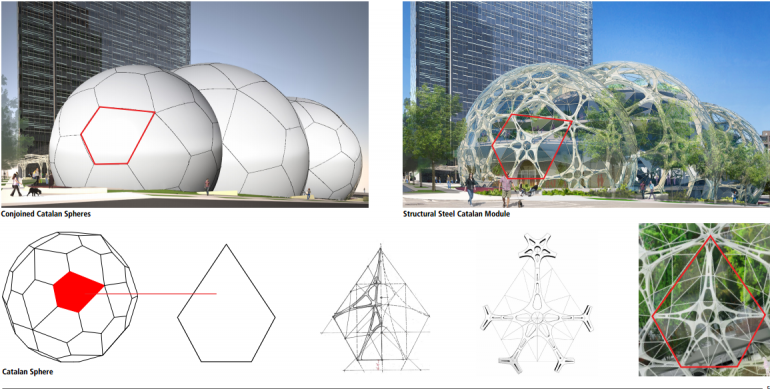
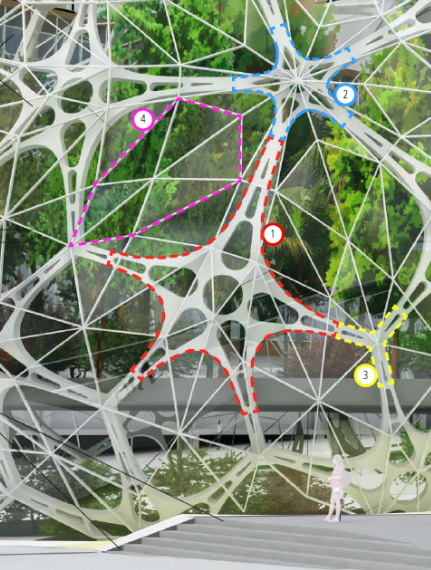
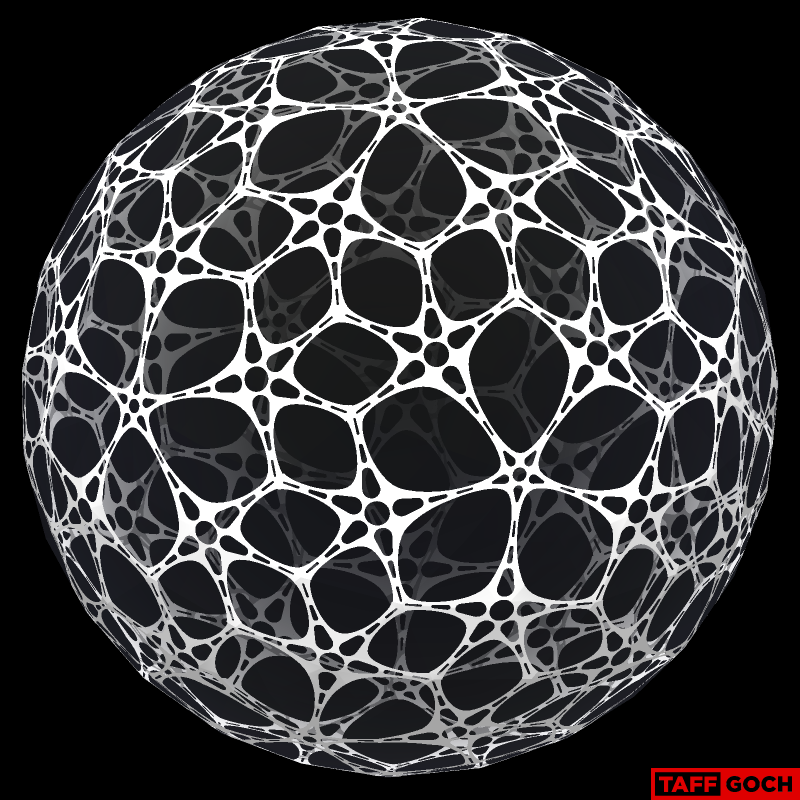
Another architectural geodesic floret tessellation (pentagonal hexecontahedron,) spotted online......being a proposed Amazon headquarters design, for Seattle:(Aug 20, 2013) http://www.gizmag.com/amazon-hq-update/28750/A previous (declined) proposal was not icosahedron-based:
uncledan homespun4homeschoolers.com
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/geodesichelp/89d1577b-ac5b-4588-b469-fa7810f1b395n%40googlegroups.com.
Adrian Rossiter
On Thu, 2 Jun 2022, uncledan homespun4homeschoolers.com wrote:
> I would like to build this model with paper. Are the red ones rhombi
> or are they kites? Can you tell me some realtive dimensions and angles
> to work from?
around the 3-fold axis are mirrored.
Display some face and vertex numbers
conway jdGD | canonical | off_color -f S | antiview -n vf
Face 62 is green, 63 red, and 64 yellow. Lets get angles and edge
lengths for these faces, to 8 significant digits
conway jdGD | canonical | off_color -f S | off_query -d 8 -I 62,63,64 Fal
62,128.48871 80.55429 70.402714 80.55429,0.2337192 0.36516585 0.36516585 0.2337192
63,65.445975 115.06652 58.852674 120.63483,0.2337192 0.25679988 0.24973596 0.22665528
64,117.63665 62.363351 117.63665 62.363351,0.22665528 0.22665528 0.22665528 0.22665528
This is the face number, followed by the angles, follwed by the length
of the edge following each of these angles
This is clear for the green (62) kites and the yellow (64) rhombi.
The red (63) faces are neither kites nor rhombi, and we don't know
where on the face the angle and edge report starts, nor in which
direction. Rather than infer it, we could add the vertex numbers to
the report for this face
conway jdGD | canonical | off_color -f S | off_query -d 8 -I 63 Fval
63,16 109 73 196,65.445975 115.06652 58.852674 120.63483,0.2337192 0.25679988 0.24973596 0.22665528
This says the first angle (65.445975) is at vertex 16, and the first
length (0.2337192) is between vertices 16 an 109. The next angle
(115.06652) is at vertex 109 and the next length (0.25679988) is
between vertices 109 and 75. Etc. These quadrilaterals come in
mirror pairs, so when assembling the model half will need to be
flipped over.
Adrian.
--
Adrian Rossiter
adr...@antiprism.com
http://antiprism.com/adrian
uncledan homespun4homeschoolers.com
----You received this message because you are subscribed to the "Geodesic Help" Google Group--To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com--To post to this group, send email to geodes...@googlegroups.com--For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/geodesichelp/alpine.DEB.2.22.394.2206021615580.345038%40pitastic.

.png?part=0.1)
.png?part=0.2)




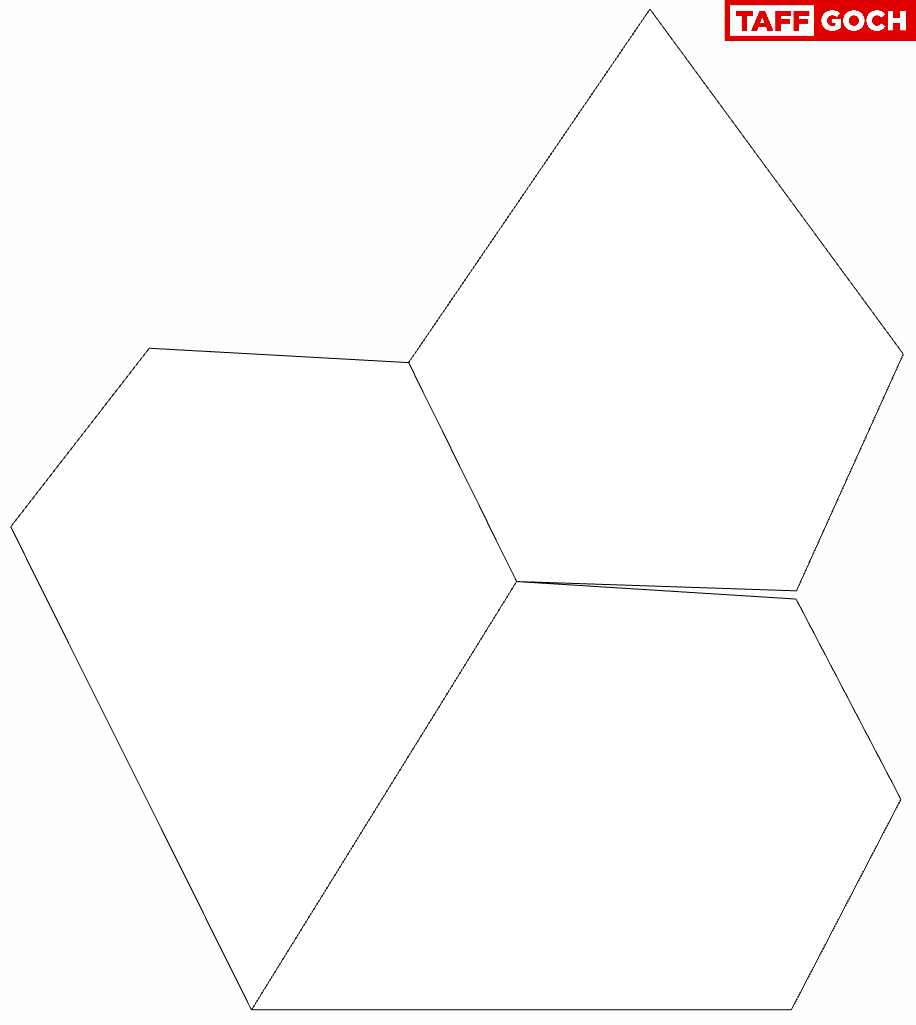


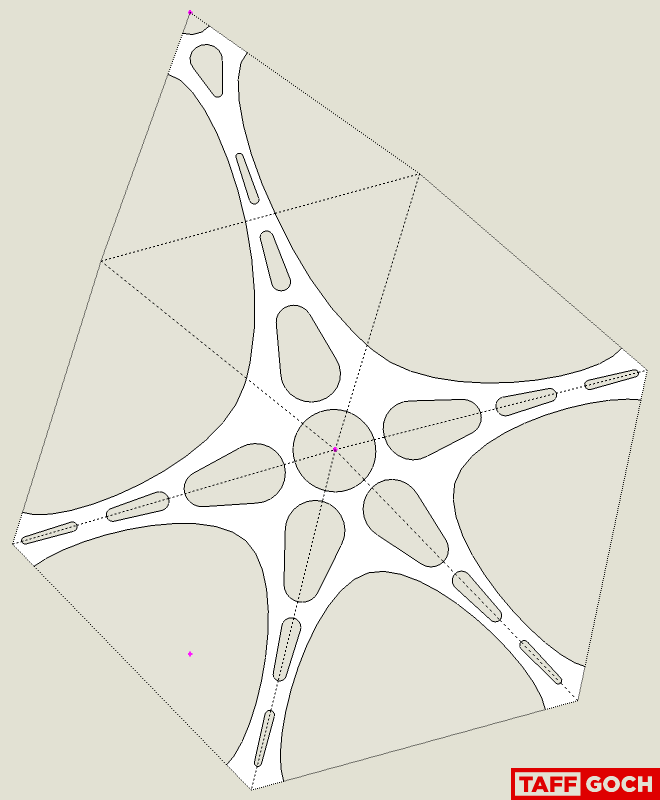




 Dan
Dan