New Nexorade/Rotegrity project
TaffGoch
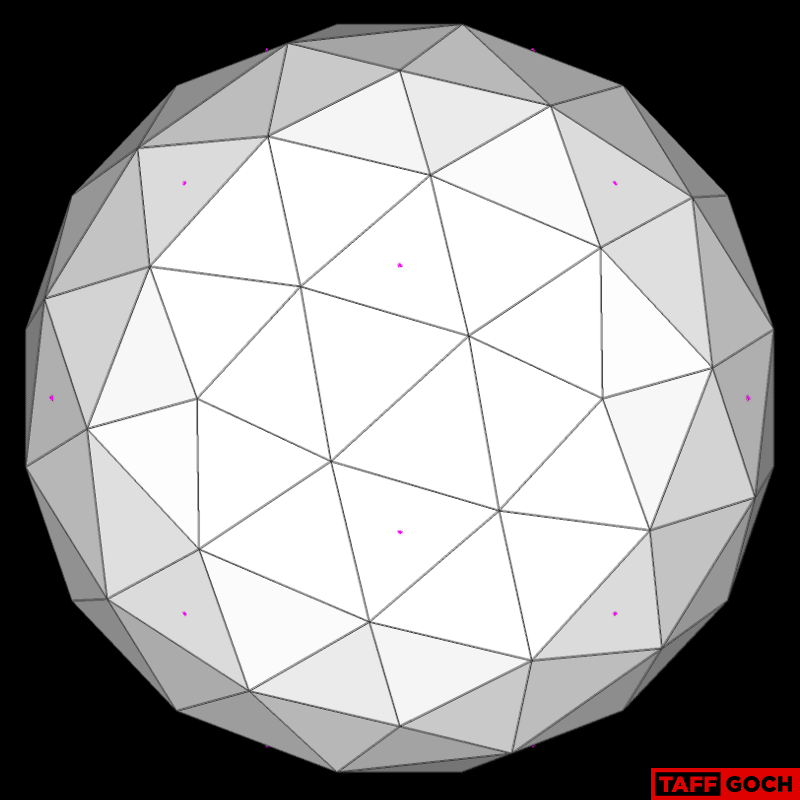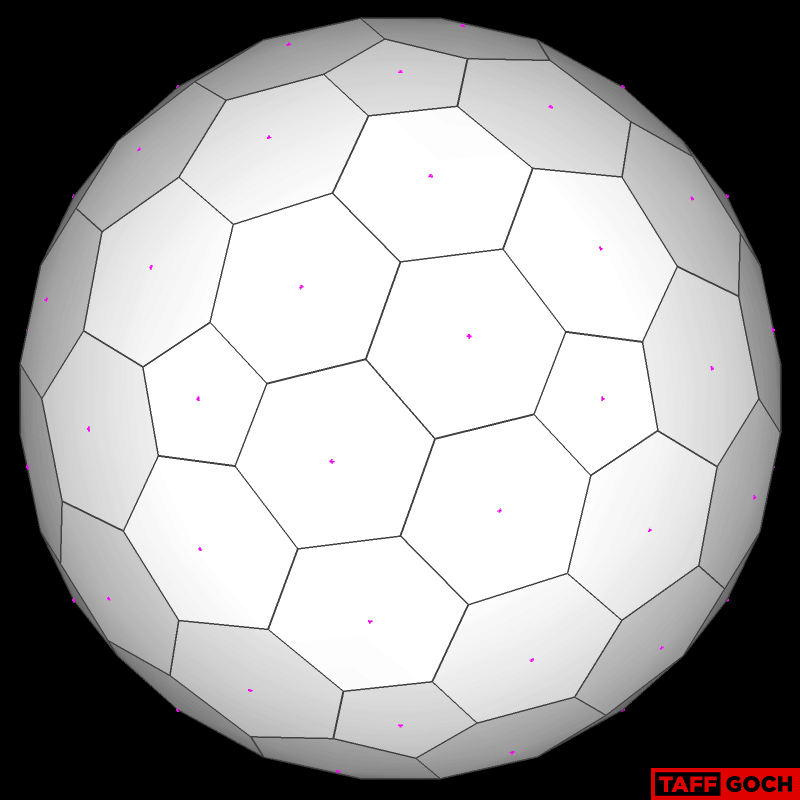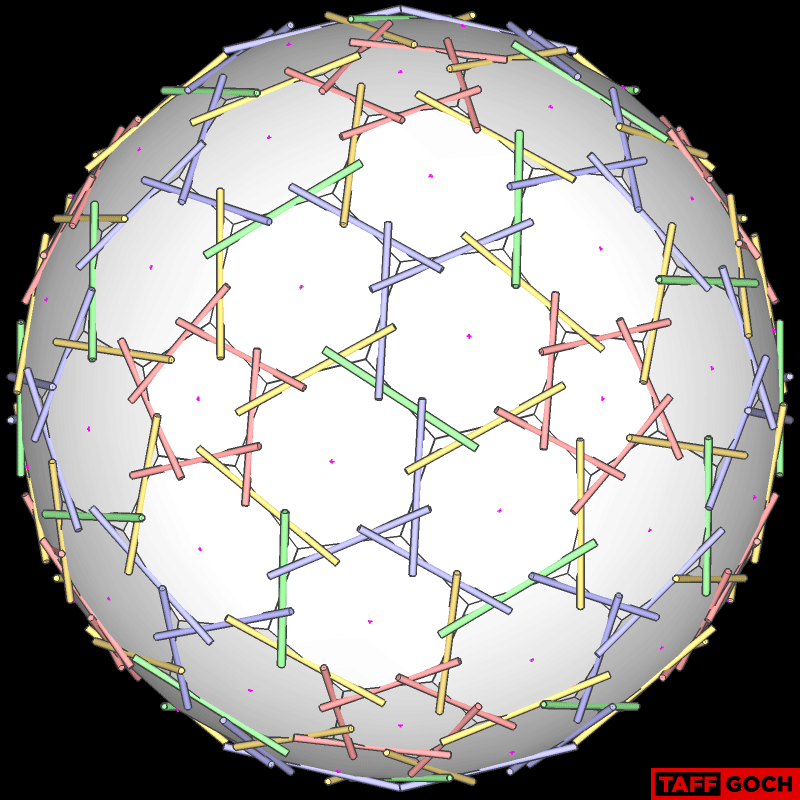
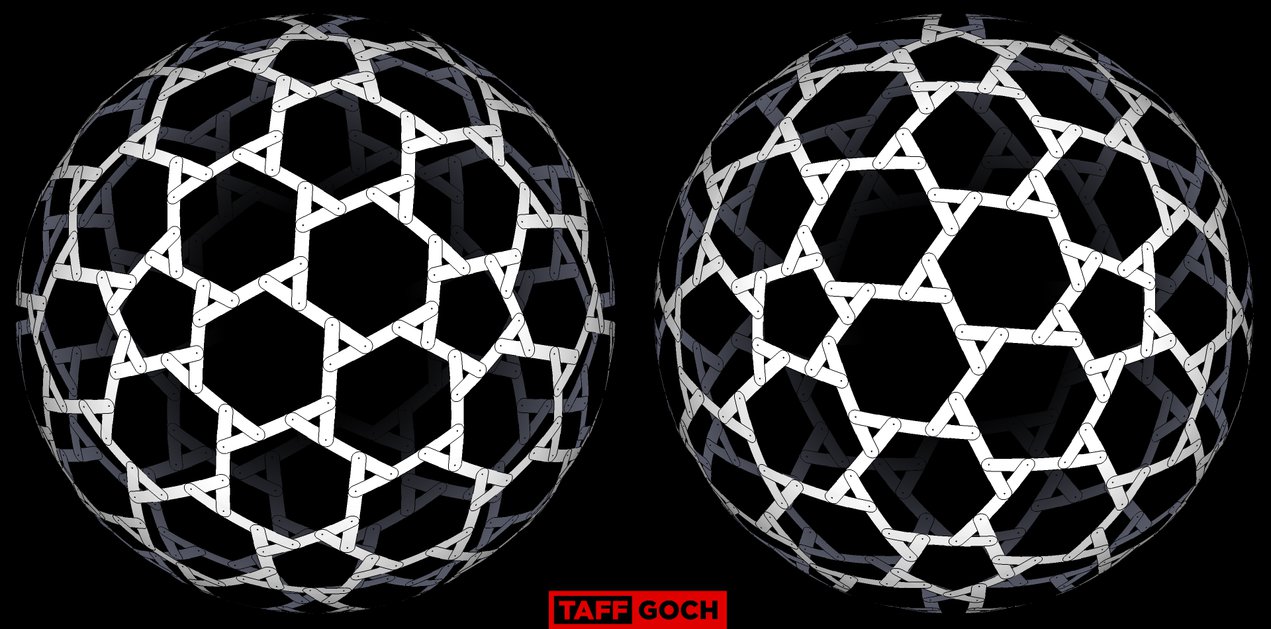

TaffGoch
TaffGoch

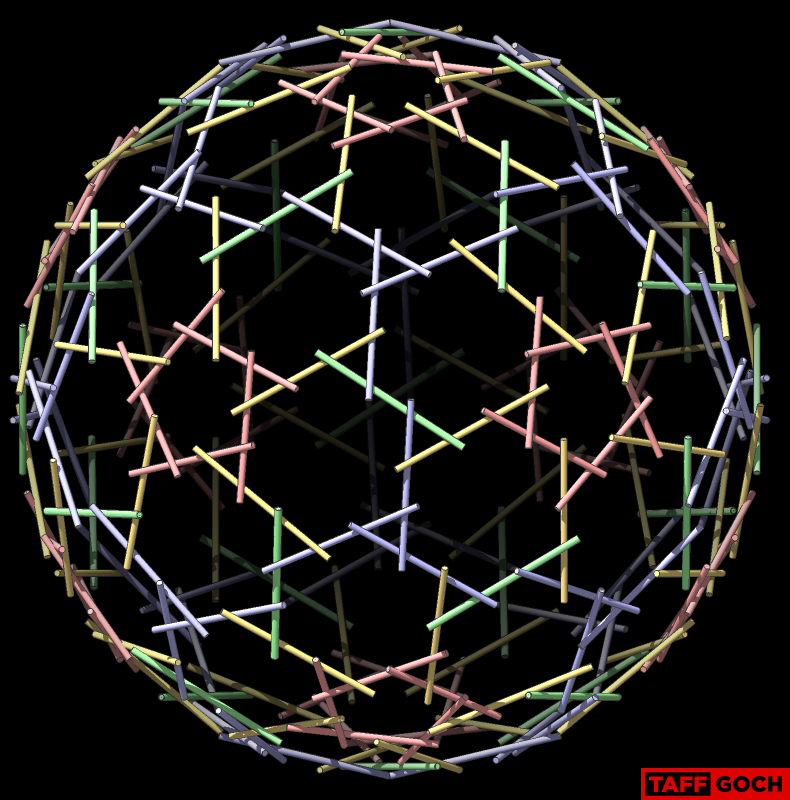



TaffGoch
Beautiful nexorade. Maybe you can cover it with heat-shrink boat plastic. Do you know if it is possible to have just one or two lengths of nexors?
TaffGoch
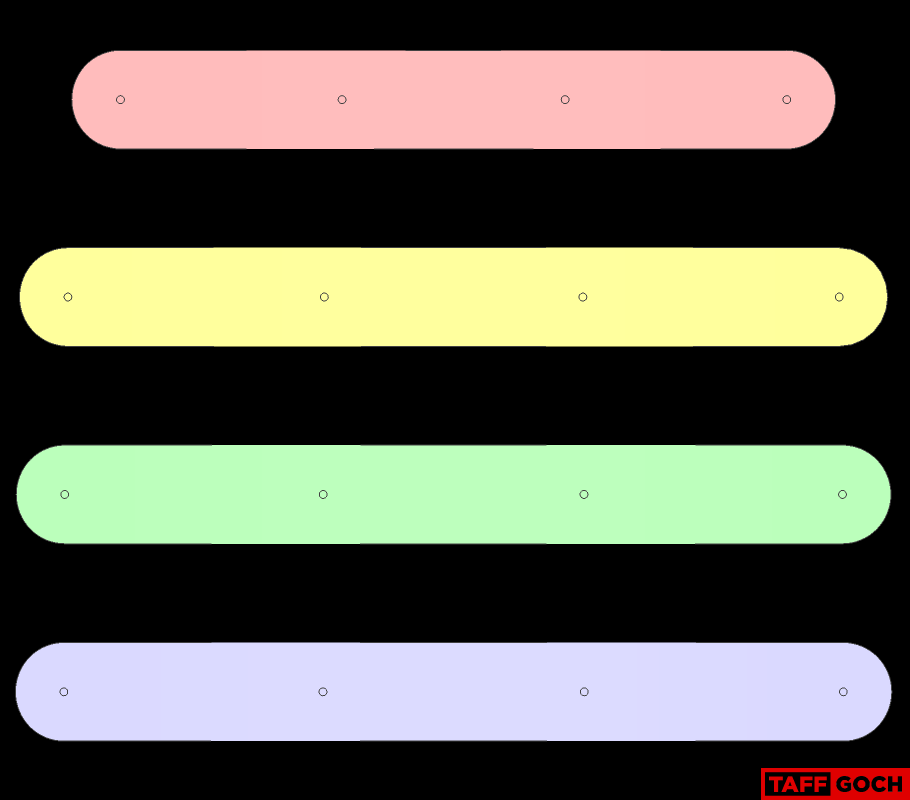
TaffGoch
TaffGoch
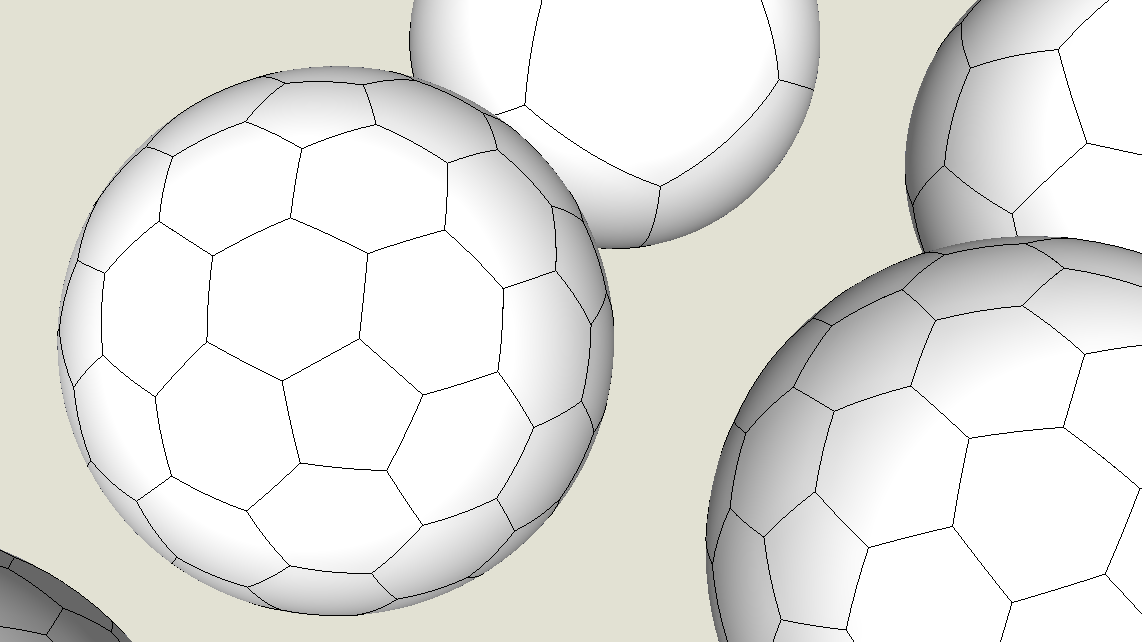
TaffGoch

TaffGoch
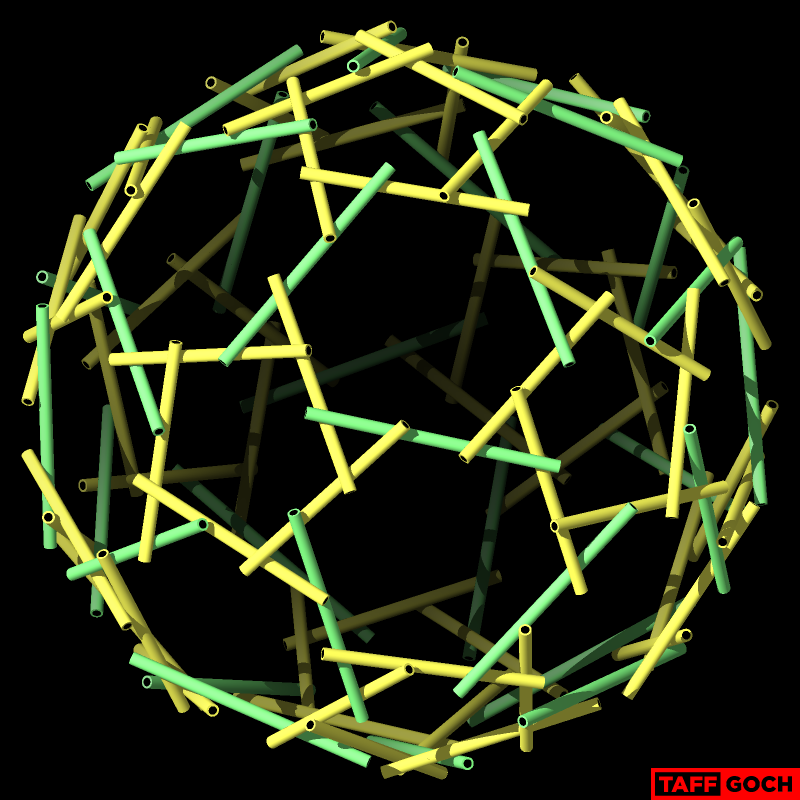
TaffGoch

TaffGoch
https://3dwarehouse.sketchup.com/model.html?id=5b5a1809-5e01-496b-b03d-060c82a72494
-Taff
(File attached, as well.)
TaffGoch

muhammad karim Toury
TaffGoch
I've completed the model, and will work on the bolt centerlines, next.
muhammad karim Toury
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp+unsubscribe@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to a topic in the Google Groups "Geodesic Help Group" group.
To unsubscribe from this topic, visit https://groups.google.com/d/topic/geodesichelp/RFBZ6uFmsjU/unsubscribe.
To unsubscribe from this group and all its topics, send an email to geodesichelp+unsubscribe@googlegroups.com.
For more options, visit https://groups.google.com/d/optout.
muhammad karim Toury
--
muhammad karim Toury
TaffGoch

muhammad karim Toury
--
TaffGoch
It varies, somewhat, for different tessellations. For example, this greater/lesser rotegrity pair...

TaffGoch
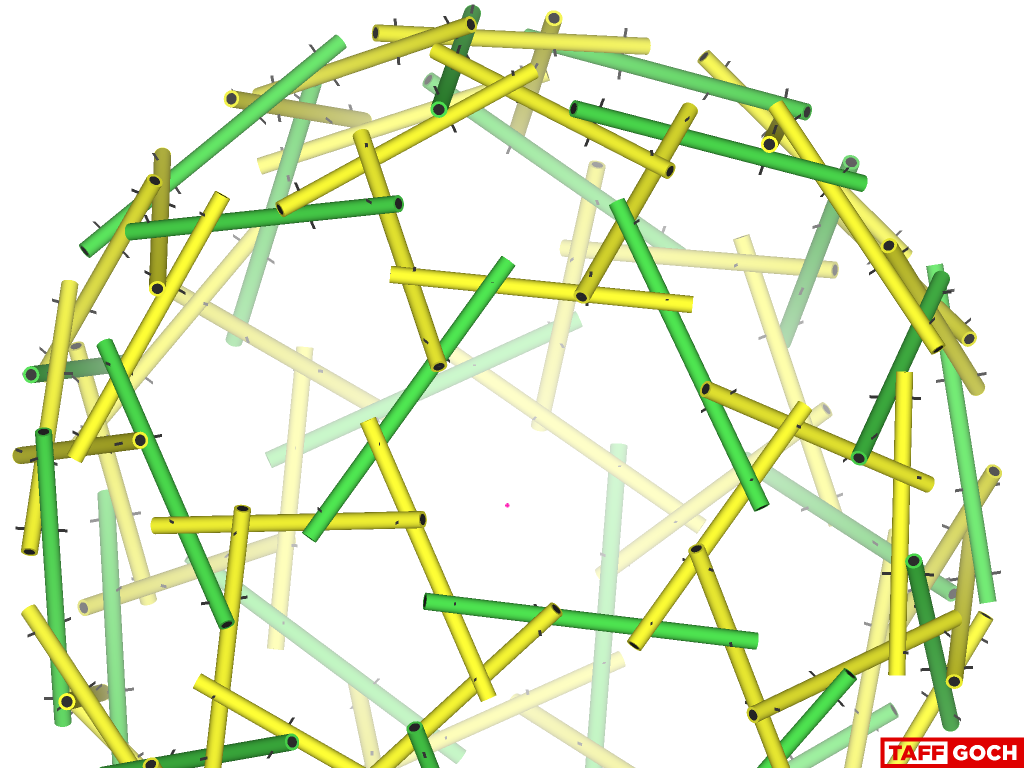
muhammad karim Toury
--
muhammad karim Toury
--
TaffGoch
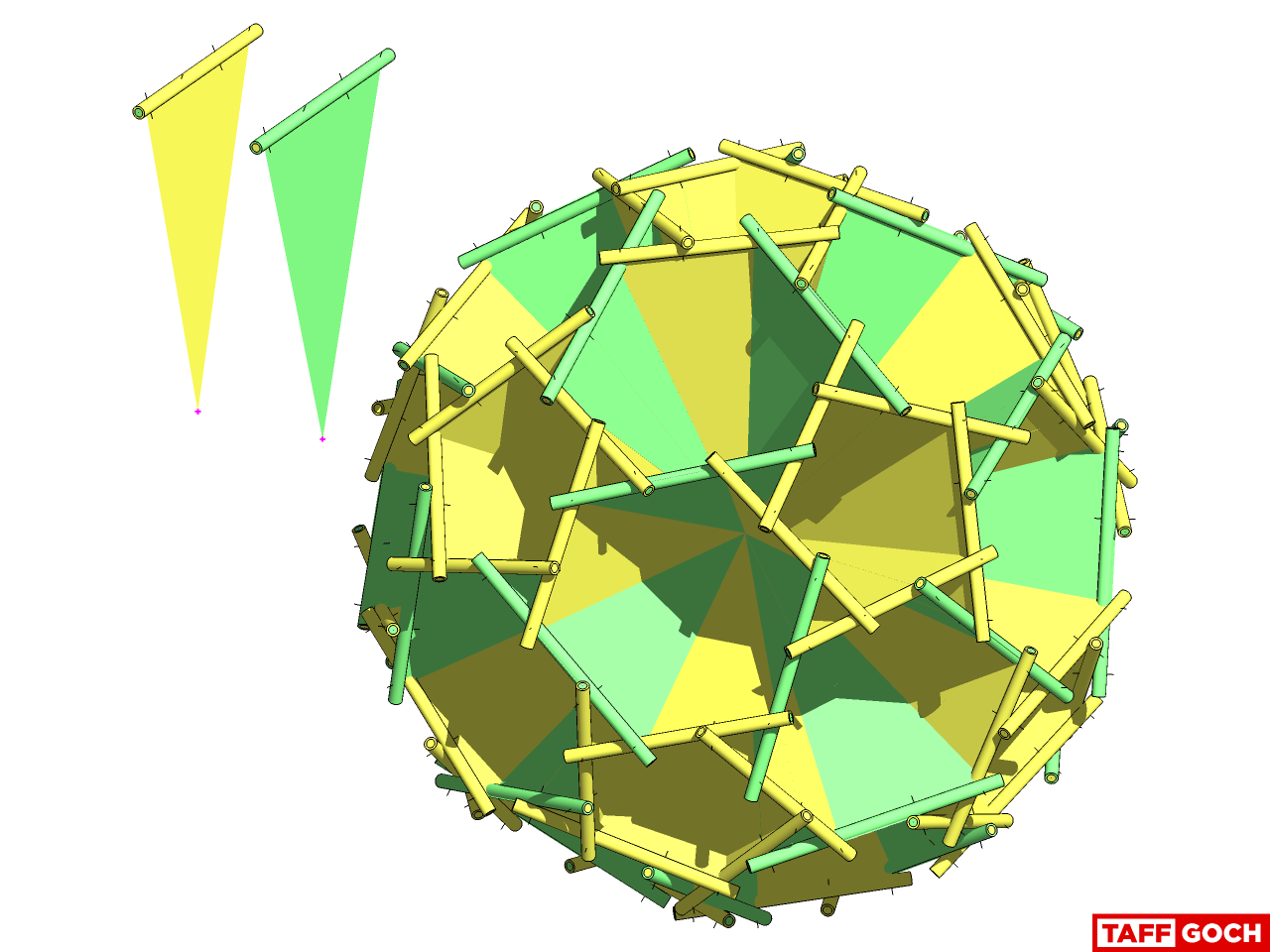
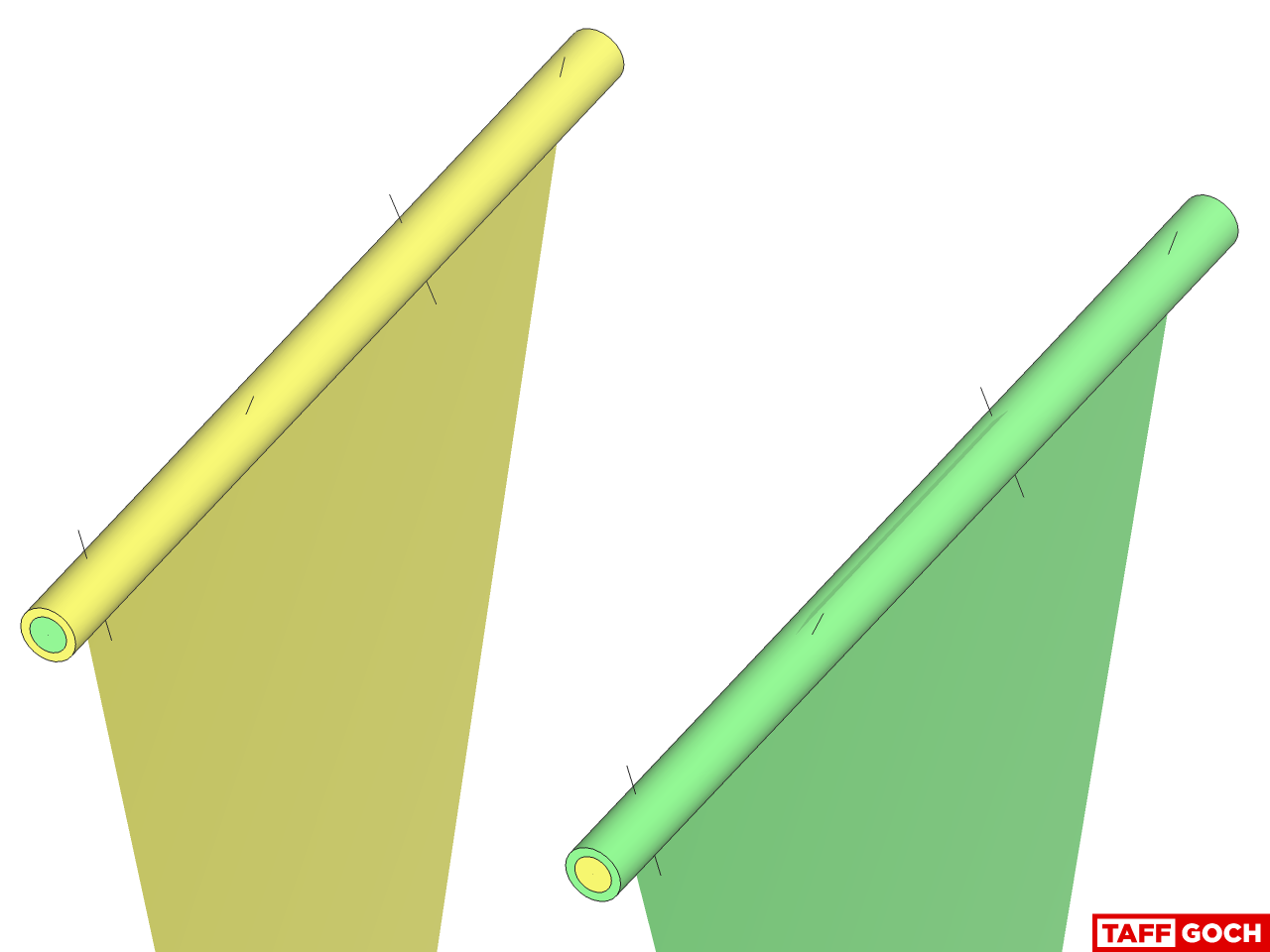
... the pent strut (yellow) CAN NOT! I have color-coded the end of the yellow strut, to depict which end is connected to the green strut. If you examine the top-most nexorade reference image, you will note that one end of the yellow strut is green, while the other end is yellow. (The green strut ends are both yellow.)
TaffGoch
https://groups.google.com/forum/#!topic/geodesichelp/vrDkGnHlX-Y
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
TaffGoch
https://www.google.com/search?as_epq=Kenneth+Snelson
muhammad karim Toury
--
TaffGoch
And because both ends of greens rest on yellows we can flip them end-over-end."
Your understanding of yellow/green strut orientation is correct
-Taff
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
muhammad karim Toury
Ashok Mathur
Ashok
muhammad karim Toury
TaffGoch
I have not provided you any rotegrity measurements or angles. I don't understand your queries.
___________________________
(I was "eyeballing" the end lengths, to relate to overhang. Since the angles between nexors are different on each end of a yellow nexor, I extended the end length at one end to provide roughly the same overhang.)
___________________________
muhammad karim Toury
I have not provided you any rotegrity measurements or angles. I don't understand your queries.
You said me that you call the different geometries lesser and greater,
Anyway, I bought plastic tubes to make a model in real scale and check the precision that I need before cut and drill the metals.
Muhammad
--
TaffGoch
muhammad karim Toury
--
TaffGoch
______________________________
TaffGoch
muhammad karim Toury
--
AzaFran
That's it, guys! More details please about align bolts-holes really interesting. I'm also studying to make a model and later a bigger structure learning about rotregrity. Thanks for share and keep'n good work.
Looks really nice,
Regards,
Taji
~~~~~~~~~~~~~~~~~
D.A.L.E!
Despertando a la Ekosofía
~~~~~~~~~~~~~~~~~
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp+unsubscribe@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
TaffGoch
now this is dismantled."
_________________
Dick Fischbeck
TaffGoch
Nexorade • 2v{1,1} • 3D Warehouse
TaffGoch









Dick Fischbeck
TaffGoch
The "pallet" dome (the subject of another posting,) was designed/constructed by the same folks that designed the the Spanish nexorade dome.
http://control-zeta.org/
Yaser Shahbazi
Yes. This Rotegrity has been made by Tabriz Islamic Art University - Architectural Technology Group in 4IASC congress that held in Shahid Beheshti University as one day Reciprocal Workshop.
The construction has started about 9 am and finished about 10 pm. There is a 3:47 TimeSlap that I attach for you in:
https://drive.google.com/open?id=0B0BbJ0fK36gwYllYZEFzWmhHTkk
homespun


biagiodicarlo
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
Ashok Mathur
Regards
Ashok
Ashok
Very nice, Dan! How are the connections made between the pieces?
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp+unsubscribe@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
TaffGoch
___________________
https://groups.google.com/d/msg/geodesichelp/RFBZ6uFmsjU/7dwOJJ8mBwAJ
You can always find them online, here, as well:
http://taffgoch.deviantart.com/art/Rotegrity-3v-1-2-625451741

http://taffgoch.deviantart.com/art/Nexorade-3v-2-1-Alternates-623335175

homespun
I printed the templates on paper and cut them out. Then I used glue stick to attach them to cereal box cardboard, and cut them out again. I used a pushpin to make the holes. Then to assemble I used pushpins and paper clips to temporarily hold a few straps in position. I would remove the paper clips and push pins one at a time and use a stapler to make the permanent attachments.
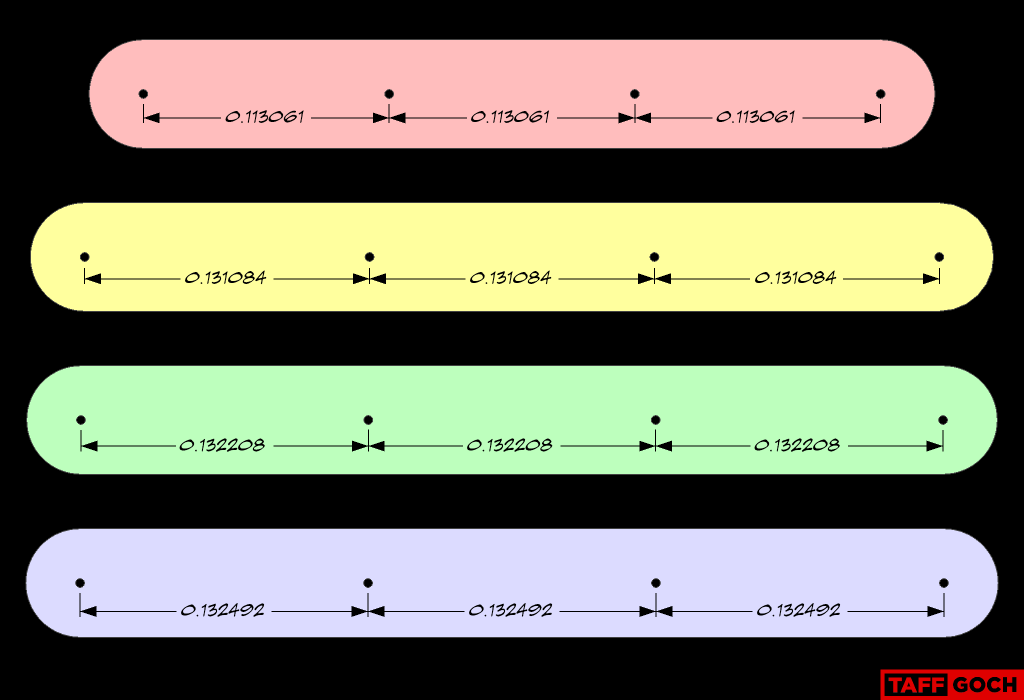
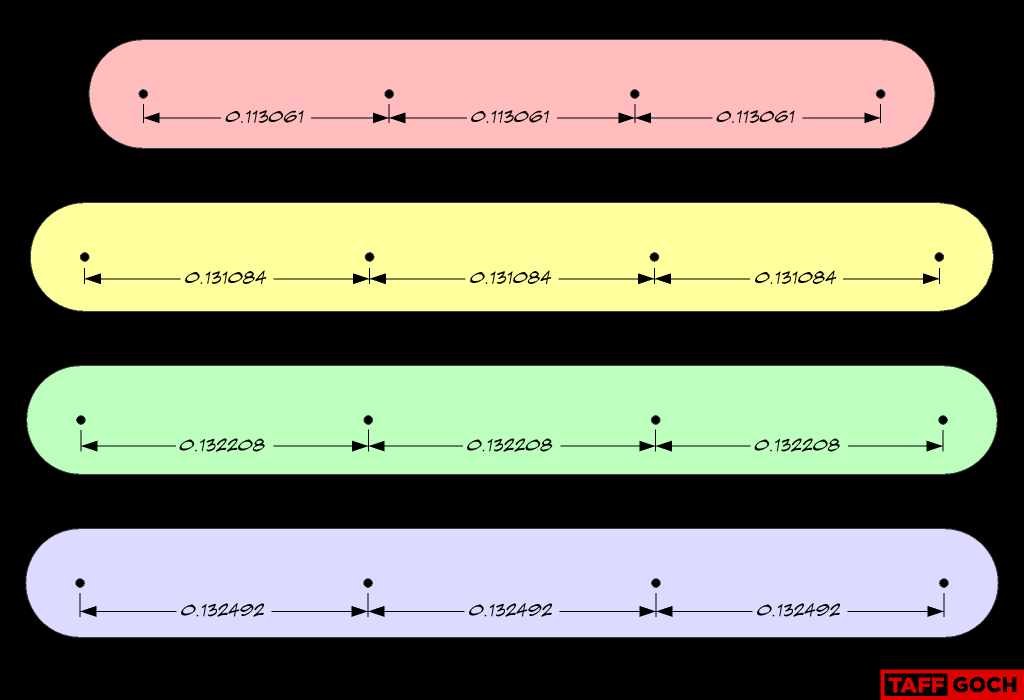
I used 60 short straps (0.113061), and I think it was 150 long straps all of the same size (0.132208).
Just give it a little push and it rotates so nicely. FUN! See 12-second video: http://tinyurl.com/hov7r67
Dan
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
Ashok Mathur
Ashok
To unsubscribe from this group, send email to GeodesicHelp+unsubscribe@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp+unsubscribe@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
homespun

--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
Ashok Mathur
Ashok
TaffGoch
TaffGoch
You have to allow for some (minor) rotation, during initial joint connection. After multiple adjacent initial connections have been made, the need for rotational allowance is no longer needed. Final connections can then be "made" rigid.
Ashok Mathur
Ashok
Ashok
--
TaffGoch


homespun


--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
Olga
Ashok Mathur
Ashok
--
TaffGoch
.png?part=0.1&view=1)

homespun
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
TaffGoch
A rotegrity is a nexorade, but a nexorade isn't necessarily a rotegrity (but can be.)
At least that's been my experience; how I've read/heard the terms bandied about,
homespun
Olga
Do you have experience in using of struts of the same length for 3V dome?
Regards
Ashok
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.
Olga
I want to build a quarter of the sphere, as terrasse roofing. I will fix them with screws, becouse for the winter i have to move it away.
Blair Wolfram
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp+unsubscribe@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
For more options, visit https://groups.google.com/d/optout.
Olga
Ashok Mathur
Ashok
To unsubscribe from this group, send email to GeodesicHelp+unsubscribe@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp+unsubscribe@googlegroups.com.
Olga
Arnd Marijnissen
On Friday, August 4, 2017 at 2:54:33 PM UTC+2, Blair Wolfram wrote:
I'd like to see this.Do you have pictures?On Fri, Aug 4, 2017 at 5:02 AM, Olga <olg...@gmail.com> wrote:Dear Taff,i have struts, which are a little bit curved. I use old bed sluts. I sown them to double the amount.they are also a Little flexible.
I want to build a quarter of the sphere, as terrasse roofing. I will fix them with screws, becouse for the winter i have to move it away.
--
Justa
Olga
Hello all,
TaffGoch
Based on your prior post...
"I want to build 3v, 2.1, but have only 80 cm long struits, approx.120 - 140 pieces..."
...and your photo, I've started on a 3D model:

Olga
Nathaniel Virgo
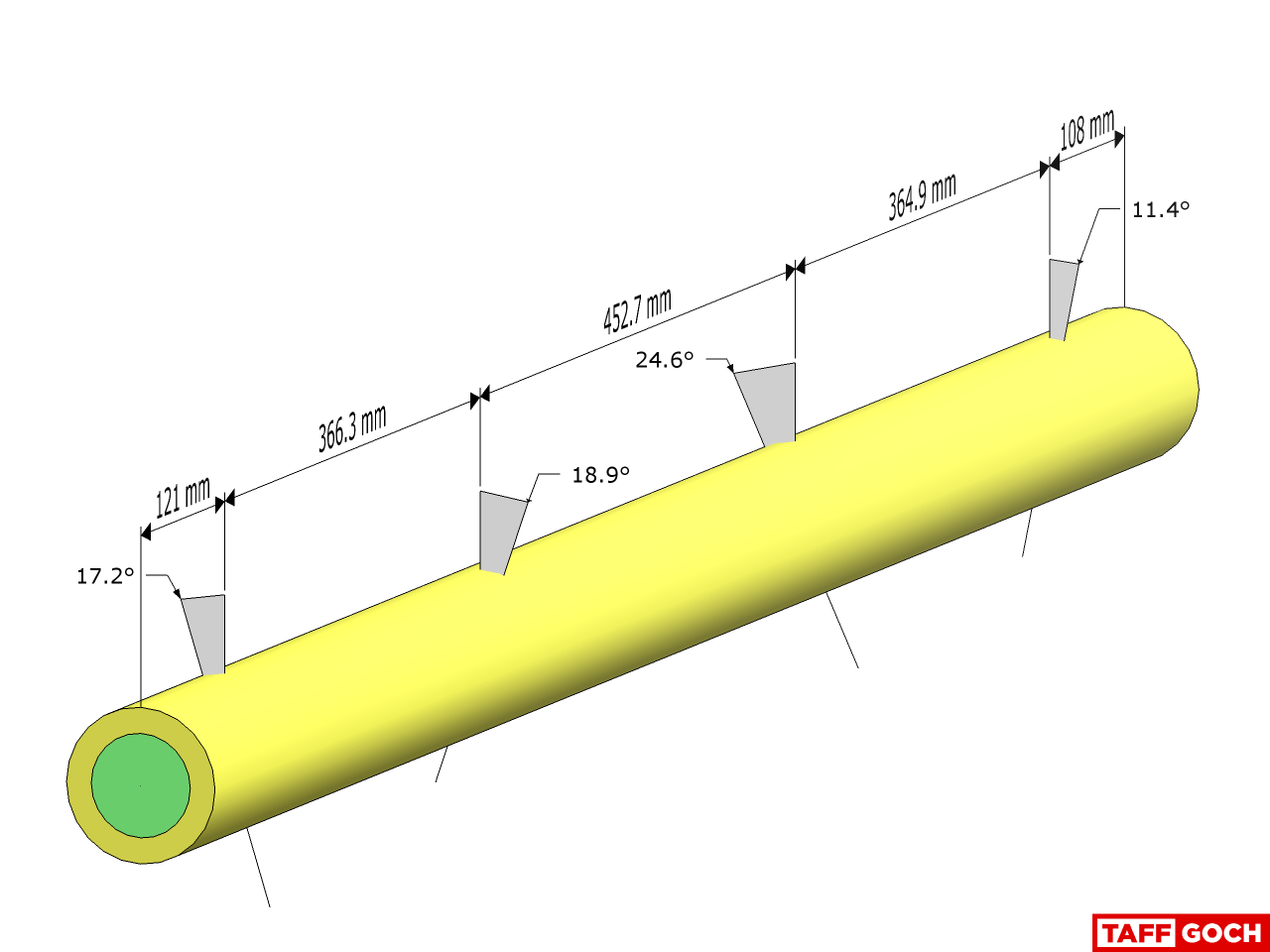
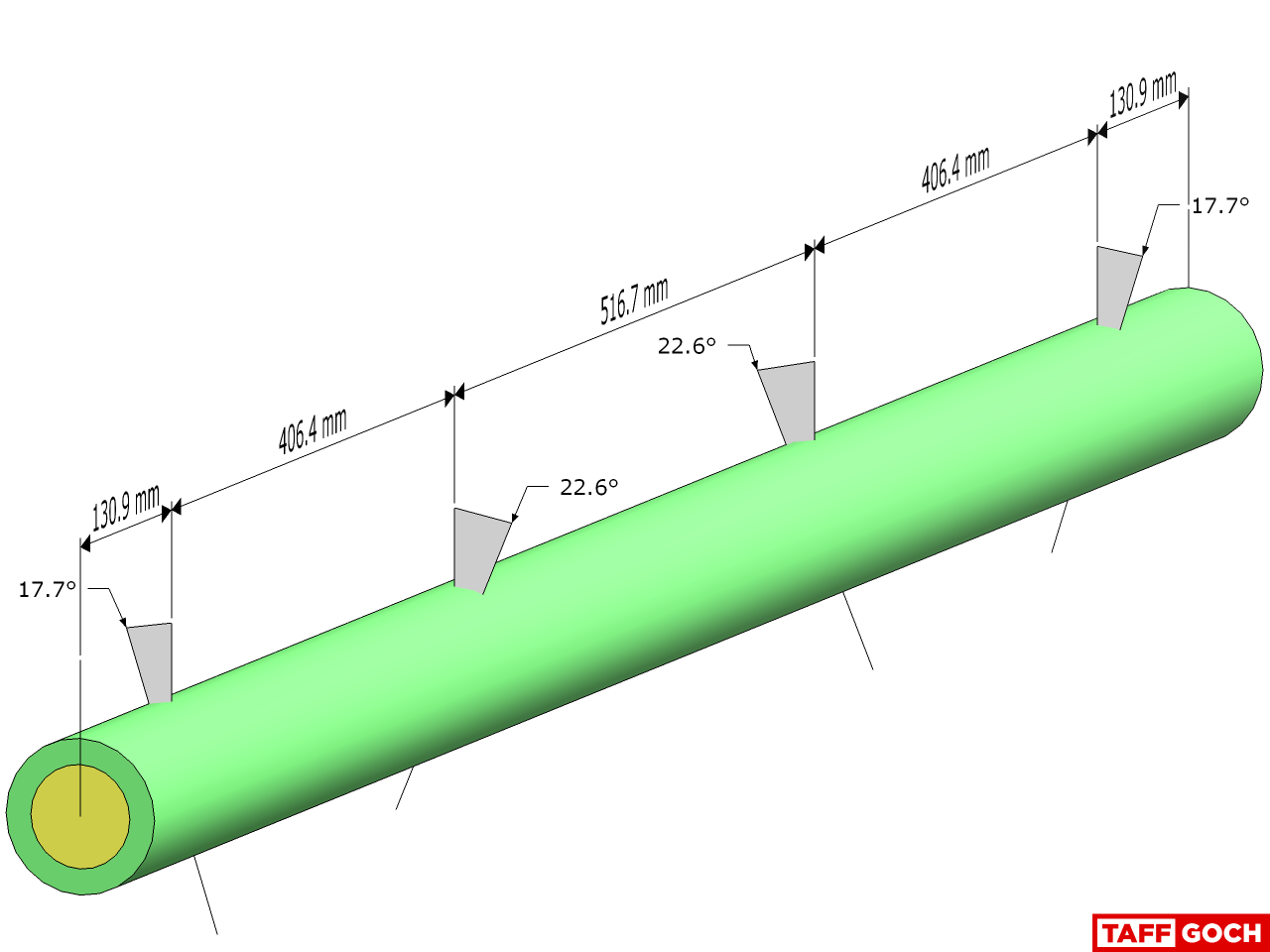
I'm thinking of building something based on this geometry. Can I ask whether the numbers in this image are chord lengths or arc lengths? That is, are they the lengths you would put between the holes before curving the rod to approximate the sphere surface, or are they the straight-line distances between the vertices of the resulting polyhedron?
(I appreciate that those two measurements will be very nearly equal, I'm just being unnecessarily obsessive about accuracy.)
On Tuesday, July 12, 2016 at 12:32:39 PM UTC+9, TaffGoch wrote:
Regarding the original nexorade post:These chord factors will produce a sphere of unit (1.000) radius. Straps are depicted, but values are valid for each of the previously-depicted nexorades. (For color-coding, refer to the "rod" or "spring" depictions.)-Taff
Patrick Doyle
Has anyone considered building a nexorade dome using the bow-roof shed construction method? Ends of the curved struts would be bolted to the other struts just as shown in TaffGoch's diagram. But, instead of being flexed and under stress, they would be rigid and more structural.
--
Bryan L
Bryan L
Dick Fischbeck
Levente Likhanecz
i succeded to repeat (build from scratch) the construct in sketchup on 100000mm radius. The 5 strut card sure listing arc lengths so my guess this 4 strut card should be same. if you wanna try it in sketchup first exchange them to chord length (fun-fact those arc lengths are equivalent to theta center angle as radians on 1.00000 radius). and use triangle built fan blade triplets. those 6 digits is not much for sharp joints. first i built the red penta fan. then between red blades the greens had minor difference to the list. then made a triangular fan of yellow-blue-purple. welded to of them along the yellow blade. that gave the most accurate 100000mm radius sphere built from top to bottom. so only the green blade was stretched on red fan all other colors used the taffgoch figures converted to cord length from arc. (sketchup measures arcs as sum of straight segments). excel attachment has some pics embedded.
Nathaniel Virgo
--
--
You received this message because you are subscribed to the "Geodesic Help" Google Group
--
To unsubscribe from this group, send email to GeodesicHelp...@googlegroups.com
--
To post to this group, send email to geodes...@googlegroups.com
--
For more options, visit http://groups.google.com/group/geodesichelp?hl=en
---
You received this message because you are subscribed to a topic in the Google Groups "Geodesic Help Group" group.
To unsubscribe from this topic, visit https://groups.google.com/d/topic/geodesichelp/RFBZ6uFmsjU/unsubscribe.
To unsubscribe from this group and all its topics, send an email to geodesichelp...@googlegroups.com.
For more options, visit https://groups.google.com/d/optout.
http://nathanielvirgo.com
Levente Likhanecz
You received this message because you are subscribed to the Google Groups "Geodesic Help Group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to geodesichelp...@googlegroups.com.