¿ Cómo funciona una ALU 74181? Explicar.
Nestor Bernardo Corpus Vergara
La unidad aritmético lógica, también conocida como ALU (siglas en inglés de arithmetic logic unit), es un circuito digital que calcula operaciones aritméticas (como suma, resta, multiplicación, etc.) y operaciones lógicas (si, y, o, no), entre dos números.
Elias Hermoza 3°B
Una ALU es un sistema que
permite realizar operaciones lógicas como OR, AND, entre otras operaciones aritméticas, por ejemplo, la suma,
resta, etc. Dentro de las ALU utilizaremos el IC 74LS181.
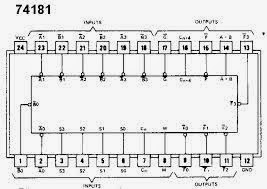
 La función de cada uno de
los pines de este IC, son:
La función de cada uno de
los pines de este IC, son:
Pines 2, 23, 21 y
19, respectivamente /A0 ... /A3, son las entradas de uno de los operandos,
activos en BAJO.
Pines 1, 22,20 18,
respectivamente / B0 ... /B3, entradas del los operandos restantes, activos en
BAJO.
Pines 9, 10, 11 y
13, respectivamente /F0 ... /F3, son las salidas de la ALU, donde se tendrán
los resultados de las entradas.
Pin 8 M , es una de
las líneas de control; por medio de esta líneas se le indica al circuito la
operación a realizar, Si M=1 realiza operaciones lógicas y realiza operaciones
aritméticas si M=0.
Pin 7 Cn, es la
entrada de acarreo esta entrada deberá ser 0 en operaciones aritméticas; en
caso de ser un 1 habrá que sumarlo a la función aritmética que se seleccione.
Pin 14 A=B, es una
salida de colector abierto e indica cuándo las cuatro salidas está a nivel
ALTO. Si se selecciona la operación aritmética de la resta es salida se
activará cuando ambos operandos sean iguales.
Pin 17 /G, salida
de generación de acarreo. En operación aritmética de la suma, esta salida
indica que la salida F es mayor o igual a 16, y en la resta F es menor que
cero.
Pin 15 /P, salida
de propagación de acarreo. En la operación aritmética de la suma, esta salida
indica que F es mayor o igual a 15 y en la resta que F es menor que cero..
Las salidas /G y /P
se utilizan par acoplar varios circuitos integrados del tipo 74181 en cascada
empleando el método de propagación en paralelo.
Pin 16 Cn+4 es la
salida de acarreo.
Pines 6, 5, 4 y 3,
respectivamente So ... S3, son las líneas de control del circuito; mediante
éstas se selecciona la función que ha de realizar el circuito.
Pin 24 = VCC
Pin 12 = GND
funcionamiento
Por medio de la
entrada M(8) ordenamos al 74181 que quieremos efectuar una función aritmética
si es nivel bajo o lógica si es nivel alto.
Luego, después de ingresar los operandos, el
circuito debe hacer en secuencia 4 operaciones, ya sean aritméticas o lógicas.
Para lograrlo debes programar las entradas
S0(6), S1(5), S2(4), S3(3) con el código de la función que quieres que realiza
el 74181.
Estos son códigos para las funciones
aritméticas que puede realizar el ALU.
Ejemplo F=9 sumamos el operando A con el
operando B y el resultado se mostrará en las salidas F.
Programar el 9 en las entradas S sería así:
S0=1
S1=0
S2=0
S3=1
Si ahora queremos realizar la función F=0 que
es restar 1 al valor de A.
Entonces tienes que programar en las S todas
en cero.
Ahora diseñaremos un
Secuenciador(Decodificador) que nos dara la secuencia de combinaciones de
números para los códigos de las funciones que quieras utilizar.
M=0 Arithmetic. (Note
**)
F=0, [A minus 1], Quiere Decir: (A-1)
F=1, [AB minus 1], Quiere Decir: (A AND B) - 1
F=2, [AnB minus 1], Quiere Decir: (A AND nB) -1
F=3, [minus 1], Quiere Decir: - 1
F=4, [A plus (A + nB)], Quiere Decir: A + (A
OR nB)
F=5, [AB plus (A + nB)], Quiere Decir: (A AND
B) + (A OR nB)
F=6, [A minus B minus 1], Quiere Decir: (A -
B) - 1
F=7, [A + nB], Quiere Decir: (A OR nB)
F=8, [A plus (A + B)], Quiere Decir: A + (A OR
B)
F=9, [A plus B], Quiere Decir: A + B
F=A, [AnB plus (A + B)], Quiere Decir: (A AND
nB) + (A OR B)
F=B, [A + B], Quiere Decir: (A OR B)
F=C, [A plus A*], Quiere Decir: A + A (Note *)
F=D, [AB plus A], Quiere Decir: (A AND B) + A
F=E, [AnB minus A], Quiere Decir: (A AND nB) -
A
F=F, [A], Quiere Decir: A
Alexander Chavez Ochoa
FUNCIONAMIENTO E IMPORTANCIA DE ALU 74181
El 74181 es una unidad aritmético lógica bit slice implementada como un circuito integrado TTL de la serie 7400 de mediana escala de integración (MSI), conteniendo el equivalente de 75 puertas lógicas y comúnmente empaquetado en un DIP de 24 pines. La ALU de 4 bits de ancho puede realizar todas las operaciones tradicionales de suma, resta, decrementar, con o sin acarreo, al igual que operaciones lógicas AND, NAND, OR, XOR y SHIFT. Están disponibles muchas variaciones de estas funciones básicas, para un total de 16 operaciones aritméticas y 16 operaciones lógicas en dos palabras de cuatro bits. Las funciones de multiplicación y división no son proporcionadas, pero pueden ser realizadas en pasos múltiples usando funciones de SHIFT y suma o resta. SHIFT no es una función explícita pero puede ser derivada de varias funciones disponibles, incluyendo (A+B) más A, A más AB.
El 74181 realiza estas operaciones en dos operandos de cuatro bits que generan un resultado de cuatro bits con un acarreo en 22 nanosegundos. El 74S181 realiza las mismas operaciones en 11 nanosegundos, mientras que el 74F181 realiza las operaciones en típicamente 7 nanosegundos.
Múltiples 'slices' pueden ser combinados para tamaños arbitrariamente grandes de palabras. Por ejemplo, seis 74S181s y cinco generadores de acarreo look ahead 74S182 pueden ser combinados para realizar las mismas operaciones en operandos 64 bits en 28 nanosegundos. Aunque fue eclipsado por el desempeño de los microprocesadores de 64 bits de multi gigahertz de hoy, esto fue absolutamente impresionante cuando comparaba a las velocidades de reloj de submegahertz de los tempranos microprocesadores de cuatro y ocho bits.
El 74181 permitió que un CPU entero y en algunos casos, un computador entero pudiera ser construido en una sola tarjeta de circuitos impresos grande. El 74181 ocupa una etapa históricamente significativa entre los CPU más viejos basados en funciones de lógica discreta extendiéndose sobre múltiples tarjetas de circuitos y los microprocesadores modernos que incorporan todas las funciones del CPU en un solo componente. El 74181 fue usado en varios minicomputadores y otros dispositivos comenzando a finales de los años sesenta, pero a medida que los microprocesadores llegaron a ser más poderosos la práctica de hacer un CPU de componentes discretos cayó en favor, y el 74181 no fue usado en ningún nuevo diseño.
jeancarlo jimenez canchan - 3 "A"
Cada bit de la ALU se procesa de manera idéntica, con la excepción del direccionamiento del bit del acarreo. El manejo de este bit es explicado más adelante.
Las entradas A y B van hacia las cuatro puertas de la izquierda, de arriba a abajo, XOR, AND, OR. Las tres primeras puertas realizan las operaciones XOR, AND, y OR sobre los datos A y B. La última puerta XOR es la puerta inicial de un sumador completo.
El paso final de las operaciones sobre cada bit es la multiplexación de los datos. La entrada OP de 3 bits, OP[0], OP[1] y OP[2] (desde la unidad de control) determina cual de las funciones se van a realizar:
- OP = 000 → XOR
- OP = 001 → AND
- OP = 010 → OR
- OP = 011 → Adición
Claramente se ve que las otras cuatro entradas del multiplexor están libres para otras operaciones (sustracción, multiplicación, división, NOT A, NOT B, etc). Aunque OP[2] actualmente no es usada en este montaje (a pesar de estar incluida y conectada), ésta sería usada en el momento de realizar otras operaciones además de las 4 operaciones listadas arriba.
Los datos de acarreo de entrada y acarreo de salida, llamados flags (banderas), son típicamente conectados a algún tipo de registro de estado.
.ENTRADAS Y SALIDAS DE LA ALU :Las entradas a la ALU son los datos en los que se harán las operaciones (llamados operandos) y un código desde launidad de control indicando qué operación realizar. Su salida es el resultado del cómputo de la operación.
En muchos diseños la ALU también toma o genera como entradas o salidas un conjunto de códigos de condición desde o hacia un registro de estado. Estos códigos son usados para indicar casos como acarreo entrante o saliente, overflow,división por cero, etc.2
En la imagen de arriba se puede apreciar una ALU TTL 74181 :Que es un circuito integrado de mediana escala de integración (MSI), conteniendo el equivalente de 75 puertas lógicas y comúnmente empaquetado en un DIP de 24 pines. La ALU de 4 bits de ancho puede realizar todas las operaciones tradicionales de suma, resta, decrementar, con o sin acarreo, al igual que operaciones lógicas AND,NAND, OR, XOR y SHIFT. Están disponibles muchas variaciones de estas funciones básicas, para un total de 16 operaciones aritméticas y 16 operaciones lógicas en dos palabras de cuatro bits. Las funciones de multiplicación y división no son proporcionadas, pero pueden ser realizadas en pasos múltiples usando funciones de SHIFT y suma o resta. SHIFT no es una función explícita pero puede ser derivada de varias funciones disponibles, incluyendo (A+B) más A, A más AB.
El 74181 realiza estas operaciones en dos operandos de cuatro bits que generan un resultado de cuatro bits con un acarreo en 22 nanosegundos. El 74S181 realiza las mismas operaciones en 11 nanosegundos, mientras que el 74F181 realiza las operaciones en típicamente 7 nanosegundos.
Múltiples 'slices' pueden ser combinados para tamaños arbitrariamente grandes de palabras. Por ejemplo, seis 74S181s y cinco generadores de acarreo look ahead 74S182 pueden ser combinados para realizar las mismas operaciones en operandos 64 bits en 28 nanosegundos. Aunque fue eclipsado por el desempeño de los microprocesadores de 64 bits de multi gigahertz de hoy, esto fue absolutamente impresionante cuando comparaba a las velocidades de reloj de submegahertz de los tempranos microprocesadores de cuatro y ocho bits.
.USO DE LA ALU EN COMPUTADORAS :
Muchos CPU y subsistemas de computadores fueron basados en el 74181, incluyendo varios modelos históricamente significativos.
- NOVA - Primer minicomputador de 16 bits ámpliamente disponible manufacturado por Data General. Éste fue el primer diseño (en 1968) en utilizar el 74181
- PDP-11 - El minicomputador más popular de todos los tiempos,4 manufacturado por Digital Equipment Corporation.
- Xerox Alto - El primer computador en usar la metáfora de escritorio y la interface gráfica de usuario (GUI).
- VAX-11/780 - El primer VAX, el más popular computador de 32 bits de los años 1980 manufacturado por Digital Equipment Corp.4 manufactured by Digital Equipment Corp.
- Three Rivers PERQ, una estación de trabajo comercial basado en el Xerox Alto y lanzado por primera vez en 1979.
- Computer Automation, un computador que encontró uso en el equipo de prueba de IC LSI y el control de proceso.
- KMC11 - Procesador periférico para el PDP-11 de Digital Equipment Corporation.
- FPP-12 - Unidad de coma flotante para el PDP12 de Digital Equipment Corp.
- CPU Wang 2200 (un 74181 por CPU) y controlador de disco (dos 74181 por controlador)
- Digital Electronics with VHDL (Quartus II Version) revisión en el Journal of Modern Engineering, Volume 7, Number 2, Spring 2007.
- A Minimal TTL Processor for Architecture Exploration un papel describiendo cómo el 74181 puede ser usado para enseñar arquitectura de CPU.
- A Hardware Lab for the Computer Organization Course at Small Colleges - Otro ejemplo como el 74181 es usado hoy en día en un ambiente de enseñanza.
- Demostración del 74181 + 74182 basada en Java
Renzo Leon Castro
Unidades de lógica y aritmética (ALU), 74181
Las ALU (Arithmetic Logic Units), o unidades de lógica y aritmética, son dispositivos muy versátiles que pueden programarse para llevar a cabo una gran variedad de operaciones aritméticas y lógicas entre dos palabras binarias. Como podremos Observar en el diagrama de pines de 74LS181, una ALU de 4 bits en tecnología TTL, consta de dos grupo líneas de entrada A3A2A1A0 y B3B2B1B0, un grupo líneas neas de salida F3F2F1F0, un grupo de líneas selectoras de función S3S2S1S0 una línea selectora de modo M, una entrada de acarreo previo Cn. una salida de acarreo resultante Cn+4, una salida de comparación A=B y dos salidas de expansión P,G.
El funcionamiento del integrado 74181 puede ejecutar 16 operaciones lógicas y 32 operaciones aritméticas diferentes con los datos de entradas A=A3A2A1A0 y B=B3B2B1B0.
Para programar el dispositivo como generador de funciones
lógicas, la entrada selectora de modo, M, debe estar a nivel alto. La operación
lógica deseada se programa mediante un código de 4 bits de la forma S3S2SISO
aplicado a las entradas selectoras de función. El estado de la entrada de
acarreo Cn es indiferente por lo cual puede fijarse en cualquier nivel.
Por ejemplo, para realizar la operación lógica A XOR B A= 1011 y B=000l, la
línea M debe estar en 1 lógico y en las líneas S3S2S1S0 debe aplicarse el
código 0110.
Cada bit de la palabra de salida F = F3F2F1F0 es el
resultado de la operación XOR de cada bit de la palabra A con el
correspondiente bit de la palabra B. Es decir, P3 =A3 XOR B3, F2 = A2 XOR B2 y
así sucesivamente. Por tanto, F = 1010.
Para programar la ALU como generadora de funciones aritméticas, la línea M debe
llevarse a nivel bajo con el fin de habilitar los acarreos internos. La suma de
A y B, por ejemplo, se realiza cuando el código de las entradas de selección es
1001. La entrada de acarreo Cn es activa en bajo.
Si la suma produce un acarreo de salida igual a 1, esté también será activo en
bajo. La ALU utiliza un sistema interno de generación de acarreos conocido como
carry look ahead (acarreo en adelanto), que no requiere que la suma sea
calculada en su totalidad antes de establecer la naturaleza del acarreo
resultante.
Daniel Layme Perez


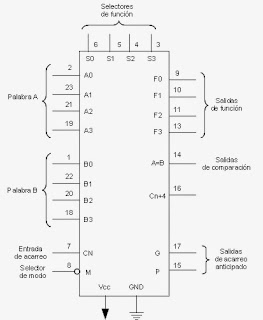
La función de cada uno de los pines es la siguiente :
Pines 2, 23, 21 y 19, respectivamente /A0 ... /A3, son las entradas de uno de los operandos, activos en BAJO.
Pines 1, 22,20 18, respectivamente / B0 ... /B3, entradas del los operandos restantes, activos en BAJO.
Pines 9, 10, 11 y 13, respectivamente /F0 ... /F3, son las salidas de la ALU, donde se tendrán los resultados de las entradas.
Pin 8 M , es una de las líneas de control; por medio de esta líneas se le indica al circuito la operación a realizar, Si M=1 realiza operaciones lógicas y realiza operaciones aritméticas si M=0.
Pin 7 Cn, es la entrada de acarreo esta entrada deberá ser 0 en operaciones aritméticas; en caso de ser un 1 habrá que sumarlo a la función aritmética que se seleccione.
Pin 14 A=B, es una salida de colector abierto e indica cuándo las cuatro salidas está a nivel ALTO. Si se selecciona la operación aritmética de la resta es salida se activará cuando ambos operandos sean iguales.
Pin 17 /G, salida de generación de acarreo. En operación aritmética de la suma, esta salida indica que la salida F es mayor o igual a 16, y en la resta F es menor que cero.
Pin 15 /P, salida de propagación de acarreo. En la operación aritmética de la suma, esta salida indica que F es mayor o igual a 15 y en la resta que F es menor que cero..
Las salidas /G y /P se utilizan par acoplar varios circuitos integrados del tipo 74181 en cascada empleando el método de propagación en paralelo.
Pin 16 Cn+4 es la salida de acarreo.
Pines 6, 5, 4 y 3, respectivamente So ... S3, son las líneas de control del circuito; mediante éstas se selecciona la función que ha de realizar el circuito.
Pin 24 = VCC
Pin 12 = GND
Luis Loreña Leon
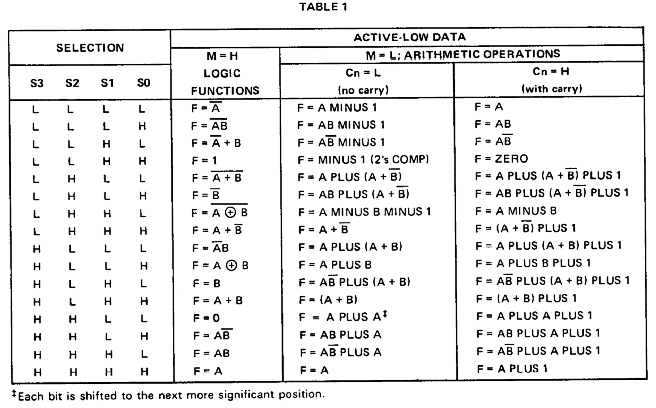
El circuito 74LS181 es una ALU que realiza 16 operaciones de aritmética binaria sobre dos operandos binarios de cuatro bits. La operación es seleccionada mediante cuatro líneas de selección de función (S0, S1, S2 y S3).Las funciones del 74LS181 se dividen en aritméticas y lógicas, usándose una entrada de “modo” (M) para escoger entre ambas funciones. Notar que las funciones aritméticas utilizan la entrada de acarreo (Cin), mientras que las funciones lógicas no.
El 74LS181 consta de:
- Cuatro entradas para el operando A.
- Cuatro entradas para el operando B.
- Cuatro entradas de selección (S0 a S3) que determina cual función lógica o aritmética debe ser calculada.
- Una entrada de modo (M) que determina si la operación a ejecutarse será lógica o aritmética.
- Una entrada de acarreo (Cin).
- Cuatro líneas de salida para el resultado (F0 a F3).
- Una salida de acarreo (Cout).
- Una salida de comparación A=B.
La ALU puede ejecutar:
- 16 operaciones lógicas.
- 5 operaciones aritméticas.
- 8 operaciones combinadas aritméticas/lógicas.
La tabla de funciones de la ALU 74LS181 es la siguiente. Tener en cuenta que el símbolo + en la tabla indica una operación OR bit a bit entre los operandos A y B, es decir que no representa una suma aritmética. La suma y resta aritmética están representadas por las palabras plus y minus.
Nota: si el valor de Cn = L (low), para activación el alto de los operandos, el resultado de la salida es el que muestra la tabla mas una unidad.
LOREÑA LEON LUIS ALBERTO 3 "A"
Jasson Rosales Astuhuaman
UNIDAD ARITMETICA LOGICA (ALU)
La ALU es un elemento polivalente que realiza operaciones lógicas y aritméticas. Antes de obtener la solución a las operaciones requeridas, es necesario comunicar a la ALU que tipo de operación se desea que realice, mediante una combinación de ENTRADAS DE SELECCIÓN. Estas entradas forman un conjunto de códigos que se denominan INSTRUCCIONES, con las que se comunica a la ALU que operación aritmética o lógica debe realizar. La ALU 74LS181 es capaz de trabajar con 2 operandos de 4 bits, que denominaremos DATOS, y las INSTRUCCIONES se componen de 5 bits.
FUNCIONAMIENTO: La función de cada uno de los pines de este C.I. se describe a continuación:
- ·
A3:A2:A1:A0 entradas del primer operando,
- ·
B3:B2:B1:B0 entradas del segundo operando,
- ·
S3:S2:S1:S0 selectores de función: mediante
éstas se selecciona la función que ha de realizar el circuito (suma, resta, multiplicación,
etc.)
- ·
F3:F2:F1:F0 salidas de la ALU, donde se tendrán
los resultados.
- ·
M: selector de Modo: sirve para determinar la
operación a realizar, Si M=1 realiza operaciones lógicas y realiza operaciones
aritméticas si M=0.
- ·
Cn: entrada de acarreo activa en nivel bajo.
- ·
A=B: es una salida de colector abierto e indica
cuándo las cuatro salidas están a nivel ALTO. Si se selecciona la operación
aritmética de la resta, esta salida se activará cuando ambos operandos son
iguales.
- ·
G: acarreo de generación. En operación
aritmética de la suma, esta salida indica que la salida F es mayor o igual a
16, y en la resta F es menor que cero.
- ·
P: acarreo de propagación. En la operación aritmética
de la suma, esta salida indica que F es mayor o igual a 15 y en la resta que F
es menor que cero.
- ·
G y P se utilizan para acoplar varios circuitos
integrados del tipo 74181 en cascada empleando el método de propagación en
paralelo.
- ·
Cn+4 es el acarreo de salida.
Programando adecuadamente las líneas de selección (S3, S2, S1, S0) y la de modo (M) junto con la de acarreo previo (Cn), la ALU puede ejecutar 16 operaciones lógicas y 32 operaciones aritméticas diferentes con selección, se relacionan en la siguiente tabla.
Rosales Astuhuaman , Jasson 3"B"
mizte...@hotmail.com
ALU son las siglas de Aritmethic Logic Unit, es decir, Unidad Lógico Aritmética.
Se trata de un circuito integrado con la capacidad de realizar diferentes operaciones aritméticas y lógicas (es decir, del álgebra de Boole), con dos palabras de n bits Se pueden encontrar como circuitos independientes, y también como bloque funcional dentro de los microprocesadores y microcontroladores.
En general, las operaciones matemáticas están codificadas en binario natural y en complemento a 2 para las restas, pero se pueden codificar en otros códigos, como por ejemplo BCD natural.
El más conocido es 74LS181, que es una ALU de 4 bits, que puede realizar hasta 32 funciones diferentes (16 lógicas y 16 aritméticas), trabaja con números binarios de 4 bits, aunque se pueden conectar en cascada para aumentar el número de bits. Este circuito integrado tiene como entradas:
- Los cuatro bits del operando A.
- Los cuatro bits del operando B.
- Entradas de selección (para seleccionar la operación a realizar, entre 16).
- Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
- Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Como salidas tiene los 4 bits del resultado, más una salida comparador (A = B) y salidas de acarreo.
Como curiosidad decir que este circuito integrado trabaja con lógica inversa en las entradas de datos y en las salidas, es decir, que para estos pines se invierte el significado de los 1 y los 0. Aunque es posible hacerlo trabajar con lógica directa.
Luis Riveros Avila
ENTRADAS:
· Los cuatro bits del operando A.
· Los cuatro bits del operando B.
· Entradas de selección (para seleccionar la operación a realizar, entre 16).
· Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
· Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Como salidas tiene los 4 bits del resultado, más una salida comparador (A = B) y salidas de acarreo.
Como curiosidad decir que este circuito integrado trabaja con lógica inversa en las entradas de datos y en las salidas.

FUNCIONAMIENTO:
Funcionalmente, una unidad del tipo 74181 acepta como datos dos palabras de cuatro bits A = A3A2A1A0 y B = B3B2B1B0, produciendo como resultado otra palabra de 4 bits F = F3F2F1F0.
Además de estas líneas posee un acarreo de entrada Cn y un acarreo de salida Cn+4, activos a nivel bajo.
La operación que se realiza sobre estos datos está determinada por las entradas de selección S = S3S2S1S0 y la entrada de modo M. Cuando M = L las operaciones son aritméticas (suma, resta, etc.), mientras que cuando M = H las operaciones son lógicas (AND, OR, etc.).
La interpretacion de la operación realizada depende del tipo de lógica que se utilice: positiva o negativa. En el caso de lógica positiva se hacen corresponder los niveles de tensión H y L con los valores lógicos H=1 y L=0.
Por ejemplo S = HLLH, M = L, A = LHHL, B = LLHH y Cn = L. La operación a realizar esta determinada por M (L: operación aritmética) Al ser Cn = L (existe acarreo de entrada) entonces la operación que se realiza es F = A plus Bplus 1. Como la lógica es positiva A = 0110 (6) y B = 0011 (3), entonces F = 1010 = HLHL (10) y no existe acarreo de salida, Cn+4 = H.
En el caso de lógica negativa se considera H=0 y L=1 y se utiliza la tabla de la derecha. Sean por ejemplo S = HLLH, M = H, A = LHLH, B = LLHL y Cn = L. La operación a realizar es lógica (M = H) y su expresión concreta es F = A ⊕ B. Al ser lógica negativa A = 1010 y B = 1101, entonces F = 0111, es decir F = HLLL.
3° "B"
Luis Salas 3 A
Las unidades aritmetico-logicas (ALU) constituyen dispositivos utiles y versatiles que implementan diferentes operaciones logicas y aritmeticas, generalmente en un solo circuito integrado. Funcionalmente, una unidad del tipo 74181 acepta como datos dos palabras de
cuatro bits A = A3A2A1A0 y B = B3B2B1B0, produciendo como resultado otra palabra de 4 bits F = F3F2F1F0 . Ademas de estas lıneas posee un acarreo de entrada Cn y un acarreo de salida Cn+4, activos a nivel bajo. La operacion que se realiza sobre estos datos esta determinada por las entradas de seleccion S = S3S2S1S0 y la entrada de modo M. Cuando M = L las operaciones son aritmeticas (suma, resta, etc.), mientras que cuando M = H las operaciones son logicas (AND, OR, etc.). Los acarreos de entrada y de salida solo tienen sentido cuando se trata de operaciones aritmeticas.
FUNCIONAMIENTO
La interpretacion de la operacion realizada depende del tipo de logica que se utilice: positiva o negativa. En el caso de logica positiva se hacen corresponder los niveles de tension H y L con los valores logicos H=1 y L=0. Sea por ejemplo S = HLLH, M = L, A = LHHL, B = LLHH y Cn = L. La operacion a realizar esta determinada por M (L: operacion aritmetica) y S (HLLH: A plus B ´o A plus B plus 1, sin acarreo y con acarreo, respectivamente). Al ser Cn = L (existe acarreo de entrada) entonces la operacion que se realiza es F = A plus Bplus 1. Como la logica es positiva A = 0110 (6) y B = 0011 (3), entonces F = 1010 = HLHL (10) y no existe acarreo de salida, Cn+4 = H. En el caso de logica negativa se considera H=0 y L=1. Sean por ejemplo S = HLLH, M = H, A = LHLH, B = LLHL y Cn = L. La operacion a realizar es logica (M = H) y su expresion concreta es F = A ⊕ B. Al ser logica negativa A = 1010 y B = 1101, entonces F = 0111, es decir F = HLLL. En esta ocasion como la operacion que se realiza es logica, los acarreos de entrada y salida son irrelevantes.
ALUMNO :SALAS CAPCHA LUIS 3 A
cro...@mepsa.com
74LS181, que es una ALU de 4 bits, que puede realizar hasta 32 funciones diferentes (16 lógicas y 16 aritméticas), trabaja con números binarios de 4 bits, aunque se pueden conectar en cascada para aumentar el número de bits. Este circuito integrado tiene como entradas:
· Los cuatro bits del operando A.
· Los cuatro bits del operando B.
· Entradas de selección (para seleccionar la operación a realizar, entre 16).
· Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
· Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Como salidas tiene los 4 bits del resultado, más una salida comparador (A = B) y salidas de acarreo.
Como curiosidad decir que este circuito integrado trabaja con lógica inversa en las entradas de datos y en las salidas, es decir, que para estos pines se invierte el significado de los 1 y los 0. Aunque es posible hacerlo trabajar con lógica directa.
Configuración de pines del CI 74LS181
Tabla con las funciones que pueden realizarse con el 74LS181
LUIS ROJAS SANCHEZ 3ro A
Grecia Almendra Uriarte Quiñones
ALU son las siglas de Aritmethic Logic Unit, es decir, Unidad Lógico Aritmética.
Se trata de un circuito integrado con la capacidad de realizar diferentes operaciones aritméticas y lógicas (es decir, del álgebra de Boole), con dos palabras de n bits Se pueden encontrar como circuitos independientes, y también como bloque funcional dentro de los microprocesadores y micro controladores.
En general, las operaciones matemáticas están codificadas en binario natural y en complemento a 2 para las restas, pero se pueden codificar en otros códigos, como por ejemplo BCD natural.
El más conocido es 74LS181, que es una ALU de 4 bits, que puede realizar hasta 32 funciones diferentes (16 lógicas y 16 aritméticas), trabaja con números binarios de 4 bits, aunque se pueden conectar en cascada para aumentar el número de bits. Este circuito integrado tiene como entradas:
- Los cuatro bits del operando A.
- Los cuatro bits del operando B.
- Entradas de selección (para seleccionar la operación a realizar, entre 16).
- Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
- Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Como salidas tiene los 4 bits del resultado, más una salida comparador (A = B) y salidas de acarreo.
Como curiosidad decir que este circuito integrado trabaja con lógica inversa en las entradas de datos y en las salidas, es decir, que para estos pines se invierte el significado de los 1 y los 0. Aunque es posible hacerlo trabajar con lógica directa.
Configuración de pines del CI 74LS181



Grecia Almendra Uriarte Quiñones 3"B"
kmj.g...@gmail.com
Cada bit de la ALU se procesa de manera idéntica, con la excepción del direccionamiento del bit delacarreo. El manejo de este bit es explicado más adelante.
Las entradas A y B van hacia las cuatro puertas de la izquierda, de arriba a abajo, XOR, AND, OR. Las tres primeras puertas realizan las operaciones XOR, AND, y OR sobre los datos A y B. La última puerta XOR es la puerta inicial de un sumador completo.
El paso final de las operaciones sobre cada bit es la multiplexación de los datos. La entrada OP de 3 bits, OP[0], OP[1] y OP[2] (desde la unidad de control) determina cual de las funciones se van a realizar:
- OP = 000 → XOR
- OP = 001 → AND
- OP = 010 → OR
- OP = 011 → Adición
Claramente se ve que las otras cuatro entradas del multiplexor están libres para otras operaciones (sustracción, multiplicación, división, NOT A, NOT B,. Aunque OP[2] actualmente no es usada en este montaje (a pesar de estar incluida y conectada), ésta sería usada en el momento de realizar otras operaciones además de las 4 operaciones listadas arriba.
Los datos de acarreo de entrada y acarreo de salida, llamados flags (banderas), son típicamente conectados a algún tipo de registro de estado.
Luis Eloy Marquez cordero 3 B
Hugo Llaja Pisco
Granados Obispo Orlando
Observen que las señales de activa en baja son negadas respecto de las de activa en alta.
Como hemos dicho anteriormente, nosotros vamos a trabajar en activa en alta tanto en los diseños
como en las simulaciones. Por tanto, para activa en alta, tanto las palabras de entrada, A3 A2 A1 A0 y
B3 B2 B1 B0, como las señales de control, S3 S2 S1 S0, M, Cn
, las interpretamos tal cual, o sea, son
directamente (sin negar) los datos que salen de los generadores de pulsos y que entran en la ALU y que
se corresponden con la cabecera de la tabla de verdad de la ALU para activa en alta. Estos serán los
valores sobre los que deberemos operar a la hora de comprobar el funcionamiento de dicha ALU.
Observen que las únicas señales que aparecen negadas son los acarreos o arrastres de entrada y salida,
Cn y Cn+4
El significado de Cn
en la tabla de verdad (de activa en alta, la del texto) es:
Cn
=H (sin Acarreo). Por tanto, su significado es Cn
= 0. O sea, Acarreo = 0
Cn
=L (con Acarreo). Por tanto, su significado es Cn
= 1. O sea, Acarreo = 1
A continuación mostramos la tabla de verdad práctica obtenida a partir del cronograma y la teórica
obtenida realizando la operación A PLUS B bits a bit (S0, S1, S2, S3) y teniendo en cuenta el acarreo
de cada bit (C1, C2, C3, C4) en la suma del bit de orden superior:
christiancco...@gmail.com
marcelo janampa "3ro "B"
Primero, sepamos qué es una proposición.
Digamos que es un enunciado, algo que digo. Este enunciado pude ser verdad o no. Pero no deja de ser un enunciado, sin importar si es o no verdadero.
Ejemplos: "Llueve", "Hace Frío", "Uso campera": son enunciados, proposiciones.
Yo sólo digo "Llueve", puede ser cierto (que este lloviendo cuando lo digo), como no. Es verdadero o falso dependiendo el momento en que se diga. Este tipo de proposiciones, que pueden ser verdaderas o falsas, y no solo verdaderas, como por ejemplo "Agua mojada" o "Sol frío", que son constantemente o verdaderas o falsas (no busquemos la vuelta acá del hielo seco, no de el sol en otro momento o en otro lugar, nada de pavadas de ese estilo: el agua es siempre mojada y el sol nunca es frío, por lo que las proposiciones estas no cambian con el tiempo, son verdadera y falsa respectivamente.
Estos enunciados, así solos, mucho no me dicen. Sin embargo, si me pongo a jugar con ellos, puedo comenzar a armar ciertas oraciones, que terminan teniendo el concepto lógico que nos va a interesar en nuestros casos.
Ya nombramos los tres enunciados que vamos a utilizar para estos juegos:
"Llueve", "Hace Frío", "Uso campera"
Ahora nombremos los conectores con los que vamos a combinarlas: los dos principales: "sí" y "entonces", y luego otros para complicar un poco la situación, que son los que van a juntar mas de una proposición: "y", "o", "no" y un cuarto que llamémoslo "xo" que es un o exclusivo, ya veremos la diferencia con el "o" normal.
Arranquemos entonces jugando a mezclar las cosas, para armar las operaciones en la forma que nos interesará analizar. Para empezar, lo más fácil: unamos dos proposiciones:
La forma de unirlas es poniendo el "sí" al principio (tener en cuenta que este es un sí no de afirmación, sino de consulta), luego ponemos "entonces", o una coma, u luego la otra proposición.
Veamos con un ejemplo, y juntemos las proposiciones que tenemos:
"Si llueve entonces uso campera".
Acá ya estoy diciendo algo, y es que "si" se da la condición de que se cumpla la primera proposición, "entonces" se tendrá que cumplir la segunda, lo que esta luego del "entonces", diciendo así que si llegase a llover, si o si tengo que usar campera, porque es mi afirmación.
Todas las proposiciones, como vimos, pueden ser "verdaderas" o "falsas".
Tenemos entonces que si la primera parte del ejemplo: "Si llueve" es una proposición verdadera, "entonces" la última parte tiene que ser verdadera, o sea, tendría que usar campera. Resumiendo, quedaría que: "Si "algo verdadero", entonces "otro algo verdadero"", es mi comparación lógica básica, juntando dos proposiciones.
Como siempre, compliquémosla un poquito, juntemos ahora las tres, con algún nexo entre las dos primeras proposiciones, para poder decir qué pasara si esta combinación de dos se cumple, con la tercera que nos queda. Y las unimos con "y", "o" o "xo".
Empecemos entonces a ver y tratar de entender qué sucede cuando ponemos el "y" en el medio, cómo influye esto en mi resultado, en lo que irá luego del "entonces".
A mezclar entonces:
"Si llueve o hace frío entonces uso campera"
Entonces, tiene que ser TODA la primera parte verdadera, para poder hacer que la tercera lo sea.
Considerando que una proposición puede ser verdadera o falsa, y en la primera parte tenemos UNIADAS dos proposiciones con un vínculo (con "o" en este caso) tenemos una combinación de cuatro posibilidades dentro de las dos proposiciones consideradas en esta primera parte (antes del "entonces"): que "llueve" sea verdad (que esté lloviendo) o que no sea verdad, que sea falso (que no esté lloviendo), y por cada una de ellas (por el caso en que sea verdadero o por el caso en que sea falso), tenemos las mismas dos alternativas para la segunda proposición, quedando así una combinación de cuatro posibilidades:
1) Que "llueve" sea verdadero "o" que "hace frío" sea verdadero
2) Que "llueve" sea verdadero "o" que "hace frío" sea falso
3) Que "llueve" sea falso "o" que "hace frío" sea verdadero
4) Que "llueve" sea falso "o" que "hace frío" sea falso
Analicemos entonces qué sucedería con cada una de las cuatro alternativas en la tercera proposición, cómo influyen en si, si la tercera se tiene que cumplir o no, considerando que el nexo de unión entre las dos, en este primer caso, es "o".
1) si está lloviendo o está haciendo frío, entonces voy a usar campera (lo voy a hacer)
2) si esta lloviendo o no está haciendo frío, entonces uso campera (lo voy a hacer)
3) si no llueve o está haciendo frío, entonces voy a usar campera (lo voy a hacer)
4) si no llueve o no esta haciendo frío, entonces no importa lo que haga con la campera.
Veamos que sucedería ahora en las mismas cuatro combinaciones, pero con un nexo "y" entre las dos primeras
1) Que "llueve" sea verdadero "y" que "hace frío" sea verdadero
2) Que "llueve" sea verdadero "y" que "hace frío" sea falso
3) Que "llueve" sea falso "y" que "hace frío" sea verdadero
4) Que "llueve" sea falso "y" que "hace frío" sea falso
Analizando…
1) si está lloviendo y está haciendo frío, entonces voy a usar campera (lo voy a hacer)
2) si esta lloviendo y no está haciendo frío, entonces no puedo afirmar nada
3) si no llueve y está haciendo frío, entonces tampoco puedo afirmar nada
4) si no llueve y no esta haciendo frío, entonces no importa lo que haga con la campera.
Veamos qué función cumple el nexo "xo", el o exclusivo. Es similar al o, pero excluye cuando las dos proposiciones primeras son verdaderas a la vez, en ese caso (que sería el primer caso en los ejemplos del "o", no puedo decir nada para mi conclusión hacia la tercera proposición, teniendo entonces:
1) Que "llueve" sea verdadero "xo" que "hace frío" sea verdadero
2) Que "llueve" sea verdadero "xo" que "hace frío" sea falso
3) Que "llueve" sea falso "xo" que "hace frío" sea verdadero
4) Que "llueve" sea falso "xo" que "hace frío" sea falso
Analizando…
1) si está lloviendo xo está haciendo frío, entonces no importa lo que haga con la campera
2) si esta lloviendo xo no está haciendo frío, entonces uso campera (lo voy a hacer)
3) si no llueve xo está haciendo frío, entonces voy a usar campera (lo voy a hacer)
4) si no llueve xo no esta haciendo frío, entonces no importa lo que haga con la campera.
Hasta ahora viene zafando el "no" que mencionamos… ya vendrá…
Pero ahora veamos qué ha ocurrido en estos tres casos.
Un detalle en particular es que en ningún momento se dijo "no voy a usar campera", sino que "no importa lo que haga con ella"…. , al estilo yanki, un "dont care"…
Por esto, más adelante veremos que lo que nos importa es cuándo las respuestas son verdaderas y no tantos las falsas (RECORDAR ESTO!!!)
NADA me dice que si no esta lloviendo ni haciendo frío no tenga que salir con campera. Si no hace frío ni está lloviendo pero tengo una gripe impresionante, o voy a un lugar donde haya que ir con campera, o sólo porque se me ocurre, y quiero usar una campera, la uso, aunque no llueva ni haga frío. A esto se lo conoce como el caso contrario a la proposición. No puedo afirmar nada en la segunda parte (luego del "entonces") si no se cumple la primera parte (antes del "entonces")
También tenemos la recíproca, que también es un "no importa". Voy de la tercera proposición a ver si puedo deducir algo de las dos primeras: si salgo con campera: implicaría esto que esté haciendo frío o que esté lloviendo? NO, PARA NADA. Como dije, yo puedo salir con campera porque se me antoja, y no por otra razón.
Ahora, la que SÍ se cumple es la contra-recíproca, que es la negación de la última parte, me implica la negación de la primera: Si NO SALGO con campera, quiere decir que ni esta lloviendo ni está haciendo frío, porque mis condiciones eran que si esto sucedía (lloviese o que hiciese frío) tengo que salir SI O SI con campera, porque es que yo afirmo. Así, la negación de la tercera, implica la negación de la parte de adelante.
Y acá metimos, medio sin querer-queriendo, el concepto de "negación", del "no"
Veamos un poco como desglosar una proposición juntada por medio de un nexo y que a la vez la estoy negando, en un par de proposiciones independientes
Para entender en base a lo que ya tenemos
1) "llueve" y "hace frío"
2) "llueve" o "hace frío"
Ahora neguemos cada una de ellas, pero al conjunto en si, a las dos de una: para este mezclemos un poco de matemáticas en nuestro lenguaje, usando unos paréntesis:
1) no ("llueve" y "hace frío")
2) no ("llueve" o "hace frío")
Veamos cómo queda esto, metiendo el "no" adentro de cada unión de proposiciones, o sea, metiéndolas adentro de los paréntesis para eliminarlos (a los paréntesis)
El primero: si mi afirmación es "llueve y hace frío", quiere decir que está lloviendo Y haciendo frío, las dos cosas a la vez (TODA una afirmación). Ahora, si quiero negar esto, podemos deducir que con que no haga sólo una de las dos cosas, mi afirmación grupal pasaría a ser falsa: si no llueve y hace frío…o… si llueve y no hace frío… o, las dos juntas… si no llueve y no hace frío…. Todas estas 3 proposiciones me niegan la primera, la grupal, que si leemos un poco detenidamente, juntando estas tres proposiciones podemos decir que niego la grupal poniendo un "o" en vez de un "y" delante de cada negación particular, quedando así: "no (llueve Y hace frío)" es lo mismo que decir "si no llueve O no hace frío" y el "o no" coloquialmente es un "ni" (OJO!!! es de un "no o" y NO de un "no y"), quedando así "si no llueve ni hace frío"
Algo similar para el segundo caso: la afirmación original a negar es: "llueve o hace frío", quiere decir que está sucediendo alguna de las dos cosas, o bien llueve o bien hace frío (o las dos cosas a la vez, ya que no es un "xo"). Bien, ahora neguemos nuestra proposición: no (llueve o hace frío) implica que no sucede todo lo que está dentro del paréntesis: razonemos un poco como meteremos el "no" adentro, como quedaría. Como dijimos recién, AL MENOS UNA de las dos cosas tiene que estar pasando para que sea verdadero, quiere decir que si meto el no adentro queda NO está… lloviendo o haciendo frío o sea que no está lloviendo y tampoco está haciendo frío. O sea queda "no llueve Y no hace frío" como verdadero para mi negación desglosada, ya que las dos negaciones a la vez tienen que darse para que sea similar a la negación grupal.
Estos dos casos son conocidos como leyes de De Morgan, y visto ya con variables:
– (A y B) = – A o –B
– (A o B) = – A y – B
Siendo A y B dos proposiciones distintas, que así las llamaremos desde ahora. Por decir (Y SOLO COMO EJEMPLO):
Si digo "A" es lo mismo que dijese "llueve", si digo "B" es lo mismo que dijese "hace frío" y si pongo un "–" es lo mismo que decir "no".
1) no ("llueve" y "hace frío") = "no llueve o no hace frío"
2) no ("llueve" o "hace frío") = "no llueve y no hace frío"
Conociendo ya las proposiciones y las variables, mencionemos entonces un caso particular de variables lógicas: las "banderas". Éste tipo de variables se usan como señalizadores de que algo sucedió o no, para poder considerar este suceso en operaciones futuras. Supongamos que hemos realizado muchas operaciones juntas, y que con una combinación en particular de estas operaciones en un momento posterior yo puedo realizar unaacción específica.
Supongamos que si llueve Y hace frío Y no hay luz O no encuentro las llaves de mi casa O tengo mucho sueño, entonces algo haré (por ejemplo, no saldré de casa). Una vez que TODAS las condiciones se dan y yo consulto si es así, yo diría: "que si llueve Y hace frío Y no hay luz O no encuentro las llaves de mi casa O tengo mucho sueño, entonces voy a poner una señalización, una variable bandera en .V.": "quedarse = .V.", voy a "activar la señal", voy a "levantar la bandera" porque esto ha sucedido. Entonces, en algún momento posterior, en los cuales, por ejemplo, puede haber dejado de hacer frío, o puedo no tener mas sueño, o cualquier otra entrada haya cambiado, pero a mí me interesa lo que había sucedido en AQUEL MOMENTO de la consulta, solamente pregunto: "es la variable quedarse = .V.?" si es así, entonces haré alguna cosa, no importando ya si en este momento no tenga más sueño.
En nuestra vida usamos para todo, en forma habitual, coloquial o la que sea, el sistema decimal. Digamos q es el más cómodo, porque contamos con los dedos, nada mas. Hay lugares donde se propone el sistema duodecimal, que es bastante mejor que el decimal, principalmente porque tiene cuatro factores propios, aparte del 1 y el 12 propio: 2, 3, 4 y 6 (digamos que el 5 no entra directamente, pero su división tiene apenas un decimal), o sea, tiene el 83% de factores propios, que lo hace un sistema bastante aplicable para "distribuir" o "repartir".
Protocolos introductorios y pensamientos propios menos, nosotros usamos el decimal y en informática se utiliza el binario (y el hexadecimal en algunos otros aspectos que no conciernen aquí) para el movimiento interno de datos.
Esto se debe a que internamente la computadora transporta electricidad, y podemos decir que en cierta fracción de tiempo (recontra infinitesimal) toma decisiones en base a dos o más estados distintos. Un estado es un estado eléctrico: hay electricidad o no la hay. Por tal motivo, pasando la parte física a la parte lógica, decimos que "tenemos" un "1" lógico (o .T.) cuando "tenemos" electricidad y que "tenemos" un "0" lógico (o .F.) cuando no la hay. O, análogamente, que "ponemos" en un "1" lógico y hacemos que haya electricidad o que "ponemos" en un "0" lógico y hacemos que no haya.
A partir de ahora y en adelante, comenzaremos a trabajar los valores lógicos con 0 y 1, y no más con .T. y .F., o "hay" y "no hay", o "verdadero" o "falso". Llamaremos con un 1 para un valor verdadero (.T.) y con un 0 para uno falso (.F.)
Tenemos así dos o tres estados distintos de entrada, que pueden poseer valores binarios equivalentes a que tengan o no una "carga lógica" en ese momento. Habitualmente esta carga lógica es el equivalente a 5 voltios físicos para un "1" o 0 voltios para un "0", pero tomar esto con pinzas, ya que no siempre es así.
Teniendo ya esas dos o tres entradas, a las que llamaremos con las variables "A", "B" o "C" (que pueden asumir nuestros valores lógicos "1" o "0")
Entonces, conozcamos este sistema. En el decimal tenemos 10 cifras, del 0 al 9. Una vez que llegamos a la última cifra, al 9, agregamos la cifra que sigue a la unidad de al lado y ponemos esa misma unidad en 0. Si a la izquierda no hay nada, obviamente pensaremos que hay un 0. Y el número que le sigue al 0 es el 1, y en la otra punta, cerrando el ciclo, luego del 9 viene el 0, comenzando nuevamente el ciclo. Entonces, arrancamos contando desde 0, seguimos con 1 y así… hasta llegar al 9. Entonces aumentamos 1 a la cifra de la izquierda y comenzamos el ciclo nuevamente en la misma columna, quedando un 1 donde había (tácitamente) un 0 y pasando el 9 a 0 para comenzar el ciclo decimal nuevamente, formando así el 10 (diez). Y volvemos a comenzar con el 1 en la segunda columna, el ciclo 0…9: 10, 11, 12… 19. Y repetimos… sumamos 1 al 1, quedando en 2 y oootra vez repetimos el ciclo en la primera columna: 20, 21… 29. Y así hasta llegar al último valor decimal en la segunda columna, el 9: 90, 91…. 99. Y acá repetimos lo anterior: sumamos un 1 al 0 tácito de la tercera columna, y ponemos a las otras 2 en 0, y comenzamos el ciclo: 100, 101…109… y sumamos 1 al 0 de la segunda, dejamos como esta la 3ra columna, y repetimos el ciclo en la primera… 110… 119… 120, 121… 129…//… 190, 191… 199 y pasamos al 200, luego al 201… y llegamos al 999, para pasar al 1000 y volver a repetir la historia.
Bueno, exactamente lo mismo sucede con el sistema binario, solo que en vez de tener 10 cifras, tenemos SOLAMENTE 2: el 0 y el 1. Así que, en este sistema, ni bien arrancamos llegamos siempre ahí nomás al final: 0… 1 y ya es el último, por lo que tenemos q sumarle un 1 al 0 tácito de la izquierda y poniendo en 0 y empezando el ciclo: 10, 11 y volvemos a sumarle un 1 al 0 tácito de la tercera columna: 100, 101, 110, 111 y arrancamos con la cuarta: 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111… y repetimos con la quinta… y así sucesivamente. Como verán en este "molesto" sistema, los límites llegan "muy rápido", por lo que siempre hay que estar actualizando las columnas, de acuerdo a la operación que vayamos a hacer.
Presentamos así los primeros 16 números binarios:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111…
Hay formas de pasar de decimal a binario y viceversa, pero no vienen al caso explicarlas, ya que no interesa el sistema decimal, sino sólo el binario, y el tema era que conozcan qué es y cómo se "cuenta", como "contamos" en el decimal.
TODO LO VISTO HASTA AHORA FUE UNA INTRODUCCIÓN PARA QUE SE CONOZCA CON QUÉ VAMOS A TRABAJAR.
En pocas palabras, tenemos proposiciones, variables y un sistema binario. Conociendo entonces todas las herramientas que vamos a necesitar para nuestro trabajo, comencemos entonces con lo que nos concierne en este ensayo: jugar con el sistema binario y aplicarle algunas de las operaciones que tienen disponibles.
Aparte de las operaciones aritméticas básicas que todos conocemos y que aplicamos en el sistema decimal, en el sistema binario comenzaremos por otras llamadas "operaciones lógicas", utilizadas en circuitos lógicos (electrónica) y en computación (programación), para luego conocer la suma y la resta (y hasta aquí llegaremos)
Operaciones lógicas, AND, OR, XOR, NOT (Y, O, O EXCLUSIVO, NO)
Aparte de nuestras tradicionales operaciones aritméticas, como la suma o la resta o la multiplicación, en informática, más específicamente en electrónica, hay otros tipos de operaciones, llamadas operaciones lógicas. Dado que en la electrónica se puede pasar todo a dos estados: "Hay corriente" o "No hay corriente", en la informática hacemos exactamente lo mismo, ya que se le mandan instrucciones a la placa madre (parte FISICA) a través de comandos binarios por medio de la programación (parte LOGICA)
Lógicamente tenemos que si le digo "0" a la computadora (programando, nivel LOGICO), le estoy diciendo "No hay corriente" a la parte FISICA (que NO EMITA corriente), y si le digo "1", le estoy diciendo "Hay corriente" (que DEBE EMITIR). De manera inversa, si la respuesta a lo que le digamos es "con corriente", a nivel programación toma el valor "1" y si me responde un "sin corriente", va a asumir un valor "0" como respuesta. Por eso la programación muy a "bajo nivel", llamándose a los lenguajes que sirven para operar muy cerca de decirle directamente las instrucciones al procesador (como el lenguaje de máquina) es básicamente combinaciones de "0"s y "1"s, por supuesto que con un paso intermedio entre el programador y el micro en donde hay un juego de instrucciones "fáciles" de entender e implementar para el programador (no sería nada cómodo programar a puro "0"s y "1"s, uno tras otro).
Como en todas operaciones, necesitamos AL MENOS dos "partes" para obtener un resultado a partir de ellas. A estas "partes" ya las llamamos "proposiciones" en nuestra introducción de lógica, las llamamos "minuendo" y "sustraendo" en la resta, "sumando" a cada uno en la suma (ya que da lo mismo poner uno delante del otro, no "vale la pena" distinguirlos como en la resta), "dividendo" y "divisor" en la división, o "factores" en la multiplicación, que al igual que en la suma, no distinguimos entre los dos porque da el mismo resultado ponerlos en el orden que sea: "el orden de los factores no altera el producto" (vox populi, según Manolito). Y, de cada una, tenemos un resultado principal y a veces alguno extra. Más adelante hablaremos de estos extras, como por ejemplo el resto de una división (no es taaaan así tampoco el extra, pero es para que vean que puede haber algo mas aparte de los resultados…)
Pues bueno, acá, con la lógica, también tenemos 2 elementos de entrada y uno (o dos) elementos de salida. A estos "elementos" los llamaremos "variables", dado que cambian con el correr del tiempo. Y, habitualmente, las llamaremos variables "A" y variable "B" (sin las comillas) y "R" a la respuesta (y "C" al extra)
En las operaciones lógicas, la variable "C" no juega. Así que tenemos solamente dos variables de entrada (A y B) y una de salida (R).
Pongámonos de acuerdo y aceptemos que tanto A como B como C o como R pueden valer solamente 0 o 1 y ningún otro valor, solo valores binarios.
Antes de arrancar, y para marearlos un poquito, vamos a decir que también podemos operar con sólo una variable (A o B) y, en base a una de las operaciones del título, tener una respuesta R. Esta operación es la negación, el complemento, el inverso, el NOT, el NO, el "–" , como quieran llamarlo. Así:
– A = NOT(A) = NO (A)
En donde, si A es 1, el negativo de A es 0, y si A valiese 0, su inverso es 1.
O sea, si yo le aplico la función NOT(A), y si A valiese 1, la respuesta (R) tomaría el valor 0
Si A = 1, entonces:
NOT(A) = 0
Y si A = 0
NOT(A) = 1
Entremos ahora a las otras tres operaciones lógicas: AND (Y), OR (O) y XOR (O exclusivo)
Si nos acordamos algo de lo que vimos atrás en la introducción de lógica proposicional, el resultado a la operación de las dos primeras proposiciones, depende pura y exclusivamente de ellas (de las proposiciones) y de la operación lógica que las vincule.
La primera: AND (Y), conocida como "multiplicación".
Aquí, LA UNICA respuesta R es Verdadera (valor 1, hay corriente) es cuando las dos proposiciones (las dos variables de entrada: A y B) son verdaderas (LAS DOS son 1, en las dos hay corriente). De cualquier otra forma, la respuesta R es falsa (valor 0, no hay corriente). Su "tabla lógica" es:
A B R
0 0 0
0 1 0
1 0 0
1 1 1
Con este tipo de "tablas" de doble entrada trabajaremos para mostrar los valores de las respuestas R en base a las proposiciones anteriores A y B (y C)
Se le dice multiplicación, porque si en vez de "Y" pongo un "por", el resultado es el mismo: 0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0 y 1 x 1 = 1
La segunda: OR (O), conocida como "suma"
Aquí, las respuestas R son Verdaderas siempre y cuando CUALQUIERA de las dos proposiciones A o B valgan 1. CUALQUIERA DE LAS DOS O LAS DOS A LA VEZ.
Su tabla lógica es:
A B R
0 0 0
0 1 1
1 0 1
1 1 1
Se le dice suma, porque si ponemos el "mas" en lugar del "O", el resultado es el mismo:
0 + 0 = 0, 0 + 1 = 0, 1 + 0 = 0 y 1 + 1 = 1 (es 2, pero en realidad es un "hay", así que el valor es 1). En el caso de la suma en sí, veremos que 1 + 1 no va a ser ni 2 ni 1, sino 10 (valor binario de 2), o sea que R valdrá 0 y comenzarán los problemas con los terceros en discordia (las variables C que ya nombre antes, que es a donde irá a parar ese 1). Pero no nos adelantemos, asumamos esto así y listo: 1 + 1 = 1 cuando es un "O" y listo.
La tercera: XOR (o exclusivo)
Es muy parecida a la O, solamente que si A y B valen 1, R vale 0. Como bien dice, es un O exclusivo, R es 1, solamente si O BIEN A vale 1 O BIEN B vale 1, PERO NO LOS DOS.
Su tabla de verdad:
A B R
0 0 0
0 1 1
1 0 1
1 1 0
Extendamos un poco más el tema, pensemos qué pasaría si hubiesen más de 2 variables de entrada. U obtenemos esta respuesta pensando y deduciendo, o lo hacemos co un alguna regla matemática. Para las dos primeras, podemos pensar primero, y después aplicamos algunas vueltas matemáticas para ver y comparar resultados.
Para el "Y" es de entender que la única forma de que haya una respuesta Verdadera, es que ABSOLUTAMENTE TODAS las variables de entrada (sean cuantas sean) sean verdaderas.
De igual forma, pensando un poco, para la variable "O", tenemos que POR LO MENOS UNA de las variables de entrada sea verdadera, para que la respuesta sea verdadera. Pude ser una sola verdadera y las otras diez (por decir un número) sea falsa, la respuesta entonces es verdadera.
La o exclusiva, como no es de uso coloquial, sino mas de informática o de electrónica, no podemos "deducir" su comportamiento razonando. Así que abusemos un poquito de las matemáticas.
Pensemos que si tenemos 3 entradas (serían las variables A, B y C) con un MISMO nexo de unión entre ellas (un "OR", un "AND" o un "XOR"), podemos hacer la operación con las dos primeras variables (por dar un orden, nada mas, podrían hacerlo con dos que quieran primero y después usarían la que queda), obtener una variable R de salida, y a esta variable de salida le aplicamos esa misma operación con la variable que sobra, obteniendo el resultado que queremos. Veamos los resultados con algunas tablas lógicas:
AND
A B R(parcial) C R(final)
0 0 0 0 0
0 1 0 0 0
1 0 0 0 0
1 1 1 0 0
0 0 0 1 0
0 1 0 1 0
1 0 0 1 0
1 1 1 1 1
OR
A B R(parcial) C R(final)
0 0 0 0 0
0 1 1 0 1
1 0 1 0 1
1 1 1 0 1
0 0 0 1 1
0 1 1 1 1
1 0 1 1 1
1 1 1 1 1
Con el que queda, con el X-OR, vamos a dar el ejemplo con 3, pero para ver un poco como seguiría el tema, tendrían que hacerlo con cuatro y, eventualmente, con 5 y 6. Pero vamos a ver sólo con 3 y tratar de deducir, en base a ver el resultado en la tabla, que sucedería si avanzásemos con más variables
X- OR
A B R(parcial) C R(final)
0 0 0 0 0
0 1 1 0 1
1 0 1 0 1
1 1 0 0 0
0 0 0 1 1
0 1 1 1 0
1 0 1 1 0
1 1 0 1 1
Como vemos (yo lo veo, espero ustedes también) cuando con las dos primeras hay SOLO UNA verdadera, la respuesta sale verdadera, y después, si la tercera es verdadera, al ser la respuesta anterior verdadera, dos verdaderos dan falso de resultado (dado que es exclusivo). Pero si la tercera es falsa, siendo la primera (la respuesta en este caso) verdadera, la salida es verdadera. Ahora, si la salida es falsa (o las dos primeras variables son verdaderas, o las dos primeras variables son falsas), y la tercera variable es verdadera, entonces tenemos una R final verdadera, pero si la tercera variable es falsa, obtendremos, como es de esperar, una salida falsa.
Si ven un poco, verán que tenemos una salida general positiva SIEMPRE Y CUANDO SOLO una de las 3 variables es verdadera, PERO TAMBIEN es verdadera cuando LAS TRES lo son a la vez. Y la salida sería falsa, cuando son TODAS las entradas lo son o cuando DOS de las variables son verdaderas y la que sobra es falsa. Si seguimos agregando otra cuarta variable (una tal D), veremos que sigue comportándose de la misma manera (la salida temporal junto al valor de la nueva variable). Y así… Conclusión: la salida es verdadera SIEMPRE Y CUANDO UN NÚMERO IMPAR DE ENTRADAS SEAN VERDADERAS Y ES FALSA SIEMPRE Y CUANDO UN NUMERO PAR DE ENTRADAS LO SEAN (considerando al 0 como número par, ya que el resto de 0 dividido 2 es 0, por lo tanto es par). Por tal motivo se lo conoce como "detector de imparidad".
Suma
Veamos cómo sumamos en nuestro sistema, el decimal:
123 (sumando 1)
+
275 (sumando2)
----
398 (resultado, suma)
Comenzamos desde la derecha hacia la izquierda, y vamos sumando uno a uno cada par de dígitos de los distintos sumandos, y vamos formando el resultado de la suma: 3 + 5 es 8, y lo ponemos abajo, 2 + 7 es 9, y lo ponemos abajo, 1 + 2 es 3, y lo ponemos abajo, y tenemos así el resultado total de nuestra suma, leído de izquierda a derecha: 398.
Ahora, por que lo hacemos de izquierda a derecha, y no al revés? Supongo que ya conocerán la respuesta: por si aparece algún "me llevo uno" en el medio, que es lo que vamos a ver en el siguiente caso (por supuesto que para empezar, empezamos fácil y la vamos complicando de a poco). Veamos entonces como era esto del "me llevo uno":
258
+
125
----
383
Cómo hicimos? Otra vez, de izquierda a derecha: 8 + 5 = 13, pongo el 3 y "me llevo uno" a la columna anterior (o siguiente, depende del punto de vista: es anterior en el papel, y es la siguiente en que es la próxima a sumar): 1 (que traje de la suma de la columna anterior) + 5 + 2 = 8, y no me llevo nada, así que 2 + 1 es 3 y listo
215 8
+
1 2 5
-------
3 8 3
Y así podemos llevarnos unos cuanto "me llevo uno" seguido o salteados:
478659
+
289172
----------
767831
Con los "me llevo uno" metidos, quedaría:
417 81615 9
+
2 8 9 1 7 2
-------------
7 6 7 8 3 1
Entonces así, cuando aparece un "me llevo uno" de la columna, anterior, que correctamente tendríamos que decir "me llevo 10" y no 1, sumamos los valores de las cifras de las dos columnas y le sumamos 1, y si no aparecen, sólo sumamos los dos valores y nada más. Después, con el resultado obtenido de sumar estas dos o tres cifras, veremos mi "me llevo una" a la columna que sigue…
Entendamos entonces que, aparte de las dos variables comunes (los dos sumandos), acá ya empiezan a aparecer complicaciones, y sepamos diferenciar bien las dos complicaciones: el "me llevo uno" y el "más uno que me llevaba". Uno manda a la próxima, y el otro lo traigo de la anterior. Uno usamos en la suma esta y viene de la anterior, y al otro lo mandamos a la que sigue, y en actual NO SE USA.
Espero esto se haya entendido bien, ya que es elemental para lo que sigue: la suma binaria
La suma entonces…
1001011000
+
0010100010
---------------
1011111010
Por supuesto que para empezar, no nos llevamos nunca un regalito a la siguiente columna, y todo es fantástico así, pero saben perfectamente que a la situación hay que complicarla, y tenemos que ver los casos donde debemos "llevarnos uno". Hagámoslo entonces:
1001110010
+
0011101011
---------------
1101011101
Uno por uno: 0 + 1 = 1 y no llevo uno; 1 + 1 es 10 (2 binario) así que acá comenzamos: pongo el 0 y "me llevo" uno (o sea 10, correctamente) a la columna que sigue, en donde ya tengo 0 + 0 y a estos le sumo el 1 del "me llevo", así que me queda: 1 + 0 + 0 = 1 y no me llevo nada (está mal dicho "no me llevo nada" , ya que doble negación sería afirmación, pero así hablamos, que le vamos a hacer, lo correcto sería "no me llevo algo", pero dejémoslo así…). Sigamos entonces: 0 + 1 sin nada traído, es 1 y nada lleva; 1 + 0 + nada = 1 y nada llevo; 0 (no traigo nada) + 1 + 1 es 10 otra vez, pongo el 0 y me llevo 1; tenemos en este que viene el otro caso: 1 "que me llevaba" + 1 + 1 = 11 (3 decimal), pongo entonces el 1 (el de la derecha) y "me llevo uno" (otra vez, 10 en realidad); 1 (que me llevaba) + 0 + 1 = 10, pongo el 0 y me llevo 1; 1 (que traigo) + 0 + 0 = 1 y no llevo nada; 0 + 1 + 0 = 1. y listo!
1101011 1 1 010 1 0
+
0 0 1 1 1 0 1 0 1 1
-----------------------
1 1 0 1 0 1 1 1 0 1
Veamos cada caso en particular:
Primero, sin los "y uno que me llevaba"
A es 0 y B es 0, el resultado es 0 y nada me llevo (0 entonces)
A es 0 y B es 1, el resultado es 1 y nada me llevo (0 entonces)
A es 1 y B es 0, el resultado es 1 y nada me llevo (0 entonces)
Ahora empezamos con los problemas:
A es 1 y B es 1, el resultado es 10, así que es 0 y me llevo 1
Ahora cunado tengo un "y uno que me llevaba"
1 + A es 0 y B es 0, el resultado es 1 y nada me llevo (0 entonces)
1 + A es 0 y B es 1, el resultado es 0 y me llevo 1
1 + A es 1 y B es 0, el resultado es 0 y me llevo 1
Y acá el caso "más complicado"
1 + A es 1 y B es 1, el resultado es 11, así que es 1 y me llevo 1
De esto, acá tenemos la tabla lógica de la suma
|
C |
A |
B |
R |
V |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
Un poco de la nomenclatura usada:
Variables A, B y R ya las conocen (A, B y Respuesta). Y aparecen otras dos, una es de entrada: la C, el "más uno que me llevaba" (que está en 1 si efectivamente me traje uno de la suma anterior, o está en 0 si nada me he traído), y la otra es de salida, la V, que viene a ser el "me llevo uno" para la próxima. O SEA: Si V es 0, C en la próxima operación es 0, y si V es 1, C en la próxima operación es 1.
Y con todas estas variables, hacemos la suma binaria.
El párrafo que sigue es para marearlos un poquito. Es la verdad del tema, que desvirtúa un poco lo visto con estas dos variables nuevas que aparecieron. Pueden seguir creyendo las cosas así como están, o entender la verdadera forma:
La variable V es una bandera para activar y poner a C en el estado acorde en la siguiente operación. Si esta bandera está en 0 (Falso), significa que todo está bien, que nada pasó. Pero si esta bandera V está en 1, significa que "algo pasó". Entonces lo que verdaderamente hace la computadora es "levantar" la bandera (la pone en 1) avisando que "me llevo uno" a la próxima suma, o "la baja" (la pone en 0) si no se lleva nada. La operación posterior "mira" como está esa bandera, y si está "levantada", se pone alerta porque sabe que algo distinto tiene que hacer, y, en este caso, sería poner a la variable C (Acarreo o Carry) en 1; y si estuviese abajo (o apagada), significa que todo está bien, y C vale entonces 0 (o no considero nada más para la suma, y sumo sólo A y B, solamente las dos variables de entrada). En el caso de la suma, a esta bandera de salida la llamaremos OVERFLOW (desbordamiento, la suma se pasó a un valor más alto de lo que puede valer) y la llamamos con la letra V.
Resta
Para empezar con esto, vamos a recordar los métodos de resta que ya conocemos, en sistema decimal.
Vamos al más simple:
456 (Minuendo, sólo para recordar, y así lo llamaremos)
-
142 (Sustraendo)
-----
314 (Resto y diferencia)
Avancemos un poco:
452
-
126
-----
326
Acá expliquemos qué hicimos en el sistema decimal: como 2 es menor q 6 y no le puedo sacar 6 a dos, entonces le pido 10 unidades al número precedente (al 5) quedando este (el 5) en 4 y el 2 en 12. Ahora si, a 12 le puedo restar 6, quedándome 6 en la diferencia. Después hago 4 (así había quedado el 5) menos 2, queda 2, y 4 – 1, queda 3.
4412
-
12 6
-----
326
Compliquémosla un poco más:
703
-
467
-----
236
Expliquemos esto ahora: 7 no entra en 3, así que tiene que pedirle 10 al número anterior. Pero resulta que este numero es un 0, y no le puede dar nada, así que tiene que pedirle a su anterior para poder restar, al 7, quedando así, en hilera, el 7 en 6, el 0 en 9 y el 3 en 13
6913
-
46 7
-----
236
Y, sobre este mismo caso, supongamos q tenemos:
70002
-
31234
--------
38768
Aplicando lo mismo de antes, el primer 0 le pide al anterior, que también es 0, así q le tiene que pedir nuevamente al anterior, que vuelve a ser 0, así que le pide a su anterior también, al 7 (al fin!), quedando:
699912
-
3123 4
--------
38768
Por qué tanto hincapié en el pedido cuando hay 0? Fácil: en binarios hay sólo 0 y 1, y la posibilidad de que aparezcan es de un 50% contra un 10% en el decimal, por lo que nunca le dimos tanta importancia al tema.
Veamos ahora otra forma de restar, a través del complemento de un número: viene a ser la diferencia que hay entre este número y su número natural potencia de diez más cercano hacia arriba. Para hacerla mucho más fácil, le restamos 1 y luego se lo sumamos.
Así, el complemento de 467 es 1000 (número potencia de 10 más cercano hacia arriba, más fácil, un 1 y la misma cantidad de dígitos que el número dado en 0s) -1, o sea, 999, mas fácil todavía, pongo la misma cantidad de 9s (que viene a ser el número más grande del sistema decimal, recordar esto !!!) + 1 nuevamente.
Así, el complemento de 467 es: 999 (1000-1) – 467 + 1 = 533
Entonces ahora en la resta que teníamos: 703 – 467, le sumamos a minuendo (el 703) el complemento del sustraendo (de 467) que ya averiguamos antes, que era 533, y descartamos el 1 final que sobra:
703
+
533
-----
1236
Sacamos el 1 del principio (digamos q le sacamos los 1000), y voila!, nos queda 236, que es lo mismo que 703-467 !!!
Con todo esto, deducimos que tenemos 4 componentes principales en la resta: Minuendo, Sustraendo, Resto y un tal "le pido"
Ya hemos tenido una breve introducción, un breve recordatorio, a la resta en el sistema "humano", el decimal, con algunas explicaciones extras a lo que nos enseñaron en la escuela.
Bueno, ahora pasemos a la resta pero en el sistema de la computadora, o sea, el decimal
Primero veamos en decimal "humanizado", sin pensar en cómo lo hace la computadora, y luego veremos una diferencia con el sistema empleado por la computadora.
A partir de ahora, llamaremos al minuendo: "A", al sustraendo: "B", al resultado: "R" y al "le pido": "C"
Igual que antes, empecemos fácilmente:
0 - 0 = 0
1 – 0 = 1
1 – 1 = 0
Y se acabó lo fácil. Ahora empecemos a complicarla, de a poco…
0 – 1 = ….
Le tengo que pedir al anterior, y tenemos:
110
-
001
----
101
El 0 le pide al 1, que le puede dar, así que el 1 queda en 0, y el 0 queda en 10, asi 10-1 = 1 (pensar en binario!!!, sino pensar que 102 es 210 y 2-1 es 1 y listo!):
1010
-
00 1
-----
10 1
Digamos que está fácil, todavía, entonces hagámosla más difícil:
111000010110
-
001010101100
------------------
…………………
Acá: 0-0=0, 1-0=1, 1-1=0, y arrancamos: 0-1 = 10 (pedido 1) – 1 = 1. El 1 anterior le puede dar, así que no hay problema. Luego 0 (1 convertido) – 0 = 0. En el próximo, el 0-1 vuelve a pedir, pero como el anterior es un 0, le pide al anterior, que es otro 0, asi que le pide a su anterior y así hasta llegar al primer 1 bondadoso que aparezca. Recordando que en el sistema decimal todos los 0 que quedan "en el medio" quedan en "9" (el decimal mas grande), aquí pasa lo mismo: todos "los del medio" quedan en 1. Ahora los extremos: el bondadoso donante queda en 0 (1-1) y el primero que pidió, al igual que antes, queda en 10, asi: 10-1 = 1 y todos los 1 "del medio" (les dije que se acuerden de este tema con los 9…) pueden operar fácilmente (como lo harían los "9") ya que su sustraendo nunca puede ser mayor que el, entonces sigue el tema digamos que fácilmente:
1101111010110
-
001010 101100
-------------------
101101 101010
Al 0 convertido no le alcanza, por lo que le pide al anterior, quedando en 0 y 10 (igual que lo ya visto…)
Complemento en binario.
Es el mismo caso que en el decimal: busco el número q complementa a su número potencia 2 de misma cantidad de dígitos que el mismo, y luego le resto 1. En binario, tenemos que ese numero, así como en decimal era 99999…, es 1111111, y, de la misma forma, si yo resto cualquier número a 9999…. No le tengo q pedir nunca nada a nadie, y luego sólo sumo, acá pasa lo mismo:
111000010110 (12 dígitos)
-
001010101100 (12 dígitos)
------------------
El complemento de 001010101100 es restarle a 1000000000000 (un 1 y 12 0s, la misma cantidad de dígitos que 001010101100), que vendría a ser lo mismo que restarle 1 al 1000000000000, quedándome: 111111111111 y luego de la resta, se lo vuelvo a sumar. Así, el complemento de 001010101100 sería:
11111111111
-
001010101100
------------------
110101010011
Que, si bien lógicamente es la diferencia entre un número y otro, visto con ojo humano, donde hay un 1 pongo un 0 y donde hay un 0 pongo un 1
Ahora le sumo 1: 110101010011 + 1 = 110101010100 (ver suma de binarios si no se entiende esta suma)
Ahora entonces sumo a A el complemento de B más el 1 ese:
111000010110
+
110101010100
------------------
101101101010
Con un 1 adelante, que, al igual que en el sistema decimal, lo elimino…
Bueno, todo esto es a nivel binario humano, tanto el pedir prestado de a más de uno hacia la izquierda, como la diferencia por número complementario. Esto se hace para facilitarnos a nosotros, las personas, el tema. Ahora, en informática, como sabemos, la computadora no piensa, no razona, no le puedo decir que haga un complemento, para que después reste de este (haría dos operaciones en vez de una), como tampoco podemos decirle que empiece a pedirle al otro y al otro y así, si no le alcanza. No puede ir "tan" allá a pedir. Sólo podemos pedirle al anterior y nada más. Bueno, en esto se basa en cómo trabaja la computadora. Como dijimos, no razona, por lo que se analizaron todas las situaciones de juego, se vieron los resultados, se analizaron, y se le dijo a la computadora: "dada las siguientes situaciones, vos tenés que hacer esto…", que es lo que veremos ahora.
Por lo visto, vamos a tener nuevamente al minuendo en A, al sustraendo en B, al resultado en R, y al "le pido", que llamaremos acarreo, en C. El acarreo va a cumplir un papel importante en la resta binaria informática, al igual que lo cumple el acarreo en la suma: el overflow, el "me pase, así que llevo 1 al de la izquierda" (o 10, que por pasar a la columna anterior, pasa 1), sólo que en el caso de la suma hace exactamente lo mismo que en la suma humana, por eso es mas fácil. Acá, en la resta, vamos a hacer un combinado de cosas que terminan mareando un poco. Para empezar, nuestro acarreo es una bandera, un avisador de que en el cálculo anterior (en forma humana, el cálculo de la columna anterior) no le alcanzó con lo que tenia, así que su diferencia le habría dado negativa, por lo que le ha tenido que pedir uno al cálculo que sigue.
Entendamos que la computadora hace también de derecha a izquierda, desde el bit menos significativo al bit más significativo, pero hace los cálculos de a uno, sin siquiera saber nada de lo que hay después, qué viene después. Si llega a pedir, no sabe si el que sigue le va a poder dar o no, sólo pide, y lo hace activando el acarreo, prendiendo una bandera, poniendo a C en "1".
Con esto tenemos que en las operaciones de resta, al igual que en las sumas, trabajamos con 3 datos de ingreso, y tenemos dos salidas: "A", "B" (minuendo y sustraendo) y "C", el acarreo del cálculo anterior para las entradas, y "R" (resultado, resto, diferencia) y "N" como acarreo para el próximo cálculo, que estaría en "0" si no hubiese pasado nada o en "1" si hubiese tenido que pedir prestado. Todos estos valores, como bien sabemos, pueden valer solamente "0" o "1". Llamamos al último "N" para no confundirlo con "C", por más que ya se estén dando cuenta que el "N" de un cálculo pasa a ser el "C" del cálculo inmediato posterior, y porque es la bandera "Negativo" en el registro de estado.
Mucho bla bla, mucha teoría introductoria, pero es necesaria para entender lo que viene, que es ver ya como hace la ALU de la computadora una resta.
Empecemos sabiendo que todas las banderas del registro de estado están apagadas (están todas en "0", así que nuestro primer "C" es 0, nadie le pide nada al primer cálculo que vayamos a hacer.
Los valores de "A" o "B" son los que se den para el cálculo.
Tenemos entonces para ver, al igual que en la suma, 23 = 8 combinaciones entre "A", "B" y "C" para la resta
Así tenemos para empezar:
C en 0:
A en 0 y B en 0: 0-0 sin acarreo, es 0 (R) y no pide nada (N=0)
A en 1 y B en 0: 1-0 sin acarreo es 1 (R) y no pide nada (N=0)
A en 1 y B en 1: 1-1 sin acarreo es 0 (R) y no pide nada (N=0)
Como antes, hasta acá lo fácil:
Con entrada C en 0, A en 0 y B en 0, tenemos R en 0 y N en 0
Con entrada C en 0, A en 1 y B en 0, tenemos R en 1 y N en 0
Con entrada C en 0, A en 1 y B en 1, tenemos R en 0 y N en 0
Las tres primera combinaciones de 8, las más fáciles.
Como antes, con la siguiente, comienzan los problemas:
A en 0 y B en 1: 0-1 (sin acarreo, C es 0) es 1 (R) y ahora ya pide (N=1)
Por qué es 1 esta diferencia? Porque pidió, como ya dijimos, no importa a quien, sólo pidió 1. Él pidió al anterior, no importa si puede darle o no, sólo le pidió. Y asumimos que alguien, en algún momento, le podrá dar, así que pasa a valer, como en el caso visto antes, 10 (2 decimal), un 1 a la izq de él (0).
Así, 10 – 1, como antes, es 1. O sea, R vale 1 y N vale 1, porque pide.
Tenemos acá el cuarto caso de los 8, el más fácil de los difíciles:
Con entrada C en 0, A en 0 y B en 1, tenemos R en 1 y N en 1
Con este cuarto caso se acabaron las combinaciones con el acarreo (C) en 0. A partir de ahora, veremos las 4 restantes, que serían las 4 combinaciones posibles entre A y B, pero con C en 1, o sea, asumiendo que le está prestando a alguien que le pidió antes. Igual que antes, arranquemos con el más fácil de los 4: que A valga 1 y que B valga 0:
A en 1 y B en 0: 1-0 (con acarreo, C es 1) es 0 (R) y ahora no pide nada (N=0)
Fácil de entender que si A era 1 y le podía dar al anterior, se lo da y pasa a valer 0, quedando así que 0-0 es 0. PERO, esto es visto a ojo humano!!. Si bien esto es lo correcto, asumamos ahora que el acarreo trabaja con los demás, con A y B, así, 1 (C) – 1 (A) – 0 (B) es 0. Digamos que es la forma en que tenemos que empezar a verlo, metiendo al acarreo en la resta misma, de 3 números.
Con entrada C en 1, A en 1 y B en 0, tenemos R en 0 y N en 0
Con esta van 5, quedan 3 todavía…
Veamos la que le sigue en dificultad:
A en 1 y B en 1: 1-1 (con acarreo, C es 1) es 1 (R) y pide 1: N = 1
Veamos qué pasó: como C es 1, A pasaría a valer 0 (por prestarle al que le pidió), y como no puedo restar 0 (el nuevo valor de A por haber prestado) – 1 (valor de B), así que quedaría pidiendo al próximo (N=1). Ahora, igual que antes, pensémoslo combinando el acarreo con los valores reales de A y B (todos en 1, como vinieron originalmente): 1 (C) – 1 (A) – 1(B) = 0 (C – A) – 1 (B) = 10 (y vuelve a pedir) – 1 (B) = 1 pidiendo 1, o sea:
Con entrada C en 1, A en 1 y B en 1, tenemos R en 1 y N en 1
Y así la sexta combinación… quedan 2, las más complicadas, con acarreo (C en 1) y A en 0, el postre del tema…
Empecemos por la más fácil de las dos, cuando B vale 0, tenemos entonces:
A en 0 y B en 0: 0-0 (con acarreo, C es 1) es 1 (R) y pide 1: N = 1
Veamos en detalle qué pasó acá: en forma humana estamos en la situación de que se le está pidiendo un valor al minuendo desde número anterior, pero A está en 0, por lo que no le puede dar el pedido, así que directamente pasaría a pedirle al anterior. De esta forma, de una nomás, N pasa directamente a valer 1, al igual que ocurrirá en el caso siguiente (así, siempre que le estén pidiendo a A, con C en 1, y A esté en 0, sí o sí va a tener que pedir, valga lo que valga B, el sustraendo, poniendo así a N en 1 para la próxima operación). Por tal motivo, A pasaría a valer 1 (Y NO 10, porque ya, supuestamente, le pasó al que le había pedido a él, vendría a ser el caso de los "999…" del medio en decimal o de los "111…" en binario visto antes. De acá, a vista humana, queda: 1 (A convertido) – 0 (B) = 1 (R) y pido 1 al próximo (N=1). Al igual que antes, hagámoslo ahora al estilo computadora, con acarreo y entradas: 1 (C) – 0 (A) – 0 (B) = 1 (C – A) – 0 (B) = 1 (R), con pedido para la próxima, o sea:
Con entrada C en 1, A en 0 y B en 0, tenemos R en 1 y N en 1
Y tenemos acá entonces la séptima combinación, la anteúltima.
Terminemos entonces con la octava, igual que antes, pero con B en 1
A en 0 y B en 1: 0-1 (con acarreo, C es 1) es 0 (R) y pide 1: N = 1
El tema de que esta operación termina pidiendo al próximo es exactamente igual al anterior, como ya vimos y dijimos que sucedería en el séptimo caso, por lo que no lo volveremos a explicar. Así que veamos la resta en si nomás. Tenemos: 1 (A convertido) – 1 (B) = 0 (R) y pido 1 al próximo (N=1). Como siempre, hagámoslo ahora al estilo computadora, con acarreo y entradas: 1 (C) – 0 (A) – 1 (B) = 1 (C – A) – 1 (B) = 0 (R), con pedido al próximo, o sea:
Con entrada C en 1, A en 0 y B en 1, tenemos R en 0 y N en 1
Y así, POR FIN, tenemos las ocho combinaciones entre entradas A y B y un acarreo (C), que resumiremos en el siguiente cuadro, que es el que usa la ALU para la resta:
|
C |
A |
B |
R |
N |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
O sea, todo lo anterior para decir que a la compu se le dijo que haga esto, y eso hace, sin razonar nada…
Aquí, la bandera de la resta es la N (NEGATIVE), que se activa cuando "pido" uno a la resta siguiente, o se apaga, cuando nada pido. El acarreo de la próxima operación C toma el valor 1 si esta bandera está prendida, o 0 si está apagada.
Circuitos Lógicos.
Vamos a tener en cuenta para lo que sigue a la suma y a la resta, ya que la computadora, y la electrónica, más que nada se manejan con compuertas lógicas y, en base a ellas, o a combinaciones de ellas, hacer distintas operaciones.
En otras palabras, sólo tenemos para hacer OR, XOR, AND y NOT, pero no tenemos
Cómo hacer directamente una suma o una resta, ni sus banderas de salida (las de entrada las toman en base a las de la salida anterior, as que no hay que "hacerla").
La parte fácil: si vemos las tablas lógicas, tanto la de la suma como la de la resta, veremos que siempre que SOLO UNA de las variables de entrada esté en 1, o LAS TRES a la vez estén en 1, la respuesta R es 1, caso contrario, la respuesta es 0. No les parece conocido a la extensión del X-OR, con el tema de la imparidad? Bueno, pues es exactamente eso. Siempre que la cantidad de entradas en 1 entre A, B y C sea impar (O CADA UNA SOLA O LAS TRES A LA VEZ), R vale 1, sino (de a dos valen 1 o todas valen 0), la salida R vale 0.
Pero para el análisis de la parte lógica, en lo que nos tenemos que fijar MÁS es en las salidas 1, en las respuestas Verdaderas, ya que, como dijimos, si no cumplo algo de lo que está adelante, no es obligación NO CUPLIR con la respuesta. Se entiende? Recuerdan de la parte de proposiciones lógicas: Si llueve y hace frío entonces salgo con campera… pero… y si no llueve ni hace frío? Eso me implica que tengo que salir SIN campera? NO. Por eso, lo que más importa es la salida en 1, que son las que se analizan.
Ya tenemos cómo obtener las R de la suma y de la resta, con un par de compuertas X-OR una tras otra (por ejemplo, A con B y el resultado con C) o una compuerta X-OR de tres entradas, y ponemos a A, B y C en cada entrada.
Ahora nos queda ver el comportamiento de V (OVERFLOW) y de N (NEGATIVE) en cada caso. Para esto vamos a utilizar un poco de razonamiento y otro de lógica electrónica. El objetivo acá es saber qué salidas (tanto del V como del N) tengo positivas (en 1). Separemos entonces estos casos, veamos cuántos son, y cómo podríamos llegar a esos resultados utilizando solamente las compuertas lógicas que ya conocemos. Sacaremos entonces de la tabla de verdad solamente aquellas condiciones en las V o R es 1, y veremos qué condiciones deben cumplir las entradas para que esto sea así, SIN IMPORTARME PARA ESTO qué Resultado (R) me había dado la operación (al menos para la lógica electrónica, pero nos importa para el razonamiento nuestro, el humano.
Comencemos con el OVERFLOW (V). Saquemos lo dicho (sólo V = 1) de la tabla de la suma:
|
C |
A |
B |
V |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
Ahora, usando un poco de razonamiento lógico, podemos decir que si tanto A vale 1 y B vale 1, 1 + 1 (binario) es 10 (binario), sin importar el valor de C. Este caso puede darse con la combinación de A y C, o de B y C también, pero como tenemos que hacer comparaciones de a 2, tomaremos las dos variables de entrada: A y B
Agrupamos entonces (solamente invertimos el orden de la 2da y 3ra fila):
|
C |
A |
B |
V |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
· a) Entonces, con las dos primeras filas podemos preguntar si A AND B son 1, no me importa lo que C valga (como verán en estas dos filas, C en la primera vale 0 y en la segunda vale 1, así que no me importa su comportamiento, su valor), entonces V va a valer 1. Esto es lógico ya que 1 + 1 queda ya en 10, o sea que me voy a llevar 1 sí o sí, valga lo que valga C (si valiese 0, queda en 10 y si valiese 1, queda en 11)
· b) Descartamos entonces (momentáneamente) las dos primeras filas y veamos las dos que siguen: Veremos que si A es 1 O B es 1 y a la vez que se cumplen esas dos condiciones, C vale 1, que serían los casos que quedan para juntar a C Y A y a C Y B, entonces la salida es verdadera. Cómo el A Y B en 1 con C en 1 se cumple en la segunda fila, y ya la tenemos, acotemos entonces el O a un O-exclusivo, teniendo así: (A XOR B) es 1 AND C es 1, entonces nuestra salida V vale 1.
Juntamos así estas dos condiciones, y las unimos con un OR: SI se cumple que (A AND B son 1) OR se cumple que ((A XOR B) es 1 AND C es 1) entonces la salida V será 1
Del mismo modo veremos la resta. Saquemos lo que nos interesa:
|
C |
A |
B |
N |
|
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
Agrupemos a conveniencia (ya veremos la conveniencia) alternando columnas (la C):
|
A |
B |
C |
N |
|
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
Y luego filas (2da y 3ra)
|
A |
B |
C |
N |
|
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
· a) veamos la 3ra y 4ta fila, que me dicen que si B AND C son 1, sin importarme lo que A valga, la salida N va a valer 1. Esto quiere decir que si alguien me pedía 1 (C = 1) y B vale 1, no importa lo que valga A, voy a terminar pidiendo otra vez, porque si A valiese 1, este se lo daría al que le pidió y quedaría en 0 y no podría restarle al 1 que ya vale B, y así tendría que pedir, y, peor aún, si A valiese 0 y B valiese 1 y encima le están pidiendo (C = 1), sí o sí va a tener que pedir.
· b) Veamos las dos primeras columnas. Acá lamentablemente hay que complicarla más. Es similar a las últimas dos analizadas con la suma, con un XOR pero entre B y C, y a esto hay que decirle: "siempre y cuando A valga 0". Pensemos primero qué pasa acá: decimos que si A vale 0 y, o bien B vale 1 o bien me están pidiendo (descartamos otra vez el "los dos a la vez valen 1" porque ya lo tenemos en la condición anterior) queda mas que claro que vamos a tener que pedir, porque A no puede dar a quien le pide aunque B valga 0 (C = 1 y B = 0), como tampoco A valiendo 0, puedo restarle un B valiendo 1, por más que nadie pida (en este caso: B = 1 y C = 0). Hasta acá quedamos claros. Pero yo no puedo hacer una comparación lógica con un "algo = 0", todas las comparaciones se hacen con un "algo verdadero", con un "algo = 1". Entonces aparece nuestro conocido amigo NOT, el inversor, e invertimos acá el valor de A para ponerlo en 1 en vez de 0, y nos queda entonces: (B XOR C) es 1 AND NOT(A) es 1, entonces la salida R vale 1.
Juntamos otra vez las dos condiciones, uniéndolas también con un OR: SI se cumple que (B AND C son 1) OR se cumple que ((B XOR C) es 1 AND NOT(A) es 1) entonces la salida R será 1.
Ahora veamos estas compuertas lógicas, cómo se representan con sus respectivos gráficos:
En las compuertas, como verán, hay dos "palitos" al costado izquierdo y un "palito" al costado derecho. Estos vienen a representar las entradas y la salida respectivamente de cada compuerta. Es la forma de representarlos y gráficamente se dibujan sobre el chip mismo que tiene estas compuertas estos esquemas, poniendo las entradas en las patas donde debemos poner los cables con las entradas y en la patita de la salida, la salida. Habitualmente estos chips en donde están los circuitos tienen 7 patitas de cada lado, son rectangulares finitos con dos lados largos y dos cortitos. Sobre los largos están estas 7 patitas, dando un total de 14 patitas. En uno de los lados chiquitos hay una muesca; esta muesca me dice que su pata más próxima del lado izquierdo es la número 1, así no nos equivocamos al poner los cables, pudiendo dañar al chip. Cada integrado que posee las compuertas XOR, OR o AND tiene cuatro adentro, y las que tienen la negación tiene seis. Así, en las primeras, tenemos 3 patas por cada una de las 4 compuertas y dan un total de 12 patitas y en las NOT, son 2 patas por cada una de las 6 compuertas, dando un total de 12 patitas también. Como todo componente electrónico, necesita energía para hacerlo andar, así que en las dos que sobran (dijimos que eran 2 filas de 7 para cada una, 14 patitas en total), van: en una la masa o tierra (en la última de la fila de la izquierda, debajo de todo, poniendo la muesca para arriba), y en la otra la alimentación (la primera de la derecha, al lado de la muesca). En un chip de estos, de 14 patas, serían la para 7 y la pata 14 respectivamente.
Veamos como representamos algo entonces: Tenemos las entradas de las variables A y B y obtenemos una respuesta R. Para esto si ingresaremos una entrada positiva en la pata que representaría a la variable A, dándole 5Voltios o ingresamos una entrada positiva en la pata que representaría a la variable B (pero no las dos a la vez), tendríamos una salida similar a esas entradas (5V) en la pata R que representa la salida. Gráficamente:
Combinando salidas con entradas en estos chips, podemos hacer las combinaciones que queramos, para obtener los resultados que deseemos. Así, por ejemplo, si yo sé que la suma la logramos haciendo un XOR entre las variables de entrada A y B, y a ese resultado le aplicamos OTRO XOR con la variable de entrada C (el acarreo), podríamos graficarlo de la siguiente manera:
Y así, en la variable de salida R (final) podemos tener el resultado de la suma binaria dependiendo de los valores que tengan cada una de las variables de entrada A, B y C.
Con esta misma combinación, podemos interpretar la resta, ya que, como vimos, es el mismo resultado, sólo que con la resta tomamos en la variable de entrada C, el valor que tenga la bandera N
Y un poco más complicado para las banderas. Por ejemplo, con la resta (más difícil). Claramente veremos los dos bloques, los puntos a) con B AND C y b) con (B XOR C) AND NOT(A), ambos dos unidos con un OR, o sea, que sale positivo (se enciende la bandera N) si en cualquiera de los dos casos (a o b) tuviese una respuesta positiva:
Similar es el gráfico de la bandera de la suma: a) A AND B y b) (A XOR B) AND C también unidos con un OR:
Todo esto lo tenemos que juntar para hacer el diagrama lógico, y luego pasar eso directamente a los circuitos integrados.
Para la parte de las comparaciones lógicas, con una compuerta de cada chip que posea esa compuerta en particular, ya alcanza. Pero para la suma y para la resta, debemos armar el circuito para ver como terminamos uniendo las entradas con las salidas, en el circuito final, por medio de cables.
Dado que por cada chip (circuito integrado) tenemos sólo cuatro compuertas iguales de la operación lógica que realice ese chip en particular, llegamos justo a utilizar solamente un chip de cada tipo de compuertas. El chip con cuatro compuertas, es llamado 74xxNN, donde xx es el tipo de chip, en nuestro caso en particular usaremos o LS (que son rápidos y utilizan sólo entradas de 5V) o HC (rápidos, pero con un rango de entradas mas amplio, entre 3V y 6V) y NN son dos (o tres) números que nos dice el tipo de compuerta que tiene ese chip.
Veamos entonces. Comencemos viendo cuántos XOR tenemos:
· 1) A XOR B (de la operación lógica XOR en sí)
· 2) A XOR B (de la primera parte de la suma)
· 3) A XOR B (del punto b de la bandera de la suma)
· 4) B XOR C (del punto b de la resta)
· 5) Salida de A XOR B junto con el acarreo C de la suma, para el resultado de la suma
· 6) Salida de B XOR C (acarreo de la resta) junto con A, para el resultado de la resta
Agrupándolos entonces nos quedan sólo 4, ya que los tres primeros son exactamente lo mismo, y no vale la pena utilizar distintas compuertas para obtener el mismo resultado con las mismas entradas.
Sigamos con cantidad de AND:
· 1) A AND B (de la operación lógica AND en sí)
· 2) A AND B (del punto a de la bandera de la suma)
· 3) B AND C (del punto a de la bandera de la resta)
· 4) Junto A XOR B con C con un AND en el punto b de la bandera de la suma
· 5) Junto B XOR C con -A con un AND en el punto b de la bandera de la resta
Los dos primeros son lo mismo, así que me quedan 4 también.
Seguimos con OR:
· 1) A OR B (de la operación lógica OR en sí)
· 2) La unión final de las dos partes en la bandera de la suma
· 3) La unión final de las dos partes en la bandera de la resta
Y no tenemos más. Acá sólo usaremos 3 de las 4 compuertas.
Ahora NOT: Por ahora sólo la tenemos para negar a la variable A en la bandera de la resta, en un ratito vamos a utilizar dos más.
Conozcamos ahora otro chip, de la misma familia de los TTL, pero este no posee compuertas lógicas, sino un circuiterío especial llamado multiplexor. La función del multiplexor es, teniendo unas cuantas entradas, sólo una salida y una forma se seleccionar, elige entonces el dato de qué entrada quiero en la salida. Así, pondremos por medio de cablecitos: en una entrada: la salida de la compuerta A XOR B, en otra: la salida de la compuerta A AND B, en otra: la salida de la compuerta A OR B, en otra, la salida de las suma entre A, B y el C de la suma y en otra: la salida de las restas entre A, B y el C de la resta. Ocuparemos así 5 de las 8 entradas que tiene este chip.
La forma que tiene para seleccionar es por medio de una combinación de 3 patas llaves especiales de entrada. Combinando entre las 3 (poniendo 5V en algunas y las otras sin carga), podemos elegir el valor de cuál de las 8 entradas queremos ver en la salida, ya que puedo hacer 2 (posibilidades en cada pata: hay o no hay voltaje) al cubo (son 3 llaves) igual a 8. Esto digamos que es el "control" que haríamos sobre la ALU. Todas las operaciones se hacen ni bien entran A y B y las banderas activan los acarreadores, entonces yo como "controlador" debo decidir cuál de todas es la que necesito como respuesta de salida. Digamos que seríamos nosotros la "unidad de control" de la CPU, los que le vamos a dar los valores de A, de B y qué operación tiene que realizar.
Utilizaremos un sexto circuito en nuestro proyecto, que es un chip que tiene dos compuertas AND de cuatro entradas cada una, o sea, obtengo una salida positiva siempre y cuando TODAS las entradas (las 4) estén en 1 (tengan voltaje). A este circuito lo vamos a utilizar para que el resultado de las banderas salga cuando debe salir, dependiendo de la operación que estemos realizando con el multiplexor. Si estoy diciendo que quiero el resultado de la compuerta AND, y A y B están en 1, la salida correctamente estará en 1, pero A + B es 10, tendría un overflow (V) y esta bandera saldría activada, a menos que usemos este circuito para decirle: salí activada, siempre y cuando estés activada, pero esté siendo utilizada la operación que corresponde (en una suma en este caso, y no en un AND). Esta "operación que corresponde" la dan las 3 llaves que controlan el multiplexor, así que da ahí mismo las sacaremos.
Entonces, si para decir que la suma la tengo cuando tengo la combinación de las llaves 1 y 3 prendidas y la llave 2 apagada, y la resta la tengo cuando tengo la combinación de las llaves 2 y 3 prendidas y la llave 1 apagada. Conecto entonces con cablecitos en cada una de las 4 entradas: para la suma: la salida en sí de la bandera de overflow, la llave 1 y la llave 3. Todavía queda poner "algo" en la 4ta pata de esta compuerta. Ya vamos a ver que va ahí. Por ahora pasemos momentáneamente a la resta, y hacemos lo mismo: en una de las cuatro patas de entrada de la OTRA compuerta AND de este chip, pondremos a la salida en sí de la bandera de negative, la llave 2 y la llave 3. Y también me queda libre una pata acá, que también tenemos que ocupar.
Dado que para activar la salida de una compuerta AND de la cantidad de entradas que sean, TODAS sus entradas deben estar encendidas, y la condición para que sea, por ejemplo, una "suma" lo que esté trabajando, y eso lo digo con que la llave 1 esté prendida, la llave 3 esté prendida y la llave 2 esté apagada, entonces lo más fácil por hacer sería sacar un cablecito de la llave 2, llevarla al chip que tiene las puertas NOT (donde usé solo una de las seis que tiene), invertirla, y el resultado este, llevarlo a la cuarta pata que me quedaba libre del chip, del lado de la suma. Así, si la llave 2 estaba apagada, al pasarla por el inversor la enciendo, y va encendida a la compuerta AND "grande". Del mismo modo hacemos con la llave 1 en la resta, en otra compuerta inversora y a la pata que faltaba en el AND "grande", pero del lado de la resta.
Un punto extra, no realizado en este proyecto, es agregarle un par de circuitos más, los 74LS367, y conectar a la computadora, y, en vez de hacer a mano y ver en leds como en el video, controlar todo y ver los resultados con alguna interfaz con algún lenguaje de programación (visual Fox o visual Basic sirven recontra bien). Estos TTL extras son para proteger a la computadora de no meter la pata con los conectores de afuera, corriendo el riesgo de quemarla.
Para hacerlo, tendremos que usar el puerto paralelo. Por el "bus de datos" del mismo pasaremos las variables A, B, C de la suma y C de la resta. Se utilizará para esto el puerto 378h (888d) y los pines físicos del 2 al 5 (D0 a D3). Por el "bus de estado" pueden volver los resultados: R, N (negative) y V (overflow). Se usa el puerto 379h (889d) y los pines físicos 10, 12 y 13. Tendríamos que utilizar también el "bus de control" del puerto para activar las llaves "de control", utilizando el puerto 37Ah (890d) y los pines físicos 14, 16 y 17. El programa me queda como tarea pendiente.
Interpretando un poco el párrafo anterior, podemos ver cómo trabajarían en conjunto los tres buses principales de la computadora. Datos de entrada, estados de salida y algo que controle la situación.
Los circuitos utilizados son:
· 1) 74LS86: 4 XOR doble entrada
· 2) 74LS08: 4 AND doble entrada
· 3) 74LS32: 4 OR doble entrada
· 4) 74LS04: 6 NOT
· 5) 74LS21: 2 AND cuádruple entrada
· 6) 74LS151: un multiplexor de 8 entradas.
Todo esto se construirá sobre un protoboard, o placa experimental, en donde podemos poner los circuitos en el medio de la misma, y a sus costados (sobre la misma línea) poner los cables para unir entre las patas de los distintos circuitos. Se pondrán los 6 circuitos uno debajo del otro, en el mismo orden detallado arriba, y se interconectarán como se ve en el gráfico del final por medio de cables monofilares (desarmen un cable de red).
Al circuito lo alimentaremos con una fuente de 7,5V para luego bajarla y regularla con un circuito especial que mantiene 5V de salida, un 7805.
Las entradas de las variables A, B, C de suma y C de resta, las daremos con un switch cuádruple, conectado la entrada a 5V. Las llaves para la selección de la operación a realizar, las activaremos mediante conexión directa de cablecitos. Todas las salidas las monitorearemos con leds (diodos emisores de luz) de distintos colores, para distinguir entre cada una: las salidas de las operaciones serán en rojo, las banderas en amarillo y la salida general del multiplexor en verde.
Las resistencias que dan el 0 lógico a las entradas de las compuertas son de 820 o de 1000 ohmios, y las que prenden los leds son de 150 ohmios. No concierne al trabajo esta parte de la construcción, para qué sirven el resto de los componentes, sólo doy los valores para aquel que quiera intentar hacer algo. Estas resistencias van entre las entradas y masa. Los switches y las llaves cierran las conexiones con los 5V.
Aquí les dejo las páginas en donde están los dos videos del funcionamiento del proyecto:
Parte 1: Introducción y operaciones lógicas
http://www.youtube.com/watch?v=KjEb__iPR0c
Parte 2: Operaciones aritméticas: Suma y Resta http://www.youtube.com/watch?v=MrF0ByDcMl8
Y acá está el diagrama general del proyecto:
edu13...@gmail.com
FUNCIONAMIENTO DE UNA ALU (74181)
El 74181 es una unidad aritmético lógica bit slice implementada como un circuito integrado TTL de la serie 7400 de mediana escala de integración (MSI), conteniendo el equivalente de 75 puertas lógicas y comúnmente empaquetado en un DIP de 24 pines. La ALU de 4 bits de ancho puede realizar todas las operaciones tradicionales de suma, resta, decrementar, con o sin acarreo, al igual que operaciones lógicas AND, NAND, OR, XOR y SHIFT. Están disponibles muchas variaciones de estas funciones básicas, para un total de 16 operaciones aritméticas y 16 operaciones lógicas en dos palabras de cuatro bits. Las funciones de multiplicación y división no son proporcionadas, pero pueden ser realizadas en pasos múltiples usando funciones de SHIFT y suma o resta. SHIFT no es una función explícita pero puede ser derivada de varias funciones disponibles, incluyendo (A+B) más A, A más AB.
El 74181 realiza estas operaciones en dos operandos de cuatro bits que generan un resultado de cuatro bits con un acarreo en 22 nanosegundos. El 74S181 realiza las mismas operaciones en 11 nanosegundos, mientras que el 74F181 realiza las operaciones en típicamente 7 nanosegundos.
Múltiples 'slices' pueden ser combinados para tamaños arbitrariamente grandes de palabras. Por ejemplo, seis 74S181s y cinco generadores de acarreo look ahead 74S182 pueden ser combinados para realizar las mismas operaciones en operandos 64 bits en 28 nanosegundos. Aunque fue eclipsado por el desempeño de los microprocesadores de 64 bits de multi gigahertz de hoy, esto fue absolutamente impresionante cuando comparaba a las velocidades de reloj de submegahertz de los tempranos microprocesadores de cuatro y ocho bits.
El 74181 permitió que un CPU entero y en algunos casos, un computador entero pudiera ser construido en una sola tarjeta de circuitos impresos grande. El 74181 ocupa una etapa históricamente significativa entre los CPU más viejos basados en funciones de lógica discreta extendiéndose sobre múltiples tarjetas de circuitos y los microprocesadores modernos que incorporan todas las funciones del CPU en un solo componente. El 74181 fue usado en varios minicomputadores y otros dispositivos comenzando a finales de los años sesenta, pero a medida que los microprocesadores llegaron a ser más poderosos la práctica de hacer un CPU de componentes discretos cayó en favor, y el 74181 no fue usado en ningún nuevo diseño.
EDWARD MONTOYA OSORIO 3"B"
Gutierrez Gutarra Georges
¿Cómo funciona una ALU 74181? Explicar.
El 74181 es una unidad aritmético lógica (ALU) implementada como un circuito integrado TTL
FUNCIONAMIENTO:
El SN54 / 74LS181 es
una aritmética paralela de alta velocidad de 4 bits
Unidad Lógica (ALU). Controlado por las cuatro entradas
de selección de función
(S0... S3) y la entrada de control de modo (M).
Este circuito integrado tiene como entradas:
· Los cuatro bits del operando A.
· Los cuatro bits del operando B.
· Entradas de selección (para seleccionar la operación a realizar, entre 16).
· Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
· Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Con el 74181
se puede realizar todo las 16 posibles operaciones
lógicas o aritméticas.
Cuando la entrada de control del modo es BAJO, los
acarreos están habilitados y el dispositivo realiza operaciones
aritméticas sobre las dos palabras de 4 bits.
· La salida A = B del LS181 pasa a ALTO cuando los cuatro F salidas son altas y se pueden utilizar para indicar la lógica equivalencia más de cuatro bits cuando la unidad está en la resta de modo.
· La salida A = B es de colector abierto y puede ser cable-Y con otras salidas A = B para dar una comparación para más de cuatro bits. La señal A = B también se puede utilizar con el Cn + 4 señales para indicar una> B y A <B.
· La tabla de funciones enumera las operaciones aritméticas que son lleva a cabo sin un acarreo en. Un acarreo entrante agrega un uno a cada operación. Por lo tanto, seleccione código LHHL genera A menos B menos 1 (2s notación complemento) sin un equipaje en y A menos B genera cuando se aplica un acarreo.
· la resta es efectuado por adición complementaria (1s complementan)R, a llevar a cabo mediante préstamos; por lo tanto es un acarreo generada cuando no hay flujo inferior y no es carry genera cuando existe flujo inferior.
·
Como
se indica, el LS181 se puede utilizar con cualquiera de
nivel activo BAJO
insumos que producen salidas LOW activos o con activos
de alta insumos que producen salidas ALTAS activos. Para ambos
casos, el tabla enumera las operaciones que se realizan a los operando
marcado en el interior del símbolo lógico.
Alumno : Gutierrez Gutarra Georges / 3ero B
Peggy Quispe Tucto
-
paulantony...@gmail.com
Funcionamiento de un ALU 74181
La ALU puede programarse para que opere tanto en activa en alta como activa en baja.
En esta asignatura todos los circuitos los diseñamos y usamos considerando activa en alta porque nos parece la forma de trabajo más intuitiva.
La tabla de verdad de la ALU que aparece en el texto base es correcta y se corresponde con la que proporciona Texas Instruments y cuya hoja de característica se adjunta con este documento.
El problema está en que las tablas de verdad del funcionamiento que proporcionan los distintos fabricantes dependen de la interpretación de las señales, pero las señales de entrada y salida a la ALU son las que le entran y salen al circuito, sólo que se interpretan de una forma u otra dependiendo de si se considera activa en alta o en baja.
La tabla siguiente (proporcionada por el fabricante) muestra la forma en la que se pueden interpretar dichas señales en función de si se considera activa en alta o en baja.
Observen que las señales de activa
en baja son negadas respecto de las de activa en alta.
Como hemos dicho anteriormente, nosotros vamos a trabajar en activa en alta tanto en los diseños como en las simulaciones. Por tanto, para activa en alta, tanto las palabras de entrada, A3 A2 A1 A0 y
B3 B2 B1 B0, como las señales de control, S3 S2 S1 S0, M, Cn
, las interpretamos tal cual, o sea, son directamente (sin negar) los datos que salen de los generadores de pulsos y que entran en la ALU y quese corresponden con la cabecera de la tabla de verdad de la ALU para activa en alta. Estos serán los valores sobre los que deberemos operar a la hora de comprobar el funcionamiento de dicha ALU. Observen que las únicas señales que aparecen negadas son los acarreos o arrastres de entrada y salida,Cn y Cn+4.El significado de Cn en la tabla de verdad (de activa en alta, la del texto) es: Cn
=H (sin Acarreo). Por tanto, su significado es Cn
= 0. O sea, Acarreo = 0
Cn =L (con Acarreo). Por tanto, su significado es Cn
= 1. O sea, Acarreo = 1
Si miramos la página 3-712 de las hojas de características adjuntas verán que esta señal está negada, esta es la razón por la que a este terminal lo nombran con Cn
. De nuevo, nosotros en el terminal marcado con Cn ponemos directamente la señal, sin negarla. Es decir, a la ALU no hay que añadirle ningún inversor. Se programa directamente con las señales tal cual y se interpretan también tal cual (salvo Cn+4, como veremos más adelante). Así, si queremos programar la ALU para que realice la función aritmética sin acarreo “A PLUS B” deberemos poner los siguientes valores a las señales de control:
S3 S2 S1 S0 = H L L H, M = L, terminal Cn
(olvidaros del negado) = H.
Si por el contrario, queremos que realice la operación “A PLUS B PLUS 1” deberemos poner:
S3 S2 S1 S0 = H L L H, M = L, terminal Cn (olvidaros del negado) = L.
º
Kleisvit Nestor Alva Rojas
¿ Cómo funciona una ALU 74181? | |
Se trata de un circuito integrado con la capacidad de realizar diferentes operaciones aritméticas y lógicas (es decir, del álgebra de Boole), con dos palabras de n bits Se pueden encontrar como circuitos independientes, y también como bloque funcional dentro de los microprocesadores y microcontroladores.
En general, las operaciones matemáticas están codificadas en binario natural y en complemento a 2 para las restas, pero se pueden codificar en otros códigos, como por ejemplo BCD natural.
El más conocido es 74LS181, que es una ALU de 4 bits, que puede realizar hasta 32 funciones diferentes (16 lógicas y 16 aritméticas), trabaja con números binarios de 4 bits, aunque se pueden conectar en cascada para aumentar el número de bits. Este circuito integrado tiene como entradas:
- Los cuatro bits del operando A.
- Los cuatro bits del operando B.
- Entradas de selección (para seleccionar la operación a realizar, entre 16).
- Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
- Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Como salidas tiene los 4 bits del resultado, más una salida comparador (A = B) y salidas de acarreo.
La ALU puede programarse para que opere tanto en activa en alta como activa en baja.
En esta asignatura todos los circuitos los diseñamos y usamos considerando activa en alta porque nos
parece la forma de trabajo más intuitiva.
La tabla de verdad de la ALU que aparece en el texto base es correcta y se corresponde con la que
proporciona Texas Instruments y cuya hoja de característica se adjunta con este documento.
El problema está en que las tablas de verdad del funcionamiento que proporcionan los distintos
fabricantes dependen de la interpretación de las señales, pero las señales de entrada y salida a la ALU
son las que le entran y salen al circuito, sólo que se interpretan de una forma u otra dependiendo de si
se considera activa en alta o en baja.
La tabla siguiente (proporcionada por el fabricante) muestra la forma en la que se pueden interpretar
dichas señales en función de si se considera activa en alta o en baja.
Alumno: Alva Rojas Néstor 3 "A"
JOHN CASTRO ALLAIN
¿ Cómo funciona una ALU 74181?
El 74181 funciona para realizar todas las operaciones tradicionales de suma, resta, decrementar, con o sin acarreo, al igual que operaciones lógicas AND, NAND, OR, XOR y SHIFT. Están disponibles muchas variaciones de estas funciones básicas, para un total de 16 operaciones aritméticas y 16 operaciones lógicas en dos palabras de cuatro bits. Las funciones de multiplicación y división no son proporcionadas, pero pueden ser realizadas en pasos múltiples usando funciones de SHIFT y suma o resta. SHIFT no es una función explícita pero puede ser derivada de varias funciones disponibles, incluyendo (A+B) más A, A más AB.
El 74181 realiza estas operaciones en dos operandos de cuatro bits que generan un resultado de cuatro bits con un acarreo en 22 nanosegundos. El 74S181 realiza las mismas operaciones en 11 nanosegundos, mientras que el 74F181 realiza las operaciones en típicamente 7 nanosegundos.
- Los cuatro bits del operando A.
- Los cuatro bits del operando B.
- Entradas de selección (para seleccionar la operación a realizar, entre 16).
- Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
- Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
pariona.del...@gmail.com
El 74181 es una unidad aritmético lógica bit slice implementada como un circuito integrado TTL de la serie 7400. ALU son las siglas de Aritmethic Logic Unit, es decir, Unidad Lógico Aritmética.
Se trata de un circuito integrado con la capacidad de realizar diferentes operaciones aritméticas y lógicas (es decir, del álgebra de Boole), con dos palabras de n bits Se pueden encontrar como circuitos independientes, y también como bloque funcional dentro de los microprocesadores y microcontroladores.
El 74LS181, que es una ALU de 4 bits, que puede realizar hasta 32 funciones diferentes (16 lógicas y 16 aritméticas), trabaja con números binarios de 4 bits, aunque se pueden conectar en cascada para aumentar el número de bits. Este circuito integrado tiene como entradas:
- Los cuatro bits del operando A.
- Los cuatro bits del operando B.
- Entradas de selección (para seleccionar la operación a realizar, entre 16).
- Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
- Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Como salidas tiene los 4 bits del resultado, más una salida comparador (A = B) y salidas de acarreo.
Como curiosidad decir que este circuito integrado trabaja con lógica inversa en las entradas de datos y en las salidas, es decir, que para estos pines se invierte el significado de los 1 y los 0. Aunque es posible hacerlo trabajar con lógica directa.
Configuración de pines del CI 74LS181
Tabla con las funciones que pueden realizarse con el 74LS181
ALUMNO: PARIONA DE LA CRUZ JUNIOR 3º "A"
Jhonny Cristian Gonzales Andia ............3 "B"
¿ Cómo funciona una ALU 74181? | |
El 74181 realiza estas operaciones en dos operandos de cuatro bits que generan un resultado de cuatro bits con un acarreo en 22 nanosegundos. El 74S181 realiza las mismas operaciones en 11 nanosegundos, mientras que el 74F181 realiza las operaciones en típicamente 7 nanosegundos.
Múltiples 'slices' pueden ser combinados para tamaños arbitrariamente grandes de palabras. Por ejemplo, seis 74S181s y cinco generadores de acarreo look ahead 74S182 pueden ser combinados para realizar las mismas operaciones en operandos 64 bits en 28 nanosegundos. Aunque fue eclipsado por el desempeño de los microprocesadores de 64 bits de multi gigahertz de hoy, esto fue absolutamente impresionante cuando comparaba a las velocidades de reloj de submegahertz de los tempranos microprocesadores de cuatro y ocho bits.
El 74LS181 consta de:
- Cuatro entradas para el operando A.
- Cuatro entradas para el operando B.
- Cuatro entradas de selección (S0 a S3) que determina cual función lógica o aritmética debe ser calculada.
- Una entrada de modo (M) que determina si la operación a ejecutarse será lógica o aritmética.
- Una entrada de acarreo (Cin).
- Cuatro líneas de salida para el resultado (F0 a F3).
- Una salida de acarreo (Cout).
- Una salida de comparación A=B.
La ALU puede ejecutar:
- 16 operaciones lógicas.
- 5 operaciones aritméticas.
- 8 operaciones combinadas aritméticas/lógicas.
yorda quiroz fuentes
¿COMO FUNCIONA UNA “ALU O AUL”? I.- INTRODUCCION
La unidad aritmética lógica (UAL o ALU) es el órgano operativo del
microprocesador puede realizar operaciones tanto aritméticas como lógicas entre
un par de operandos de N bits, se compone en dos módulos la unidad aritmética y
la unidad lógica. Para seleccionar la operación que se quiere realizar
normalmente estos dispositivos poseen unas entradas de selección.
En la arquitectura de un microprocesador observamos en la figura que este tiene
una unidad aritmética y lógica de 8 bits este opera con datos de 8 bits el cual
posee dos vías par el acceso de datos:
· Acceso directo desde el bus interno del microprocesador
· Acceso al acumulador con el cual trabaja habitualmente
Además tiene una comunicación con los diferentes bits de registro de estados. ESTRUCTURA Y FUNCIONAMIENTO DE UNA ALU
Todas
las operaciones aritméticas se llevan a cabo en la unidad aritmética lógica
ALU, En inglés ALU significa (Unidad
Aritmética Lógica).
El propósito general de la ALU es aceptar los
datos binarios que se almacenan en la memoria y ejecutar operaciones
aritméticas y lógicas con estos datos según las instrucciones de la unidad de
control. La unidad aritmética lógica contiene cuando menos dos registros de flip-flop:
el registró B y el registro acumulador. También contiene lógica combinatoria,
la cual realiza las operaciones aritméticas y lógicas con los números binarios que están
almacenados en el registro B y en el acumulador.
Una secuencia típica de operaciones puede ocurrir así:1. La unidad de control recibe una instrucción (de la unidad de memoria) especificando qué un número almacenado en una localidad de memoria particular (dirección) se sumara al número que esta almacenando en ese momento el registro acumulador.2. El número que se sumara se transfiere de la memoria al registro B.3. El número en el registro B y el número en el registro de acumulador se suman en los circuitos lógicos (mediante un comando desde la unidad de control). Luego la suma resultante se enuncia al acumulador para su almacenamiento.4. El nuevo número en el acumulador puede permanecer allí, de manera que se le pueda sumar otro número, o, si el proceso aritmético particular ha terminado, se puede transferir a la memoria para ser almacenado. ATTE: YORDAN WUILDER QUIROZ FUENTES
Miguel Arias
Las unidades aritmetico-logicas (ALU) constituyen dispositivos utiles y versatiles que implementan diferentes operaciones logicas y aritmeticas, generalmente en un solo circuito integrado.
Se trata de un circuito integrado con la capacidad de realizar diferentes operaciones aritméticas y lógicas (es decir, del álgebra de Boole), con dos palabras de n bits Se pueden encontrar como circuitos independientes, y también como bloque funcional dentro de los microprocesadores y microcontroladores.
En general, las operaciones matemáticas están codificadas en binario natural y en complemento a 2 para las restas, pero se pueden codificar en otros códigos, como por ejemplo BCD natural.
El más conocido es 74LS181, que es una ALU de 4 bits, que puede realizar hasta 32 funciones diferentes (16 lógicas y 16 aritméticas), trabaja con números binarios de 4 bits, aunque se pueden conectar en cascada para aumentar el número de bits. Este circuito integrado tiene como entradas:
- Los cuatro bits del operando A.
- Los cuatro bits del operando B.
- Entradas de selección (para seleccionar la operación a realizar, entre 16).
- Entrada de acarreo, por si viene de un integrado con el resultado de menor peso.
- Entrada de control, para seleccionar si la operación a realizar deber ser aritmética o lógica.
Funcionalmente, una unidad del tipo 74181 acepta como datos dos palabras de
cuatro bits A = A3A2A1A0 y B = B3B2B1B0, produciendo como resultado otra palabra
de 4 bits F = F3F2F1F0 (ver figura 3.17). Ademas de estas lıneas posee un acarreo de
entrada Cn y un acarreo de salida Cn+4, activos a nivel bajo.
La operaci´on que se realiza sobre estos datos esta determinada por las entradas de
seleccion S = S3S2S1S0 y la entrada de modo M. Cuando M = L las operaciones son
aritmeticas (suma, resta, etc.), mientras que cuando M = H las operaciones son logicas
(AND, OR, etc.). Los acarreos de entrada y de salida solo tienen sentido cuando se trata
de operaciones aritmeticas. La tabla 3.5 ilustra las distintas operaciones que se realizan
en terminos del valor de las entradas S y M.
La interpretacion de la operacion realizada depende del tipo de logica que se utilice:
positiva o negativa. En el caso de logica positiva se hacen corresponder los niveles de
tension H y L con los valores logicos H=1 y L=0. Se utiliza la tabla de la izquierda.
Sea por ejemplo S = HLLH, M = L, A = LHHL, B = LLHH y Cn = L. La operacion
a realizar esta determinada por M (L: operacion aritmetica) y S (HLLH: A plus B ´o A
plus B plus 1, sin acarreo y con acarreo, respectivamente). Al ser Cn = L (existe acarreo
de entrada) entonces la operacion que se realiza es F = A plus Bplus 1. Como la logica
es positiva A = 0110 (6) y B = 0011 (3), entonces F = 1010 = HLHL (10) y no existe
acarreo de salida, Cn+4 = H.
Importancia
Aunque el 74181 es solamente un ALU y no un microprocesador completo, simplificó grandemente el desarrollo y la fabricación de computadores y de otros dispositivos que requirieron cómputo de alta velocidad durante finales de los años 1960 hasta principio de los años 1980, y todavía es referido como un diseño "clásico" de ALU.2
Antes de la introducción del 74181, los CPU del computador ocuparon múltiples tarjetas de circuitos e incluso los computadores muy simples podían llenar múltiples gabinetes. El 74181 permitió que un CPU entero y en algunos casos, un computador entero pudiera ser construido en una sola tarjeta de circuitos impresos grande. El 74181 ocupa una etapa históricamente significativa entre los CPU más viejos basados en funciones de lógica discreta extendiéndose sobre múltiples tarjetas de circuitos y los microprocesadores modernos que incorporan todas las funciones del CPU en un solo componente. El 74181 fue usado en varios minicomputadores y otros dispositivos comenzando a finales de los años sesenta, pero a medida que los microprocesadores llegaron a ser más poderosos la práctica de hacer un CPU de componentes discretos cayó en favor, y el 74181 no fue usado en ningún nuevo diseño.
sofia.8....@gmail.com
Marcial Salazar Cayllaua
Unidad Aritmético Lógica 74LS181
UNIDAD ARITMÉTICO LÓGICA (ALU)
Una ALU es un sistema que permite realizar operaciones lógicas como OR, ANDA entre otras y operaciones aritméticas, por ejemplo, la suma, resta, etc. Dentro de las ALU comerciales se encuentra el IC 74LS181.
La función de cada uno de los pines de este IC, se describe a continuación:
Pines 2, 23, 21 y 19, respectivamente /A0 ... /A3, son las entradas de uno de los operandos, activos en BAJO.
Pines 1, 22,20 18, respectivamente / B0 ... /B3, entradas del los operandos restantes, activos en BAJO.
Pines 9, 10, 11 y 13, respectivamente /F0 ... /F3, son las salidas de la ALU, donde se tendrán los resultados de las entradas.
Pin 8 M , es una de las líneas de control; por medio de esta líneas se le indica al circuito la operación a realizar, Si M=1 realiza operaciones lógicas y realiza operaciones aritméticas si M=0.
Pin 7 Cn, es la entrada de acarreo esta entrada deberá ser 0 en operaciones aritméticas; en caso de ser un 1 habrá que sumarlo a la función aritmética que se seleccione.
Pin 14 A=B, es una salida de colector abierto e indica cuándo las cuatro salidas está a nivel ALTO. Si se selecciona la operación aritmética de la resta es salida se activará cuando ambos operandos sean iguales.
Pin 17 /G, salida de generación de acarreo. En operación aritmética de la suma, esta salida indica que la salida F es mayor o igual a 16, y en la resta F es menor que cero.
Pin 15 /P, salida de propagación de acarreo. En la operación aritmética de la suma, esta salida indica que F es mayor o igual a 15 y en la resta que F es menor que cero..
Las salidas /G y /P se utilizan par acoplar varios circuitos integrados del tipo 74181 en cascada empleando el método de propagación en paralelo.
Pin 16 Cn+4 es la salida de acarreo.
Pines 6, 5, 4 y 3, respectivamente So ... S3, son las líneas de control del circuito; mediante éstas se selecciona la función que ha de realizar el circuito.
Pin 24 = VCC
Pin 12 = GND


FUNCIONAMIENTO E IMPORTANCIA DE ALU 74181
El 74181 es una unidad aritmético lógica bit slice implementada como un circuito integrado TTL de la serie 7400 de mediana escala de integración (MSI), conteniendo el equivalente de 75 puertas lógicas y comúnmente empaquetado en un DIP de 24 pines. La ALU de 4 bits de ancho puede realizar todas las operaciones tradicionales de suma, resta, decrementar, con o sin acarreo, al igual que operaciones lógicas AND, NAND, OR, XOR y SHIFT. Están disponibles muchas variaciones de estas funciones básicas, para un total de 16 operaciones aritméticas y 16 operaciones lógicas en dos palabras de cuatro bits. Las funciones de multiplicación y división no son proporcionadas, pero pueden ser realizadas en pasos múltiples usando funciones de SHIFT y suma o resta. SHIFT no es una función explícita pero puede ser derivada de varias funciones disponibles, incluyendo (A+B) más A, A más AB
geacias 3er "B"
leone...@gmail.com
La ALU más conocida es la 74181, que es un circuito integrado que es capaz de realizar 16 operaciones lógicas y 16 operaciones aritméticas con dos palabras de 4 bits (A3 A2 A1 A0) y (B3 B2 B1 B0). Existe una entrada de control (M) para indicar si se va a efectuar una operación aritmética (M=L) o lógica (M=H) y otras 4 entradas de control (S3 S2 S1 S0) que determina la operación concreta según se especifica la tabla adjunta. La tabla es doble, una para entradas y salidas activas a nivel alto y la otra para entradas y salidas activas a nivel bajo.
Además existen otras entradas y salidas auxiliares como son, Cn y Cn+4 para la entrada y salida del acarreo de la suma, A=B para la comparación.
Tabla de Funciones para datos a nivel Alto
Programando adecuadamente las líneas de selección (S3S2S1S0) y la de modo (M) junto con la de acarreo previo (Cn), la ALU puede ejecutar 16 operaciones lógicas y 32 operaciones aritméticas diferentes con los datos A=A3A2A1A0 B=B3B2B1B0. Estas operaciones, con sus respectivos códigos de selección, se relacionan en la siguiente tabla. Se consideran tanto las entradas como las salidas son activas en alto. Para programar el dispositivo como generador de funciones lógicas, la entrada selectora de modo (M) debe estar a nivel alto. La operación lógica deseada se programa mediante un código de 4 bits de la forma S3S2S1S0 aplicado a las entradas selectoras de función. El estado de Cn es indiferente.
Por ejemplo, para realizar la operación lógica A XOR B, si A= 1011 y B = 0001, la línea M debe estar en 1 lógico y las líneas S3S2S1S0 deben tener el código 0110.
Cada bit de la palabra de salida F = F3F2F1F0 es el resultado de la operación XOR de cada bit de la palabra A con el correspondiente bit de la palabra B. Es decir, F3 =A3 XOR B3, F2 = A2 XOR B2y así sucesivamente. Por tanto, F = 1010.
Para programar la ALU como generadora de funciones aritméticas, la línea M debe llevarse a nivel bajo con el fin de habilitar los acarreos internos. La suma de A y B, por ejemplo, se realiza cuando el código de las entradas de selección de función es 1001. La entrada de acarreo Cn es activa en bajo.
Si la suma produce un acarreo de salida (Cn+4) igual a 1, esté también será activo en bajo. La ALU utiliza un sistema interno de generación de acarreos conocido como carry look ahead (acarreo anticipado), que no requiere que la suma sea calculada en su totalidad antes de establecer la naturaleza del acarreo resultante.
Luis Enrrique Llaja Pisco
Unidad Aritmético Lógica 74LS181
UNIDAD ARITMÉTICO LÓGICA (ALU)
FUNCIONES ARITMÉTICASY LOGICAS.-
FUNCIONAMIENTO :
· B3:B2:B1:B0 entradas del segundo operando,
· S3:S2:S1:S0 selectores de función: mediante éstas se selecciona la función que ha de realizar el circuito (suma, resta, multiplicación, etc.)
· F3:F2:F1:F0 salidas de la ALU, donde se tendrán los resultados.
· M: selector de Modo: sirve para determinar la operación a realizar, Si M=1 realiza operaciones lógicas y realiza operaciones aritméticas si M=0.
· Cn: entrada de acarreo activa en nivel bajo.
· A=B: es una salida de colector abierto e indica cuándo las cuatro salidas están a nivel ALTO. Si se selecciona la operación aritmética de la resta, esta salida se activará cuando ambos operandos son iguales.
· G: acarreo de generación. En operación aritmética de la suma, esta salida indica que la salida F es mayor o igual a 16, y en la resta F es menor que cero.
· P: acarreo de propagación. En la operación aritmética de la suma, esta salida indica que F es mayor o igual a 15 y en la resta que F es menor que cero.
· G y P se utilizan para acoplar varios circuitos integrados del tipo 74181 en cascada empleando el método de propagación en paralelo.
· Cn+4 es el acarreo de salida.
sebastianescu...@gmail.com
El 74181 es una unidad aritmético lógica bit slice implementada como un circuito integrado TTL de la serie 7400. Fue la primera ALU completa en un simple chip.1 Fue utilizado como el núcleo aritmético/lógico en los CPU de muchos minicomputadores históricamente significativos y en otros dispositivos.
El 74181 es un circuito integrado TTL de la serie 7400 de mediana escala de integración (MSI), conteniendo el equivalente de 75 puertas lógicas y comúnmente empaquetado en un DIP de 24 pines. La ALU de 4 bits de ancho puede realizar todas las operaciones tradicionales de suma, resta, decrementar, con o sin acarreo, al igual que operaciones lógicas AND, NAND, OR, XOR y SHIFT. Están disponibles muchas variaciones de estas funciones básicas, para un total de 16 operaciones aritméticas y 16 operaciones lógicas en dos palabras de cuatro bits. Las funciones de multiplicación y división no son proporcionadas, pero pueden ser realizadas en pasos múltiples usando funciones de SHIFT y suma o resta. SHIFT no es una función explícita pero puede ser derivada de varias funciones disponibles, incluyendo (A+B) más A, A más AB.
El 74181 realiza estas operaciones en dos operandos de cuatro bits que generan un resultado de cuatro bits con un acarreo en 22 nanosegundos. El 74S181 realiza las mismas operaciones en 11 nanosegundos, mientras que el 74F181 realiza las operaciones en típicamente 7 nanosegundos.
Múltiples 'slices' pueden ser combinados para tamaños arbitrariamente grandes de palabras. Por ejemplo, seis 74S181s y cinco generadores de acarreo look ahead 74S182 pueden ser combinados para realizar las mismas operaciones en operandos 64 bits en 28 nanosegundos. Aunque fue eclipsado por el desempeño de los microprocesadores de 64 bits de multi gigahertz de hoy, esto fue absolutamente impresionante cuando comparaba a las velocidades de reloj de submegahertz de los tempranos microprocesadores de cuatro y ocho bits.
SEBASTIAN AARON ESCUDERO FERNANDEZ