Doubts with ctmm.fit, akde calculation and PMF/PDF
Elena Bravo
Christen Fleming
Elena Bravo
Christen Fleming
Elena Bravo
Christen Fleming
Elena Bravo
Christen Fleming
Elena Bravo
Christen Fleming
Jorge .Rodríguez Pérez
Hi Chris,
I would like to continue asking you about some doubts that are mentioned in this thread.
In my case, I also work with several individuals with large datasets, above 100 thousand data in several cases, somewhat irregular with duty cycling, so at first, I also saw it necessary to use the argument weight=TRUE. This led me to processing times that could exceed 72 hours per individual and even some individuals from whom I could not get any results.
After your last message, I found that my sampling is not as irregular and abrupt as you mention, with many cycles observed and effective sampling areas DOF [area] >10 (mean 220, range 23.8 – 841). All this led me to the idea of using weights=FALSE and check that processing times decrease drastically.
My doubt also arises in determining whether to use the weight argument or not. As you recommended, I have classified my individuals in ascending order of DOF [area] and calculated both models weights=TRUE and weights=FALSE to check the differences between them until I find the point in which they were minimal or non-existent. But so far, I can't find that point. Individuals with lower DOF [area] may have smaller differences than individuals with higher DOF [area] or vice versa without a clear pattern in which the differences decrease as DOF [area] increases. Even in one of the individuals analyzed, the core with the highest probability of presence moves completely not using this argument. The only trend that I have been able to verify, although it is not always fulfilled, is that using weights = TRUE drifts to larger presence areas.
At this point I start to be skeptical of whether to use the argument or not, because I'm afraid to not use it and be overestimating the area. However, applying weight=TRUE there are some individuals that I can not calculate due to processing times.
Do you think that using weight=FALSE could lead to these overestimates? And if there is no clear pattern that allows you to choose which individuals to use with and without weights = TRUE, is there any other approach to choose it?
I would also like to ask you about how to interpret the values of the PDF. I would like to make comparisons between the probability of presence of several individuals. As I have interpreted, PDF is the one I should be using. However, the results between different individuals may have differences of several orders of magnitude for the maximum value of presence probability. This leads me to wonder if normalize to 1 all the individuals is the right thing to do to be able to compare them. Could I use the CDF for this purpose as well?
Thank you very much in advance!
Jorge.RP
Christen Fleming
Jorge .Rodríguez Pérez
Hi Chris,
My tags are configured to collect information at 5-minute intervals, with winter periods in which the collection was limited to every 30 minutes in order to save battery and suppression of night records.
Progress do shows when trace=TRUE and I am using the most recent version available. With these slower individuals, what happens is that after a long time of processing, the progress of trace=TRUE stops appearing, as if the program were hanging, forcing me to restore session. It could even be a problem of the capacity of my computer, although in others that I have tested it does not seem to work either.
As far as I can tell, or interpret, neither do I have giant gaps in the data for the majority of birds. Yet, the example given in vignette ('akde') is what may be happening in the individual who changes the core with the highest probability of presence. Did not know about this fact, but looking at the sampling of this individual, it makes sense to me.
The only explanation I can think of is that these individuals I can not calculate seem to match those who make larger dispersive flights. I attach two images of two individuals calculated with weights=FALSE. Most of the locations are in the same area, while these individuals tend to make dispersive flights that can last several days (or even months) through areas that they never revisit. Most individuals with whom I cannot calculate the model with weights = TRUE perform this type of flight, in addition to being the ones with the highest numbers of data, and I do not know if that can affect the processing time and number of calculations.
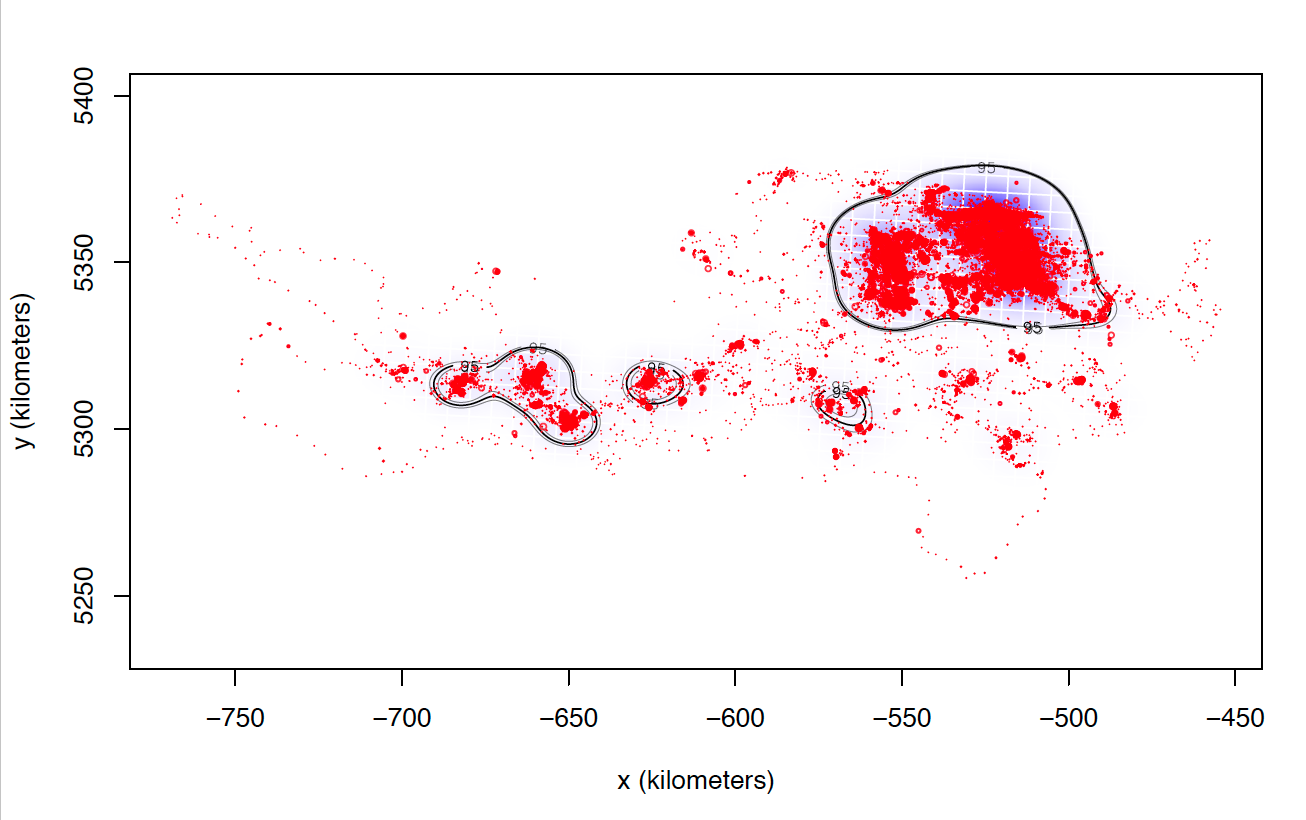
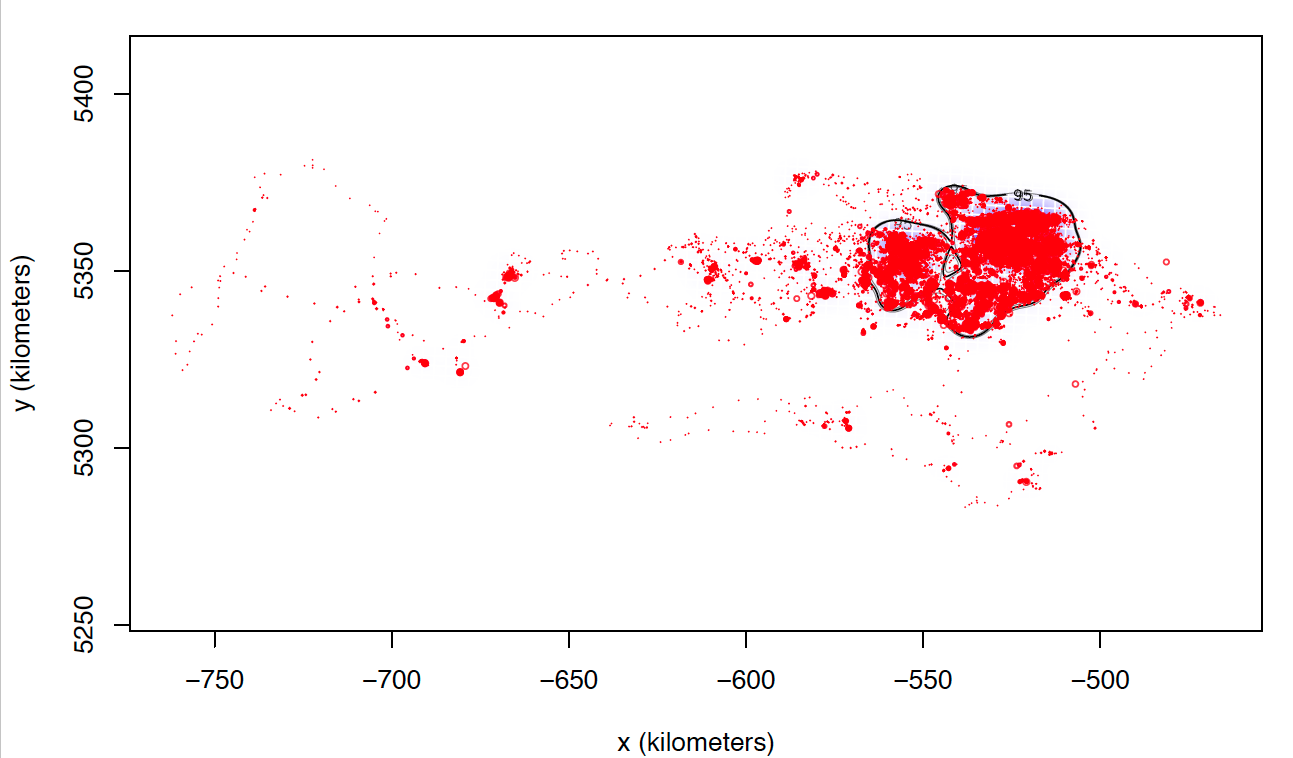
Anyway, I still have the doubt of the cases in which I have calculated both models weights = TRUE and weights = FALSE that present differences between them although not excessively large. So far, I have not found a justification that allows me to follow the same criteria to choose one or the other and that is met in all individuals.
Regarding the use I want to give to the PDF, my intention is to obtain a final raster with the probability of joint presence for all my individuals. I have tried to use the mean function and it seems that I get the results I was looking for. My doubt arises because the maximum value of presence can have differences of several orders of magnitude between individuals and I do not know if they are comparable to each other. For example, the pixel with the highest probability of presence found in the core of individual A's home-range may have the same value as a marginal zone pixel of individual B's home-range. For individual A, that is the area with the greatest probability of presence, but I do not know if it is comparable to the area of greatest presence of individual B. As my ultimate goal is to obtain a map with the use of the territory of the population as a whole, I do not know if it makes sense to first normalize the camping areas for each individual and then obtain the joint result in a GIS environment, or if the mean function serves my goal. I also have the doubt if instead of the PDF for this purpose, I can use the CDF as it already have the accumulated probability.
Thank you for the quick response!
Jorge.RP
Christen Fleming
Jorge .Rodríguez Pérez
Hi again Chris,
Thank you very much for the involvement.
I send you two datasets (individual 6529 and individual 5433) with which I have problems calculating the models with weights=TRUE. It seems to me, especially after your explanations, that these two individuals are problematic because of inconsistencies in sampling. You can see that for none of them the duty cycling corresponds exactly to the configuration that would correspond to it, since these are probably the two individuals with the worst dataset quality. For both cases, I interpret that weights=TRUE attribute as necessary. 5433 took me approximately 48 hours to obtain it, while for 6529 I had to stop the process after more than 72 hours, with trace=TRUE returning only a single record after that time.
I also give you an example of an individual (7228) with a much more consistent sampling, but also with some irregularities according as I can understand. For this case, weights=TRUE is not a problem, performing the process in about 5 hours. What surprises me is that being approx. twice as many records, there are those temporal differences.
For this last individual, weights=TRUE and weights=FALSE has different results, although relatively acceptable. For the current project I am doing, assuming weights=FALSE in most individuals seems reasonable to me considering the processing time, but I am not sure that this is the case either. Do you think those differences can be assumed, especially considering that it is for a master's thesis, with the future aim of using weights=TRUE for all cases?
Regarding the population map, yes, I had used the mean function and the result is what I wanted to achieve. But I still have the doubt of whether I wanted to compare two individuals with each other, the values of the PDF are still comparable even having the maximum values of probability several orders of magnitude of difference.
Again, thank you very much for the involvement and I hope to not be bothering you!
Here is the link to the datasets: https://drive.google.com/drive/folders/1Q7EVKHFYKFU7boc6Bb-tS8cvP7CyRvAV?usp=sharing
Jorge.RP
Christen Fleming
Jorge .Rodríguez Pérez
Hello again Chris,
Seriously, thank you very much for the involvement.
I could not confirm you if individual 6529 is the most problematic. I would even venture to say that individual 5433 has even more irregular sampling. I can't compare individual 6529 yet, but take a look at the differences between weights=TRUE and FALSE for individual 5433.
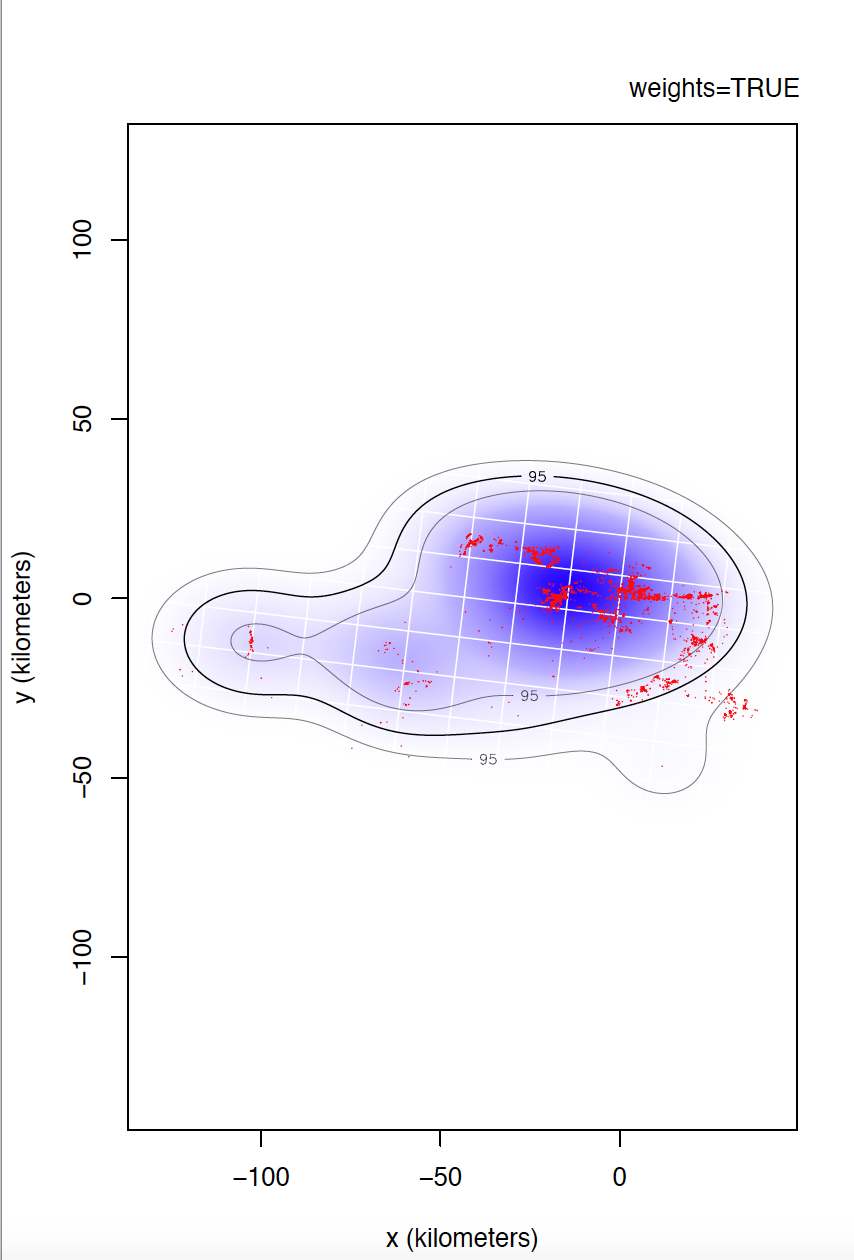
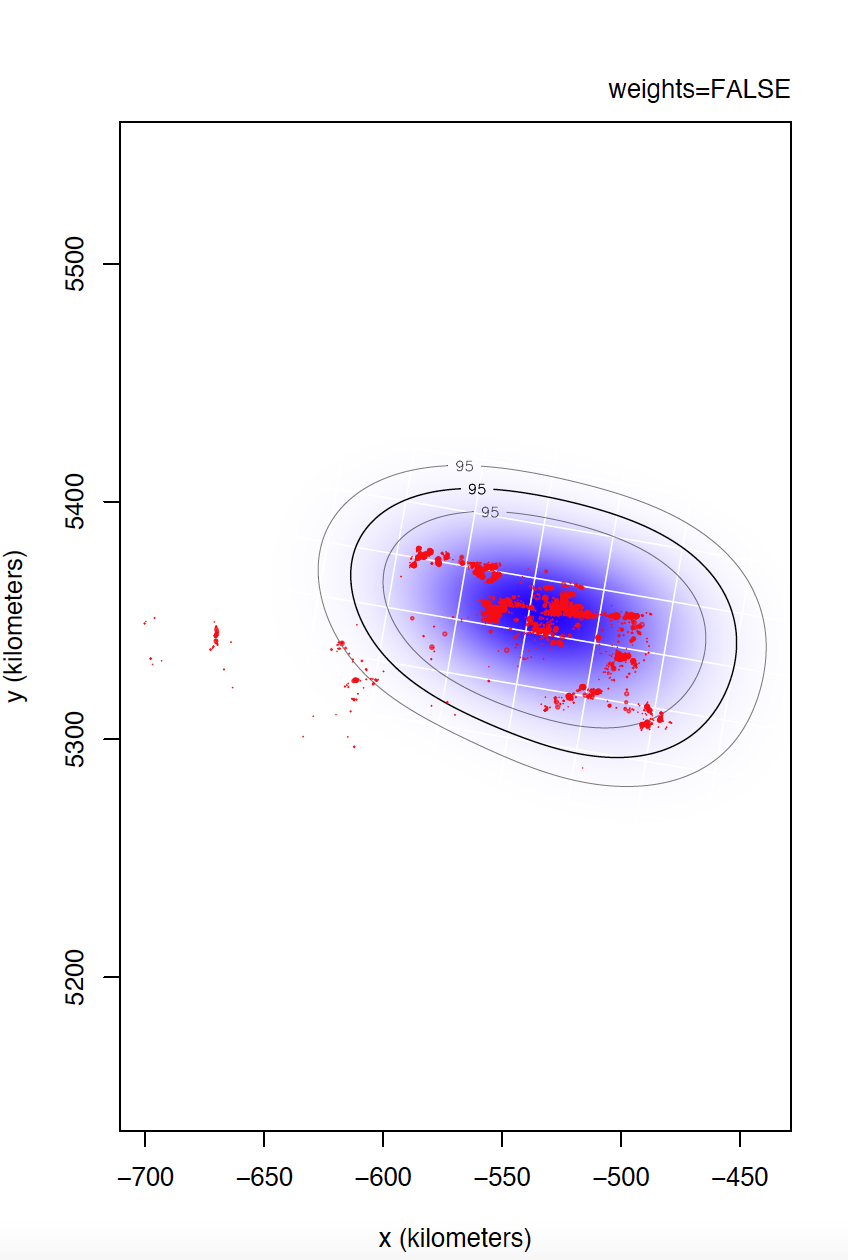
Yes, data is of e-obs variety, specifically first-generation tags. As you said, e-obs horizontal accuracy estimateis is "missing". According to the paper you are quoting, as.telemetry imports the values of e-obs horizontal accuracy estimate as HDOP values, so I renamed this variable like this, is not that horizontal accuracy estimate is missing. I should have tell about this. Could this have caused more problems than benefits? Anyway, I upload to the same link the datasets directly extracted from movebank without any filter if that can help.
Regarding the last part, sorry for being a pain. On the one hand, I want to compare the probability of presence for the entire population with other risks maps. Mean function is what I am using to obtain distribution raster maps, and works fine for what I want. On the other hand, I also want to compare the risks presented by each individual. This is where I wonder if the maximum probability values of presence are comparable to each other even with values of different order of magnitude. If the values for individual A at the core of its range are the same as the values for individual B in a marginal zone of its distribution, does it mean that these values are comparable and so, that the maximum probability of presence for A in its core area is less than the maximum probability that B would have in its core? Could the data be first normalize in order to make it comparable to each other and that the values of the core area of A are equal to the values of the core area of B?. All this assuming I use the PDF. That is why at first, I thought about using the CDF.
Thank you so much
Jorge.
Christen Fleming
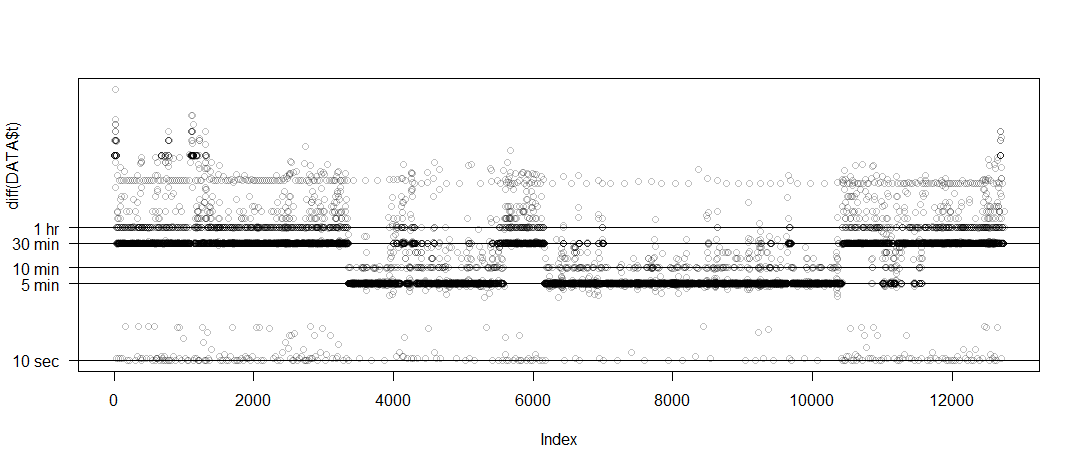
Elena Bravo
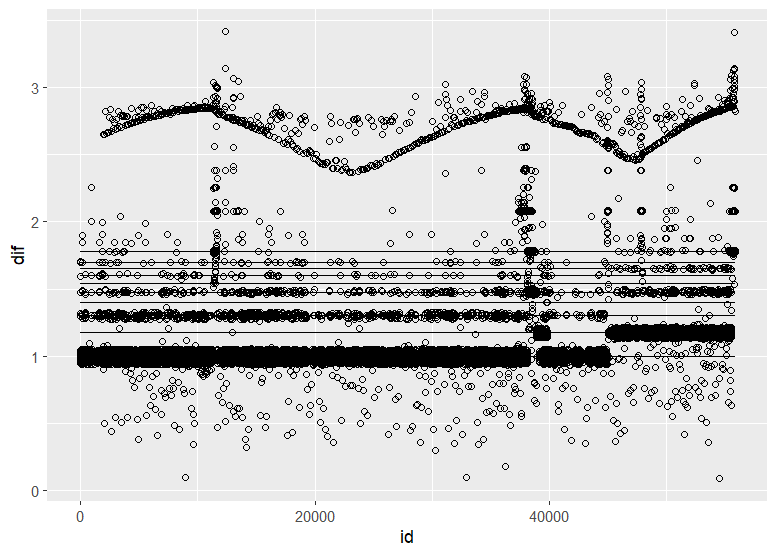
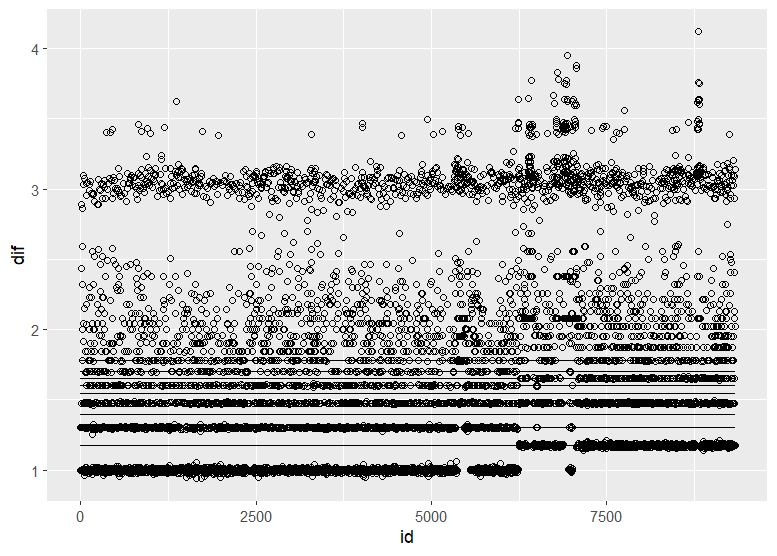
Christen Fleming
Ben Carlson
--
You received this message because you are subscribed to the Google Groups "ctmm R user group" group.
To unsubscribe from this group and stop receiving emails from it, send an email to ctmm-user+...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/ctmm-user/1d87f272-f73a-4261-8829-04a838805518n%40googlegroups.com.
Christen Fleming
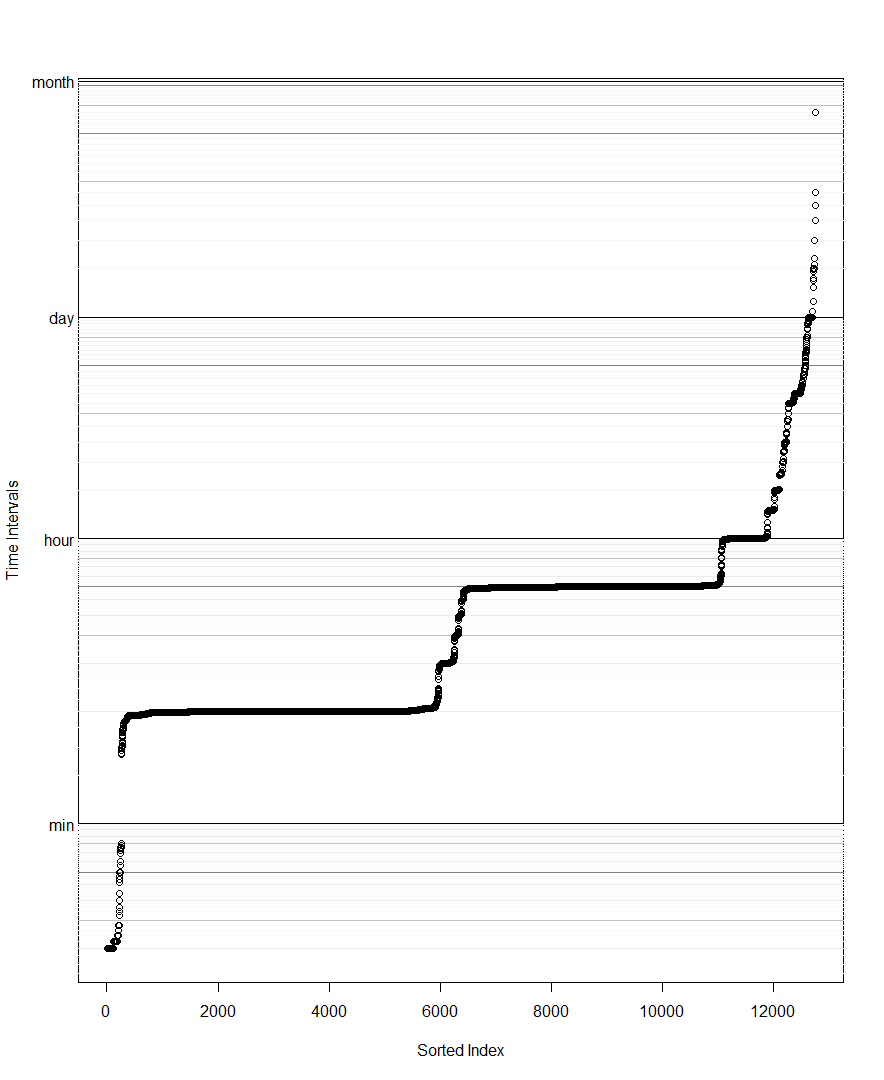
DT <- DT[DT>0] # remove for log scale
DT <- sort(DT) # Beth's idea
plot(DT,log='y',yaxt='n',ylab='diff(time)',col=rgb(0,0,0,1/4))
# example horizontal line with labeled tick
abline(h=1 %#% 'hr')
axis(side=2,at=1 %#% 'hr',label='1 hr',las=2)
Francisco Castellanos
To view this discussion on the web visit https://groups.google.com/d/msgid/ctmm-user/cf38be5e-a423-4db6-9972-b320655b7f41n%40googlegroups.com.
Christen Fleming