BBB(5, 2) > 10^502

[Shawn Ligocki]

I'm excited to share with you all some exciting new BBB(5, 2) results. Please see my blog post for the details: https://www.sligocki.com/2022/02/17/bbb-5-2-search-results.html

The headliner is that I have a new champion demonstrating that BBB(5, 2) > 10^502!

The machine is:

1RB 1LC 1RC 0RD 0LB 0RC 0RE 1RD 1LE 1LA

       +-----+-----+

       |  0  |  1  |

   +---+-----+-----+

   | A | 1RB | 1LC |

   +---+-----+-----+

   | B | 1RC | 0RD |

   +---+-----+-----+

   | C | 0LB | 0RC |

   +---+-----+-----+

   | D | 0RE | 1RD |

   +---+-----+-----+

   | E | 1LE | 1LA |

   +---+-----+-----+

which I calculate as quasihalting on step:

17343555453073487632568831998524647611476122721387575109809110508040305881313770086405857253466944032587116455285023340679026743153434568269090999646673982279082956158857498176561296890271859824899413371164121236773083504487750883780345179786701667361350140269491468865274445926123208946988441936073654439706644906799980448112435008230447458411447341953802864752401263139355549814447277254297064076934216788633169444656946152362269030511952540133190262122812094646680539368211780404865521194338123470785

(>1.7 * 10^502)

Cheers,

-Shawn

[nichol...@gmail.com]

Holy smokes, what a find! And your repo is converted to Python 3! Lots of presents under the "Christmas tree" today!

I've attached a picture of the new champion program's control flow graph. It isn't very complicated, and the whole program can be rewritten to be fully structured, without any goto statements at all.

This is further evidence that the Spaghetti Code Conjecture is FALSE. These champion programs implement exotic Collatz-like functions, but the implementations are straightforward. The complexity comes from the math itself and not from any code tricks.

On the other hand, all the champion programs that have been found are necessarily amenable to analysis. The Ligocki simulator doesn't just run programs really fast; it uses forward reasoning to apply high-level iterations in one fell swoop. So it's no surprise that the programs turned up are relatively simple -- if they weren't simple, they wouldn't be amenable to analysis, and they wouldn't have turned up in the first place!

Taking this skeptical position to the extreme, we end up in a situation where all available evidence points to the SCC being false, while all evidence in favor of it is necessarily unobtainable.

Actually, this same argument can be carried over to suggest that the classic Collatz conjecture might be false. A counterexample would necessarily be a massive number, perhaps so large that it couldn't be specified in Peano arithmetic. Thus any attempts to verify the conjecture up to some bound are not worth much, since any bound that can be reached is, relative to a possible counterexample, quite puny.

[Shawn Ligocki]

And here is the promised analysis: https://www.sligocki.com/2022/02/22/collatz-complex.html

The tidiest Collatz-like function I have found is:

g(x, n, m) = 0^inf bin(x) 1^n <E 1^m 0^inf

• g(2x+1, n, m) = g(x, n+1, m)
• g(2x, 3k + 1, m) -> g(4x+2, 5k + m, 2)
• g(4x, 3k + 2, m) -> g(8x + 2, 5k + m + 1, 2)
• g(4x + 2, 3k + 2, m) -> g(8x + 2, 5k + m + 1, 2)
• g(0, 3k, m) -> Quasihalt
• g(2x, 3k, m) -> g(x, 0, 5k + m + 1)

Which iterates 2262(!) times starting at step 8 (g(0, 1, 3)) before Quasihalting. But I have a little more exploration of the intuition behind this in the article. If anyone else has a tidier analysis or more intuition about the behavior of this machine, I am very interested to hear it!

-Shawn

--
You received this message because you are subscribed to the Google Groups "Busy Beaver Discuss" group.
To unsubscribe from this group and stop receiving emails from it, send an email to busy-beaver-dis...@googlegroups.com.
To view this discussion on the web visit https://groups.google.com/d/msgid/busy-beaver-discuss/d231f4a3-6c3a-4826-8e0f-4ebfc84ac4een%40googlegroups.com.
For more options, visit https://groups.google.com/d/optout.

[Shawn Ligocki]

Thanks for the flow diagram, Nick. Could you share an example of how this machine looks written in a "fully structured" way (w/o goto statements) as you mentioned? Do you think that there is a way to formalize this sort of statement so that we can mathematically define some TMs as structured and others as un-structured? Or is it more of a intuitional aid or game where you try to rewrite a simulator incrementally from a goto heavy one to a structured program?

On Fri, Feb 18, 2022 at 12:19 PM nichol...@gmail.com <nichol...@gmail.com> wrote:

--

[Nicholas Drozd]

The current 5x2 BBB champion program is:

- 1RB 1LC 1RC 0RD 0LB 0RC 0RE 1RD 1LE 1LA

This can be transliterated into C:

/**************************************/

int main(void)
{
A:
if (BLANK)
{
// A0
PRINT;
RIGHT;
goto B;
}
else
{
// A1
LEFT;
goto C;
}

B:
if (BLANK)
{
// B0
PRINT;
RIGHT;
goto C;
}
else
{
// B1
ERASE;
RIGHT;
goto D;
}

C:
if (BLANK)
{
// C0
LEFT;
goto B;
}
else
{
// C1
ERASE;
RIGHT;
goto C;
}

D:
if (BLANK)
{
// D0
RIGHT;
goto E;
}
else
{
// D1
RIGHT;
goto D;
}

E:
if (BLANK)
{
// E0
PRINT;
LEFT;
goto E;
}
else
{
// E1
LEFT;
goto A;
}
}

/**************************************/

This C code has exactly the same control flow as the TM program.
Unlike the primitive TM assembly language, we can go a step further
and rewrite this into structured code. I claim that the following is
equivalent:

/**************************************/

int main(void)
{
while (1) {
if (BLANK)
{
// A0
PRINT;
RIGHT;
}
else
{
// A1
LEFT;

while (!BLANK) {
// C1
ERASE;
RIGHT;
}

// C0
LEFT;
}

while (BLANK) {
// B0
PRINT;
RIGHT;

while (!BLANK) {
// C1
ERASE;
RIGHT;
}

// C0
LEFT;
}

// B1
ERASE;
RIGHT;

while (!BLANK) {
// D1
RIGHT;
}

// D0
RIGHT;

while (BLANK) {
// E0
PRINT;
LEFT;
}

// E1
LEFT;
}
}

/**************************************/

This version is fully structured. It has no GOTO statements, and it
doesn't even have any BREAK or CONTINUE statements (which are really
GOTOs in disguise). There is only one true branch, and that's where
state A decides whether to go to C and then B or just straight to B.
(Notice that state C doesn't really exist in the new version; it has
been inlined directly into A and B.)

The loops that check for marks are guaranteed to terminate, the loops
that check for blanks can run forever. Indeed, it's at the E0 loop
that the program actually ends up quasihalting.

In this case, rewriting into structured form is straightforward. Are
there any cases where this cannot be done at all? That is, are there
programs that cannot be rewritten without using BREAK or CONTINUE? I
don't know how to prove that, but I think so. Consider the wild
program discovered by Boyd:

- 1RB 0RC 1LB 1LD 0RA 0LD 1LA 1RC

I've taken a crack at that one a few times and the best I've come up
with is a version with three CONTINUE statements. There's still just
one main loop, but it terminates and restarts under several
conditions. It's very complex, and the behavior is not easy to
describe. My feeling is that that is true spaghetti code.

Tools for structuring TMs:

- Convert TM to C
- https://github.com/nickdrozd/busy-beaver-stuff/blob/main/c_prog.py

- C code to run the structured version, along with examples
- https://github.com/nickdrozd/busy-beaver-stuff/tree/main/machines/structured

- Convert TM to control flow graph
- https://github.com/nickdrozd/busy-beaver-stuff/blob/main/dump_graphs.py

(I haven't actually tested the rewritten version above because it runs
too long, but I'm pretty sure it's correct. Also I hope the code
formatting comes out alright.)

[Shawn Ligocki]

Thanks Nick. This does seem a bit difficult to define rigorously. For example, it is easy to write any TM without goto's if you store the state in a variable. Ex:

char state = 'A';

while (state != 'Z') {

  if (state == 'A') {

    if (BLANK) {

      // A0 -> 1RB

      PRINT;

      RIGHT;

      state = 'B';

    } else {

      // A1 -> 1LC

      LEFT;

      state = 'C';

    }

   } else if (state == 'B') {

     if (BLANK) {

       // B1 -> 1RC

       RIGHT;

       state = 'C';

     }

  ...

}

But certainly this is not a very structured program so we have sort of failed at the spirit of the challenge. I guess in your code you actually have no variables, you are restricting yourself to opaque commands (BLANK, PRINT, ERASE, LEFT, RIGHT) and standard control flow (if, while, ... goto) and also no functions/subroutines. But you are allowing limited duplication (where you've inlined code for state C twice).

Interesting, I will have to think on this :)

[Shawn Ligocki]

OK, I have a theory on how to formalize mathematically the concept of a "structured TM" or at least a goto-less TM. Nick, inspired by one of your posts, I decided to think about this purely by analyzing the state flow diagram for the machines (ignoring the read/write/dir information). Here is my procedure:

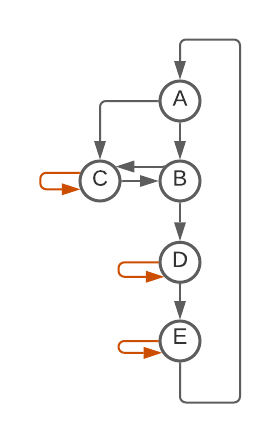
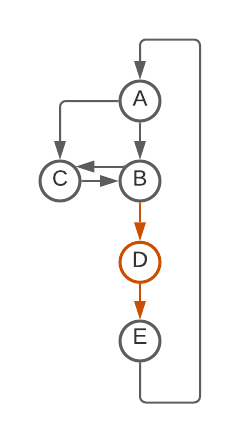
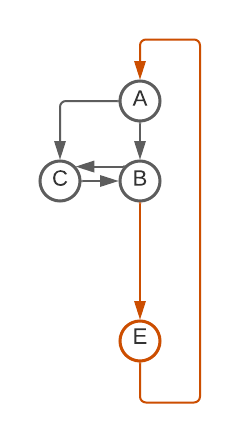
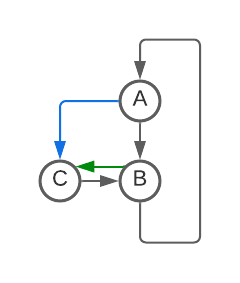
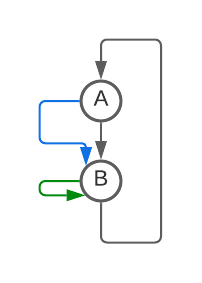
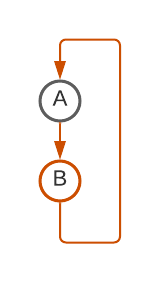
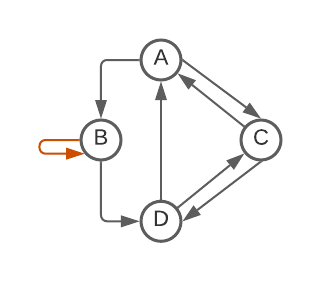
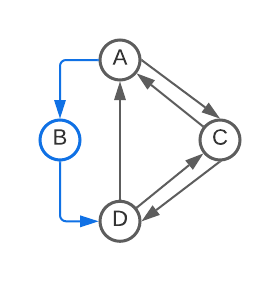
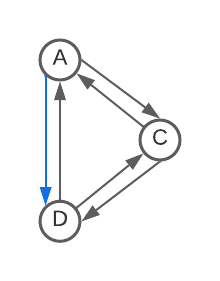
1. Delete all self-loops [This seems to correspond to using while loops for all transitions that stay in the same state].
2. De-duplicate duplicate arrows between states (If there were two edges A->B, delete one) [This seems to correspond to using an if statement, you can do a different action depending on read symbol, but at the end control flow continues to the same destination regardless].
3. This one is slightly more complicated: For any state with only one arrow leaving it (Say D->E in the second diagram below): remove that node and update all incoming arrows to point to that single next state (E). [This seems to correspond to inlining and can lead to a finite increase in code duplication].

Repeat until nothing changes.

If you apply this to my BBB(5, 2) champ, it repeatedly removes states until none are left. [I'm interpreting each arrow as a goto, so this is equivalent (I think) to saying that this machine can be written with no gotos]. Here is visual progression of this algorithm (First removing all self-loops; then collapsing nodes using Rule 3: D, E, then C; remove duplicate edge and self-loop; collapse node B using Rule 3):

If you apply it to the Boyd machine you listed, it removes state B (which can be inlined to come between A and D), but that's it, then it's stuck with a fully connected digraph with 3 nodes A, C, D (all pointing to both of the others). [I'm interpreting this to mean that we cannot refactor this machine to be goto-less ... with some not 100% constraints on what we're allowed to do :) ]. Here is a visual progression of this algorithm:

I coded this up and ran it on the full of machines I have for various domains and the results are:

• 2x2 - 100% structured (Actually, all 2 state machines are completely structured because all of their arrows are either self-loops or going to the only 1 other state node)
• 3x2 - 95% structured
• 4x2 - 86% structured
• 5x2 - 71% structured (I only did a random sample of these, but it seems to be accurate to this precision)

Of note: This is a % of the Tree Normal Form enumerated machines (not all possible TMs. If you looked at the % over all possible TMs these numbers would probably change drastically).

So this is pretty high. Most TMs I'm simulating are structured (so, in that sense, it's not too surprising that the champion is structured). Then again, the fraction of unstructured TMs is increasing rapidly, so perhaps it could be useful to direct our search in larger spaces.

Furthermore, in the 5x2 case, we expect ~3/10 TMs to be unstructured, but if I look at the top 20 BBB(5, 2) candidates, they are all structured, so perhaps that is of note! Then again perhaps it is simply an indication of the blindness of our simulator. I'm guessing that unstructured TMs are harder to accelerate the simulation of. As Nick and I have mentioned before, there's a significant bias in the results we get based upon the machines we can interpret at a sufficiently high level.

Either way, I'm excited by the prospect of being able to add a new explicit prediction to the Spaghetti Code conjecture:

Are all Busy Beavers (or Beeping Busy Beavers, etc) structured TMs?

or maybe:

Are all but a finite number of Busy Beavers unstructured TMs?

What do you all think? If I had to guess: I am inclined to predict the second one: that Busy Beavers we've found so far being structured is merely and artifact of the fact that we're only looking at small machines with tools that naturally encourage finding orderly results. But, as Nick says, that is a weird position to be in, where all the available evidence suggests that all BBs are structured, but evidence to the contrary is harder and harder to produce.

Is it possible to avoid these sorts of bias? I suppose one idea would be to do a survey of the TM landscape without an accelerated simulator that takes advantage of structure. If such a direct simulator found that the halting times for structured vs unstructured TMs were comparable or not comparable, then maybe that could give some indication. Say if using a direct simulator, the histogram of halting times for structured vs unstructured TMs were statistically indistinguishable (in some way), could we predict that among top BBB machines 29% should be unstructured? Of course that is assuming that normal TM behavior is extrapolatable to exceptional TMs (Busy Beavers), which is probably a pretty foolish extrapolation ... but still it would be interesting to see what's going on here!

-Shawn

PS For anyone who wants to test if TMs are "structured" or not, you can run:

$ python3 Code/Flow_Diagram_Collapse.py TM_FILE -n LINE_NUM

to get the results for a single TM or:

$ python3 Code/Flow_Diagram_Collapse.py TM_FILE

to summarize the % of TMs in a file which are structured (one TM / file)

You will need to:

$ python3 -m pip install networkit

[Nicholas Drozd]

Your graph reduction procedure definitely captures the process I've been going through in manually structuring these things, and it's a great way to formalize the Spaghetti Code Conjecture.

I still think the SCC is false. Even if we accept the skeptical argument that the available evidence doesn't mean much, the lesson of Scott's Bigger Number Game is that theory beats tricks. What we should expect if we believe Scott's thesis is that champions will ignore tricks and exploit theory. And that indeed is what they do.

Questions:

  1. Has this sort of graph reduction been studied before?

  2. "Repeat until nothing changes." Is there an upper bound for how long this will take? It's computable, so the procedure definitely will terminate, but when?

I ran the procedure against my own set of test cases, and most of them came back simple. One notable exception is the 5x2 program discovered by Uwe Schult in 1982. It halts after 134,467 steps, and it reigned as champion for two and a half years.

  --> 1RB 0LC  1RC 1RD  1LA 0RB  0RE 1R_  1LC 1RA

The control flow diagram is attached.

[Shawn Ligocki]

On Wed, Feb 23, 2022 at 4:32 PM Nicholas Drozd <nichol...@gmail.com> wrote:

Your graph reduction procedure definitely captures the process I've been going through in manually structuring these things, and it's a great way to formalize the Spaghetti Code Conjecture.

Woohoo! 

I still think the SCC is false. Even if we accept the skeptical argument that the available evidence doesn't mean much, the lesson of Scott's Bigger Number Game is that theory beats tricks. What we should expect if we believe Scott's thesis is that champions will ignore tricks and exploit theory. And that indeed is what they do.

I am slightly skeptical of this reasoning: The Big Number game is a human endeavor, so theory is easier for us to reason about and use. BB is a space of arbitrary rules that sometimes are have massive success at making big numbers, but they need not "prove" that they produce big numbers, they don't even "know" that they have been so successful, it is just "chance" (at least in my mind :) ). But either way, I do agree that it is exciting to see theory beat tricks so far :)

Questions:

  1. Has this sort of graph reduction been studied before?

I would also love an answer to this question :) Perhaps I will try writing it up in my blog and maybe ask on CS Overflow or something like that ... 

  2. "Repeat until nothing changes." Is there an upper bound for how long this will take? It's computable, so the procedure definitely will terminate, but when?

Each modification reduces the number of edges (remove self-edge; remove duplicate edge; or in the 3rd case, it removes the one out-edge and updates all the in-edges to point to a new target), so it is bounded by the number of edges, which is the same as the number of transitions.

But there is a related question I'm not 100% sure about: Could you reach a different result depending on which order you remove things? Say which order you collapse nodes using rule 3? I have a hunch that it doesn't matter, but certainly no proof :/

 

 

I ran the procedure against my own set of test cases, and most of them came back simple. One notable exception is the 5x2 program discovered by Uwe Schult in 1982. It halts after 134,467 steps, and it reigned as champion for two and a half years.

  --> 1RB 0LC  1RC 1RD  1LA 0RB  0RE 1R_  1LC 1RA

The control flow diagram is attached.

Thanks for sharing!

3/20 top 3x3 BBB champs are also "Unstructured" (although I'm considering renaming this to "Sequential" vs. "Non-sequential" since I think these machines can clearly still have some structure). Here's the longest running:

1RB 2LC 2RA  1LA 2LB 1RC  1RA 2LC 1RB

which runs 2513054429677251202664472 (>2.5 * 10^24) steps before quisihalting.

I also did a more broad survey and of all the 5x2 BB enumerated machines (so all must have a halt-transition or at least one undefined transition):

• Of proven halting TMs: 29_739_386 / 34_358_413 = 87% are structured
• Of proven infinite TMs: 78_917_855 / 92_525_161 = 85% are structured
• Of uncategorized / holdout TMs: 7_448 / 8_031 = 93% are structured

The distinction between halting and infinite is surprisingly minimal (suggesting that there is not actually a correlation between structure and "normal" halting-ness). But the holdouts are notably more structured than everything else! Which surprised me because I'd have thought we'd have an easier time simulating (and thus proving) structured programs ... mysteries abound!

-Shawn

[Nicholas Drozd]

The graph reduction procedure you've described is to do the following
until no changes are made:

0. Purge nodes with no arrows.
1. Delete duplicate arrows.
2. Delete reflexive arrows.
3. Inline any node with just one exit point.

There is one more step that can be added:

4. Inline any node with just one entry point.

This catches cases like `1RB 0LC 0LC 1RA 0RA 1LD 1LA 1LC`: D is
only reached from C, so we may as well just say that the D code
belongs to the 1-branch of C.

The ultimate issue I think is that branches are hard to understand.
When we delete a reflexive arrow, it's because that arrow represents a
while-loop, after which comes the remaining arrow. That's not a true
branch; it's just a sequence that happens to be implemented with a
branch. But some branches are true branches, and those are not easy to
figure out.

You mentioned that all 2-state programs are simple according to this
reduction procedure. That is true irrespective of the number of colors
involved! We might say that the SCC is trivially true for 2-state
K-color programs (K > 3) because all such programs are totally opaque
to control flow analysis. They do all their work with branching, and
branching is too difficult.

Let me make one further argument against the SCC. Most programs are
structured, or at least relatively structured compared to how bad they
could be (see next paragraph). True spaghetti is rare. If the SCC were
true, then we could just focus searching on just the space of
spaghetti programs, which is significantly smaller than the space of
all programs. That certainly would make searching much easier! But it
also seems TOO GOOD TO BE TRUE. Graph analysis belongs to the world of
computability, and therefore it has to fail.

Here's one more thing to consider. Suppose we run a program through
the graph reduction procedure and it isn't completely simplified away.
Call this the kernel of the program. How many nodes are there in the
kernel compared to the number of states in the program? In the case of
Boyd's program, we start with four nodes and end up with three, so one
node was simplified away.

If we take an 8-state program and reduce it to a 3-node kernel, we
might say that there's a little spaghetti in there, but not much, and
so it's mostly structured. A strong form of the SCC would say that no
reduction at all should be possible, or maybe just a little bit.
Notice that for maybe-halting 2-color programs, one state can always
be reduced, namely the state with the halt instruction.

[Shawn Ligocki]

On Thu, Feb 24, 2022 at 1:18 PM Nicholas Drozd <nichol...@gmail.com> wrote:

There is one more step that can be added:

  4. Inline any node with just one entry point.

This catches cases like `1RB 0LC  0LC 1RA  0RA 1LD  1LA 1LC`: D is
only reached from C, so we may as well just say that the D code
belongs to the 1-branch of C.

Hm, I'm not sure about this step 4. I think it works fine as a final step (you can remove one goto by inlining nested if statements), but afterwards, I feel like you might not be able to apply the other rules anymore, ex, let's say I applied rule 4 to the code version of this. I would end up with something like:

C:

  if BLANK:

    # C0 -> 0RA

    ERASE; RIGHT;

    goto A

  else:

    # C1 -> 1LD

    PRINT; LEFT;

    if BLANK:

      # D0 -> 1LA

      PRINT; LEFT;

      goto A

    else:

      # D1 -> 1LC

      PRINT; LEFT;

      goto C

and in the Flow diagram I'd have a self-loop C->C and two arrows C->A. I guess we can remove the duplicate C->A arrow by moving the goto A's to the end, like:

C:

  if BLANK:

    # C0 -> 0RA

    ERASE; RIGHT;

  else:

    # C1 -> 1LD

    PRINT; LEFT;

    if BLANK:

      # D0 -> 1LA

      PRINT; LEFT;

    else:

      # D1 -> 1LC

      PRINT; LEFT;

      goto C

  goto A

but I'm not convinced this generalizes to more complex examples. And worse, I don't see any way to remove the self-loop C->C because we are no longer converting a single if-else clause into a loop, now we have nested if-statements.

[Nicholas Drozd]

Starting from your first C block, first remove the elses. They aren't needed because if the blank check succeeds, a jump will get executed.

    C:
      if BLANK:
        # C0 -> 0RA
        ERASE; RIGHT;
        goto A

      # C1 -> 1LD
      PRINT; LEFT;

      if BLANK:
        # D0 -> 1LA
        PRINT; LEFT;
        goto A

      # D1 -> 1LC
      PRINT; LEFT;
      goto C

Now it's a block that ends with an unconditional jump to the beginning of the block. Well, that's just a while-loop.

    while (1) {

      if BLANK:
        # C0 -> 0RA
        ERASE; RIGHT;
        goto A

      # C1 -> 1LD
      PRINT; LEFT;

      if BLANK:
        # D0 -> 1LA
        PRINT; LEFT;
        goto A

      # D1 -> 1LC
      PRINT; LEFT;
    }

This block now has just one exit point (A), and it can be inlined at any C callsite, thereby eliminating both C and D.

I can't prove that adding step 4 doesn't ruin the procedure! But the machines of Boyd and Uwe still can't be reduced even with step 4, which suggests that the step isn't too powerful. And everything else I've checked it against that can be reduced without step 4 can still be reduced with it.

And we don't have to decide on any of this once and for all. We could mix and match different elimination steps and consider the resulting graphs. A procedure that eliminates all graphs wouldn't be very interesting, but anything short of that might be worth looking at.

[Shawn Ligocki]

I wrote up a blog post about how the BBB search is conducted: https://www.sligocki.com/2022/02/27/bbb-search-process.html

It focuses mostly on the types of recurrence that we can currently detect (Chain Recurrence, Lin Recurrence and PA-CTL Recurrence) with the hope of being a jumping off point for trying new techniques :)

[Nicholas Drozd]

Nice! Keep the posts coming!

An important point that stuck out to me:

> All Lin Recurrent programs are PA-CTR Recurrent.

Does this apply to all Christmas trees too? It would be nice if it
did, because then we could dispense with the elaborate classifications
of Xmas, Leaning Xmas, Double Leaning Xmas, etc.

Also the Chain Recurrence section mentions BBB(2, 4), but the program
displayed is BBB(4, 2).

[Shawn Ligocki]

On Mon, Feb 28, 2022 at 9:45 AM Nicholas Drozd <nichol...@gmail.com> wrote:

Nice! Keep the posts coming!

Great to hear! It's good to know someone's reading this stuff :) Keep the questions and feedback coming!

An important point that stuck out to me:

> All Lin Recurrent programs are PA-CTR Recurrent.

Does this apply to all Christmas trees too? It would be nice if it
did, because then we could dispense with the elaborate classifications
of Xmas, Leaning Xmas, Double Leaning Xmas, etc.

Short answer: Yes ... mostly ... I think.

In general, we do not have any Xmas tree specific code in our repo. This is overall because the Proof System (built mainly off of detecting PA-CTRs) is strong enough to capture the behavior of most Xmas trees ... that said, it can be finicky and sometimes I'll look at a machine that we failed to prove as infinite and it just looks like some sort of Xmas Tree variant and after digging in, I find that it does some sort of slightly weird behavior somewhere that tricks our detection. But, in general, PA-CTRs have been so strong that we don't feel any need to implement anything Xmas tree specific (which is great!) and mostly work on improving the PA-CTR system to cover more corner cases.

Unlike Chain Recurrence (trivial) and Lin Recurrence (fiddly, but reasonable), I don't think anyone has described an algorithm which will find all PA-CTRs rules ... in fact, I don't think we really even have a completely rigorous delineation of what count as PA-CTRs rules (is it any rule in which all exponents only change by a constant value each application? Does it have to be based on a fixed number of simulator loops? ...). Instead, in our code we have some heuristics that cause us to try and prove a PA-CTR rule. So, it happens that there are some machines which could theoretically be described by some sort of PA-CTR rule, but our system does not detect it.

But in the end, I feel like we have sort of two classes of machine now, looking through the eyes of tape compression:

• Machines whose tape compresses well. These machines use a lot of chain steps and thus build up big blocks of repeated symbols (or sometimes repeated blocks of symbols). Lin Recurrent TMs and Xmas trees both fit into this group. PA-CTRs tend to be quite successful on this class, and we spend time trying to improve it in this case.
• Machines whose tapes do not compress well (using our simple run-length compression). This includes counters and "chaotic" machines. PA-CTRs completely fail on these sorts of machines and we generally have to rely on other methods (CTL, Backwards reasoning, etc.) to try and classify them.

 

Also the Chain Recurrence section mentions BBB(2, 4), but the program
displayed is BBB(4, 2).

Yikes! Obviously a mistake because then below I show a tape with 2s on it! Fixed. Thanks! 

[nichol...@gmail.com]

I found another high-scoring non-champion 5x2 quasihalter:

  --> 1RB 0LC  0LD 0LB  1RA 1LA  1RE 1LD  1RE 1RA

It quasihalts after 10^315 steps. Not quite 10^502, but still 3rd place in Shawn's 5x2-Beep-Top list.