Sidewall drop data

[Allan in Portland]

Greetings,

List member Philip Williamson and I are putting together a Tire Pressure App that will compute the optimal air pressure for your tires based on the weight of you, your bike, your gear, and the frame geometry.

For those interested in gory details, I computed the slope and intercept for each tire width in BQ's published chart. Since the slope was clearly the biggest factor (they pretty closely converged with the same intercept at about 16lbs of load and 10PSI), I plotted the slopes from the widths we had, did a linear interpolation for widths between the measured points, and eye-balled a logarithmic curve for extrapolating to tires wider than 37mm. While I'm pretty happy with the pressure numbers we're getting, I'd be even more happy if I had some measured data points in the 42-55 mm range.

So, has anyone made their own sidewall drop measurements for wider tires?

BTW, we're pretty juiced about this app. We've been working on it evenings and weekends for a couple months and it's almost done. We hope to get it pushed out to all the usual Android marketplaces next week. I had planned to wait mentioning it on the list until after it was actually available, but now that we are so close, I decided to slightly ruin the surprise in the interest of more rigorous pressure computations. Also, if this goes well we're intending to do an iOS version (definitely) and then follow-up with a Sheldon-esque gear calculator app.

Thanks much,

-Allan

[Joe V]

I don't have any data but if you can't find any for wider tires, I should be able to give you optimal extrapolation values if you post the intercept/slope values for the data you do have. (I get paid for statistical work; I ride for free.) 

Joe 

[Allan in Portland]

Cool. I curious how they'll come out.

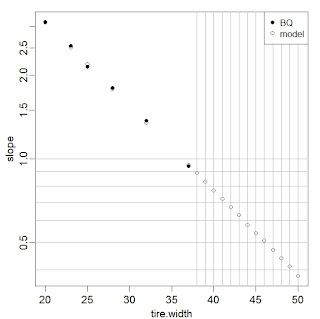
tire width (mm)		slope (PSI/kg)
20		3.1
23		2.55
25		2.14
28		1.8
32		1.37
37		0.94
43		0.85
50		0.8

43 & 50 mm are my estimates, the rest are measured from the chart printed in BQ.

Thanks,

-Allan

[Joe V]

Hi, Allan,

Here is what I found:

1. The data very strongly show that log(slope) is linearly related to tire width (technical details leading to this conclusion not shown...)

Here is  the regression  summary, where I used log = ln, that is, the natural log

            Estimate Std. Error t value Pr(>|t|)    

(Intercept)  2.52687    0.03621   69.78 2.53e-07

tire.width  -0.06965    0.00129  -54.01 7.04e-07

---

Residual standard error: 0.01794 on 4 degrees of freedom <-- this means the unexplained var'n has about a s.e. of 2% (which could partly be due to variation from reading the numbers off the table?).

Multiple R-squared: 0.9986,     Adjusted R-squared: 0.9983 

2. The results I get are as follows, where "slope" is the slope prediction (that is, i used the formula from the above to get log(slope) estimates, and then I exponentiated them.

   tire.width slope slope.BQ

1          20  3.11     3.10

2          23  2.52     2.55

3          25  2.19     2.14

4          28  1.78     1.80

5          32  1.35     1.37

6          37  0.95     0.94

7          38  0.89       NA

8          39  0.83       NA

9          40  0.77       NA

10         41  0.72       NA

11         42  0.67       NA

12         43  0.63       NA

13         44  0.58       NA

14         45  0.54       NA

15         46  0.51       NA

16         47  0.47       NA

17         48  0.44       NA

18         49  0.41       NA

19         50  0.38       NA

As you can see, my estimates for 43 and 50 mm are quite a bit lower than yours. 

Here are two graphs of the results. The first is linear in slope, the second is logarithmic (so a straight-line fit), with horizontal lines at each 0.1 units and vertical lines at each 1 unit in the region of interest.

I'll be interested to see if anyone will make some direct measurements!

Joe

[Wayne]

An poster on rec.bicycles.tech did extensive careful measurements of
tire drop data. I don't have time to search and find the link however
I saved a copy of it on my PC at the time and have copied the thread
below. Formatting makes it difficult but still possible to read.

Wayne



some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
1 of 13 12/23/2007 6:16 PM
some tire drop data Options
Recently Visited Groups | Help | Sign in
rec.bicycles.tech Search this group Search Groups
16 messages - Collapse all
carlfo...@comcast.net View profile More options Sep 28, 4:17 pm
Some recent threads and an email today led me to measure how much a
fairly typical tire rose as I inflated it.
The results suggest that some people are fooling themselves.
First, some data from dial indicator measurements of a loaded tire's
height rise in thousandths of an inch from 40 to 130 psi, measured
from top of nominal 700x25c tire.
Tire measured 1.020" to 1.030" wide at top between 80 to 130 psi.
Total load on tire was ~85 pounds, resting on a scale, but the tire
stood on a concrete floor for the test.
inch mm inch
psi rise rise change
--- ----- ---- ------
40 0.000 0.00 n/a
50 0.021 0.53 0.021
60 0.038 0.97 0.017
70 0.052 1.32 0.014
80 0.063 1.60 0.011
90 0.076 1.93 0.013
100 0.088 2.24 0.012
110 0.100 2.54 0.012
120 0.110 2.79 0.010
130 0.120 3.05 0.010
My quick and dirty table shows only that the top of a roughly 1.020"
wide tire rose ~0.120 inches from 40 to 130 psi under an 88 pound
load.
For those interested in arbitrary figures, 15% of a tire width of
1.020" is 0.153", or 3.9 mm.
Presumably, someone could measure the diameter of a tire hanging in
mid-air and inflated to some arbitrary pressure, load it with some
weights, measure the change, and call it tire drop.
But this would require such an elaborate test rig that it would be
extremely difficult for any normal poster to even _try_ to make a
practical measurement of the difference between 90 psi and 100 psi.
After all, the difference between 90 and 100 psi with an elaborate
test rig using a dial indicator was only 0.012", about a hundredth of
an inch.
Incidentally, it is highly unlikely that pressure and a 700x25 tire's
rise have the straight linear relationship that some people suggest,
at least not over a 40 to 130 psi range with an 88 pound load.
I expect that beautifully smooth graphs of pressure and rise are just
as theoretical, oversimplified, and mistaken as similar predictions
for contact patch area, which does not follow the often-mentioned
tire-pressure/load = area prediction.
(Actual measurements of contact patches show that they fail to shrink
as much as predicted with higher pressures and fail to expand as much
Jan Heine
About this group
Subscribe to this group
This is a Usenet group - learn more
Discussions
+ new post
Sponsored Links
Bike Tires Clearance
Michelins, Continental, Tufo, More
No Sales Tax, Same Day Shipping
www.BikeTiresDirect.com
Tire Alerts - Low Prices
Keep Your Tires Inflated Correctly.
Increase efficiency, Save Gas Today
TerraPass.com
Tire Inflation
Optimizing Tire Pressure
Car Care Articles and Advice
www.autoMedia.com
See your message here...
Related Pages
Needy kids get chance to ride
Pittsburgh Tribune-Review - Dec 21, 2007
By Jessica LaDow Rich Kragness hoisted a small
Spider-Man bike onto ...
School, bicycle business create partnership focusing
on health, safety
Baltimore Sun - 15 hours ago
Northfield Elementary has joined Race Pace Bicycles
in a partnership ...
Tire fire erupts in Cumberland County
6abc.com - 8 hours ago
FAIRFIELD TOWNSHIP - December 23, 2007 --
Firefighters in Cumberland ...
Rideable Bicycle Replicas
www.hiwheel.com
Women Want Their Own Gear
New study indicates that small men's gear isn't the fit
most women ...
www.ergoweb.com
oldroads.com - Menotomy Vintage Bicycles
oldroads.com
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
2 of 13 12/23/2007 6:16 PM
as predicted with lower pressures. They stubbornly stick to a
preferred size.)
Cheers,
Carl Fogel
Reply to author Forward
Tim McNamara View profile More options Sep 28, 8:27 pm
In article <oltqf3td4ftpiiishe2kcimc8vhn5jf...@4ax.com>,
- Show quoted text -
Interesting data from Fogel Labs again; thanks, Carl. I don't have the
original article about the 15% drop figure right here to read again.
IIRC the 15% drop figure came from research by Jim Papodopolous, but
how
it was arrived at I don't know. It's a number that looks suspiciously
arbitrary (how many things in the world work out to such a nice even
number?).
Reply to author Forward
carlfo...@comcast.net View profile More options Sep 28, 9:24 pm
On Fri, 28 Sep 2007 21:27:22 -0500, Tim McNamara
- Show quoted text -
Dear Tim,
I don't know where the popular 15% figure came from or from what point
it was measured--just the weight of the front end of a bike resting on
the tire is about 10% of the typical load.
Maybe there's a clever measuring technique that was somehow confirmed
by rolling resistance tests, but it's going to have to be awfully
clever to handle differences of about a hundredth of an inch between
90 and 100 psi.
Here's a link that came in my email to a chart that graphs some kind
of 15% drop correlated with pressure for various tire sizes:
http://bp1.blogger.com/_d-Yj0VDKhWQ/RnwLUoA9sVI/AAAAAAAAAJ4/225Ym5qYK...
The graph seems to show some simple linear calculations, not actual
data points from measurements.
I suspect that actual measurements would show the straight line theory
is simply wrong.
If a tire were a piston in a car engine, then adding a 100 pound
weight (including piston) would drive a piston with an area of 1
square inch down until the pressure rose to 100 psi.
But a bicycle tire is significantly different from a metal piston in a
metal chamber.
When we load a tire, the bottom of the "piston chamber" is the
reasonably unyielding metal rim.
But on either side of the tire, the C-shaped tire walls deform outward
against the air pressure trying to keep them in their current shape
about an inch wide on a 25 mm tire, the minor axis of the toroid (your
thumb and finger going around the tire).
Meanwhile, the tire also deforms, much less against the gigantic "O"
of the tire viewed the long way around, the major axis of the toroid.
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
3 of 13 12/23/2007 6:16 PM
In effect, the tire is more like a long, narrow trampoline than the
top of a metal piston, and it distorts in a much more complicated
fashion.
This is why the simple area = load / pressure load equation fails to
predict what happens at high and low pressures for 700c x 25 tires.
The same explanation probably applies to how high a tire rises or
falls according to pressure. The sides of the tire act as scissors
jacks, applying increasing pressure at the edge of the contact patch
as pressure drops and the sides deform more and more.
As I've mentioned before, what made me suspicious of simple
straight-line predictions was knowing that a 4-inch wide trials tire
can carry a 400-pound load in a wheelstand down a paved road with only
4 psi and no way to spread out more than 4 inches. The oversimplified
equation predicts:
400 lbs / 4 (lbs/inch^2) = 100 ^ 2 = 4 x 25 inches
But a 4 x 18 trials tire is only about 26 inches in diameter, so a 25
inch long contact patch is impossible. The sidewalls had to be
exerting considerable force as springs, which seems reasonable, since
it takes considerable force to pull (or push) the wall of an inflated
tire out of shape.
Cheers,
Carl Fogel
Reply to author Forward
smokeystrodt...@gmail.com View profile More options Sep 28, 9:45 pm
On Sep 28, 9:27 pm, Tim McNamara <tim...@bitstream.net> wrote:
- Show quoted text -
Thanks for the information, Carl. I think the original article came
from Bicycling magazine. Currently you can get a version of it on the
roadbikerider.com website in the member's section.
Smokey
Reply to author Forward
Jean View profile More options Sep 29, 8:43 am
"Tim McNamara" <tim...@bitstream.net> wrote in message
news:timmcn-C026A2....@news.iphouse.com...
| In article <oltqf3td4ftpiiishe2kcimc8vhn5jf...@4ax.com>,
| carlfo...@comcast.net wrote:
|
| > Some recent threads and an email today led me to measure how much
a
| > fairly typical tire rose as I inflated it.
| >
| > The results suggest that some people are fooling themselves.
| >
....snip
|
| Interesting data from Fogel Labs again; thanks, Carl. I don't have
the
| original article about the 15% drop figure right here to read again.
| IIRC the 15% drop figure came from research by Jim Papodopolous, but
how
| it was arrived at I don't know. It's a number that looks
suspiciously
| arbitrary (how many things in the world work out to such a nice even
| number?).
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
4 of 13 12/23/2007 6:16 PM
I don't know how Berto came up with the 15% figure, but I do have a
clipping from Bicycling magazine that says "Michelin and National
recommend
selecting tire size and inflation pressure so the tire height drops by
20%
when you get on the bike". How they arrived at the 20% figure was
never
mentioned.
Reply to author Forward
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
5 of 13 12/23/2007 6:16 PM
Tim McNamara View profile More options Sep 29, 11:23 am
In article <upfrf3pifcnmdij94geh0vv2o6hi171...@4ax.com>,
- Show quoted text -
Having reviewed the article in Bicycle Quarterly ("Optimizing your
tire
pressure for your weight," BQ Vol 5, Issue 4), the 15% figure was
referenced from an article by Frank Berto (2004. Under Pressure.
Australian Cyclist March/April 2004, p. 48). I was not able to locate
the article on the Australian Cyclist Web site.
Heine measure loads on three bicycles with a rider seated on the bike
(randonneur bike, racing bike and "city" bike) and found that the
weight
distribution (% front/rear) was 45/55, 30/60 and 35/65 respectively.
Heine's article references that a 15% "tire drop" is recommended by
"several tire manufacturers." That statement is cited to Berto's
original article and no more specifics are given. The chart with the
nice linear relationships is also attributed to Berto.
> Maybe there's a clever measuring technique that was somehow confirmed
> by rolling resistance tests, but it's going to have to be awfully
> clever to handle differences of about a hundredth of an inch between
> 90 and 100 psi.
My guess would be to load the wheel through a frame or fork and
measure
the drop from the top of the tire to the ground, with an arrangement
similar to how a doctor measures your height. It would indeed need to
be carefully calibrated, perhaps some dial arrangement could be used.
> Here's a link that came in my email to a chart that graphs some kind
> of 15% drop correlated with pressure for various tire sizes:
>
http://bp1.blogger.com/_d-Yj0VDKhWQ/RnwLUoA9sVI/AAAAAAAAAJ4/225Ym5qYKT
> o/s1600- h/BQ_berto_inflationgraph.jpg
> The graph seems to show some simple linear calculations, not actual
> data points from measurements.
> I suspect that actual measurements would show the straight line
> theory is simply wrong.
That is the graph included on p 29 of BQ 5,4. It is attributed to
Berto's article in Australian Cyclist. Without being able to read the
Berto article, there isn't any way to understand how Berto came to
create that graph. I agree that such a linear relationship between
inflation and tire drop is probably unlikely, although it's
conceivable
that the relationship might be close to linear within the normal range
in inflation pressures. If you look at the Avocet rolling resistance
data, the curve of the relationship between inflation pressure and
rolling resistance flattened quite a bit at higher pressures.
Maybe you can Google up the source article by Berto, or perhaps there
is
some Australian or New Zealand or Tasmanian participant in the
newsgroup
who can provide that information.
Reply to author Forward
* * Chas View profile More options Sep 29, 12:58 pm
"Tim McNamara" <tim...@bitstream.net> wrote in message
news:timmcn-2DA059....@news.iphouse.com...
- Show quoted text -
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
6 of 13 12/23/2007 6:16 PM
Years ago I remember seeing a study that showed only a 5%-7% reduction
in
rolling resistance between 85 PSI and 110 PSI in a variety of tires.
Since most of us rode sewups in goathead country we opted to run at 85
PSI
to 90 PSI and got a lot less flats ( refer to Carl Fogel's test of
tire
puncture vs. pressure ).
Chas.
Reply to author Forward
Gary Young View profile More options Sep 29, 1:23 pm
- Show quoted text -
Jan Heine, publisher of the magazine where the graph appeared, posted
a
response on the ibob mailing list:
"The graph with the linear relationships quoted in the link below
[i.e., Carl's link, above] came from Bicycle Quarterly. It was based
on
actual measurements by Frank Berto, and his measurements did line up
roughly on a straight line (I have seen the original measurements). He
built a test rig, which he described many years ago in Bicycling
Magazine.
The graphs are extrapolated toward the ends...
The discrepancy between Carl Fogel's measurements and Frank Berto's
might be easy to explain. They measured different things. Carl
measured the rise of the tire with increasing pressure. I am not
surprised that this is not linear - the tire cannot expand
indefinitely.
Frank Berto measured how much pressure he needed for different
weights to achieve the same tire deflection of 15%. The 15% came from
tire manufacturers' recommendations. In Bicycle Quarterly's real road
tests, we found that performance decreased significantly once the
"tire drop" was more than about 13-15%. With less tire drop, higher
pressures did not yield significant performance benefits.
Please feel free to forward this clarification to rec.bike.tech.
Jan Heine
Editor
Bicycle Quarterly
140 Lakeside Ave #C
Seattle WA 98122
www.bikequarterly.com"
http://search.bikelist.org/getmsg.asp?Filename=internet-bob.10709.186...
Reply to author Forward
carlfo...@comcast.net View profile More options Sep 29, 2:24 pm
On Sat, 29 Sep 2007 12:23:39 -0500, Tim McNamara
<tim...@bitstream.net> wrote:
[snip]
>> Maybe there's a clever measuring technique that was somehow confirmed
>> by rolling resistance tests, but it's going to have to be awfully
>> clever to handle differences of about a hundredth of an inch between
>> 90 and 100 psi.
>My guess would be to load the wheel through a frame or fork and measure
>the drop from the top of the tire to the ground, with an arrangement
>similar to how a doctor measures your height. It would indeed need to
>be carefully calibrated, perhaps some dial arrangement could be used.
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
7 of 13 12/23/2007 6:16 PM
[snip]
Dear Tim,
In this case, the more careful the measurement, the sillier the
results will be. The resolution is already too fine for the subject.
There's no medical point, for example, to weighing normal adults to
within even a pound, since our weight easily varies that much
according to our last meal and visit to the bathroom. (The doctor does
not bother to have you remove your wallet, much less strip naked, when
he weighs you on his balance scales, accurate to 4 ounces.)
The "15%" tire drop figure implies resolution to at least 5%
increments, meaning that we think that 15% is what we want, not 10% or
20%.
But when compared to 10% or 20% drops, a "15% drop" means only that
somewhere between 70 and 110 psi is a good idea for tire inflation.
We hardly need elaborate charts and dial indicators to tell us that.
Here's how it works.
If a 1.000" wide tire has an absolute 15% drop of 0.150" at 90 psi
under an 85-lb load (don't ask me how to actually measure that with
repeatable accuracy), then we can apply my relative rise measurements
for a ~1" tire under the same conditions:
10 psi
theoretical measured
absolute relative
psi drop drops
--- -------- --------
x 20% 0.200" 20%
130 0.194" +0.010"
120 0.184" +0.010"
110 0.174" +0.012" \
100 0.162" +0.012" \
90 15% 0.150" 0 > 15% range
80 0.137" -0.013" /
70 0.126" -0.011" /
60 0.112" -0.014"
x 10% 0.100" 10%
50 0.091" -0.021"
Here's my test data again:
inch inch
psi rise change
--- ----- ------
40 0.000 n/a
50 0.021 0.021
60 0.038 0.017
70 0.052 0.014
80 0.063 0.011
90 0.076 0.013
100 0.088 0.012
110 0.100 0.012
120 0.110 0.010
130 0.120 0.010
In any case, inflated tires are not round to within a hundredth of an
inch. They're just slapped on aluminum rims and inflated, with the
beads creeping out roughly regularly, and then the sides bend as the
tire is loaded.
What's bending in clinchers are bias-laid plies of threads, with 66 to
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
8 of 13 12/23/2007 6:16 PM
170 threads per inch:
66 tpi 0.015"
127 tpi 0.008"
170 tpi 0.006"
A single thread is roughly as thick as a measured 10 psi difference in
tire drop.
Cheers,
Carl Fogel
Reply to author Forward
carlfo...@comcast.net View profile More options Sep 29, 2:49 pm
On Sat, 29 Sep 2007 14:23:23 -0500, Gary Young <garyyou...@gmail.com>
wrote:
- Show quoted text -
Dear Gary,
Anyone can load a tire, put a dial indicator on the top of the tire,
and measure the rise as inflation is increased in 10 psi increments.
It makes no difference whether the measurements are taken in
increasing or decreasing order.
The rise will _not_ be linear, with the effect particularly noticeable
at low pressures. If a straight line was extrapolated, that could
account for the discrepancy.
It would be fascinating to see the details of how the measurements
were achieved, since the tire deflects _most_ with the initial load.
In other words, the drop for 8 pounds of load is greatest for the
first 8 pounds (roughly the load of just a 20-lb bike on the front
tire). Measuring differences in thousandths of an inch gets awfully
tricky in practical terms out toward zero.
A 13%-15% absolute tire drop range is mentioned.
For a 1.000" tire, that's 0.130" to 0.150", a difference of 0.020".
On a ~1-inch tire, I found that a relative drop of 0.020" at ~90 psi
with an 85-lb load corresponded to a ~20 psi change in inflation.
Any bicyclist with a floor pump, a dial indicator, and some weights
can check my measurements.
You can pick up a dial indicator from Harbor Freight for about ten
bucks, less than the cost of a floor pump.
Cheers,
Carl Fogel
Reply to author Forward
* * Chas View profile More options Sep 29, 3:36 pm
"Gary Young" <garyyou...@gmail.com> wrote in message
news:U4ydnbBef9e2O2Pb...@giganews.com...
> On Fri, 28 Sep 2007 21:24:36 -0600, carlfogel wrote:
<snip>
>.....In Bicycle Quarterly's real road tests, we found that
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
9 of 13 12/23/2007 6:16 PM
> performance decreased significantly once the "tire drop" > was more than
about 13-15%. With less tire drop, higher > pressures did not yield
significant performance benefits.
Performance? Define performance. Was it an increase in rolling
resistance?
More pedal force required? Or was it anecdotal subjective opinions of
the
riders.
My personal opinion is that some riders like very hard tires and have
fooled themselves into thinking that tires run at high pressures will
MAKE
them go faster.
If I'm going to ride on a rough surface road I ride Panaracer Paselas
at
85-90PSI. If it's a smooth road surface I like Continental Grand Prixs
at
95-110 PSI. I ride sewups at 90 PSI. That's MY preference based on
ride
comfort and puncture potential.
Chas.
Reply to author Forward
carlfo...@comcast.net View profile More options Sep 29, 3:57 pm
- Show quoted text -
An email asked for details of the testing.
I wonder if other posters get as many emails as I do? Often it seems
as if people are accidentally hitting the email instead of the post
button on their newsreaders. I don't mind, but it would more fun if
they were all beautiful but lonely women.
Luckily, the test rig had been left untouched in hopes of gaining
Historic Place status, so here's a picture:
http://i24.tinypic.com/2iw4zn5.jpg
The white bathroom scales are not legal for trade, but showed ~85
pounds when shoved under the tire. They were removed for testing, lest
the tire inflation increased the contact patch area enough to cause
the scale surface to rise--remember, the measurements involved changes
as small as ten thousandths of an inch.
The yellow floor pump reads in alleged 2-lb increments. Zip ties
secure the pump head, which tended to come off during lengthy testing.
Fogel Labs has budgeted for a new O-ring.
The seat post sticks up between the jaws of the bench vise, which are
slightly open, but stop everything from toppling over. If the post had
been clamped, it might have held the front end of the bicycle down
slightly as the tire was pumped up--again, the measurements were so
tiny that such precautions were necessary.
The board was clamped to the red test frame for long-ago experiments.
Later, the weight bar was added for even stranger rituals.
The dial indicator from Sears is directly over the front axle and
contact patch. It rests on the weight bar, not the top of the tire,
partly because it was just about the right height, but mostly because
the slight expansion of the top of the tire during inflation would
have exaggerated the rise of the bottom of the tire.
A carefully machined indentation in the round weight bar assures that
the dial indicator does not slip off to the side and give false
readings. (It looks remarkably like a dent whacked with a blunt punch
and a hammer.)
The dial indicator is held by vise grips, which in turn are held in
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
10 of 13 12/23/2007 6:16 PM
place under a 10-pound weight. Vise grips were required because half
the convenient mounting lug on the back of the dial indicator was
hacksawed off in 1972 in order to fit into an awkward spot while
timing a motorcycle. I may spend ten bucks at Harbor Freight and get a
replacement, or maybe even a few bucks more for one with an adjustable
arm.
Cheers,
Carl Fogel
Reply to author Forward
anth View profile More options Sep 29, 10:42 pm
On Sat, 2007-09-29 at 12:23 -0500, Tim McNamara wrote:
> Heine measure loads on three bicycles with a rider seated on the bike
> (randonneur bike, racing bike and "city" bike) and found that the weight
> distribution (% front/rear) was 45/55, 30/60 and 35/65 respectively.
The middle figures don't add up. I'm guessing they should have been
40/60?
Reply to author Forward
Ryan Cousineau View profile More options Sep 29, 11:10 pm
In article <kddtf3drng10jfmnl02pcifrlmif8fk...@4ax.com>,
carlfo...@comcast.net wrote:
> On Sat, 29 Sep 2007 14:23:23 -0500, Gary Young <garyyou...@gmail.com>
> wrote:
> >On Fri, 28 Sep 2007 21:24:36 -0600, carlfogel wrote:
> >> On Fri, 28 Sep 2007 21:27:22 -0500, Tim McNamara
> >> <tim...@bitstream.net> wrote:
> >>>In article <oltqf3td4ftpiiishe2kcimc8vhn5jf...@4ax.com>,
> >>> carlfo...@comcast.net wrote:
[long correspondence trimmed; interested viewers are invited to check
the archives]
> Any bicyclist with a floor pump, a dial indicator, and some weights
> can check my measurements.
> You can pick up a dial indicator from Harbor Freight for about ten
> bucks, less than the cost of a floor pump.
Aha! I am on to your craven attempts to encourage the readers of rbt
to
engage in the oft-forsaken cornerstone of the Scientific Method:
reproducibility!
Well, we scholastics are on to you.
And it's a shame. I always assumed that a former literature explicator
like yourself would have had a naturally scholastic bent.
Silliness aside, I should take up your challenge, but my excuse is
that
I have too many bikes a-building right now for others.
--
Ryan Cousineau rcous...@sfu.ca http://www.wiredcola.com/
"I don't want kids who are thinking about going into mathematics
to think that they have to take drugs to succeed." -Paul Erdos
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
11 of 13 12/23/2007 6:16 PM
Reply to author Forward
carlfo...@comcast.net View profile More options Sep 29, 11:43 pm
- Show quoted text -
An odd example of measurement problems.
I took a few minutes and set up my dial calipers to hang and measure
the same tire's width as it sat in a truing stand. As I expected, the
tire widened as it was pumped up
psi width
30 0.975
40 0.985
50 0.992
60 0.996
70 0.998
80 1.007
90 1.014
100 1.018
110 1.025
120 1.029
130 1.034
140 1.040
But trying to get a good reading by rolling a dial caliper's jaws shut
on squishy rubber _felt_ a little squishy and inaccurate, even though
the results looked good.
Rather than adjusting the dial caliper to slip at less and less
resistance as its jaws closed on the rubber, I decided to try a dial
indicator, which supplies its own very gentle spring action.
Naturally, I got sidetracked and first set the dial indicator up to
measure the expansion of the top of the tire in the truing stand, not
its sideways bulge. But things turned out pretty well:
top of
psi tire
? 1.000 as low as I could get it and still feel pressure
10 0.990 probably seated a bit, moving the wrong way
20 0.994
30 0.998
40 1.002
50 1.007
60 1.011
70 1.016
80 1.023
90 1.028
100 1.033
110 1.038
120 1.042
130 1.050
140 pump head blew off
Then I set things up again in the truing stand, but turned the dial
indicator rig on the side of the tire to measure how far one side of
the tire bulged sideways as I pumped it up.
I zeroed the dial indicator, checked that everything was at right
angles, and pumped . . . Nothing.
No change at 10 psi.
I pumped to 20 psi, but still nothing happened.
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
12 of 13 12/23/2007 6:16 PM
At 30 psi, the needle still sat on 0.000.
I went up to 80 psi without any movement.
At 120 psi, there was a little movement, about 0.003 inches.
Mystified, I grabbed my dial calipers, closed their jaws on the stupid
tire, and let the air out of the dumb thing. A gratifying gap promptly
opened between the side of the tire and the jaws, so I knew that I
wasn't crazy--tires really do expand when inflated.
But another attempt with the dial _indicator_ produced the same
failure.
At first, I thought that the problem was just that the tire was
expanding outward, as well as sideways, and the dial indicator was
slipping down the side of the expanding tire, just enough for the loss
to cancel the gain.
Some of the failure was due to this movement in two directions, but I
suspect that real problem was the tiny bit of stiction in the dial
indicator rod as the rubber moved outward as well as sideways may have
made things worse, too, jamming the delicate mechanism.
Whatever the cause, the dial indicator utterly failed to measure the
sideways expansion clearly indicated by dial calipers.
Cheers,
Carl Fogel
Reply to author Forward
carlfo...@comcast.net View profile More options Sep 29, 11:55 pm
On Sun, 30 Sep 2007 05:10:12 GMT, Ryan Cousineau <rcous...@sfu.ca>
wrote:
[snip]
>Silliness aside, I should take up your challenge, but my excuse is that
>I have too many bikes a-building right now for others.
Dear Ryan,
Just remember that it could be a very bad thing if a bike with 80
pounds of weights at handlebar height topples over onto you.
Safety rope the rig to a work bench or arrange for a hefty vise's jaws
to cuddle a stout part of the bike frame.
But do _something_ to make sure that your carefully balanced test bike
rig can't fall over and hurt you.
I haven't had any accidents so far, and I don't want to read about
anyone else having different results.
Er, I mean anyone else having accidents. Different results are fine.
Cheers,
Carl Fogel
Reply to author Forward
End of messages
« Back to Discussions « Newer topic Older topic »
some tire drop data - rec.bicycles.tech | Google Groups
http://groups.google.com/group/rec.bicycles.tech/browse_thread/thread/...
13 of 13 12/23/2007 6:16 PM
Create a group - Google Groups - Google Home - Terms of Service -
Privacy Policy
©2007 Google

[Allan in Portland]

Thanks for those. I knew my numbers were a little high, but I didn't realize they were that high. I figured if people got pinch flats from our app that would be a bad thing. I also felt 

We haven't submitted the app yet, so there's still time to adjust the calculations if we wish.

-Allan

[Allan in Portland]

Thanks Wayne. I wanted to make some of my own measurements, but have been so busy creating the App in the first place, that creating a test apparatus has not remotely been in the cards.

If the App receives a strong response, that will definitely encourage us to go back and make some measurements of our own. That and we've already got a short-list of features we'd like to add.

-Allan

[Nick Bull]

There was some discussion on the randon newsgroup about this topic and I tried several different models before finding one that I thought worked "well enough".

My starting point was to develop a data set based on the "standard" tire pressure graph that's been posted in BQ -- I just put in the "optimal pressure" for each tire size at weights of 66, 77, 88, 99, 110, and 121 pounds.  The regression that worked best (adjusted R^2 of .9996) was:

 PSI = J*weight/size + K*weight/(size^2) + L*weight^2/(size) + M*weight^2/(size^2) with regression results as follows, which imply:

J=	14.63991
K=	131.8528
L=	-0.0709
M=	2.27418

Regression results follow:

Model: MODEL1 
NOTE: No intercept in model. R-square is redefined.
Dependent Variable: ZPSI       Predicted Value of PSI                 

Analysis of Variance

                         Sum of         Mean
Source          DF      Squares       Square      F Value       Prob>F

Model            4 407614.55097 101903.63774    29771.629       0.0001
Error           46    157.45082      3.42284
U Total         50 407772.00179

    Root MSE       1.85009     R-square       0.9996
    Dep Mean      84.20000     Adj R-sq       0.9996
    C.V.           2.19726

Parameter Estimates

                 Parameter      Standard    T for H0:                 Variable
Variable  DF      Estimate         Error   Parameter=0    Prob > |T|     Label

WGHTOSZ    1     14.639907    1.76404141         8.299        0.0001                                         
WGHTOSZS   1    131.852835   44.33787004         2.974        0.0047                                         
WT2OSZ     1     -0.070903    0.01489340        -4.761        0.0001                                         
WT2OSZS    1      2.274180    0.38246978         5.946        0.0001                                         

The results for each tire size & weight combo shown below compare optimal pressure from the graph (PSI) to the forecast optimal pressure (ZPSIDIR) and show the absolute percent error in ABSRERR.  The regression does a good-enough job for me for my typical weight and for the tire sizes I run.

OBS    SIZE    WEIGHT     PSI     ZPSIDIR    ABSRERR

  1     20        66      78.0     79.391    1.78281
  2     20        77      95.0     94.435    0.59453
  3     20        88     109.0    109.998    0.91537
  4     20        99     125.0    126.078    0.86261
  5     20       110     139.0    142.677    2.64513
  6     20       121     153.0    159.793    4.43997
  7     23        66      65.0     63.759    1.90962
  8     23        77      77.0     75.415    2.05792
  9     23        88      90.5     87.366    3.46255
 10     23        99     103.0     99.612    3.28959
 11     23       110     115.0    112.151    2.47705
 12     23       121     128.0    124.985    2.35515
 13     23       132     140.0    138.114    1.34731
 14     23       143     152.0    151.536    0.30496
 15     25        66      55.0     56.069    1.94368
 16     25        77      65.0     66.094    1.68253
 17     25        88      77.0     76.312    0.89288
 18     25        99      87.0     86.726    0.31547
 19     25       110      98.0     97.333    0.68079
 20     25       121     109.0    108.134    0.79418
 21     25       132     120.0    119.130    0.72494
 22     25       143     130.0    130.320    0.24617
 23     25       154     140.0    141.704    1.21729
 24     28        66      48.0     47.213    1.63881
 25     28        77      57.0     55.394    2.81687
 26     28        88      65.0     63.665    2.05451
 27     28        99      72.5     72.024    0.65665
 28     28       110      82.0     80.472    1.86284
 29     28       121      90.5     89.010    1.64621
 30     28       132      99.0     97.637    1.37670
 31     28       143     108.0    106.353    1.52488
 32     28       154     117.0    115.158    1.57404
 33     32        66      37.5     38.716    3.24169
 34     32        77      43.0     45.173    5.05259
 35     32        88      51.0     51.631    1.23694
 36     32        99      58.0     58.090    0.15572
 37     32       110      65.0     64.551    0.69069
 38     32       121      71.0     71.013    0.01835
 39     32       132      78.0     77.476    0.67147
 40     32       143      85.0     83.941    1.24619
 41     32       154      91.0     90.406    0.65224
 42     37        66      30.0     31.360    4.53302
 43     37        77      36.0     36.370    1.02914
 44     37        88      40.0     41.319    3.29836
 45     37        99      45.0     46.206    2.68103
 46     37       110      49.0     51.032    4.14663
 47     37       121      53.0     55.796    5.27453
 48     37       132      58.0     60.497    4.30590
 49     37       143      62.0     65.138    5.06066
 50     37       154      68.0     69.716    2.52362

[Allan in Portland]

On Thursday, July 5, 2012 6:10:04 PM UTC-7, Nick Bull wrote:

There was some discussion on the randon newsgroup about this topic and I tried several different models before finding one that I thought worked "well enough".

Interesting analysis. That's a whole lot more than I'd ever be able to pull-off. :-) However, I notice the errors get considerably larger with wider tires and lower weights. Unfortunately, that's exactly the area we are trying to extrapolate into.

There are two problems to solve for any Spreadsheet/Program/App/etc:
1) How best to fit the published data to a formula
2) How best to extrapolate (ie. predict) from published data to wider tires

I have a good handle on 1) because the published data was a set of lines so I've implemented a table look-up of a set of slopes & intercepts. (Of course this treats the published data as true and unassailable, but we have to start somewhere.)

In any case, if you have something you like and works for you, that's great. I won't argue anyone out of anything they've tested and know they like.

Regards,
-Allan

[Allan in Portland]

Meant to add... (argh, the google interface is such a POS.)

On Friday, July 6, 2012 9:13:10 AM UTC-7, Allan in Portland wrote:

On Thursday, July 5, 2012 6:10:04 PM UTC-7, Nick Bull wrote:

There was some discussion on the randon newsgroup about this topic and I tried several different models before finding one that I thought worked "well enough".

Interesting analysis. That's a whole lot more than I'd ever be able to pull-off. :-) However, I notice the errors get considerably larger with wider tires and lower weights. Unfortunately, that's exactly the area we are trying to extrapolate into.

There are two problems to solve for any Spreadsheet/Program/App/etc:
1) How best to fit the published data to a formula
2) How best to extrapolate (ie. predict) from published data to wider tires

I have a good handle on 1) because the published data was a set of lines so I've implemented a table look-up of a set of slopes & intercepts. (Of course this treats the published data as true and unassailable, but we have to start somewhere.)

Concerning 2), I like using ln to predict the slopes of wide tires because e is one of those constants that seems to permeate the physical world and the slopes we do have seem to fit a ln regression very well.

-Allan
 

[Nick Bull]

Yes, I agree my approach seems not to be doing as well as I'd like for the bigger tire sizes (lower weights are unfortunately not as relevant as I'd like at the moment ...).  For bigger tire sizes, more data points might be helpful to push the regression in the direction of the bigger tire sizes.  And that's where you started the whole thread, with a request for data ...

I've never been particularly enamored of "e" and "ln" in regressions -- many people use ln to detrend data, but in fact even the detrended data can still have a unit root.  Take white noise, grow it at 5 percent per year, detrend it using ln, run a regression, and you'll see that the detrended data look like they have a meaningful correlation.  But it's still just white noise!

It's still very cool that e^(i*pi)+1=0 combines some of the most deeply meaningful constants in one simple equation!

Nick

[Joe V]

Allan and Nick,

I just took a look at the data you supplied, Nick. It was good of you to supply it. So, let's assume that is the "truth" for now.

Here is the formula I derived. Nick, this is empirical, and I may be able to do better given that you used weight/size type ratios, but I'm guessing it won't do much better than this. (However, I couldn't understand why ratios with different powers as you had would make sense, so I am guessing yours is empirical as well?)

1. Rescale weight and size to weightS=(weight-100)/50 and sizeS=(size-30)/10. This is really not needed, but it makes the coefficients have more reasonable-sized values.

2. Use these coefficients in the model. (Allan, if this is not clear let me know. It's the same idea that Nick showed you.)

               Estimate

(Intercept)    5.323418

weightS        1.159610

sizeS         -1.256772

weightS^2  )  -0.186693

sizeS^2        0.319017

weightS*sizeS -0.370594

3. This gives fitted values of psi^0.4. So, to get the fitted values for psi, just take these values and raise them to the 1/0.4 power. 

The 0.4 power was not statistically different from the 0.5 power, which probably is better connected to a physical system,. but I did the fits with 0.4.

Nick, when I took your psi and fitted values and used the formula to convert them to a root mse (your Minitab o/p), I obtained 1.98 instead of the 1.85 you have on your o/p listing. Not sure why--this should not be due to round-off error. (Also, FYI, when you use Minitab and don't fit an intercept, the R^2 value is redefined, as the Minitab o/p notes. That resulting R^2 value is higher that what we normally think about as R^2, so that 0.9996 is unrealistic.)

Here are the results. First graph is your data, Nick, with one line ("connect the dots") for each tire size (sizes not shown, but are the ones you looked at and should be obvious). Note that the points are sometimes not too smoothly connected, so a smooth fit cannot (and probably should not) be perfect. 

Second graph is same as the first, but with the fits from your equation included. The third graph is the same as the first, but with the fits from the above equation used. The fourth graphs is the absolute errors (not relative errors--that is, the graph is in psi units) for the old and new fits, with an x=y line added

Allan, in case you want to use this equation, I  hope this is clear enough. If not let me know. As a check, you can use the following to verify your fits with mine.

Joe

   size weight   psi   fits sizeS weightS

1    20     66  78.0  80.05  -1.0   -0.68

2    20     77  95.0  94.02  -1.0   -0.46

3    20     88 109.0 108.60  -1.0   -0.24

4    20     99 125.0 123.64  -1.0   -0.02

5    20    110 139.0 138.99  -1.0    0.20

6    20    121 153.0 154.51  -1.0    0.42

7    23     66  65.0  64.92  -0.7   -0.68

8    23     77  77.0  76.46  -0.7   -0.46

9    23     88  90.5  88.48  -0.7   -0.24

10   23     99 103.0 100.85  -0.7   -0.02

11   23    110 115.0 113.43  -0.7    0.20

12   23    121 128.0 126.08  -0.7    0.42

13   23    132 140.0 138.68  -0.7    0.64

14   23    143 152.0 151.07  -0.7    0.86

15   25     66  55.0  56.76  -0.5   -0.68

16   25     77  65.0  66.93  -0.5   -0.46

17   25     88  77.0  77.50  -0.5   -0.24

18   25     99  87.0  88.35  -0.5   -0.02

19   25    110  98.0  99.35  -0.5    0.20

20   25    121 109.0 110.37  -0.5    0.42

21   25    132 120.0 121.28  -0.5    0.64

22   25    143 130.0 131.97  -0.5    0.86

23   25    154 140.0 142.33  -0.5    1.08

24   28     66  48.0  46.93  -0.2   -0.68

25   28     77  57.0  55.36  -0.2   -0.46

26   28     88  65.0  64.08  -0.2   -0.24

27   28     99  72.5  72.98  -0.2   -0.02

28   28    110  82.0  81.96  -0.2    0.20

29   28    121  90.5  90.88  -0.2    0.42

30   28    132  99.0  99.65  -0.2    0.64

31   28    143 108.0 108.15  -0.2    0.86

32   28    154 117.0 116.29  -0.2    1.08

33   32     66  37.5  37.46   0.2   -0.68

34   32     77  43.0  44.06   0.2   -0.46

35   32     88  51.0  50.84   0.2   -0.24

36   32     99  58.0  57.68   0.2   -0.02

37   32    110  65.0  64.50   0.2    0.20

38   32    121  71.0  71.19   0.2    0.42

39   32    132  78.0  77.67   0.2    0.64

40   32    143  85.0  83.85   0.2    0.86

41   32    154  91.0  89.64   0.2    1.08

42   37     66  30.0  30.07   0.7   -0.68

43   37     77  36.0  35.01   0.7   -0.46

44   37     88  40.0  39.99   0.7   -0.24

45   37     99  45.0  44.94   0.7   -0.02

46   37    110  49.0  49.76   0.7    0.20

47   37    121  53.0  54.38   0.7    0.42

48   37    132  58.0  58.73   0.7    0.64

49   37    143  62.0  62.74   0.7    0.86

50   37    154  68.0  66.34   0.7    1.08

[Nick Bull]

Thanks, Joe,

The original data were just my best effort to capture some x,y pairs from the graph that is taken from Berto's findings--though it would be interesting to see what that graph truly looks like when it is the original data complete with measurement error.  So ... given the amount of uncertainty there, it seemed like once I had a regression that kind of worked, it was time to stop.  It's just for figuring out what to pump my tires up to!  Step one in the process is knowing how much I and my bike and equipment weigh, plus the weight distribution between wheels, all of which is usually somewhat uncertain, as is the actual size of my tires. And when I pump my tires, I'm using an analog gauge, so it's just approximate, and when I take the hose off the valve stem some unknown quantity of air escapes, adding to the uncertainty.  And it seems like a wide range of pressures all feels not too wildly different when I'm on the bike.  Though the other day, riding to work it felt like I was working extremely hard and my legs were really hurting but just not getting the expected speed.  Turns out my tires were about 30 pounds low!

Anyway, I think your regression probably looks like it's doing a better job!

Nick 

[Allan in Portland]

Um, wow. That's some strong medicine. So you're saying the equation is:

PSI = [ 1.159610 * ((load - 100)/50)      +

          -0.186693 * ((load - 100)/50)^2   +

          -1.256772 * ((width - 30)/10)      +

           0.319017 * ((width - 30)/10)^2   +

           -0.370594 * ((load - 100)/50) * ((width - 30)/10) ]^0.4

How did you get (load-50)/100 & (width-30)/10? That seems almost totally random.

I take it multiplying the load & width there at the end is a normal statistical regression thing to do?

Oh, and width is mm and load is kg?

Thanks,

-Allan

[Joe V]

Allan,

What you said is correct, except that weight is in pounds (I just used the data that Nick supplied).

I took, for example, load - 100 because the average load was about 100. I divided by 50 because the range of loads was in that ballpark. You are correct that those numbers are arbitrary. I did that to make the coefficients have a reasonable size--here they turned out to be in range of 0.2 to 1.3 aside from their signs.

If I used other constants, or just used load instead of (load - 100)/50, the coefficients would change but the the PSI answers would be the same. (This is because I used a polynomial of degree 2, if that means anything to you. That polynomial includes that weight*size feature--yes, that is a standard thing to do, and helps the model fit better--at least this one.) 

If I had used load and weight directly, here are what the coefficients would be:

              Estimate

(Intercept)  6.675e+00

weight       6.036e-02

size        -2.430e-01

weight^2      -7.468e-05

size^2       3.190e-03

weight:size -7.412e-04

so the weight coefficient would be -0.00007468. Ugly, and with only 4 digits (at least for the default o/p here) instead of the 6 you see below.

Joe